Capitolo 28 Modello di regressione in un’ottica Bayesiana
Seguirò qui l’approccio di McElreath (2020) per riproporre i temi precedenti, relativi all’analisi di regressione, adottando un punto di vista Bayesiano. In generale possiamo dire che il problema è quello di descrivere, mediante un modello statistico, il modo in cui una variabile, chiamata variabile dipendente, è associata a qualche altra variabile, chiamata variabile indipendente. Se la variabile indipendente è statisticamente associata con la variabile dipendente, allora possiamo usarla per prevedere il valore della variabile dipendente.
Per fare un esempio, userò qui i dati del primo parziale di Psicometria dell’AA 2020/2021. C’erano 30 quiz e a ciascuno gli studenti potevano dare una risposta corretta (codificata con 1) oppure no. In questo esempio ho considerato le risposte non date come risposte non corrette (codificate con 0).
Come variabile dipendente userò una misura di prestazione nel compito. La misura più ovvia è il punteggio totale (la somma delle riposte corrette). Qui ho usato un indice migliore, ovvero il livello di abilità di ciascun rispondente calcolato con il modello di Rasch. È una misura simile al punteggio totale, ma meno rumorosa. L’ho chiamata theta.
Come variabile indipendente userò il tempo di consegna del compito. Sembra infatti sensato chiedersi se, conscendo il tempo impiegato per completare il compito, sia possibile prevedere il voto all’esame. Per facilitare l’interpretazione ho trasformato il tempo di consegna (in minuti) dividendolo per 6. In questa nuova scala, dunque, l’unità di misura (il valore 1) corrisponde a 10 minuti.
Carico i pacchetti che mi servono:
suppressPackageStartupMessages(library("here"))
suppressPackageStartupMessages(library("tidyverse"))
suppressPackageStartupMessages(library("skimr"))
suppressPackageStartupMessages(library("rethinking"))
options(show.signif.stars = FALSE)Leggo i dati:
Anche se quella considerata qui non è una domanda scientifica molto interessante, la mia motivazione è quella di descrivere il meccanismo della stima Bayesiana dell’associazione tra due variabili.
Uso la funzione precis() del pacchetto rethinking per dare un’occhiata ai dati:
rethinking::precis(dat)
#> mean sd 5.5% 94.5% histogram
#> is_female 7.165775e-01 0.4518695 0.000000 1.0000000 ▂▁▁▁▁▁▁▁▁▇
#> theta 3.781598e-02 1.3522999 -1.665091 2.4576095 ▁▁▁▃▇▇▂▁▁▁
#> tot_score 6.087344e-01 0.2029378 0.300000 0.9333333 ▁▁▂▅▅▇▇▇▃▂
#> t 7.400535e+01 7.6210640 60.000000 79.0000000 ▁▁▁▁▁▁▁▁▂▇
#> time 1.233422e+01 1.2701773 10.000000 13.1666667 ▁▁▁▁▁▁▂▇▃
#> proficiency -8.208280e-17 1.0000000 -1.259267 1.7893911 ▁▁▁▁▂▇▇▅▃▂▁▁▁▁Esamino più in dettaglio la variabile theta (l’abilità degli studenti):
summary(dat$theta)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> -4.08875 -0.81942 -0.16520 0.03782 0.78657 4.48244Creo un diagramma a dispersione:
plot(
jitter(dat$time),
jitter(dat$theta),
xlab = "Tempo di completamento (in unità di 10 minuti)",
ylab = "Abilità",
main = "Psicometria: primo parziale AA 2020/2021"
)
abline(lm(theta ~ time, data = dat))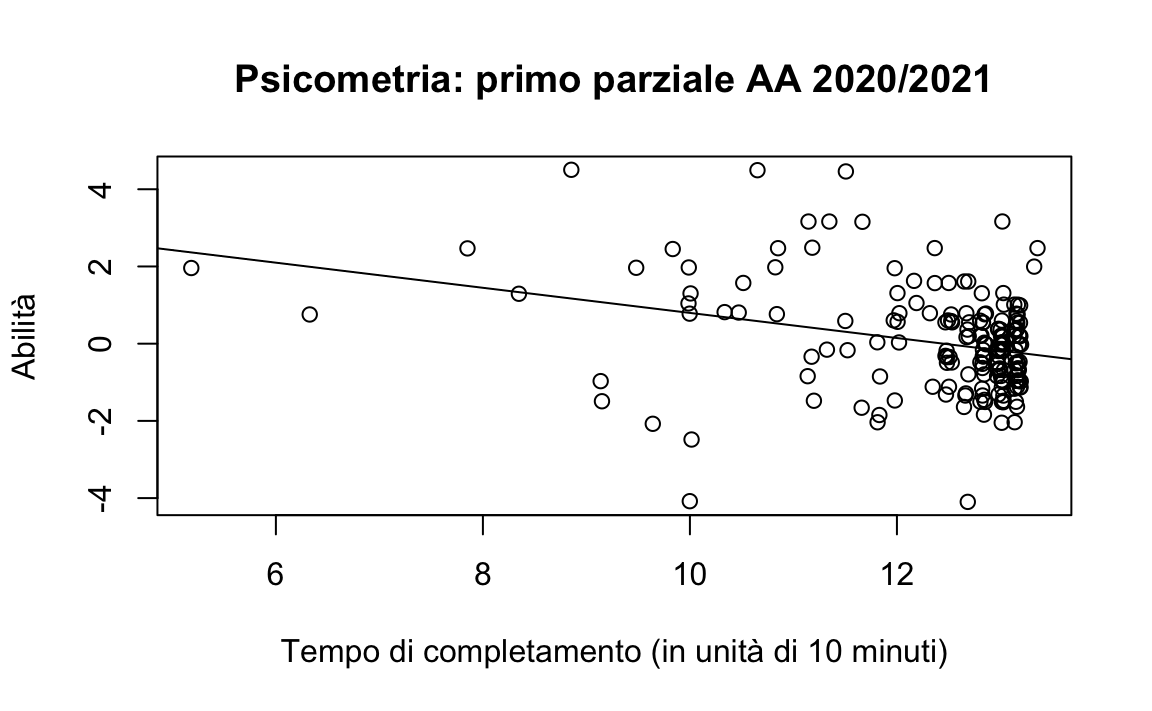 Il diagramma a dispersione indica che i dati sono molto rumorosi. Sembra però esserci una relazione tra le due varibili: a tempi di consegna maggiori sono associali livelli più bassi dell’abilità dei rispondenti. Guardando il grafico possiamo dunque pensare che la conoscenza del tempo di consegna possa contribuire alla predizione del livello di abilità degli studenti.
Il diagramma a dispersione indica che i dati sono molto rumorosi. Sembra però esserci una relazione tra le due varibili: a tempi di consegna maggiori sono associali livelli più bassi dell’abilità dei rispondenti. Guardando il grafico possiamo dunque pensare che la conoscenza del tempo di consegna possa contribuire alla predizione del livello di abilità degli studenti.Poniamoci dunque il problema di utilizzare il meccanismo dell’aggiornamento Bayesiano per descrivere l’associazione tra queste due variabili. Iniziamo in un modo semplice e poniamoci semplicemente il problema di implementare il meccanismo dell’aggiornamento Bayesiano nel quale combiniamo una distribuzione a priori per un parametro con la verosimiglianza, così da ottenere la distribuzione a posteriori. Applichiamo dunque l’aggiornamento Bayesiano alla nostra variabile dipendente: theta.
Posso descrivere il meccanismo dell’aggiornamento Bayesiano per la variabile theta nel modo seguente:
\[ \text{proficiency} \sim N(\mu, \sigma)\\ \mu \sim N(0, 2.5)\\ \sigma \sim Unif(0, 5) \] La verosimiglianza ci dice che \(\theta\) si distribuisce in maniera Normale. La distribuzione a priori per il parametro \(\mu\) è centrata sullo 0 con una deviazione standard sufficiente da coprire tutta la gamma possibile di valori osservati.
Per \(\sigma\) ho scelto unba distribuzione a priori piuttosto grande, alla luce delle informazioni fornite dal campione:
sd(dat$theta)
#> [1] 1.3523Utilizzo ora la sintassi di rethinking per specificare l’aggiornamento Bayesiano:
Adatto il modello ai dati usando l’approssimazione quadratica per calcolare la distribuzione a posteriori:
m <- quap(flist, data = dat)Posso riassumere la distribuzione a posteriori con la funzione precis():
precis(m, prob = 0.95)
#> mean sd 2.5% 97.5%
#> mu 0.03775628 0.09854847 -0.1553952 0.2309077
#> sigma 1.34867829 0.06973824 1.2119938 1.4853627Questi numeri forniscono i risultati dell’approssimazione quadratica per la distribuzione marginale a posteriori di ciascun parametro. Ciò significa che i valori più plausibile a posteriori per \(\mu\), alla luce dei dati e considerata la distribuzione a priori che è stata specificata, è data da una distribuzione gaussiana con media 0.04 e deviazione standard 0.10. Per il parametro \(\mu\) abbiamo anche l’intervallo di credibilità al 95%. Il valore assoluto di questi numeri non ha molta importanza, in quanto tali valori andrebbero confrontati con il livello di difficoltà degli item del quiz, nel contesto della teoria dei modelli di risposta agli item – ma questo non è lo scopo della discussione presente. Lo scopo è quello di implementare l’aggiornamento Bayesiano utilizzando le funzioni di rethinking e le istruzioni R precedenti mostrano come possiamo ottenere questo risultato.
28.1 Predizione lineare
Quello che abbiamo fatto finora è stato specificare un modello statistico Normale per la distribuzione dei valori di abilità degli studenti di Psicometria. Ora ci porremo il problema di cercare di predire il livello di abilità degli studenti usando il tempo di consegna del primo paziale di Psicometria. Come facciamo ad introdurre un predittore della nostra variabile dipendente (l’abilità, ovvero \(\theta\)) nel modello statistico che abbiamo specificato in precedenza?
La rispsta alla domanda precedente si ottiene specificando la media \(\mu\) della distribuzione Normale come funzione lineare del predittore di interesse, ovvero time (il tempo che è stato necessario per completare la prova). Ovvero,
\[ \mu = E(\theta) = a + b \times \text{time}. \] Quello che farà l’aggiornamento Bayesiano sarà di calcolare la distribuzione a posteriori di questa combinazione lineare. Ovvero, prenderà un campione casuale dalla distribuzione a posteriori ottenuta esaminando tutti i possibili valori dei parametri \(a\) e \(b\), e pesando la plausibilità dei valori possibili dei parametri mediante la logica dell’aggiornamento Bayesiano. In altri termini, l’aggiornamento Bayesiano si chiede: “considera tutte le rette possili che descrivono l’associazione tra abilità e tempo di consegna e poi ordina tali rette di regression in funzione della loro plausibilità, alla luce dei dati.” La risposta che otteniamo sono le distribuzioni a posteriori dei parametri \(a\) e \(b\) che individuano la retta che meglio descrive l’associazione tra abilità e tempo di consegna, alla luce dei dati e delle distribuzioni a priori dei parametri che sono state scelte.
Possiamo scrivere il modello di regressione in questo modo:
flist <- alist(
theta ~ dnorm(mu, sigma),
mu <- a + b * time,
a ~ dnorm(0, 10),
b ~ dnorm(0, 10),
sigma ~ dunif(0, 10)
)La verosimiglianza è specificata come abbiamo fatto in precedenza: diciamo che l’abilità di ciascun rispondente è un’osservazione che proviene da una distribuzione Normale di parametri \(\mu\) e \(\sigma\).
La novità è che il valore atteso di tale distribuzione Normale non è più costante, com’era in precedenza, ma è deterministicamente associato ad un’altra variabile, ovvero time. Questo significa che, per il modello che specifichiamo, al variare di time varia anche il valore atteso di theta. E questa relazione non ha nulla di aleatorio: è una relazione deterministica. Geometricamente, è una retta.
L’equazione di una retta dipende da due parametri, \(a\) e \(b\). Quindi dobbiamo specificare le distribuzioni a priori per i valori possibili di questi parametri. Dico che dobbiamo specificare le distribuzioni a priori per questi parametri perché questi sono i parametri che non conosciamo, sono i parametri che vogliamo trovare, perché sono quelli che descrivono la relazione tra le variabili di interesse, theta e time. Ci chiediamo quali sono i parametri della retta che meglio predice theta conoscendo time.
Come facciamo a determinare la distribuzione a priori per \(a\) e \(b\)? È possibile usare strategie diverse. Qui uso delle distribuzioni a priori “vagamente informative.” Ovvero, distribuzioni a priori che includano i valori possibili del parametro, ma tali per cui non forzeranno la distribuzione a posteriori in una direzione o un’altra. Sono distribuzioni a priori “deboli,” che hanno una scarsissima influenza sulla distribuzione a posteriori. Assomigliano a distribuzioni uniformi, con l’unica differenza che escludono i valori veramente “impossibili” dei parametri.
Adatto dunque il modello così costruito ai dati osservati:
m1 <- quap(
flist,
data = dat
)Estraggo un campione casuale dalla distribuzione a posteriori:
post <- extract.samples(m1)
post[1:5, ]
#> a b sigma
#> 1 3.655263 -0.3015319 1.208449
#> 2 3.266525 -0.2532797 1.290998
#> 3 3.490181 -0.2712000 1.275523
#> 4 5.633546 -0.4518713 1.269671
#> 5 4.141387 -0.3274958 1.296369Produco una rappresentazione grafica della distribuzione a posteriori per i tre parametri:
par(mfrow = c(1, 3))
dens(
post$a, lwd = 2.5, xlab = "",
ylab = "Densità", main = "p(a | x, y)",
cex.lab = 1.5, cex.axis = 1.35, cex.main = 1.5,
cex.sub = 1.5
)
dens(
post$b, lwd = 2.5, xlab = "",
ylab = "", main = "p(b | x, y)",
cex.lab = 1.5, cex.axis = 1.35, cex.main = 1.5,
cex.sub = 1.5
)
dens(
post$sigma, lwd = 2.5, xlab = "",
ylab = "", main = "p(sigma | x, y)",
cex.lab = 1.5, cex.axis = 1.35, cex.main = 1.5,
cex.sub = 1.5
)
par(mfrow = c(1, 1))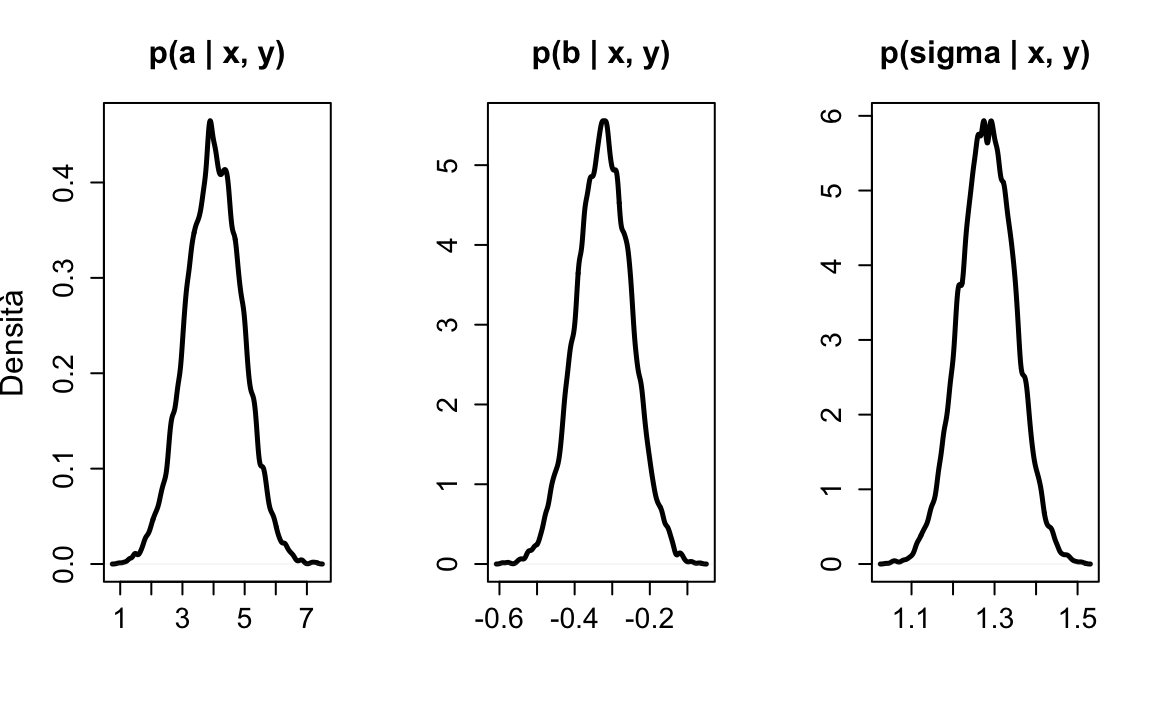 Riassumo la distribuzione a posteriori di ciascun parametro con l’intervallo di credibilità al 95%:
Riassumo la distribuzione a posteriori di ciascun parametro con l’intervallo di credibilità al 95%:
precis(m1, prob = 0.95)
#> mean sd 2.5% 97.5%
#> a 4.0192583 0.91521934 2.2254613 5.8130552
#> b -0.3228243 0.07381656 -0.4675021 -0.1781465
#> sigma 1.2840762 0.06639838 1.1539377 1.4142146Adesso rifaccio la stessa analisi utilizzando l’approccio frequentista, ovvero usando solo la verosimiglianza e ignorando le distribuzioni a priori. Dato che le distribuzioni a priori per i parametri sono debolmente informative, non mi aspetto grandi differenze rispetto ai risultati precedenti.
La soluzione che utilizza solo la verosimiglianza, ovvero la soluzione di massima verosimiglianza, si ottiene con la funzione lm():
fm <- lm(theta ~ time, dat)
summary(fm)
#>
#> Call:
#> lm(formula = theta ~ time, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.8865 -0.7484 0.0137 0.6409 4.1730
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 4.05353 0.92405 4.387 1.93e-05
#> time -0.32557 0.07453 -4.369 2.08e-05
#>
#> Residual standard error: 1.291 on 185 degrees of freedom
#> Multiple R-squared: 0.09352, Adjusted R-squared: 0.08862
#> F-statistic: 19.09 on 1 and 185 DF, p-value: 2.08e-05Il risultato è conforme alle nostre aspettative: i due approcci producono valori quasi identici per i parametri \(a\), \(b\) e \(\widehat{sigma}\).
Il parametro \(b\) ci dice che, all’aumentare di un’unità di tempo (qui, 10 minuti), il valore atteso dell’abilità dello studente diminuisce di -0.32 punti.
La deviazione standard dell’abilità è
sd(dat$theta)
#> [1] 1.3523Per dare un significato a \(b\) possiamo dire che è pari a
0.32557 / 1.3523
#> [1] 0.2407528circa un quarto di deviazione standard della distribuzione dei punteggi di abilità.
La gamma di variazione della variabile tempo di consegna è
Quindi, la variazione attesa del punteggio di abilità, in base alla predizione derivante dal tempo di consegna è pari a
0.32557 * 8.166667
#> [1] 2.658822Considerato che la gamma di variazione dell’abilità è
questo significa che la capacità predittiva del tempo di consegna è ben altro che trascurabile. Questo è illustrato nel grafico seguente.
plot(
jitter(dat$time),
jitter(dat$theta),
xlab = "Tempo di completamento (in unità di 10 minuti)",
ylab = "Abilità",
main = "Psicometria: primo parziale AA 2020/2021"
)
abline(fm)
fit_val <- function(a, b, x) {
a + b * x
}
arrows(6, fit_val(coef(fm)[1], coef(fm)[2], 8),
8, fit_val(coef(fm)[1], coef(fm)[2], 8),
length = 0.1)
arrows(6, fit_val(coef(fm)[1], coef(fm)[2], 6),
6, fit_val(coef(fm)[1], coef(fm)[2], 8),
length = 0.1)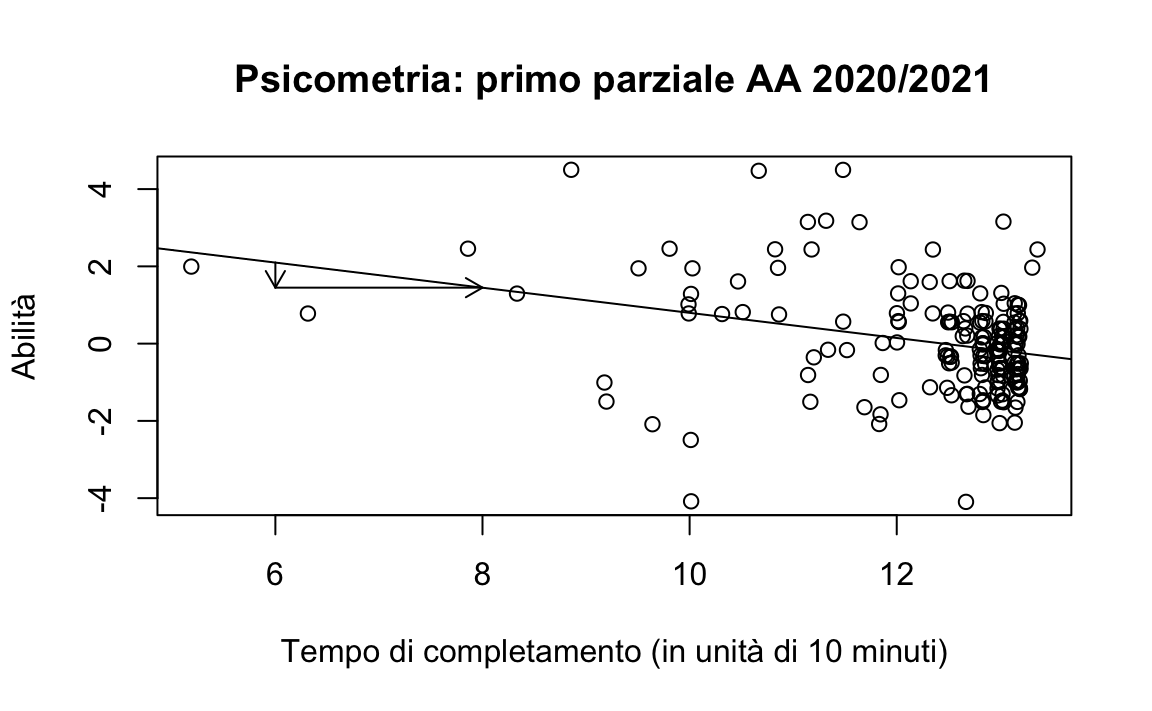
Nel modello statistico precedente, il coefficiente \(a\) è di scarso interesse: ci dice qual è il valore atteso dell’abilità per tempi di consegna pari a zero – ovviamente una situazione implausibile.
Possiamo migliorare il modello statistico nel modo seguente. Possiamo “centrare” il predittore, ovvero esprimerlo come differenze rispetto alla media. Che conseguenza avrà questa trasformazione dei dati sul coefficiente \(b\)? Ovviamente nessuna, perché ci siamo limitati a traslare rigidamente la nube di punti nel diagramma a dispersione in modo tale che la media della variabile sull’asse \(x\) diventi uguale a zero. Dato che la trasformazione dei dati corrisponde ad una traslazione rigida della nube di punti, la pendenza della retta di regressione non cambierà.
Invece cambierà l’intercetta. Dopo avere centrato la variabile \(x\), l’intercetta corrisponderà al valore atteso della variabile dipendente in corrispondenza della media del predittore. Questa è un’informazione a cui possiamo essere interessati e quindi assegna un senso al coefficiente \(a\). Questa interpretazione è possibile perché la retta di regressione (dei minimi quadrati) passa per il punto \((\bar{x}, \bar{y})\). Se la retta di regressione passa per il punto indicato, ne segue che il parametro \(a\) avrà l’interpretazione fornita sopra.
Calcolo la media di time:
dat$time_bar <- mean(dat$time)Il modello statistico diventa:
formula <- alist(
theta ~ dnorm(mu, sigma),
mu <- a + b * (time - time_bar),
a ~ dnorm(0, 10),
b ~ dnorm(0, 10),
sigma ~ dunif(0, 10)
)Adatto il modello ai dati:
m1 <- quap(
formula,
data = dat
)Esamino la distribuzione a posteriori:
precis(m1, prob = 0.95)
#> mean sd 2.5% 97.5%
#> a 0.03781275 0.09389640 -0.1462208 0.2218463
#> b -0.32555683 0.07412354 -0.4708363 -0.1802774
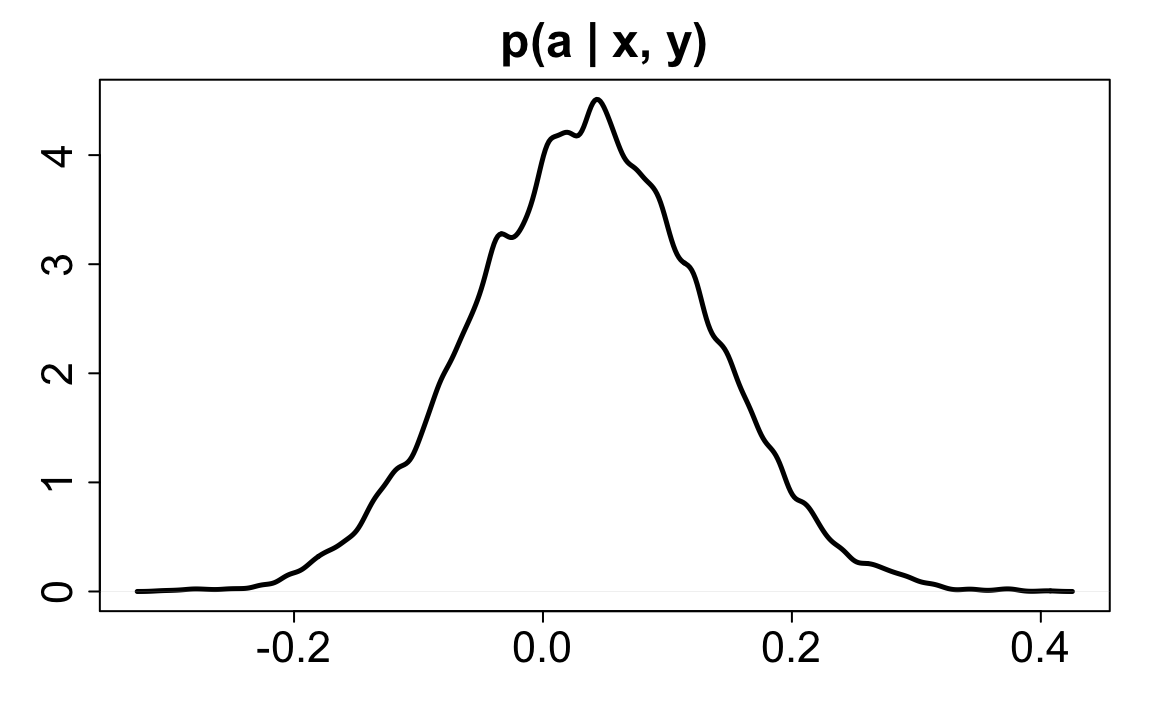
#> sigma 1.28407056 0.06639754 1.1539338 1.4142073Ora il parametro \(a\) è pari a 0.04. Questo è il valore atteso dell’abiltà per un tempo di consegna medio.
Qui di seguito è presentata una rappresentazione grafica della distribuzione a posteriori di \(a\):
post <- extract.samples(m1)
dens(
post$a, lwd = 2.5, xlab = "",
ylab = "", main = "p(a | x, y)",
cex.lab = 1.5, cex.axis = 1.35, cex.main = 1.5,
cex.sub = 1.5
)
28.2 Confronto tra inferenza Bayesiana e frequentista
Ritorniamo a \(b\) e poniamoci il problema dell’inferenza. La risposta Bayesiana è data dall’intervallo di credibilità. Nel caso di \(b\) abbiamo l’intervallo [-0.47, -0.18]. Calcoliamo l’intervallo di fiducia frequentista. Per fare questo usiamo la stima di massima verosimiglianza dei parametri:
fm <- lm(theta ~ time, data = dat)
summary(fm)
#>
#> Call:
#> lm(formula = theta ~ time, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.8865 -0.7484 0.0137 0.6409 4.1730
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 4.05353 0.92405 4.387 1.93e-05
#> time -0.32557 0.07453 -4.369 2.08e-05
#>
#> Residual standard error: 1.291 on 185 degrees of freedom
#> Multiple R-squared: 0.09352, Adjusted R-squared: 0.08862
#> F-statistic: 19.09 on 1 and 185 DF, p-value: 2.08e-05L’intervallo di fiducia è
quasi identico a quello Bayesiano. Di nuovo, questa è una conseguenza dell’avere usato distribuzioni a priori debolmente informative.
Dall’output della funzione lm() vediamo anche che l’indice di determinazione è pari a 0.09: il 9% della varianza dei punteggi di abilità è spiegato dalla variazione del tempo di consegna. È possibile calcolare anche l’equivalente Bayesiano di tale indice. Ma non è facile farlo con le funzioni di rethinking, per cui non lo discuteremo qui. Per l’esempio presente, non mi aspetto che sia molto diverso da 0.09.
In termini frequentisti, il valore di 0.09 è stato calcolato nel modo seguente:
sum((fm$fitted.values - mean(dat$theta))^2) / sum((dat$theta - mean(dat$theta))^2)
#> [1] 0.09351571Questa è la prima misura di bontà di adattamento del modello lineare ai dati. Ma ne abbiamo una seconda, ovvero l’errore standard della regressione. Nei termini dell’analisi frequentista, la stima dell’errore standard della regressione è uguale a 1.291. Questo valore è quasi identico alla stima Bayesiana del parametro sigma (1.28), che dunque ha la stessa interpretazione: esso corrisponde circa alla grandezza del residuo medio:
Possiamo dunque dire che, usando la retta di regressione, compiamo in media un errore pari a 1.28 nel predire l’abilità \(\theta\) conoscendo il tempo di consegna.
28.3 Confronti tra medie
I confronti tra le medie dei gruppi possono essere pensati come casi particolari della regressione lineare. A questo scopo dobbiamo usare delle variabili dummy (che assumono solo i valori 0 e 1) nel modello. Per l’esempio che stiamo discutendo, una variabile dummy è is_female. Tale variabile ha valore 1 per le femmine e 0 per i maschi. Possiamo dunque usare questa variabile per chiederci se la media dell’abilità delle femmine sia diversa da quella dei maschi.
Nel campione esaminato ci sono
table(dat$is_female)
#>
#> 0 1
#> 53 134134 femmine e 53 maschi.
Calcolo l’abilità media per i due gruppi:
dat %>%
group_by(is_female) %>%
summarise(
avg_prof = mean(theta, na.rm = TRUE),
stderr = sqrt(var(theta, na.rm = TRUE) / n())
)
#> # A tibble: 2 x 3
#> is_female avg_prof stderr
#> <int> <dbl> <dbl>
#> 1 0 -0.0162 0.180
#> 2 1 0.0592 0.119Le femmine hanno un livello di abilità maggiore di quello dei maschi. È questa una differenza robusta o possiamo attribuirla semplicemente alla variabilità campionaria?
Inizio qui ad usare l’approccio di massima verosimiglianza per eseguire l’analisi di regressione e per interpretare i coefficienti del modello con riferimento alle medie dei gruppi.
fm1 <- lm(theta ~ is_female, data = dat)
summary(fm1)
#>
#> Call:
#> lm(formula = theta ~ is_female, data = dat)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.1479 -0.8786 -0.1490 0.7274 4.4987
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -0.01624 0.18619 -0.087 0.931
#> is_female 0.07544 0.21996 0.343 0.732
#>
#> Residual standard error: 1.356 on 185 degrees of freedom
#> Multiple R-squared: 0.0006354, Adjusted R-squared: -0.004767
#> F-statistic: 0.1176 on 1 and 185 DF, p-value: 0.732Dai risultati forniti da lm() possiamo vedere che il valore dell’intercetta
fm1$coefficients[1]
#> (Intercept)
#> -0.01624243corrisponde alla media del gruppo codificato con 0
mean(dat[dat$is_female == 0, ]$theta)
#> [1] -0.01624243Inoltre, possiamo vedere che il coefficiente \(b\)
fm1$coefficients[2]
#> is_female
#> 0.07543971è uguale alla differenza tra la media del gruppo codificato con 0 e la media del gruppo codificato con 1, ovvero è uguale alla differenza tra le medie dei due gruppi:
-0.01624243 - 0.05919728
#> [1] -0.07543971Dunque, il test frequentista dell’ipotesi nulla \(\beta = 0\) nel modello di regressione è equivalente al test t di Student per due gruppi indipendenti:
t.test(theta ~ is_female, data = dat, var.equal = TRUE)
#>
#> Two Sample t-test
#>
#> data: theta by is_female
#> t = -0.34298, df = 185, p-value = 0.732
#> alternative hypothesis: true difference in means is not equal to 0
#> 95 percent confidence interval:
#> -0.5093846 0.3585051
#> sample estimates:
#> mean in group 0 mean in group 1
#> -0.01624243 0.05919728I risultati sono identici a quelli trovati con l’analisi di regressione.
Usiamo ora l’approccio Bayesiano:
flist2 <- alist(
theta ~ dnorm(mu, sigma),
mu ~ a + b * is_female,
a ~ dnorm(0, 5),
b ~ dnorm(0, 5),
sigma ~ dunif(0, 5)
)Adatto il modello:
m2 <- quap(
flist2,
data = dat
)Esamino la distribuzione a posteriori
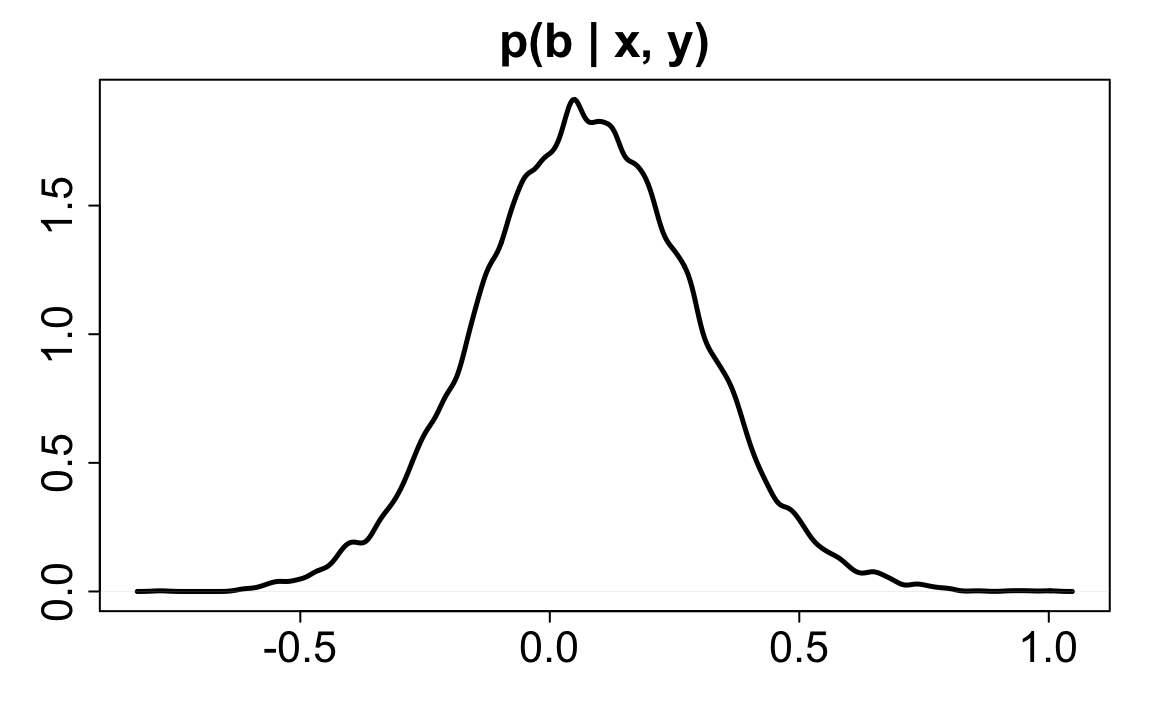
post2 <- extract.samples(m2)
dens(
post2$b, lwd = 2.5, xlab = "",
ylab = "", main = "p(b | x, y)",
cex.lab = 1.5, cex.axis = 1.35, cex.main = 1.5,
cex.sub = 1.5
)
precis(post2, prob = 0.95)
#> mean sd 2.5% 97.5% histogram
#> a -0.01644598 0.18445147 -0.3828843 0.3417742 ▁▁▂▇▇▂▁▁
#> b 0.07585907 0.21640483 -0.3456973 0.5051490 ▁▁▂▅▇▅▁▁▁▁
#> sigma 1.34820547 0.07064526 1.2073835 1.4847704 ▁▁▁▂▅▇▇▅▂▁▁▁Possiamo confrontare l’intervallo di credibilità al 95% con l’intervallo di fiducia frequentista fornito dalla funzione t.test(). Vediamo che sono quasi identici (a parte il segno invertito, che signifca che la differenza tra le medie dei due gruppi è stata fatta come \(\bar{Y_2} - \bar{Y_1}\) anziché come \(\bar{Y_1} - \bar{Y_2}\)). I risultati dunque non consentono di affermare che le abilità medie delle femmine differiscono da quelle dei maschi, rispetto alla conoscenza degli argomenti del programma d’esame di Psicometria.