Capitolo 18 Funzioni di densità di probabilità
In precedenza abbiamo esaminato la distribuzione di massa di probabilità di una variabile aleatoria discreta, ovvero la distribuzione Binomiale. Prenderemo ora in esame le densità di probabilità di alcune variabili aleatorie continue. La più importante di esse è la distribuzione Normale. In realtà vedremo che non c’è solo una distribuzione Normale, ma ce ne sono molte. Tali distribuzioni sono anche dette Gaussiane in onore di Carl Friedrich Gauss (uno dei più grandi matematici della storia il quale, tra le altre cose, scoprì l’utilità di tale funzione di densità per descrivere gli errori delle osservazioni astronomiche). Adolphe Quetelet, il padre delle scienze sociali quantitative, fu il primo ad applicare tale densità alle misurazioni dell’uomo. Karl Pearson usò per primo il termine “distribuzione Normale” anche se ammise che questa espressione “ha lo svantaggio di indurre le persone a credere che tutte le altre distribuzioni di frequenza siano in un senso o nell’altro anormali.”
18.1 Distribuzione Normale
Chi preferisce un approccio grafico, può consultare il link. Dopo le vignette, per introdurre le distribuzioni normali, considereremo un esempio proposto da (McElreath, 2020).
Supponiamo che vi siano mille persone tutte allineate su una linea di partenza. Quando viene dato un segnale, ciascuna persona lancia una moneta e fa un passo in una direzione oppure nella direzione opposta a seconda che sia uscita testa o croce. Supponiamo che la lunghezza di ciascun passo vari da 0 a 1 metro. Ciascuna persona lancia la moneta 16 volte e dunque fa 16 passi.
Alla conclusione di queste passeggiate aleatorie (random walk), non possiamo sapere dove si troverà ciascuna delle persone considerate, ma possiamo conoscere con certezza le caratteristiche della distribuzione delle mille distanze dall’origine. Per esempio, possiamo predire la proporzione di persone che si saranno spostate avanti oppure indietro. Oppure, possiamo predire la proporzione di persone che si troveranno ad una certa distanza dalla linea di partenza (es., 1.5 m).
Queste predizioni sono possibili perché le distanze create in questo modo si distribuiscono secondo la legge Normale. È facile simulare questo processo usando R. I risultati della simulazione sono riportati qui di seguito.
set.seed(4)
pos <-
replicate(100, runif(16, -1, 1)) %>% # here's the simulation
as_tibble() %>% # for data manipulation, we'll make this a tibble
rbind(0, .) %>% # here we add a row of zeros above the simulation results
mutate(step = 0:16) %>% # this adds a step index
gather(key, value, -step) %>% # here we convert the data to the long format
mutate(person = rep(1:100, each = 17)) %>% # this adds a person id index
# the next two lines allow us to make cumulative sums within each person
group_by(person) %>%
mutate(position = cumsum(value)) %>%
ungroup() # ungrouping allows for further data manipulation
ggplot(data = pos,
aes(x = step, y = position, group = person)) +
geom_vline(xintercept = c(4, 8, 16), linetype = 2) +
geom_line(aes(color = person < 2, alpha = person < 2)) +
scale_color_manual(values = c("skyblue4", "black")) +
scale_alpha_manual(values = c(1/5, 1)) +
scale_x_continuous("Numero di passi", breaks = c(0, 4, 8, 12, 16)) +
labs(
y = "Posizione"
)
theme(legend.position = "none")
#> List of 1
#> $ legend.position: chr "none"
#> - attr(*, "class")= chr [1:2] "theme" "gg"
#> - attr(*, "complete")= logi FALSE
#> - attr(*, "validate")= logi TRUE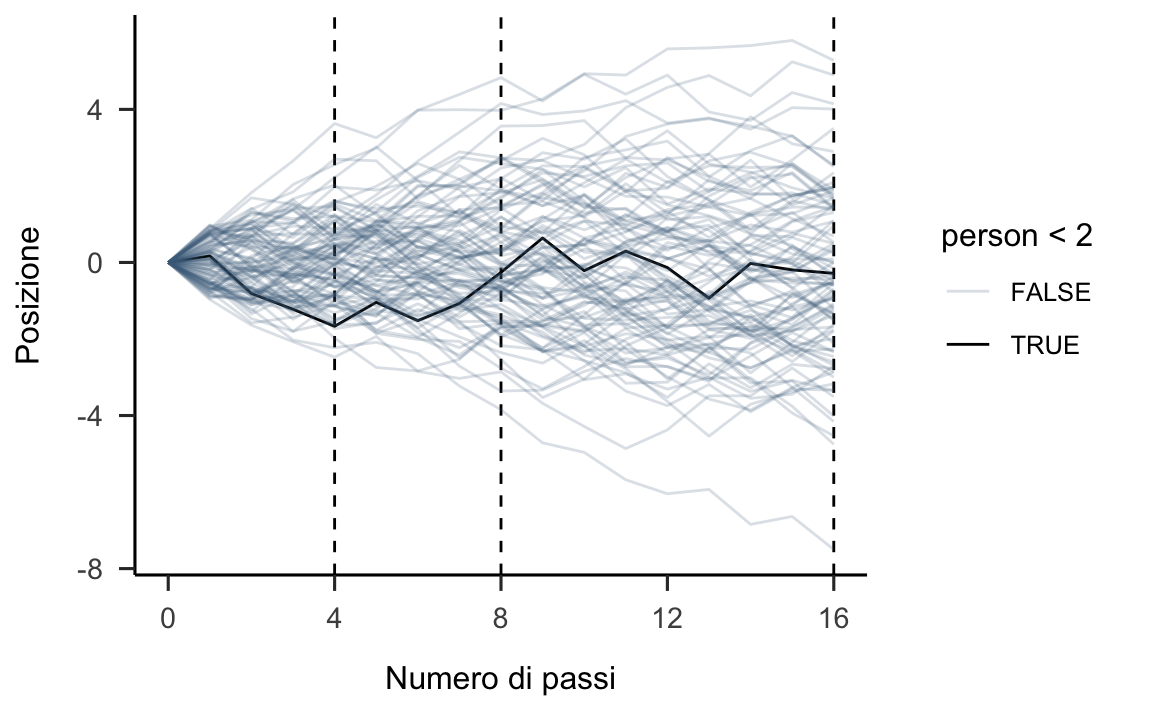
# Figure 4.2.a.
p1 <-
pos %>%
filter(step == 4) %>%
ggplot(aes(x = position)) +
geom_line(stat = "density", color = "dodgerblue1") +
labs(title = "4 steps")
# Figure 4.2.b.
p2 <-
pos %>%
filter(step == 8) %>%
ggplot(aes(x = position)) +
geom_density(color = "dodgerblue2", outline.type = "full") +
labs(title = "8 steps")
# this is an intermediary step to get an SD value
sd <-
pos %>%
filter(step == 16) %>%
summarise(sd = sd(position)) %>%
pull(sd)
# Figure 4.2.c.
p3 <-
pos %>%
filter(step == 16) %>%
ggplot(aes(x = position)) +
stat_function(fun = dnorm,
args = list(mean = 0, sd = sd),
linetype = 2) +
geom_density(color = "transparent", fill = "dodgerblue3", alpha = 1/2) +
labs(title = "16 steps",
y = "density")
library("patchwork")
# combine the ggplots
(p1 | p2 | p3) & coord_cartesian(xlim = c(-6, 6))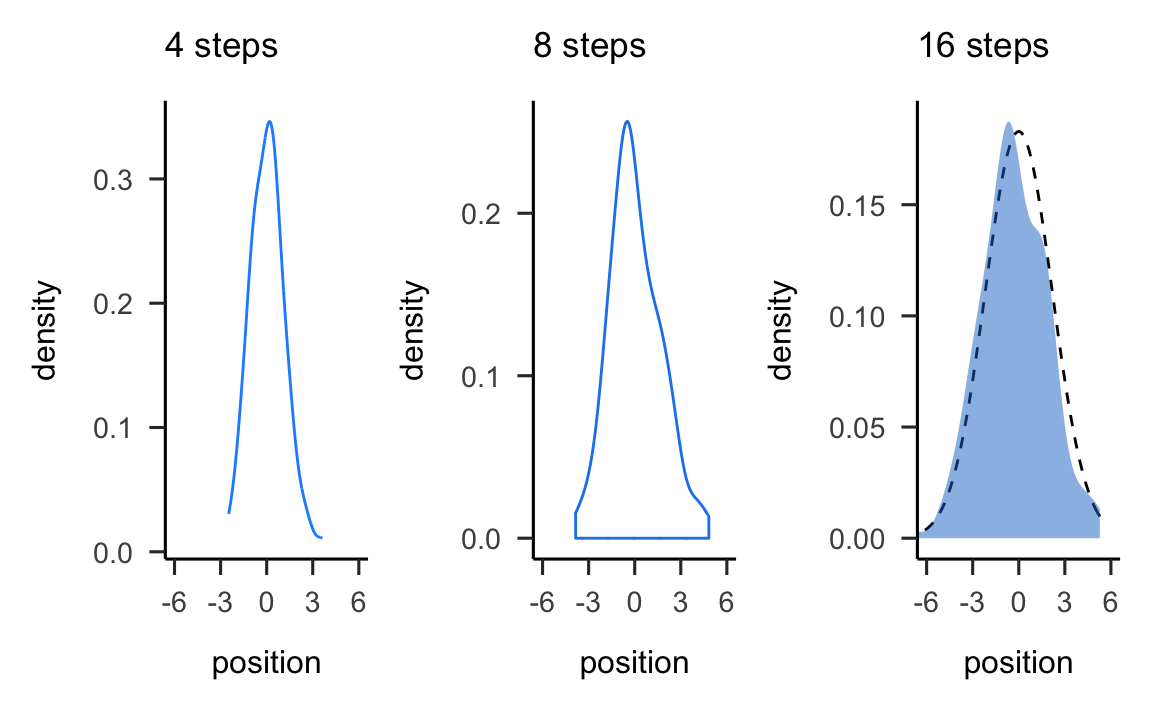
Questa simulazione mostra che qualunque processo nel quale viene sommato un certo numero di valori casuali, tutti provenienti dalla medesima distribuzione, converge ad una distribuzione Normale. Non importa quale sia la forma della distribuzione soggiacente. Può essere uniforme, come nell’esempio presente, o qualunque altra cosa. La forma della distribuzione soggiacente determina la velocità con cui si realizza la convergenza alla Normale. In alcuni casi la convergenza è lenta; in altri casi, come nell’esempio presente, la convergenza è molto rapida.
La distribuzione Normale è importante, in primo luogo, perché molti fenomeni naturali hanno approssimativamente le caratteristiche descritte dall’esempio precedente. In secondo luogo, è importante perché molti modelli statistici assumono che il fenomeno aleatorio di interesse abbia una distribuzione Normale. Da un punto di vista formale, una variabile aleatoria continua \(X\) si dice Normale se la sua funzione di densità è \[ f(x; \mu, \sigma) = {1 \over {\sigma\sqrt{2\pi} }} \exp \left\{-\frac{(x- \mu)^2}{2 \sigma^2} \right\}, \] dove \(\mu \in \Real\) e \(\sigma > 0\) sono due parametri. La curva di Gauss è unimodale e simmetrica con una caratteristica forma a campana e con il punto di massima densità in corrispondenza di \(\mu\). Il significato dei parametri \(\mu\) e \(\sigma\) che appaiono nella distribuzione Normale viene chiarito dalla dimostrazione che \[ \mathbb{E}(X) = \mu, \qquad var(X) = \sigma^2. \]
18.1.1 Concentrazione della distribuzione Normale
È istruttivo osservare il grado di concentrazione della distribuzione Normale attorno alla media: \[ \begin{aligned} P(\mu - \sigma < X < \mu + \sigma) &= P (-1 < Z < 1) \simeq 0.683, \notag\\ P(\mu - 2\sigma < X < \mu + 2\sigma) &= P (-2 < Z < 2) \simeq 0.956, \notag\\ P(\mu - 3\sigma < X < \mu + 3\sigma) &= P (-3 < Z < 3) \simeq 0.997. \notag \end{aligned} \] Si noti come un dato la cui distanza dalla media è superiore a 3 volte la deviazione standard presenti un carattere di eccezionalità perché meno del 0.3% dei dati della distribuzione Normale presentano questa caratteristica.
Per indicare la distribuzione Normale si usa la notazione \(\mathcal{N}(\mu, \sigma)\). La distribuzione Normale di parametri \(\mu = 0\) e \(\sigma = 1\) viene detta distribuzione Normale standard. La famiglia Normale è l’insieme avente come elementi tutte le distribuzioni Normali con parametri \(\mu\) e \(\sigma\) diversi. Tutte le distribuzioni Normali si ottengono dalla Normale standard mediante una trasformazione lineare: se \(X \sim \mathcal{N}(\mu_X, \sigma_X)\) allora \(Y = a + b X \sim \mathcal{N}(\mu_Y = a+b \mu_X, \sigma_Y = \left|b\right|\sigma_X)\).
18.1.2 Funzione di ripartizione della distribuzione Normale
Il valore della funzione di ripartizione di \(X\) nel punto \(x\) è l’area sottesa alla curva di densità \(f(x)\) nella semiretta \((-\infty, x]\). Non esiste alcuna funzione elementare per la funzione di ripartizione
\[ F(x) = \int_{-\infty}^x {1 \over {\sigma\sqrt{2\pi} }} \exp \left\{-\frac{(x- \mu)^2}{2\sigma^2} \right\} dx, \notag \] pertanto le probabilità \(P(X < x)\) vengono calcolate mediante integrazione numerica approssimata. I valori della funzione di ripartizione di una variabile aleatoria Normale sono dunque forniti da un software (in passato venivano forniti dalle tavole riportate sui testi di statistica).
Esercizio. Possiamo usare R per calcolare la funzione di ripartizione della Normale e per replicare i risultati che abbiamo presentato sopra.
La funzione pnorm(q, mean, sd) restituisce la funzione di ripartizione della Normale con media mean e deviazione standard sd, ovvero l’area sottesa alla funzione di densità di una Normale con media mean e deviazione standard sd nell’intervallo \([-\infty, q]\).
Per esempio, in precedenza abbiamo detto che il 68% circa dell’area sottesa ad una Normale è compresa nell’intervallo \(\mu \pm \sigma\). Verifichiamo per la distribuzione del QI:
Il 95% dell’area è compresa nell’intervallo \(\mu \pm 1.96 \cdot\sigma\):
Quasi tutta la distribuzione è compresa nell’intervallo \(\mu \pm 3 \cdot\sigma\):
18.1.3 Standardizzazione
Per potere utilizzare i valori tabulati (ma soprattutto per altri scopi più utili) si ricorre al procedimento di standardizzazione che riconduce una variabile aleatoria distribuita secondo una media \(\mu\) e varianza \(\sigma^2\), ad una variabile aleatoria con distribuzione “standard,” ovvero di media zero e varianza pari a \(1\):
\[ Z = \frac{X - \mu}{\sigma}. \]
L’area sottesa alla curva di densità di \(X\) nella semiretta \((-\infty, x]\) è uguale all’area sottesa alla densità Normale standard nella semiretta \((-\infty, z]\), in cui \(z = (x -\mu_X )/\sigma_X\) è il punteggio standard di \(x\). Per la simmetria della distribuzione, l’area sottesa nella semiretta \([1, \infty)\) è uguale all’area sottesa nella semiretta \((-\infty, 1]\) e quest’ultima coincide con \(F(-1)\). Analogamente, l’area sottesa nell’intervallo \([x_a, x_b]\), con \(x_a < x_b\), è pari a \(F(z_b) - F(z_a)\), dove \(z_a\) e \(z_b\) sono i punteggi standard di \(x_a\) e \(x_b\).
Si ha anche il problema inverso rispetto a quello del calcolo delle aree: dato un numero \(0 \leq p \leq 1\), il problema è quello di determinare un numero \(z \in \Real\) tale che \(P(Z < z) = p\). Il valore \(z\) cercato è detto quantile di ordine \(p\) della Normale standard ed è tabulato nelle tavole statistiche o può essere trovato mediante un software.
Esempio. Supponiamo che l’altezza degli individui adulti segua la distribuzione Normale di media \(\mu = 1.7\) m e deviazione standard \(\sigma = 0.1\) m. Vogliamo sapere la proporzione di individui adulti con un’altezza compresa tra \(1.7\) e \(1.8\) m.
Il problema ci chiede di trovare l’area sottesa alla distribuzione \(\mathcal{N}(\mu = 1.7, \sigma = 0.1)\) nell’intervallo \([1.7, 1.8]\):
library("gghighlight")
df <- data.frame(x = seq(1.4, 2.0, length.out = 100)) %>%
mutate(y = dnorm(x, mean=1.7, sd=0.1))
ggplot(df, aes(x, y)) +
geom_area(fill = "sky blue") +
gghighlight(x < 1.8 & x > 1.7) +
labs(
x = "Altezza",
y = "Densità"
)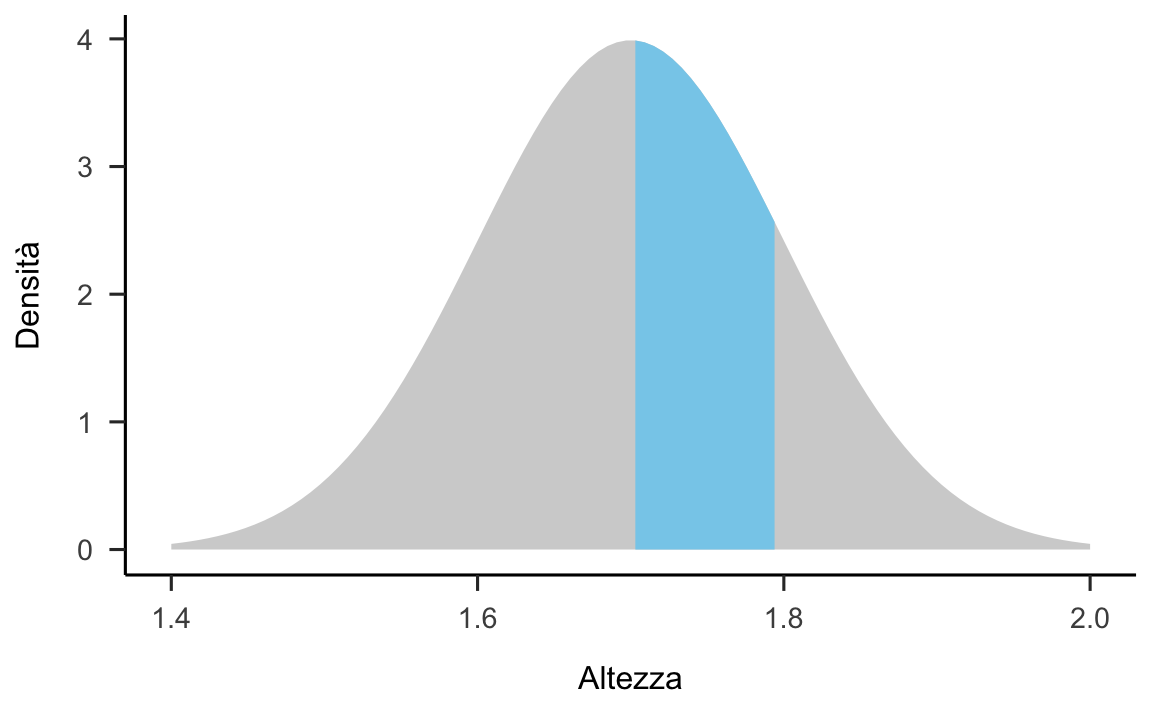
La risposta si trova utilizzando la funzione di ripartizione \(F(X)\) della legge \(\mathcal{N}(1.7, 0.1)\) in corrispondenza dei due valori forniti dal problema: \(F(X = 1.8) - F(X = 1.7)\). Utilizzando la seguente istruzione
otteniamo il \(31.43\%\).
In maniera equivalente, possiamo standardizzare i valori che delimitano l’intervallo considerato e utilizzare la funzione di ripartizione della normale standardizzata. I limiti inferiore e superiore dell’intervallo sono
\[ z_{\text{inf}} = \frac{1.7 - 1.7}{0.1} = 0, \quad z_{\text{sup}} = \frac{1.8 - 1.7}{0.1} = 1.0, \] quindi otteniamo
Il modo più semplice per risolvere questo problema resta comunque quello di rendersi conto che la probabilità richiesta non è altro che la metà dell’area sottesa dalle distribuzioni Normali nell’intervallo \([\mu - \sigma, \mu + \sigma]\), ovvero \(0.683/2\).
18.2 Distribuzione Chi-quadrato
La distribuzione con \(\chi^2_{~\nu}\) descrive la variabile aleatoria \[ Z_1^2 + Z_2^2 + \dots + Z_k^2, \] dove \(Z_1, Z_2, \dots, Z_k\) sono variabili aleatorie i.i.d. con distribuzione Normale standard \(\mathcal{N}(0, 1)\). La variabile aleatoria chi-quadrato dipende dal parametro intero positivo \(\nu = k\) che ne identifica il numero di gradi di libertà. La densità di probabilità di \(\chi^2_{~\nu}\) è \[ f(x) = C_{\nu} x^{\nu/2-1} \exp (-x/2), \qquad \text{se } x > 0, \] dove \(C_{\nu}\) è una costante positiva.
- La distribuzione di densità \(\chi^2_{~\nu}\) è asimmetrica.
- Il valore atteso di una variabile \(\chi^2_{~\nu}\) è uguale a \(\nu\).
- La varianza di una variabile \(\chi^2_{~\nu}\) è uguale a \(2\nu\).
- Per \(k \rightarrow \infty\), la \(\chi^2_{~\nu} \rightarrow \mathcal{N}\).
Una caratteristica importante della distribuzione chi-quadrato è la seguente: se \(X\) e \(Y\) sono due variabili aleatorie chi-quadrato indipendenti con \(\nu_1\) e \(\nu_2\) gradi di libertà, ne segue che \(X + Y \sim \chi^2_m\), con \(m = \nu_1 + \nu_2\). Tale principio si estende a qualunque numero finito di variabili aleatorie chi-quadrato indipendenti.
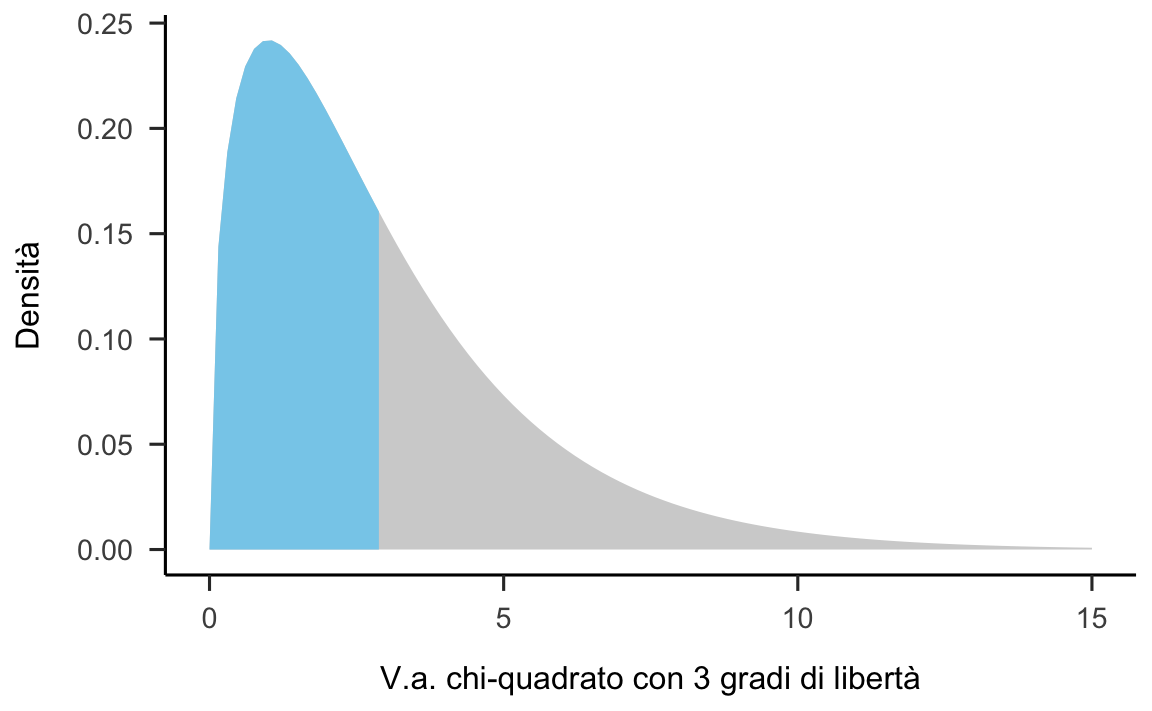
Esempio. Usiamo R per disegnare la densità chi-quadrato con 3 gradi di libertà. Usiamo due colori per l’area sottesa alla densità così da suddividenderla in due parti uguali.
df <- data.frame(x = seq(0, 15.0, length.out = 100)) %>%
mutate(y = dchisq(x, 3))
ggplot(df, aes(x, y)) +
geom_area(fill = "sky blue") +
gghighlight(x < 3) +
labs(
x = "V.a. chi-quadrato con 3 gradi di libertà",
y = "Densità"
)
18.3 Distribuzione \(t\) di Student
Se \(Z \sim \mathcal{N}\) e \(W \sim \chi^2_{~\nu}\) sono due variabili aleatorie indipendenti, allora il rapporto \[ T = \frac{Z}{\Big( \frac{W}{\nu}\Big)^{\frac{1}{2}}} \] definisce la distribuzione \(t\) di Student con \(\nu\) gradi di libertà.
Si usa scrivere \(T \sim t_{\nu}\). L’andamento della distribuzione \(t\) di Student è simile a quello della distribuzione Normale, ma ha una maggiore dispersione (ha le code più pesanti di una Normale, ovvero ha una varianza maggiore di 1).
La variabile \(t\) di Student soddisfa le seguenti proprietà:
Per \(\nu \rightarrow \infty\), \(t_{\nu}\) tende alla normale standard \(\mathcal{N}(0, 1)\).
La densità della \(t_{\nu}\) è una funzione simmetrica con valore atteso nullo.
Per \(\nu > 2\), la varianza della \(t_{\nu}\) vale \(\nu/(\nu - 2)\); pertanto è sempre maggiore di 1 e tende a 1 per \(\nu \rightarrow \infty\).
Esempio. Una rappresentazione di alcune distribuzioni \(t\) di Student è fornita nella figura seguente.
p = seq(-3, 3, length=100)
plot(p, dnorm(p, 0, 1), ylab="density", type ="l", col=4)
lines(p, dt(p, 2), type ="l", col=3)
lines(p, dt(p, 5), type ="l", col=2)
lines(p, dt(p, 30), col=1)
legend(1.5, .4, c("N(0,1)", "t(2)","t(5)","t(30)"), lty=c(1,1,1,1),col=c(4,3,2,1))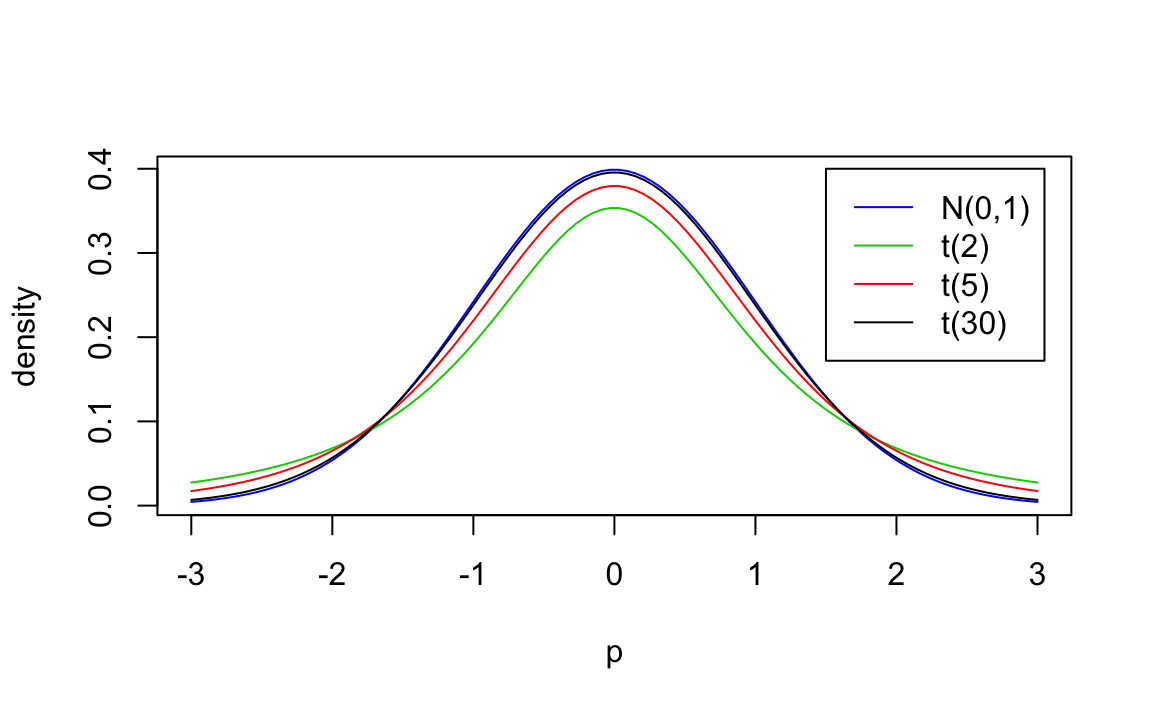
18.4 Distribuzione Beta
La distribuzione Beta è una distribuzione definita nell’intervallo \[0, 1\]. La distribuzione Beta ha due parametri, che chiameremo \(a\) e \(b\). Questi due parametri determinano la forma delle distribuzioni Beta (proprio come la media e la varianza determinano la forma della distribuzione normale). Seguendo la consueta convenzione, si scrive \(X \sim Beta(a, b)\) come abbreviazione di “\(X\) ha una distribuzione Beta di parametri \(a\) e \(b\).”
Se \(X \sim Beta(a, b)\), allora la densità di \(X\) è \[ f_X(x) = \frac{1}{B(a, b)} x^{a-1} (1-x)^{b-1} \qquad x \in [0, 1]. \] laddove \(B(a, b)\) è conosciuta come la “funzione beta” e corrisponde ad una costante (in quanto non dipende da \(x\)), il cui scopo è che la densità si integri a 1, come deve essere per tutte le funzioni di densità.
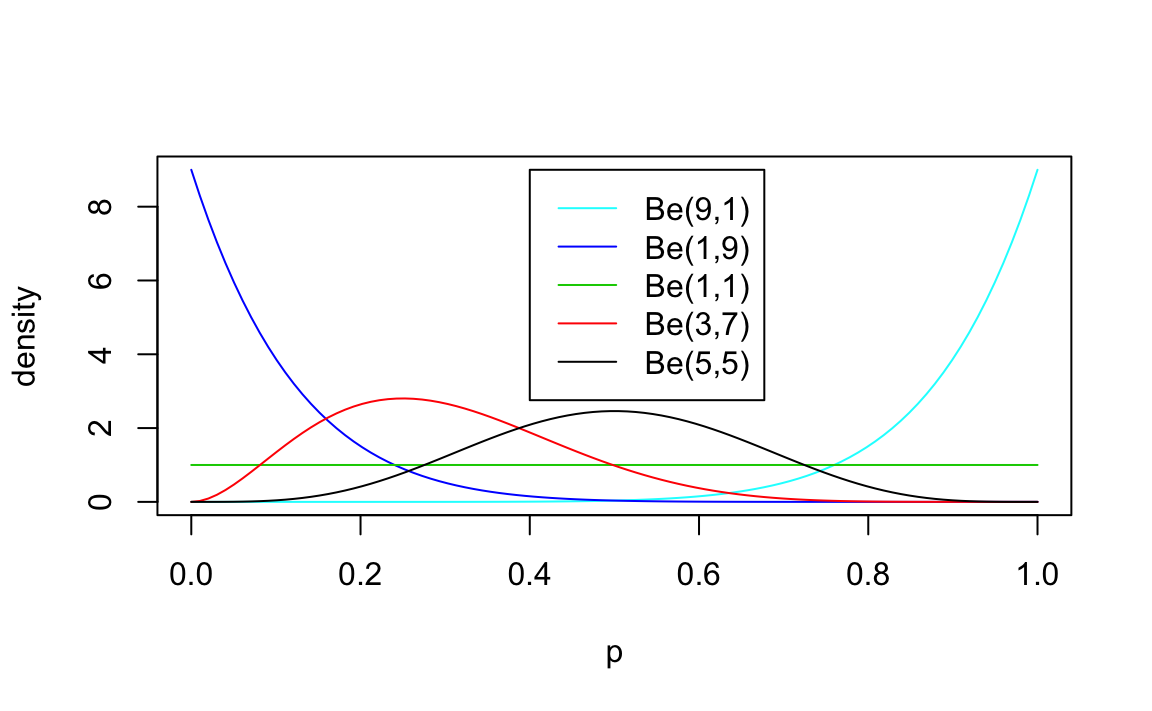
Esempio. Una rappresentazione di alcune distribuzioni Beta è fornita nella figura seguente.
p = seq(0,1, length=100)
plot(p, dbeta(p, 9, 1), ylab="density", type ="l", col=5)
lines(p, dbeta(p, 1, 9), type ="l", col=4)
lines(p, dbeta(p, 1, 1), col=3)
lines(p, dbeta(p, 3, 7), col=2)
lines(p, dbeta(p, 5, 5), col=1)
legend(0.4,9, c("Be(9,1)","Be(1,9)","Be(1,1)", "Be(3,7)", "Be(5,5)"),lty=c(1,1,1,1,1),col=c(5,4,3,2,1))