Capitolo 13 Il calcolo delle probabilità
È normale fare delle congetture rispetto a ciò di cui non siamo sicuri. Ma perché facciamo questo? Molto spesso perché, anche se sappiamo che le nostre conoscenze sono incomplete, dobbiamo comunque prendere delle decisioni. Ad esempio: “non so se tra qualche ora pioverà; devo o non devo prendere l’ombrello?” In maniera simile, anche se uno psicologo non sa in maniera certa quali sono i meccanismi che regolano i fenomeni psicologi, deve comunque decidere tra diverse alternative. Per esempio, deve fornire un parere, relativamente a chi, tra due genitori, sia più adatto per ottenere l’affidamento del figlio in caso di divorzio, oppure quale sia, in un caso specifico, l’approccio più efficace per il trattamento dei disturbi dell’alimentazione. Ovviamente la qualità delle congetture varia, così come varia la qualità delle decisioni che prendiamo. La teoria delle probabilità ci fornisce gli strumenti per prendere decisioni “razionali” in condizioni di incertezza, ovvero per formulare le migliori congetture possibili.
La teoria delle probabilità ci consente di descrivere in maniera quantitativa quei fenomeni che, pur essendo altamente variabili, rivelano comunque una qualche coerenza a lungo termine. Il lancio ripetuto di una moneta è uno di questi fenomeni. È anche l’esempio tipico che viene usato per introdurre una discussione sulle probabilità. Sapere se una moneta sia onesta o meno, o calcolare la probabilità di ottenere testa un certo numero di volte può essere interessante nel mondo delle scommesse, ma nella vita quotidiana non ci capita spesso di lanciare una moneta per prendere una decisione. Allora perché ci preoccupiamo di studiare le proprietà statistiche dei lanci di una moneta? A questa domanda si può rispondere dicendo che l’esperimento (chiamato “casuale”) che corrisponde al lancio di una moneta è il surrogato di una molteplicità di eventi che, della vita reale, sono molto importanti. Per esempio: qual è la probabilità di successo di un intervento psicologico? Qual è la probabilità che un test per l’HIV dia esito positivo in una persona che non ha l’HIV? Qual è la probabilità di essere occupato entro un anno dalla laurea? I lanci di una moneta costituiscono una rappresentazione generica di molteplici altri eventi che hanno un grande significato nella nostra vita. Questa è la ragione per cui studiamo le proprietà statistiche dei fenomeni aleatori usando il lancio di una moneta quale esempio generico.
La discussione della teoria della probabilità è certamente l’argomento più impegnativo affrontato in queste dispense. Fare uno sforzo di comprensione per chiarire i concetti di base della teoria della probabilità è però necessario per mettersi nelle condizioni di capire le caratteristiche dell’inferenza statistica che verranno discusse in seguito.
13.1 Probabilità nel linguaggio naturale
In un articolo pubblicato su Harward Business Review nel 2018, Mauboussin e Mauboussin ci ricordano come, nel marzo del 1951, l’Office of National Estimates della CIA pubblicò un documento che suggeriva che un attacco sovietico alla Jugoslavia nel corso dell’anno fosse una “seria possibilità.” Sherman Kent, un professore di storia a Yale che fu chiamato a Washington, D.C. per dirigere l’Office of National Estimates, espresse perplessità sull’esatto significato dell’espressione “seria possibilità.” Lo interpretò nel senso che la probabilità di un attacco era di circa il 65%. Ma quando chiese ai membri del Board of National Estimates cosa ne pensassero, gli furono riferite cifre che andavano dal 20% all’80%. Una gamma così ampia rappresentava chiaramente un problema, poiché le implicazioni politiche di quegli estremi erano nettamente diverse. Kent riconobbe che la soluzione di tale problema era quella di usare i numeri per esprimere il nostro grado di certezza, notando mestamente:
Non abbiamo usato i numeri… e sembra chiaro che abbiamo abusando delle parole.
Da allora non è cambiato molto. Ancora oggi le persone nel mondo della politica, degli affari e nella vita quotidiana continuano a usare parole vaghe per descrivere i possibili risultati degli eventi. Perché? Phil Tetlock, professore di psicologia all’Università della Pennsylvania, che ha studiato a fondo il fenomeno psicologico della previsione, suggerisce che “una vaga verbosità conferisce sicurezza.” Quando usiamo una parola per descrivere la probabilità di un evento incerto, cerchiamo di porci nelle condizioni di non essere smentiti dopo che il risultato dell’evento verrà rivelato. Se si verifica l’evento che abbiamo previsto, è facile dire: “Ti avevo detto che probabilmente sarebbe successo questo.” Se la nostra predizione fallisce, possiamo sempre dire: “Ho solo detto che probabilmente sarebbe successo.” Parole così ambigue non solo consentono all’oratore di evitare di essere smentito, ma consentono anche al destinatario di interpretare il messaggio in modo coerente con le sue nozioni preconcette. Ovviamente, da tale ambiguità linguistica deriva una cattiva comunicazione. È dunque necessario procedere in modo diverso nel linguaggio scientifico. Vedremo in questo capitolo come sia possibile assegnare al termine “probabilità” un significato preciso.
13.2 Probabilità nel linguaggio scientifico
La teoria della probabilità nasce nel 1654. Fu infatti in questa data che Antoine Gombaud Cavalier De Méré, un nobile francese, nonché accanito giocatore d’azzardo scrisse una lettera al suo amico Pascal per cercare di comprendere il motivo delle sue continue perdite nel gioco dei dadi. De Méré descrisse due diverse scommesse:
- scommessa A
-
si lancia un dado per 4 volte di seguito e si vince se esce almeno una volta il 6;
- scommessa B
-
si lanciano due dadi per 24 volte di seguito e si vince se esce almeno una volta il doppio 6.
Il cavaliere De Méré pose a Pascal il seguente quesito: le possibilità di vittoria sono maggiori nella scommessa A o nella scommessa B? Il problema di De Méré divenne un motivo di scambio epistolare tra Pascal e Fermat, i due più grandi matematici del tempo, e viene considerato come la motivazione iniziale dello sviluppo della teoria della probabilità.
Ma come può essere risolto il problema di De Méré? Una strategia possibile è quella di seguire l’esempio di De Méré, ovvero, giocare questo gioco molte volte. Così facendo, De Méré si rese conto che le possibilità di vittoria erano leggermente migliori nel caso della scommessa A.
Utilizzando una simulazione al computer possiamo facilmente giungere a questa stessa conclusione senza perdere tutto il tempo che De Méré ha dedicato a questa materia. Una simulazione al computer ci consente infatti di ripetere il gioco di De Méré moltissime volte e di annotare il risultato ottenuto ad ogni ripetizione del gioco. Vedremo in seguito perché, utilizzando un computer, è possibile ottenere un risultato diverso ogni volta che si ripete una certa operazione, in modo tale da rappresentare il grado di casualità che si osserva quando si lancia di un dado. Per ora ci limitiamo ad esaminare i risultati che vengono prodotti in questo modo e che sono illustrati nella figura 13.1.
# Game A: Throw a fair die at most four times, and win if you get a six.
experiment_a <- function(){
rolls <- sample(1:6, size = 4, replace = TRUE)
condition <- sum(rolls == 6) > 0
return(condition)
}
# Game B: Throw two fair dice at most twenty-four times, and win if you get a double-six.
experiment_b <- function(){
first.die <- sample(1:6, size = 24, replace = TRUE)
second.die <- sample(1:6, size = 24, replace = TRUE)
condition <- sum((first.die == second.die) & (first.die == 6)) > 0
return(condition)
}
# number of replications
nrep <- 1e4
# Play game A nrep times. We get a vector of nrep elements. Eeach element of
# of the simsA vector is the outcome obtained by playing game A once: TRUE if
# the output is a win, FALSE if the output of the game is a loss. Remember than
# TRUE = 1 and FALSE = 0.
sims_a <- replicate(nrep, experiment_a())
# The proportion of wins in game A
prop_wins_a <- sum(sims_a)/length(sims_a)
prop_wins_a
#> [1] 0.5193
# To plot the results, we compute the
nwins_a <- cumsum(sims_a)
ntrials <- 1:nrep
sims_b <- replicate(nrep, experiment_b())
prop_wins_b <- sum(sims_b)/length(sims_b)
prop_wins_b
#> [1] 0.493
nwins_b <- cumsum(sims_b)
d <- data.frame(
n = c(ntrials, ntrials),
pwin = c(nwins_a/ntrials, nwins_b/ntrials),
game = rep(c("Scommessa A", "Scommessa B"), each = nrep)
)
d %>%
ggplot(
aes(x = n, y = pwin, col = game)
) +
geom_point(alpha = 0.4) +
geom_line() +
scale_x_log10(breaks = c(1, 3, 10, 50, 200, 1000, 3000, 10000)) +
theme(legend.title = element_blank()) +
labs(
x="Numero di ripetizioni del gioco di De Méré",
y="Proporzione di vincite") +
scale_color_manual(values = c("gray80", "skyblue")) +
theme(legend.position = "bottom")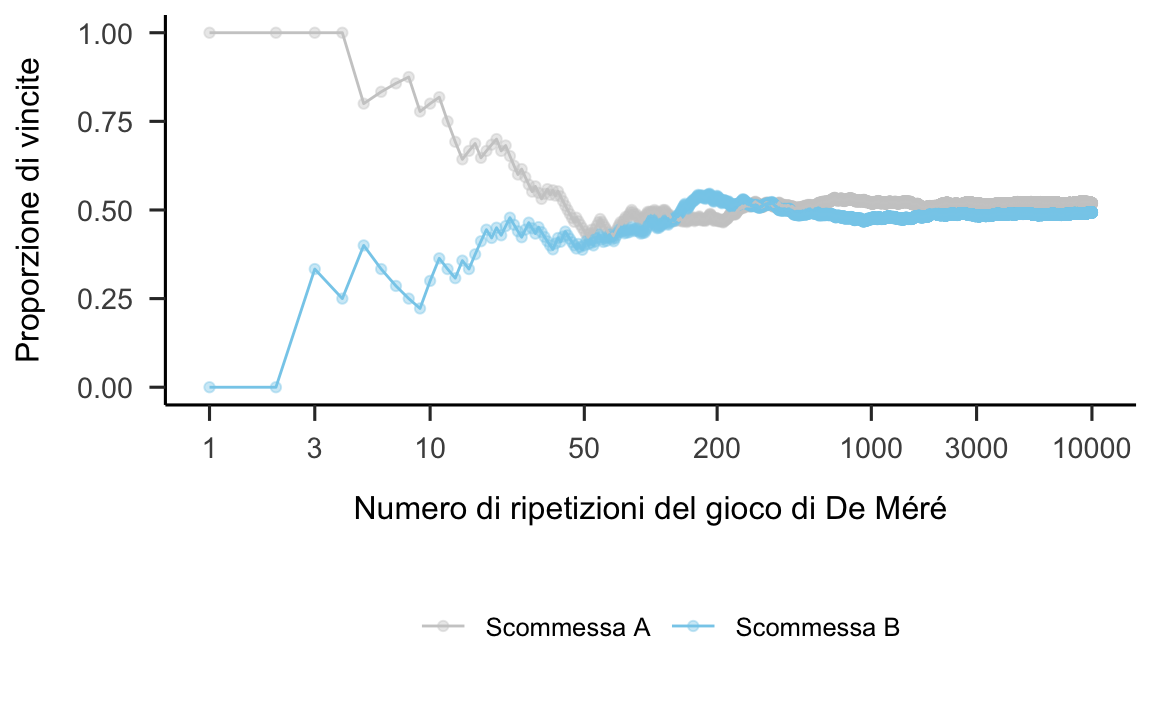
Figura 13.1: Risultati ottenuti da 10000 ripetizioni delle due scommesse di De Méré.
La figura 13.1 riportata la proporzione di vittorie in funzione del numero di ripetizioni di ciascuna scommessa e rivela che, a lungo termine (ovvero, se consideriamo un grande numero di ripetizioni del gioco di De Méré), la scommessa A risulta più conveniente della scommessa B. Nel caso di 10000 ripetizioni del gioco di De Méré, la proporzione di vittorie è risultata essere pari a 0.5182 per la scommessa A e pari a 0.4909 per la scommessa B. Se ripetiamo la stessa simulazione altre 10000 volte, otteniamo una proporzione di vittorie uguale a 0.5180 per la scommessa A e a 0.4878 per la scommessa B.
Vedremo in questo capitolo come ciascuna di queste proporzioni possa essere considerata come una stima empirica di ciò che chiamiamo probabilità. Le proporzioni descritte sopra vengono sono delle “stime” poiché approssimano il vero valore della probabilità; infatti, ripetendo la simulazione due volte abbiamo ottenuto dei risultati leggermente diversi. Ma allora qual è il “vero” valore della probabilità? Un modo semplice per rispondere a questa domanda è quello di dire che, utilizzando la procedura descritta sopra, il vero valore della probabilità si otterrebbe se il gioco di De Méré venisse ripetuto infinite volte. Ma ovviamente, per qualunque applicazione concreta, non abbiamo bisogno di ripetere la simulazione infinite volte, in quanto un grande numero di ripetizioni ci fornisce un’approssimazione sufficiente.
In conclusione, le considerazioni precedenti ci fanno capire che il concetto di probabilità sia legato a quello di incertezza. La probabilità può infatti essere definita come la quantificazione del livello di “casualità” di un evento, laddove viene detto casuale ciò che non è noto o non può essere predetto con certezza.
13.3 Terminologia
Come qualsiasi altra branca della matematica, la teoria delle probabilità fa uso di una specifica terminologia i cui concetti di base sono descritti di seguito.
- Il calcolo delle probabilità si occupa di un generico esperimento casuale. Si dice esperimento casuale qualsiasi attività che produce un risultato osservabile. L’esecuzione di un esperimento casuale è chiamata prova dell’esperimento. Esempi sono: lanciare una moneta, lanciare un dado a 6 facce, provare un nuovo percorso per andare al lavoro per vedere se è più veloce di quello che usiamo di solito, o giocare al gioco di De Méré.
- Il risultato (o esito) di una prova si indica con \(\omega\) ed è detto evento elementare.
- Prima che l’esperimento casuale venga eseguito non sappiamo quale esito verrà prodotto; dopo che l’esperimento casuale è stato eseguito, l’esito dell’esperimento si “cristallizza” nel risultato osservato.
- Si dice spazio campionario \(\Omega\) (probability space) l’insieme di tutti i possibili esiti di un esperimento casuale. Lo spazio campionario può essere finito, infinito o infinito numerabile. Eseguire un esperimento casuale significa scegliere in maniera casuale uno dei possibili eventi elementari dello spazio campionario.
- Si dice evento composto (o non-elementare) un sottoinsieme dello spazio campionario, ovvero un insieme che può essere a sua volta scomposto in più eventi elementari. Per esempio, il numero 4 è un evento elementare dello spazio campionario finito \(\Omega = \{1, 2, 3, 4, 5, 6\}\) che corrisponde all’esperimento casuale del lancio di un dado. L’evento composto \(A\) “il risultato è pari” è \(A = \{2, 4, 6\}\).
13.4 Le diverse definizioni della probabilità
Ma, nello specifico, che cos’è la probabilità? A questa domanda si può rispondere in modi diversi.
13.4.1 Una definizione ingenua della probabilità
Storicamente, la prima definizione della probabilità di un evento è stata quella che richiede di contare il numero di modi nei quali un evento può manifestarsi e di dividere tale numero per il numero totale di eventi dello spazio campionario \(\Omega\).
La definizione 13.1 rende chiaro che il calcolo delle probabilità richiede di contare il numero di modi in cui un evento può realizzarsi. Per esempio, nell’esperimento casuale corrispondente al lancio di due dadi equilibrati, l’evento \(A\) = “la somma dei due dati è 5” si può realizzare in 4 modi diversi: \(A = \{ (1, 4), (2, 3), (3, 2), (4, 1) \}\). Contare il numero di modi in cui un evento può realizzarsi può essere semplice, nel caso di alcuni eventi (come il presente), oppure estremamente complesso, nel caso di altri eventi. In questo secondo caso, per contare il numero di modi in cui un evento può realizzarsi, al fine di calcolare la probabilità definita come indicato sopra, è necessario fare uso del calcolo combinatorio. In queste dispense ci accontenteremo di presentare alcune nozioni di base del calcolo combinatorio, ma non entreremo nei dettagli di questo argomento.
13.4.2 Una definizione non ingenua della probabilità
Il calcolo combinatorio ci consente di contare il numero di casi nello spazio campionario e di applicare la definizione “ingenua” di probabilità descritta nella definizione 13.1. È però facile rendersi conto che tale definizione di probabilità ha un grosso problema: non può essere applicata al caso di uno spazio campionario infinito. Dobbiamo dunque trovare una definizione che risolva un tale problema.
L’attuale nozione matematica di probabilità ha impiegato diverse centinaia di anni per cristallizzarsi. Non cerca di rispondere a difficili domande filosofiche come “Che cos’è la casualità?” “Da dove viene?” “Qual è il significato della probabilità nel mondo reale?” ecc., ma ci offre un modello matematico che si rivela estremamente efficace nella modellazione dei fenomeni del mondo reale.
Nella maggior parte dei trattamenti matematici contemporanei della probabilità, la nozione di base è quella uno spazio di probabilità, che è un modello matematico di un esperimento casuale. Esempi di un esperimento casuale sono tre lanci successivi di una moneta equilibrata o la scelta di un punto casuale in un quadrato di area unitaria.
Uno spazio di probabilità è una tripla (\(\Omega\), \(\mathcal{F}\), \(P\)). La prima componente viene chiamata spazio campionario ed è un insieme costituito da tutti i possibili risultati dell’esperimento casuale. Ogni elemento \(\omega \in \Omega\) è chiamato evento elementare. Per l’esempio dei tre lanci di una moneta, lo spazio campionario consiste di tutte le possibili sequenze di tre lettere costituite da H (testa) e T (croce): \(\Omega\) = {HHH, HHT, …, TTT}. Per l’esempio della scelta di un punto casuale in un quadrato, lo spazio campionario è costituito da tutti i punti contenuti nell’area del quadrato.
La seconda componente \(\mathcal{F}\) di uno spazio di probabilità è un insieme di sottoinsiemi di \(\Omega\). Ogni insieme \(E \in \mathcal{F}\) è chiamata evento. Un esempio concreto di evento nell’esperimento dei tre lanci di una moneta è “numero dispari di risultati croce,” ovvero \(E = {HHT, HTH, THH, TTT}\). Nell’esempio della scelta di un punto casuale in un quadrato, tutte le figure geometriche all’interno del quadrato sono degli eventi.
L’ultimo componente \(P\) di uno spazio di probabilità è una funzione che assegna un numero reale \(P(E)\), chiamato probabilità di \(E\), a ogni evento \(E \in \mathcal{F}\). Nell’esempio dei tre lanci di una moneta, consideriamo tutti gli eventi elementari egualmente probabili, e la probabilità di un evento \(E\) è definita come il rapporto tra il numero degli eventi elementari in \(E\) e il numero degli eventi elementari nello spazio campionario. Nell’esempio della scelta di un punto casuale in un quadrato, la probabilità dell’evento \(E\) che corrisponde ad una qualche figura geometrica inscritta nel quadrato è data dal rapporto tra l’area di tale figura geometrica e l’area totale del quadrato.
La tripla (\(\Omega\), \(\mathcal{F}\), \(P\)) deve soddisfare i seguenti assiomi, che furono presentati per la prima volta in questa forma da Kolmogorov negli anni ’30:
- \(P(E) ≥ 0\) per ciascun \(E \in \mathcal{F}\).
- \(P(\Omega) = 1\) (l’esperimento produce sempre qualche risultato).
- \(P\) se \(E_1, E_2, \dots\) è una sequenza di eventi mutuamente disgiunti, ne segue che \[ P\left(\bigcup\limits_{i=1}^{\infty} E_i \right) = \sum_{i=1}^\infty P(E_i) \]
Gli assiomi (1) e (2) sono molto intuitivi, così come l’additività nel caso di un numero finito di eventi. L’additività numerabile non può essere supportata dall’intuizione, ma è uno strumento fondamentale nella teoria della probabilità e della statistica.
La precedente definizione di uno spazio di probabilità corrisponde al cosiddetto approccio assiomatico messo a punto da Kolmogorov intorno al 1930, il quale è alla base della moderna teoria della probabilità. Gli assiomi di Kolmogorov sono necessari per evitare i paradossi che si possono creare quando si manipolano gli insiemi – ad esempio, l’utilizzo dell’“l’insieme di tutti gli insiemi” tipicamente conduce ad un paradosso.
13.5 Assegnare le probabilità agli eventi
È importante capire che l’approccio assiomatico non ci dice però come sia possibile assegnare un valore di probabilità a un evento \(E \in \Omega\). A questo proposito esistono due diverse scuole di pensiero.
13.5.1 Approccio frequentista
Una prima possibilità è di definire la nozione di probabilità in termini empirici. La probabilità di un evento \(A\) può essere concepita come il limite cui tende la frequenza relativa dell’evento, al tendere all’infinito del numero delle prove effettuate, ossia \[\begin{equation} P_A = \lim_{n \to \infty} \frac{n_A}{n}. \end{equation}\] Questo è l’approccio che abbiamo utilizzato in precedenza, quando abbiamo discusso il gioco di De Méré.
Tale definizione assume che l’esperimento possa essere ripetuto più volte, idealmente infinite volte, sotto le medesime condizioni, e corrisponde alla definizione frequentista di probabilità. Per l’approccio frequentista, dire che la probabilità di ottenere testa è 0.5 significa affermare che l’evento “testa” verrebbe ottenuto nel 50% dei casi, se ripetessimo tantissime volte l’esperimento casuale del lancio di una moneta.
Se non abbiamo a disposizione informazioni empiriche a proposito del verificarsi di un evento possiamo attribuire le probabilità agli eventi usando la nostra conoscenza della situazione. Tale approccio è seguito dalla definizione classica di probabilità in base alla quale la probabilità di un evento è il rapporto tra il numero di casi favorevoli e quelli possibili, supposto che tutti gli eventi siano equiprobabili, ossia \[ P_A = \frac{n_A}{n}, \] dove \(n\) è il numero di casi possibili e \(n_A\) è il numero di casi favorevoli per l’evento \(A\). L’assunzione di equiprobabilità degli eventi elementari ha senso soprattutto nel caso dei giochi d’azzardo.
In base all’approccio frequentista, la probabilità è il limite a cui tende una frequenza relativa empirica al crescere del numero di ripetizioni dell’esperimento casuale. È molto facile utilizzare per calcolare una tale probabilità. Per esempio, se vogliamo calcolare la probabilità di ottenere 3 nel lancio di un dado equilibrato, possiamo eseguire la seguente simulazione.
Il risultato è ovviamente molto simile a \(1/6\).
13.5.2 Approccio Bayesiano
Esistono però degli eventi per i quali non è possibile calcolare una frequenza relativa, ovvero quelli che si verificano una volta soltanto. Che cos’è allora la probabilità in questi casi? In base all’approccio Bayesiano la probabilità è una misura del grado di plausibilità di una proposizione. Questa definizione è applicabile a qualsiasi evento. Ciò consente di assegnare una probabilità anche a proposizioni quali “il candidato \(A\) vincerà le elezioni” oppure “l’accusato è innocente,” anche se non è possibile ripetere più volte un’elezione o un evento criminoso.
Per assegnare le probabilità agli eventi, nell’approccio Bayesiano si utilizzano considerazioni “soggettive” che derivano dalle informazioni di cui il soggetto è in possesso. Il teorema di Bayes consente di aggiustare, alla luce dei dati osservati, tali credenze “a priori” per arrivare alla probabilità a posteriori. Quindi, tramite l’approccio Bayesiano, si usa una stima del grado di plausibilità di una proposizione prima dell’osservazione dei dati, al fine di associare un valore numerico al grado di plausibilità di quella stessa proposizione successivamente all’osservazione dei dati. Questo processo di “aggiornamento Bayesiano” corrisponde all’inferenza statistica e verrà discusso in dettaglio nel seguito delle dispense.
13.6 Proprietà elementari della probabilità
Indipendentemente da come decidiamo di interpretare la probabilità (in termini frequentisti o Bayesiani), alla probabilità possono essere assegnate le seguenti proprietà.
La probabilità dell’evento impossibile è zero: \[P(\emptyset) = 1 - P(\Omega) = 0.\]
Se consideriamo due eventi \(A\) e \(B\) tali che \(A \subseteq B\), cioè che \(A\) è contenuto o coincidente con \(B\), da ciò segue che \[P(A) \leq P(B).\]
Se \(A^c\) è il complementare dell’evento \(A\), allora \[P(A^c) = 1 - P(A).\]
Dati \(n\) eventi \(A_i\) per \(i= 1, \cdots, n\), gli eventi si dicono indipendenti se risulta \[P(A_i \cap A_j \cap \cdots \cap A_k) = P(A_i) P(A_j) \cdots P(A_k).\]
Se due eventi \(A\) e \(B\) non sono disgiunti, allora quando sommiamo le loro probabilità dobbiamo evitare che la loro parte comune \(A \cap B\) venga contata due volte. Dati due eventi non necessariamente disgiunti, dunque, la probabilità dell’unione è pari alla somma delle singole probabilità dei due eventi meno la probabilità dell’intersezione: \[\begin{equation} P(A \text{ o } B) = P(A \cup B) = P(A) + P(B) - P(A \cap B). \tag{13.1} \end{equation}\]
13.7 Variabili aleatorie
Tutte le nozioni che abbiamo discusso in precedenza sono necessarie per potere definire il concetto di “variabile aleatoria.” Le variabili aleatorie sono un concetto fondamentale della teoria statistica e delle sue applicazioni. Infatti, le variabili aleatorie sono lo strumento che usiamo per valutare, per esempio, l’efficacia di un intervento psicologico. Un intervento psicologico, infatti, può essere concepito come un “esperimento casuale” e le variabili aleatorie ci consentono di riassumere i risultati di un esperimento casuale e di quantificare il grado di certezza che possiamo assegnare all’esito osservato, nel contesto di tutti gli esiti possibili che, in linea di principio, sarebbe stato possibile osservare. Il significato di “variabile aleatoria” è semplice; meno semplice è capire come manipolare le variabili aleatorie. Ma iniziamo con una definizione.
Il dominio della variabile aleatoria \(X\) (che è una funzione) è dato dai punti dello spazio campionario \(\Omega\). Ad ogni evento elementare \(\omega_i\) attribuiamo il numero \(X(\omega_i)\), ovvero il valore che la variabile aleatoria assume sul risultato \(\omega_i\) dell’esperimento casuale. L’attributo “aleatoria” si riferisce al fatto che la variabile considerata trae origine da un esperimento casuale di cui non siamo in grado di prevedere l’esito con certezza.
Mediante una variabile aleatoria trasformiamo lo spazio campionario \(\Omega\), che in genere è complesso, in uno spazio campionario più semplice formato da un insieme di numeri. Il maggior vantaggio di questa sostituzione è che molte variabili aleatorie, definite su spazi campionari anche molto diversi tra loro, danno luogo ad una stessa “distribuzione” di probabilità sull’asse reale. Le variabili aleatorie si indicano con le lettere maiuscole ed i valori da esse assunti con le lettere minuscole.
Ci sono due classi di variabili aleatorie: variabili aleatorie discrete e variabili aleatorie continue. Consideriamo innanzitutto il caso delle variabili aleatorie discrete.
Se \(X\) è una variabile aleatoria discreta allora l’insieme dei possibili valori \(x\), tali per cui \(P(X = x) > 0\), viene detto “supporto” di \(X\).
Alcuni esempi di variabili aleatorie discrete sono i seguenti: il numero di intrusioni di pensieri, immagini, impulsi indesiderabili in un paziente OCD, il voto all’esame di Psicometria, la durata di vita di un individuo, il numero dei punti che si osservano nel lancio di due dadi e il guadagno (la perdita) che un giocatore realizzerà in \(n\) partite. Si noti che, in tutti questi casi, la variabile aleatoria considerata viene rappresentata mediante un numero.
13.7.1 A cosa servono le variabili aleatorie?
Facendo riferimento agli esempi elencati sopra, possiamo chiederci perché questi numeri vengono considerati come “aleatori.” È ovvio che noi non conosciamo, ad esempio, il voto di Psicometria di Mario Rossi prima del momento in cui Mario Rossi avrà fatto l’esame. Le variabili aleatorie si pongono il seguente problema: come possiamo descrivere le nostre opinioni rispetto al voto (possibile) di Mario Rossi, prima che lui abbia fatto l’esame. Prima dell’esame, il voto di Psicometria di Mario Rossi si può solo descrivere facendo riferimento ad un insieme di valori possibili. Inoltre, molto spesso, possiamo anche dire che tali valori possibili non sono tutti egualmente verosimili: ci aspettiamo di osservare più spesso alcuni di questi valori rispetto agli altri. Le proprietà delle variabili aleatorie ci consentono di sistematizzare questo tipo di opinioni. Ovviamente, una volta che Mario Rossi avrà fatto l’esame, questa materia non avrà più alcuna componente aleatoria.
13.7.2 Funzione di massa di probabilità
Per entrare nel merito di questa discussione, chiediamoci ora come sia possibile associare delle probabilità ai valori che vengono assunti dalle variabili aleatorie. Ad esempio, qual è la probabilità che Mario Rossi ottenga 29 all’esame? Ci occuperemo qui del caso delle variabili aleatorie discrete.
Alle variabili aleatorie discrete vengono assegnale le probabilità mediante le cosiddette “distribuzioni di probabilità.” Una distribuzione di probabilità è un modello matematico che collega ciascun valore di una variabile aleatoria discreta alla probabilità di osservare un tale valore in un esperimento casuale. In pratica, ad ognuno dei valori che possono essere assunti da una variabile aleatoria discreta viene associata una determinata probabilità. La funzione che associa ad ogni valore della variabile aleatoria una probabilità corrispondente si chiama “distribuzione di probabilità” oppure “legge di probabilità.”
Una descrizione intuitiva del concetto di distribuzione di probabilità può essere formulata nei termini seguenti. Possiamo pensare alla probabilità come ad una quantità positiva che viene “distribuita” sull’insieme dei valori della variabile aleatoria. Tale “distribuzione” (suddivisione, spartizione) viene scalata in maniera tale che ciascun elemento di essa corrisponda ad una proporzione del totale, nel senso che il valore totale della distribuzione è sempre pari a 1. Una distribuzione di probabilità non è dunque altro che un modo per suddividere la nostra certezza (cioè 1) tra i valori che la variabile aleatoria può assumere. In modo più formale, possiamo dire quanto segue.
In maniera più semplice, una distribuzione di (massa) di probabilità è formata dall’elenco di tutti i valori possibili di una variabile aleatoria discreta e dalle probabilità loro associate. Si noti che \(P_{\pi}(X=x)\) è un numero positivo se il valore \(x\) è compreso nel supporto di \(X\), altrimenti vale 0.
Se \(A\) è un sottoinsieme della variabile aleatoria \(X\), allora denotiamo con \(P_{\pi}(A)\) la probabilità assegnata ad \(A\) dalla distribuzione \(P_{\pi}\). Mediante una distribuzione di probabilità \(P_{\pi}\) è possibile determinare la probabilità di ciascun sottoinsieme \(A \subset X\) come \[P_{\pi}(A) = \sum_{x \in A} P_{\pi}(x).\] Qui non facciamo altro che applicare il terzo assioma di Kolmogorov.
Soluzione. Per risolvere tale problema iniziamo a considerare il fatto che l’evento \(S = 7\) si verifica in corrispondenza di sei punti elementari dello spazio campionario \(\Omega\): {(1, 6), (2, 5), (3, 4), (4, 3), (2, 5), (6, 1)}. Dunque, \[\begin{equation} P(S = 7) = P\{(1, 6)\} + P\{(2, 5)\} + P\{(3, 4)\} + P\{(4, 3)\} + P\{(2, 5)\} + P\{(6, 1)\}. \end{equation}\] Se possiamo assumere che i due dadi sono bilanciati, allora ciascun evento elementare dello spazio campionario ha probabilità \(\frac{1}{36}\) e la probabilità cercata diventa \(\frac{1}{6}\). È facile estendere il ragionamento fatto sopra a tutti i valori che \(S\) può assumere. In questo modo giungiamo alla funzione di massa di probabilità \(P_0\) riportata nella prima riga della tabella seguente.
| s | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| \(P_0(S = s)\) | \(\frac{1}{36}\) | \(\frac{2}{36}\) | \(\frac{3}{36}\) | \(\frac{4}{36}\) | \(\frac{5}{36}\) | \(\frac{6}{36}\) | \(\frac{5}{36}\) | \(\frac{4}{36}\) | \(\frac{3}{36}\) | \(\frac{2}{36}\) | \(\frac{1}{36}\) |
| \(P_1(S = s)\) | \(\frac{4}{64}\) | \(\frac{4}{64}\) | \(\frac{5}{64}\) | \(\frac{6}{64}\) | \(\frac{7}{64}\) | \(\frac{12}{64}\) | \(\frac{7}{64}\) | \(\frac{6}{64}\) | \(\frac{5}{64}\) | \(\frac{4}{64}\) | \(\frac{4}{64}\) |
Per considerare un caso più generale, poniamoci ora il problema di trovare la funzione di massa di probabilità di \(S\) nel caso di due dadi truccati aventi la seguente distribuzione di probabilità: \[ \begin{aligned} P(\{1\}) = P(\{6\}) &= \frac{1}{4};\notag\\ P(\{2\}) = P(\{3\}) = P(\{4\}) = P(\{5\}) = \frac{1}{8}\notag. \label{eq:loaded_dice} \end{aligned} \] Nel caso dei due dadi truccati, la probabilità dell’evento elementare (1, 1) è 1/4 1/4. Dunque, P(S = 2) = 4/64. La probabilità dell’evento elementare (1, 2) è 1/4 1/8. Tale valore è uguale alla probabilità dell’evento elementare (2, 1). La probabilità che S sia uguale a 3 è 1/4 1/8 + 1/8 1/4 = 4/64, e così via. Svolgendo i calcoli per tutti i possibili valori di S otteniamo la funzione di massa di probabilità \(P_1\) riportata nella seconda riga della tabella precedente.
Si noti che, a partire dalla funzione di massa di probabilità di S, è possibile calcolare la probabilità di altri eventi. Per esempio, possiamo dire che l’evento S > 10 ha una probabilità minore nel caso dei dadi bilanciati, ovvero 3/36 = 1/12, rispetto al caso dei dadi truccati considerati in precedenza dove, per lo stesso evento, abbiamo una probabilità di 8/64 = 1/8.13.8 Notazione
Qui sotto è riportata la notazione che verrà usata per fare riferimento ad eventi e probabilità, nel caso discreto e continuo, in maniera tale che queste convenzioni siano elencate tutte in un posto solo.
- Gli eventi sono denotati da lettere maiuscole, es. \(A\), \(B\), \(C\).
- Una variabile aleatoria è denotata da una lettera maiuscola, ad esempio \(X\), e assume valori denotati dalla stessa lettera minuscola, ad esempio \(x\).
- La connessione tra eventi e valori viene espressa nei termini seguenti: “\(X = x\)” significa che l’evento \(X\) assume il valore \(x\).
- La probabilità di un evento è denotata con \(P(A)\).
- Una variabile aleatoria discreta ha una funzione di massa di probabilità denotata con \(p(x)\). La relazione tra \(P\) e \(p\) è che \(P(X=x) = p(x)\).
Conclusioni
In questo capitolo abbiamo visto come si costruisce lo spazio campionario di un esperimento casuale, quali sono le proprietà di base della probabilità e come si assegnano le probabilità agli eventi definiti sopra uno spazio campionario discreto. Abbiamo anche introdotto le nozioni di “variabile aleatoria” e di “funzione di massa di probabilità.” Le procedure di analisi dei dati psicologici che discuteremo in seguito faranno un grande uso di questi concetti e della notazione qui introdotta.