Capitolo 19 La funzione di verosimiglianza
Per introdurre la funzione di verosimiglianza utilizzeremo un esempio proposto da McElreath (2020) – per una trattazione più formale è possibile consultare il tutorial di Etz (2018). Supponiamo di tenere in mano un mappamondo gonfiabile e di chiederci: “qual’è la proporzione della superficie terreste ricoperta d’acqua?” Sembra una domanda a cui è difficile rispondere. Ma ci viene in mente questa idea brillante: lanciamo in aria il mappamondo e, quando lo riprendiamo, osserviamo se la superfice del mappamondo sotto il nostro dito indice destro rappresenta acqua o terra. Possiamo ripetere questa procedura più volte, così da ottenere un campione causale di diverse porzioni della superficie dal mappamondo. Eseguiamo il nostro esperimento lanciando in aria il mappamondo nove volte e osserviamo i seguenti risultati: A, T, A, A, A, T, A, T, A, dove “A” indica acqua e “T” indica terra. In questo esempio, McElreath (2020) illustra come sia possibile analizzare questi dati per stimare la proporzione della superficie del globo terrestre che è ricoperta d’acqua. Mediante questo esempio, McElreath (2020) introduce inoltre il concetto di verosimiglianza.
19.1 La narrazione dei dati
Secondo McElreath (2020) l’analisi Bayesiana può essere descritta come la produzione di una storia che viene raccontata dai dati. Lo scopo di una tale narrazione è quello di chiarire come i dati sono stati generati. Per potere formulare la narrazione dei dati è necessario descrivere le caratteristiche del mondo che ha generato il fenomeno di interesse e il processo attraverso il quale abbiamo ottenuti i dati. In altri termini, la narrazione dei dati corrisponde alla descrizione del processo di campionamento. Per l’esempio del mappamondo possiamo dire quanto segue:
- la proporzione del pianeta Terra ricoperta d’acqua è \(p\);
- un singolo lancio del mappamondo ha una probabilità \(p\) di produrre l’osservazione “acqua” (A);
- i lanci del mappamondo sono indipendenti (nel senso che il risultato di un lancio non influenza i risultati degli altri lanci).
In una tale narrazione dei dati distinguiamo i dati dai parametri. I dati sono le frequenze degli eventi \(A\) (“acqua”) e \(T\) (“terra”). La somma delle frequenze di \(A\) e \(T\) è il numero totale dei lanci del mappamondo: \(N = A + T\).
La narrazione di cui ci occupiamo fa riferimento, oltre ai dati, anche al parametro \(p\), ovvero alla proporzione di acqua sul globo terrestre. La descrizione di tale parametro rappresenta l’obiettivo dell’inferenza.
Anche se il parametro \(p\) non può essere direttamente osservato è possibile inferire il suo valore a partire dai dati. Avendo specificato ciò che abbiamo stato detto sopra, la narrazione dei dati si trasforma in un modello probabilistico – in questo caso, abbiamo una sequenza di prove Bernoulliane indipendenti e, dunque, il modello statistico è quello Binomiale. Un tale modello probabilistico è facile da costruire, e vedremo come si fa. Tuttavia, prima di descrivere questo modello probabilistico in dettaglio, è utile visualizzare il suo comportamento. Dopo aver visto come questo modello apprende dai dati ci porremo il problema di capire come funziona.
19.1.1 Come impara un modello statistico?
Prima di lanciare in aria il mappamondo e di ottenere il primo dato, non sappiamo nulla del parametro \(p\). Dato che \(p\) è una proporzione, i suoi valori possibili vanno da 0 a 1. Se non possediamo alcuna informazione su \(p\), allora riteniamo che tutti i valori \(p\) siano egualmente plausibili. Rappresentiamo dunque la nostra incertezza a proposito del parametro \(p\) mediante una distribuzione uniforme su tutti i valori \(p\), come indicato dalla linea tratteggiata nel pannello \(n = 1\) della figura 19.1.
Figura 19.1: Come apprende un modello statistico. Ciascun lancio del mappamondo produce un’osservazione: acqua (A) o terra (T). La stima del modello statistico della proporzione di acqua sulla superficie terreste è espressa nei termini del grado di plausibilità di ciascun possibile valore \(p\) (proporzione di acqua). Le linee e le curve in questa figura rappresentano il grado di plausibilità fornito dal modello. In ogni diagramma, le plausibilità calcolate in base alle informazioni precedenti (curva tratteggiata) vengono aggiornate alla luce dell’ultima osservazione che è stata ottenuta per produrre un nuovo insieme di valori di plausibilità (curva solida).
Lanciamo in aria il mappamondo una prima volta e, quando lo riprendiamo, notiamo che sotto il nostro indice destro c’è “acqua.” Dopo avere osservato il risultato del primo lancio, ovvero “A,” il modello aggiorna le plausibilità dei valori del parametro \(p\) che ora sono rappresentate dalla linea continua nel pannello \(n = 1\) della figura 19.1. La plausibilità associata all’evento \(p = 0\) è scesa esattamente a zero, l’equivalente di “impossibile.” Infatti, avendo osservato almeno un luogo sul mappamondo in cui c’è dell’acqua, possiamo dire che l’evento “non c’è acqua” (ovvero \(p = 0\)) è impossibile. Allo stesso modo, la plausibilità di \(p > 0.5\) è aumentata. Non abbiamo ancora evidenze che ci sia terra sul mappamondo, quindi le plausibilità iniziali sono state modificate per essere coerenti con questa informazione: le plausibilità associate a \(p\) aumentano passando dal valore \(p = 0\) a valore \(p = 1\), in maniera coerente con i dati che abbiamo. Il punto importante è che le evidenze disponibili fino a questo momento vengono incorporata nelle plausibilità attribuite a ciascun possibile valore \(p\). Il modello implementa questa logica in maniera automatica. Non è necessario fornire al modello alcuna istruzione per ottenere questo risultato. La teoria della probabilità svolge tutti i calcoli necessari per noi.
Lanciamo in aria il mappamondo una seconda volta e osserviamo “T.” Consideriamo dunque il pannello n = 2 della figura 19.1. La linea tratteggiata in questo pannello ricopia semplicemente la descrizione del livello di plausibilità di ciascun valore \(p\) che era disponibile nel caso di un solo lancio del mappamondo. La linea continua, invece, aggiorna tali valori di plausibilità incorporando l’informazione secondo la quale in due lanci abbiamo ottenuto “acqua” una volta e “terra” una volta. Vediamo che ora il valore di plausibilità di \(p\) è uguale a zero per l’evento \(p = 0\); infatti, abbiamo osservato “acqua” nel primo lancio. In maniera corrispondente, il valore di plausibilità di \(p\) è uguale a zero per l’evento \(p = 1\) (c’è solo acqua); infatti, abbiamo osservato “terra” nel secondo lancio. Avendo osservato “acqua” nel 50% dei casi, il valore più verosimile per \(p\) sarà 0.5, come indicato dalla linea continua in questo pannello.
Nei pannelli rimanenti della figura 19.1 i nuovi dati prodotti dai successivi lanci del mappamondo vengono analizzati dal modello, uno alla volta. La curva tratteggiata in ciascun pannello corrisponde alla curva solida del pannello precedente, spostandosi da sinistra a destra e dall’alto verso il basso. Ogni volta che si ottiene un dato A il picco della curva di plausibilità si sposta a destra, verso valori più grandi di \(p\). Ogni volta si ottiene T ci si sposta nella direzione opposta. L’altezza massima della curva aumenta con ogni campione, il che significa che, all’aumentare della quantità di prove, viene associato un livello di plausibilità maggiore ad un minor numero di valori di \(p\). Man mano che viene aggiunta una nuova osservazione, la curva che rappresenta la plausibilità dei valori \(p\) viene aggiornata in maniera coerente con tutte le osservazioni precedenti.
19.2 La funzione di verosimiglianza
Nel caso dell’esempio della figura 19.1, abbiamo visto come il grado di plausibilità che può essere associato a ciascun valore di un parametro (nel caso presente, \(p\), ovvero la proporzione di acqua sulla superficie terreste) può essere descritto mediante una curva. Una curva è il grafico di una funzione matematica. In statistica, tale funzione si chiama verosimiglianza.
19.2.1 La verosimiglianza del modello Binomiale
Nel caso dell’esperimento casuale costituito dal lancio del mappamondo, è possibile individuare la funzione di verosimiglianza utilizzando le informazioni fornite dalla narrazione dei dati. Iniziamo elencando tutti i possibili eventi che possono essere osservati nel nostro esperimento casuale. Ce ne sono due: acqua (\(A\)) e terra (\(T\)). Non ci sono altri eventi. Il mappamondo non può mai rimanere bloccato sul soffitto, per esempio. Quando osserviamo un campione di eventi \(A\) e \(T\) di lunghezza \(N\) (9 nel campione in esame qui), la domanda che ci poniamo è: quanto è probabile osservare questo preciso campione (6 volte “acqua” in 9 lanci del mappamondo) nell’universo di tutti i possibili campioni costituiti da 9 lanci del mappamondo? Potremmo pensare che questa è una domanda a cui è molto difficile rispondere, ma in realtà ciò non è vero. Se specifichiamo le caratteristiche dell’esperimento casuale come abbiamo fatto sopra, ovvero: (1) ogni lancio è indipendente dagli altri lanci e (2) la probabilità di osservare “acqua” è la stessa in ogni lancio, allora la teoria della probabilità ci consente di trovare facilmente una risposta alla nostra domanda. Le caratteristiche dell’esperimento casuale che abbiamo descritto sopra specificano le condizioni che definiscono una variabile aleatoria binomiale. La funzione che stiamo cercando, dunque, è la distribuzione binomiale. In precedenza abbiamo discusso tale distribuzione facendo riferimento all’esperimento casuale che consisteva nel “lancio di una moneta” una certo numero di volte. Ma l’esperimento casuale del lancio di una moneta è strutturalmente identico a quello del lancio del mappamondo gonfiabile dato che, nel nostro caso, gli unici esiti possibili sono “acqua” e “terra,” i lanci sono indipendenti gli uni dagli altri e se la probabilità di osservare “acqua” rimane costante in ciascun lancio. Possiamo dunque usare la distribuzione binomiale per descrivere la probabilità di osservare A = “numero di volte in cui abbiamo osservato acqua” e T = “numero di volte in cui abbiamo osservato terra,” quando il nostro mappamondo è stato lanciato in aria per N = A + T volte. Tale probabilità è data dalla distribuzione binomiale di parametro \(p\):
\[\begin{equation} P(A, T \mid p) = \frac{(A + T)!}{A!T!} p^A + (1-p)^T. \tag{19.1} \end{equation}\]
In altre parole, la frequenza degli eventi “numero di volte in cui abbiamo osservato acqua” e “numero di volte in cui abbiamo osservato terra” segue la distribuzione binomiale nella quale la probabilità di osservare “acqua” in ciascun lancio è uguale a \(p\).
19.2.2 La verosimiglianza vista da vicino
Ma cosa dobbiamo fare, in pratica, per generare le funzioni di verosimiglianza che sono rappresentate nei diversi pannelli della figura 19.1? Iniziamo con una definizione formale.
La funzione di verosimiglianza \(\mathcal{L}(\theta \mid x) = f(x \mid \theta), \theta \in \Theta,\) è la funzione di massa o di densità di probabilità dei dati \(x\) vista come una funzione del parametro sconosciuto \(\theta\).
Spesso per indicare la verosimiglianza si scrive \(\mathcal{L}(\theta)\) se è chiaro a quali valori \(x\) ci si riferisce. La verosimiglianza \(\mathcal{L}\) è una curva (in generale, una superficie) nello spazio del parametro \(\theta\) (in generale, dei parametri \(\boldsymbol\theta\)) che riflette la plausibilità relativa dei valori \(\theta\) alla luce dei dati osservati. Notiamo un punto importante. La funzione \(\mathcal{L}(\theta \mid x)\) non è una funzione di densità. Infatti, essa non racchiude un’area unitaria.
Nel caso presente, la funzione di verosimiglianza è descritta dall’eq. (19.1), ovvero, corrisponde alla funzione binomiale con parametro \(p \in (0, 1)\) sconosciuto. Nell’esempio che stiamo discutendo, abbiamo osservato “acqua” sei volte in nove lanci del mappamondo. Dunque, abbiamo \(x = 6\) successi in \(N = 9\) prove. Per i dati del campione considerato, la funzione di verosimiglianza è
\[\begin{equation} \mathcal{L}(p \mid x) = \frac{(6 + 3)!}{6!3!} p^6 + (1-p)^3. \tag{19.2} \end{equation}\]
La definizione precedente ci dice che, tenendo costanti i dati, dobbiamo applicare l’eq. (19.2) a tutti i possibili valori \(p\).
Per esempio, se \(p = 0.1\)
\[ \mathcal{L}(p \mid x) = \frac{(6 + 3)!}{6!3!} 0.1^6 + (1-0.1)^3 \] otteniamo il valore 0.0446. Se \(p = 0.2\)
\[ \mathcal{L}(p \mid x) = \frac{(6 + 3)!}{6!3!} 0.2^6 + (1-0.2)^3 \tag{19.3} \]
otteniamo 0.1762; e così via.
La tabella seguente riportata alcuni valori rappresentativi della funzione di verosimiglianza definita da 6 successi in 9 prove Bernoulliane.
| \(p\) | \(\mathcal{L}(p \mid x)\) = \({9}\choose{6}\) \(p^6 (1-p)^3\) |
|---|---|
| 0.0 | 0.0000 |
| 0.1 | 0.0001 |
| 0.2 | 0.0028 |
| 0.3 | 0.0210 |
| 0.4 | 0.0743 |
| 0.5 | 0.1641 |
| 0.6 | 0.2508 |
| 0.7 | 0.2668 |
| 0.8 | 0.1762 |
| 0.9 | 0.0446 |
| 1.0 | 0.0000 |
La figura 19.2 ci fornisce una rappresentazione grafica della funzione di verosimiglianza.
N <- 9
x <- 6
theta <- seq(0, 1, length.out=100)
like <- choose(N, x) * theta^x * (1 - theta)^(N - x)
plot(theta, like,
type='l', xaxt="n", bty = 'l',
main="Funzione di verosimiglianza",
ylab=expression(L(theta)),
xlab=expression('Valori possibili di' ~ theta))
axis(side=1, at=seq(0, 1, length.out=11))
segments(0.67, 0, 0.67, choose(N, x) * 0.67^x * (1 - 0.67)^(N - x), lty=2)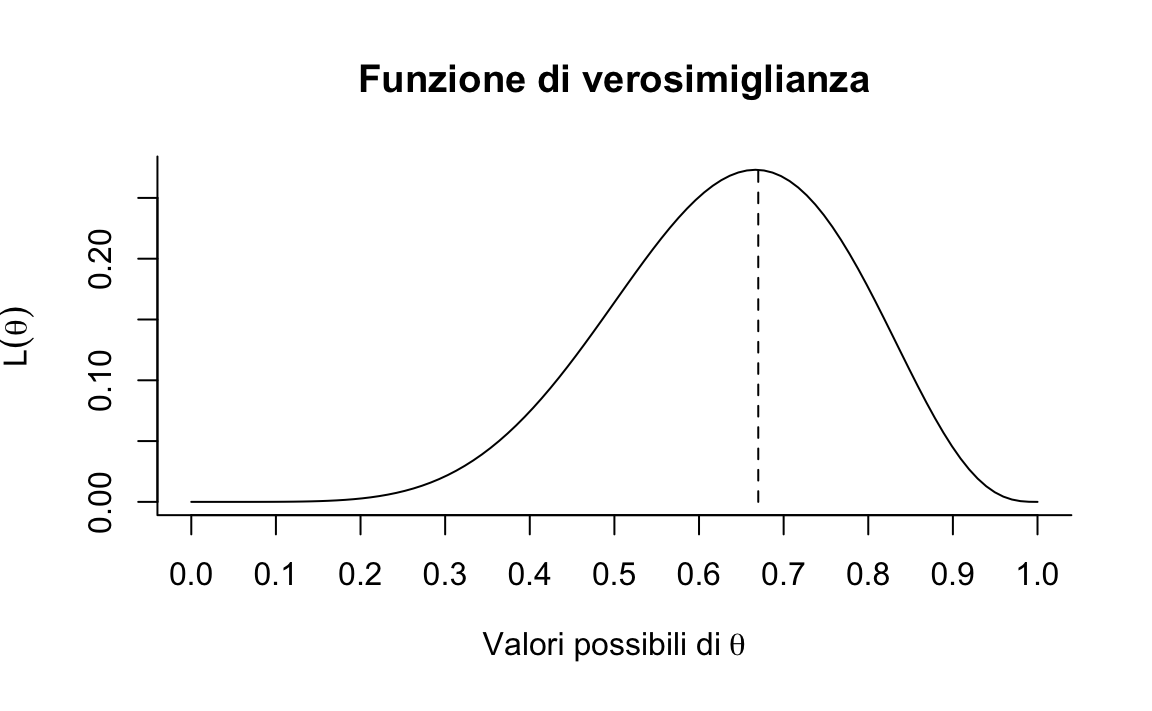
Figura 19.2: Funzione di verosimiglianza nel caso in cui l’esito acqua sia stato osservato 6 volte in 9 lanci del mappamondo.
Che cosa significano i valori che abbiamo ottenuto? Per alcuni valori \(p\) la funzione di verosimiglianza assume valori bassi; per altri valori la funzione assume valori più grandi. Questi ultimi sono dunque i valori di \(p\) “più plausibili” e il valore 0.67 è il più plausibile tra tutti. In conclusione, la funzione di verosimiglianza ci dice quanto possiamo ritenere “relativamente plausibili” i diversi valori del parametro \(p\) alla luce dei dati osservati. La figura 19.2, infatti, mostra come la funzione di verosimiglianza assume una forma diversa in presenza di campioni diversi di dati: le curve nei diversi pannelli della figura 19.1 sono sempre state ottenute mediante l’eq. (19.1), ma inserendo nella formula informazioni diverse relativamente ai dati: 1 successo in 1 prova (abbiamo lanciato il mappamondo una volta e abbiamo osservato “acqua”); 1 successo in 2 prove (abbiamo lanciato il mappamondo due volte e abbiamo osservato “acqua” e “terra”); 2 successi in 3 prove (abbiamo lanciato il mappamondo tre volte e abbiamo osservato “acqua,” “terra” e “acqua”); eccetera.
19.2.3 La stima di massima verosimiglianza
La funzione di verosimiglianza rappresenta la “verosimiglianza relativa” dei diversi valori del parametro di interesse. Ma qual è il valore migliore di tutti?
A questa domanda si può rispondere in due modi diversi.
La stima di massima verosimiglianza \(\hat{\theta}_{ML}\) di un parametro \(\theta\) si ottiene massimizzando la funzione di verosimiglianza:
\[ \hat{\theta}_{ML} = \text{argmax}_{\theta \in \Theta} \mathcal{L}(\theta). \] L’approccio frequentista, diversamente da quello Bayesiano, utilizza la funzione di verosimiglianza quale unico strumento per giungere alla stima del valore più plausibile del parametro sconosciuto \(p\) nel caso dell’esempio del mappamondo – in generale, possiamo chiamare \(\theta\) il parametro sconosciuto. Il metodo della massima verosimiglianza consiste nel trovare il valore \(\theta\) che più verosimilmente ha generato i dati. Tale stima corrisponde al punto di massimo della funzione di verosimiglianza. Nell’esempio presente, \(\hat{p}_{ML} = 0.6667\). Nell’esempio che abbiamo discusso, il massimo della funzione di verosimiglianza, ovvero la stima di \(p\), si può facilmente ottenere con metodi numerici o grafici.
19.2.4 La log-verosimiglianza
Per motivi algebrici e numerici è conveniente lavorare con il logaritmo della funzione di verosimiglianza, che viene chiamata funzione di log-verosimiglianza,
\[ \ell(\theta) = \log \mathcal{L}(\theta).\notag \]
Poiché il logaritmo è una funzione strettamente crescente (usualmente si considera il logaritmo naturale), allora \(\mathcal{L}(\theta)\) e \(\ell(\theta)\) assumono il massimo (o i punti di massimo) in corrispondenza degli stessi valori di \(\theta\):
\[ \hat{\theta}_{ML} = \text{argmax}_{\theta \in \Theta} \ell(\theta). \] Per le proprietà del logaritmo, si ha
\[ \ell(\theta) = \log \left( \prod_{i = 1}^n f(x \mid \theta) \right) = \sum_{i = 1}^n \log f(x \mid \theta). \]
Si noti che non è necessario lavorare con i logaritmi, anche se è fortemente consigliato, e questo perché i valori della verosimiglianza, in cui si moltiplicano valori di probabilità molto piccoli, possono diventare estremamente piccoli (qualcosa come \(10^{-34}\)). In tali circostanze, non è sorprendente che i programmi dei computer mostrino problemi di arrotondamento numerico. Le trasformazioni logaritmiche risolvono questo problema.
19.2.5 Derivazione della massima verosimiglianza
Nell’esempio precedente abbiamo trovato che la stima di massima verosimiglianza di \(p\) è uguale alla proporzione di successi campionari. Questo risultato può essere dimostrato come segue. Per \(N\) prove Bernoulliane indipendenti, le quali producono \(x\) successi e (\(N-x\)) insuccessi, la funzione nucleo (ovvero, la funzione di verosimiglianza da cui sono state escluse tutte le costanti moltiplicative, dato che esse non hanno alcun effetto su \(\hat{p}_{ML}\)) è
\[ \mathcal{L}(p \mid x) = p^x (1-p)^{N - x}.\notag \]
La funzione nucleo di log-verosimiglianza è
\[ \begin{aligned} \ell(p \mid x) &= \log \mathcal{L}(p \mid x) \notag\\ &= \log \left( p^x (1-p)^{N - x} \right) \notag\\ &= \log p^x + \log \left( (1-p)^{N - x} \right) \notag\\ &= x \log p + (N - x) \log (1-p).\notag\end{aligned} \]
Per calcolare il massimo della funzione di log-verosimiglianza è necessario differenziare \(\ell(p \mid x)\) rispetto a \(p\), porre la derivata a zero e risolvere. La derivata di \(\ell(p \mid x)\) è:
\[ \ell'(p \mid x) = \frac{x}{p} -\frac{N-x}{1-p}. \]
Ponendo l’equazione uguale a zero e risolvendo otteniamo la stima di massima verosimiglianza:
\[\begin{equation} \hat{p}_{\text{ML}} = \frac{x}{N}, \tag{19.4} \end{equation}\]
ovvero la frequenza relativa dei successi nel campione.
19.2.6 Calcolo numerico
La derivazione formale del risultato secondo il quale la stima di massima verosimiglianza corrisponde alla proporzione di successi nel campione è piuttosto complessa. Lo stesso risultato può essere ottenuto in maniera molto più semplice mediante una simulazione svolta in R. A questo fine, iniziamo con il definire una serie di valori possibili per il parametro incognito \(p\):
p <- seq(0, 1, length.out=1e3)Sappiamo che la funzione di verosimiglianza è la funzione di massa di probabilità espressa in funzione del parametro sconosciuto \(p\) e assumendo come noti i dati. Questo si può esprimere in ne modo seguente:
like <- dbinom(6, 9, p)Si noti che, nell’istruzione precedente, abbiamo passato alla funzione
dbinom() i dati, ovvero 6 successi in 9 prove. Inoltre, abbiamo
passato alla funzione un vettore che contiene 1000 valori possibili per
il parametro \(p\), da 0 a 1. Per ciascuno di questi valori di \(p\), la
funzione dbinom() ci ritorna un valore (cioè l’ordinata della funzione
di verosimiglianza), tenendo costanti in tutti i casi i valori dei dati
(ovvero, 6 successi in 9 prove). Un grafico della funzione di
verosimiglianza è dato da:
plot(p, like, type='l')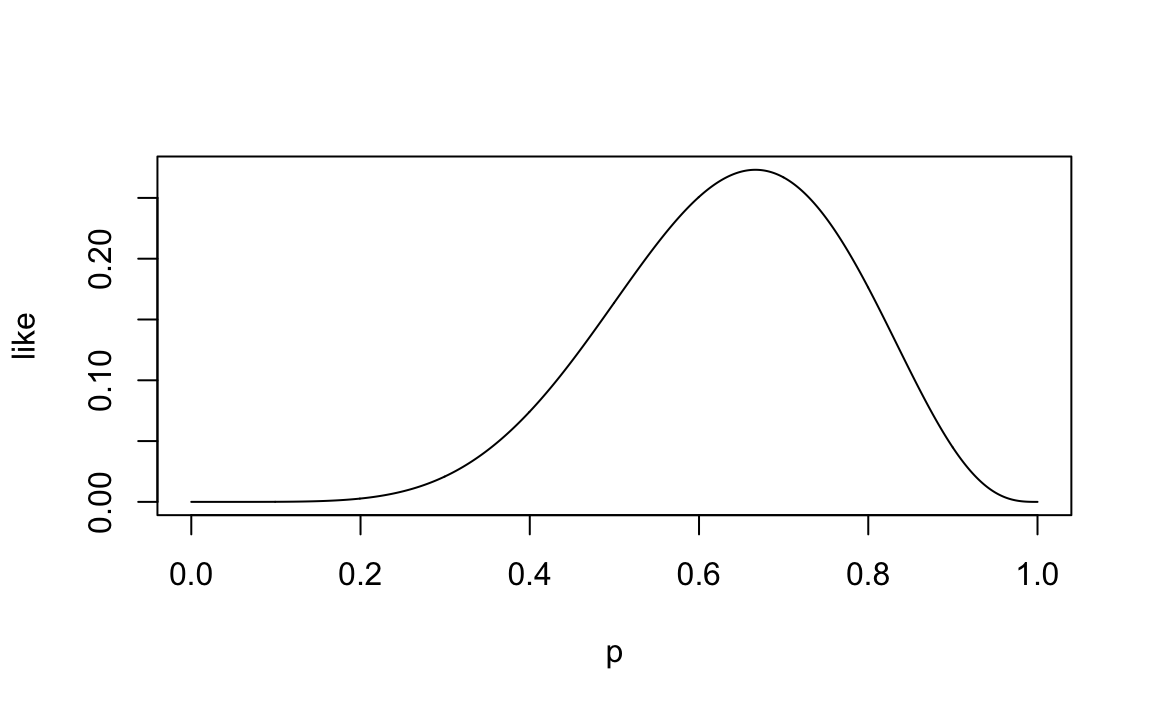
Nella simulazione, il valore \(p\) che massimizza la funzione di verosimiglianza può essere trovato nel modo seguente:
p[which.max(like)]
#> [1] 0.6666667Si noti come il valore trovato sia uguale al valore definito dall’eq. (19.4).
19.3 La verosimiglianza del modello Normale
Ora che abbiamo capito come si definisce la funzione verosimiglianza di una Binomiale è relativamente semplice fare un passo ulteriore e considerare la verosimiglianza del caso di una funzione di densità, ovvero nel caso di una variabile aleatoria continua. Consideriamo qui il caso della Normale. La densità di una distribuzione Normale di parametri \(\mu\) e \(\sigma\) è
\[ f(x \mid \mu, \sigma) = \frac{1}{\sigma \sqrt{2\pi}} \exp\left\{-\frac{1}{2\sigma^2}(x-\mu)^2\right\}. \tag{19.5} \]
Per un campione i.i.d. \(\mathscr{D}_n = x_1, x_2, \dots, x_n\) con densità Normale di parametri \(\mu\) e \(\sigma\), poniamoci il problema di trovare la stima di massima verosimiglianza dei parametri sconosciuti \(\mu\) e \(\sigma\). Per semplicità, scriviamo \(\theta = \{\mu, \sigma\}.\)
In precedenza abbiamo utilizzato la nozione di probabilità congiunta per fare riferimento alla probabilità del verificarsi di un insieme di eventi. Estendiamo questo ragionamento al caso presente.
Consideriamo il campione osservato come un insieme di eventi. Ciascuno di tali eventi è la realizzazione di una variabile aleatoria (possiamo pensarla come l’estrazione casuale di un valore dalla “popolazione” \(\mathcal{N}(\mu, \sigma)\)). Tali variabili aleatorie sono mutualmente indipendenti, tutte con la stessa legge distributiva, e la densità congiunta è data da:
\[ \begin{aligned} f(\mathscr{D}_n \mid \theta) &= f(x_1 \mid \theta) \cdot f(x_2 \mid \theta) \cdot \dots \cdot f(x_n \mid \theta)\notag\\ &= \prod_{i=1}^n f(x_i \mid \theta), \end{aligned} \]
laddove la funzione \(f(\cdot)\) è data dall’eq. (19.5). L’associata funzione di verosimiglianza è dunque:
\[\begin{equation} \mathcal{L}(\theta \mid \mathscr{D}_n) = \prod_{i=1}^n f(x_i \mid \theta). \tag{19.6} \end{equation}\]
L’obiettivo è massimizzare la funzione di verosimiglianza per trovare i valori \(\theta\) ottimali. Usando la notazione matematica questo si esprime dicendo che cerchiamo l’argmax dell’eq. (19.6) rispetto a \(\theta\), ovvero
\[ \hat{\theta}_{\text{MLE}} = \text{argmax}_{\theta} \prod_{i=1}^n f(x_i \mid \theta). \]
In termini formali, questo problema si risolve calcolando le derivate della funzione rispetto a \(\theta\), ponendo le derivate uguali a zero e risolvendo. Saltando tutti i passaggi algebrici di questo procedimento, per \(\mu\) troviamo che
\[\begin{equation} \hat{\mu}_{\text{MLE}} = \frac{1}{n} \sum_{i=1}^n x_i \tag{19.7} \end{equation}\]
e per \(\sigma\) abbiamo
\[\begin{equation} \hat{\sigma}_{\text{MLE}} = \sqrt{\sum_{i=1}^n\frac{1}{n}(x_i- \mu)^2}. \tag{19.8} \end{equation}\]
In altri termini, la stima di massima verosimiglianza per il parametro \(\mu\) è la media del campione e la stima di massima verosimiglianza per il parametro \(\sigma\) è la deviazione standard del campione.
19.3.1 Simulazione
Consideriamo ora un esempio relativo al campione di valori BDI-II dei trenta soggetti del campione clinico descritto da Zetsche et al. (2019), ovvero
d <- data.frame(x = c(26, 35, 30, 25, 44, 30, 33, 43, 22, 43, 24, 19, 39, 31, 25, 28, 35, 30, 26, 31, 41, 36, 26, 35, 33, 28, 27, 34, 27, 22))Ci poniamo lo scopo di generare la funzione di verosimiglianza per questi dati. Supponiamo che ricerche precedenti ci dicano che il BDI-II si distribuisce secondo una legge Normale.
Ci concentriamo qui sul parametro \(\mu\) della distribuzione Normale. Per semplificare il problema, assumiamo di conoscere \(\sigma\) (lo porremo uguale alla deviazione standard del campione), in modo da avere un solo parametro sconosciuto. Il nostro problema è dunque quello di trovare la funzione di verosimiglianza per il parametro \(\mu\), date le 30 osservazioni che abbiamo a disposizione.
Abbiamo visto sopra che, per una singola osservazione, la funzione di verosimiglianza è la densità Normale espressa in funzione dei parametri. Nel caso di un campione di osservazioni \(\mathscr{D}_n = (x_1, x_2, \dots, x_n)\) dobbiamo utilizzare la funzione di densità congiunta \(f(\mathscr{D}_n \mid \mu, \sigma)\) espressa in funzione dei parametri, ovvero \(\mathcal{L}(\mu, \sigma \mid \mathscr{D}_n)\). Se le 30 osservazioni sono i.i.d., allora la densità congiunta è data dal prodotto della densità di ciascuna singola osservazione. Per una singola osservazione \(x_i\) abbiamo
\[ f(x_i \mid \mu, \sigma) = \frac{1}{{\sigma \sqrt {2\pi}}}\exp\left\{{-\frac{(x_i - \mu)^2}{2\sigma^2}}\right\},\notag \]
dove il pedice \(i\) specifica la singola osservazione \(x_i\) tra le molteplici osservazioni \(x\), e \(\mu\) e \(\sigma\) sono i parametri sconosciuti che devono essere determinati. La densità congiunta è dunque
\[ f(\mathscr{D}_n \mid \mu, \sigma) = \, \prod_{i=1}^n f(x_i \mid \mu, \sigma)\notag \]
e, alla luce dei dati osservati, l’associata verosimiglianza diventa
\[ \begin{aligned} \mathcal{L}(\mu, \sigma \mid \mathscr{D}_n) =& \, \prod_{i=1}^n f(x_i \mid \mu, \sigma) = \notag\\ & \frac{1}{{\sigma \sqrt {2\pi}}}\exp\left\{{-\frac{(26 - \mu)^2}{2\sigma^2}}\right\} \times \notag\\ & \frac{1}{{\sigma \sqrt {2\pi}}}\exp\left\{{-\frac{(35 - \mu)^2}{2\sigma^2}}\right\} \times \notag\\ & \vdots \notag\\ & \frac{1}{{\sigma \sqrt {2\pi}}}\exp\left\{{-\frac{(22 - \mu)^2}{2\sigma^2}}\right\}. \end{aligned} \tag{19.9} \]
Poniamoci il problema di rappresentare graficamente tale funzione di verosimiglianza per il parametro \(\mu\). Per semplicità, supponiamo che \(\sigma\) sia noto e uguale alla deviazione standard del campione.
true_sigma <- sd(d$x)Avendo un solo parametro sconosciuto da stimare possiamo rappresentare la verosimiglianza con una curva, anziché con una superficie. In R, possiamo definire la funzione di log-verosimiglianza nel modo seguente:
Si noti che, nella funzione log_likelihood, x è un vettore che, nel caso presente conterrà \(n = 30\) valori. Per ciascuno di questi valori, la funzione dnorm() troverà la densità Normale (l’ordinata della funzione) utilizzando il valore \(\mu\) che viene passato a log_likelihood e un valore \(\sigma\) sempre uguale, dato che, nell’esempio, questo parametro verrà mantenuto costante. L’argomento log = TRUE specifica che deve essere preso il logaritmo. La funzione dnorm() è un argomento della funzione sum(). Ciò significa che i 30 valori così trovati, espressi su scala logaritmica, verranno sommati. Sommare logaritmi è equivalente a fare il prodotto dei valori sulla scala originaria.
Se applichiamo questa funzione ad un solo valore \(\mu\) otteniamo un singolo valore della
funzione di log-verosimiglianza (ovvero, l’ordinata di un singolo punto della funzione rappresentata nella figura (19.9)). Ripeto, tale singolo valore viene trovato utilizzando tutti i 30 dati del campione, il valore \(\sigma = s\) che viene tenuto fisso e il singolo valore \(\mu\) che abbiamo passato alla funzione
log_likelihood(). Dobbiamo, tuttavia, applicare la funzione a tutti i possibili valori che \(\mu\) può assumere. Per cui il procedimento che abbiamo descritto per un singolo valore \(\mu\) viene ripetuto tante volte.
Nel seguente ciclo for() usato nelle istruzioni seguenti viene calcolata la log-verosimiglianza di 100000 possibili valori per il parametro \(\mu\):
nrep <- 1e5
mu <- seq(
mean(d$x) - sd(d$x),
mean(d$x) + sd(d$x),
length.out = nrep
)
ll <- rep(NA, nrep)
for (i in 1:nrep) {
ll[i] <- log_likelihood(d$x, mu[i], true_sigma)
}Il vettore mu contiene 100000 possibili valori del parametro \(\mu\). Tali valori sono stati scelti in modo tale da essere compresi nell’intervallo \(\bar{x} \pm s\).
Per ciascuno dei possibili valori del parametro \(\mu\) la funzione log_likelihood() calcola la log-verosimiglianza seguendo la procedura descritta sopra. All’interno del ciclo for() i 100000 risultati così ottenuti vengono salvati nel vettore ll.
Possiamo ora utilizzare i valori contenuti nei vettori mu e ll per disegnare il grafico della funzione di log-verosimiglianza del parametro \(\mu\):
data.frame(mu, ll) %>%
ggplot(aes(x=mu, y=ll)) +
geom_line() +
vline_at(mean(d$x), color="red", linetype="dashed") +
labs(
y="Log-verosimiglianza",
x=c("Parametro \u03BC")
) 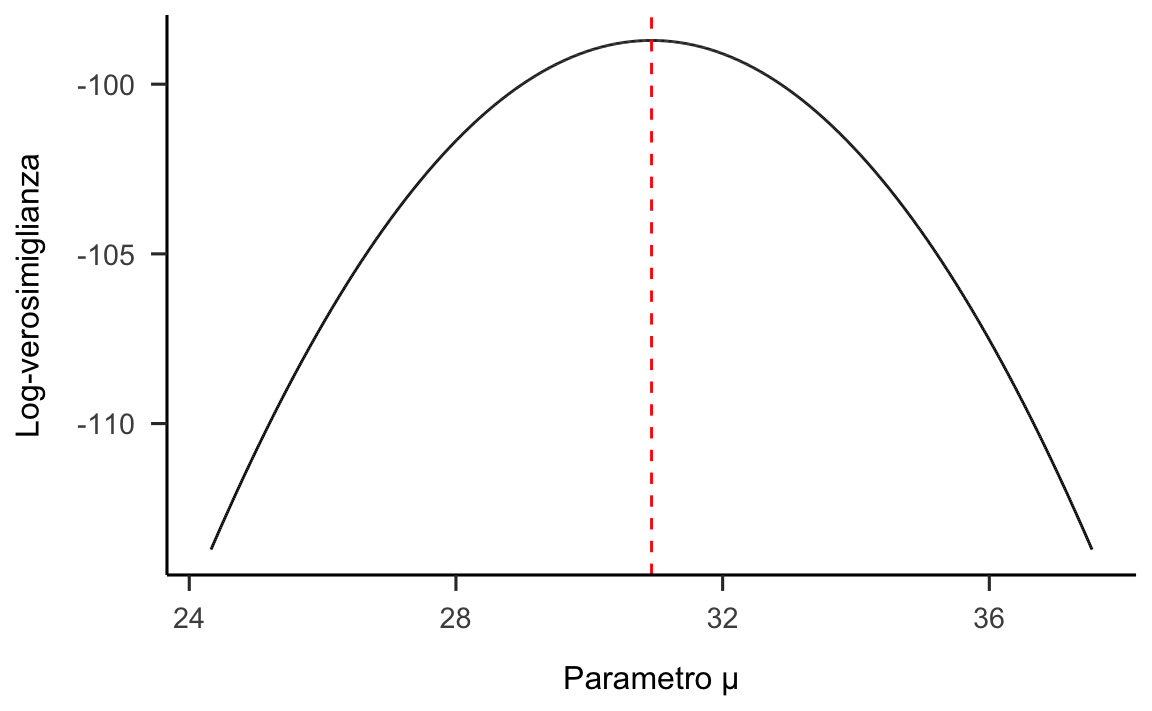
Dalla figura notiamo che, per questi dati, il massimo della funzione di log-verosimiglianza calcolata per via numerica è pari a 30.93. Tale valore è identico alla media dei dati campionari e corrisponde al risultato teorico dell’eq. (19.9).
Conclusioni
La verosimiglianza viene utilizzata sia nell’inferenza bayesiana che in quella frequentista. In entrambi i paradigmi di inferenza, il suo ruolo è quantificare la forza con la quale i dati osservati supportano i possibili valori dei parametri sconosciuti.
Nella funzione di verosimiglianza i dati (osservati) vengono trattati come fissi, mentre i valori del parametro (o dei parametri) \(\theta\) vengono variati: la verosimiglianza è una funzione di \(\theta\) per il dato fisso \(x\). Pertanto, la funzione di verosimiglianza riassume i seguenti elementi: un modello statistico che genera stocasticamente i dati (in questo capitolo abbiamo esaminato due modelli statistici: quello Binomiale e quello Normale), un intervallo di valori possibili per \(\theta\) e i dati osservati \(x\).
Nella statistica frequentista l’inferenza si basa solo sui dati a disposizione e qualunque informazione fornita dalle conoscenze precedenti non viene presa in considerazione. Nello specifico, nella statistica frequentista l’inferenza viene condotta massimizzando la funzione di (log) verosimiglianza, condizionatamente ai valori assunti dalle variabili aleatorie campionarie. Nella statistica bayesiana, invece, l’inferenza statistica viene condotta combinando la funzione di verosimiglianza con le distribuzioni a priori dei parametri incogniti \(\theta\).
La differenza fondamentale tra inferenza bayesiana e frequentista è dunque che i frequentisti non ritengono utile descrivere in termini probabilistici i parametri: i parametri dei modelli statistici vengono concepiti come fissi ma sconosciuti. Nell’inferenza bayesiana, invece, i parametri sconosciuti sono intesi come delle variabili aleatorie e ciò consente di quantificare in termini probabilistici il nostro grado di intertezza relativamente al loro valore.