19.4 Parametri e statistiche

In statistica, per popolazione si intende un insieme di elementi che presenta caratteristiche aleatorie, mentre per campione si intende un sottoinsieme della popolazione. Ma a cosa corrisponde in pratica la popolazione? Per uno psicologo la popolazione è un gruppo di individui. Per un biologo marino la popolazione è un gruppo di delfini, ad esempio. Nella maggior parte dei casi, le popolazioni oggetto di interesse per i ricercatori sono insiemi di entità concrete che esistono nel mondo reale. Dal punto di vista della statistica, invece, le popolazioni sono delle entità astratte. Infatti, gli statistici operazionalizzano il concetto di “popolazione” nei termini di un oggetto matematico che consente di essere manipolato con facilità. In precedenza noi abbiamo già incontrato questi oggetti matematici: sono le distribuzioni di probabilità.

L’idea è semplice. Supponiamo di occuparci del quoziente di intelligenza, QI. Abbiamo detto che, per uno psicologo, la popolazione di interesse solitamente è un gruppo di individui, ciascuno dei quali è dotato di uno specifico punteggio del QI. Uno statistico “semplifica” tale situazione definendo in maniera operativa la popolazione come la distribuzione di densità rappresentata nella figura 19.3. In precedenza abbiamo visto infatti come una distribuzione di densità non sia altro che la descrizione matematica della “forma” di un istogramma che rappresenta un numero molto alto di osservazioni.

library("ggfortify")
ggdistribution(dnorm, seq(60, 140, 0.1), mean = 100, sd = 15) +
  labs(
    x = "Quoziente d'intelligenza",
    y = "Densità di probabilità"
  )

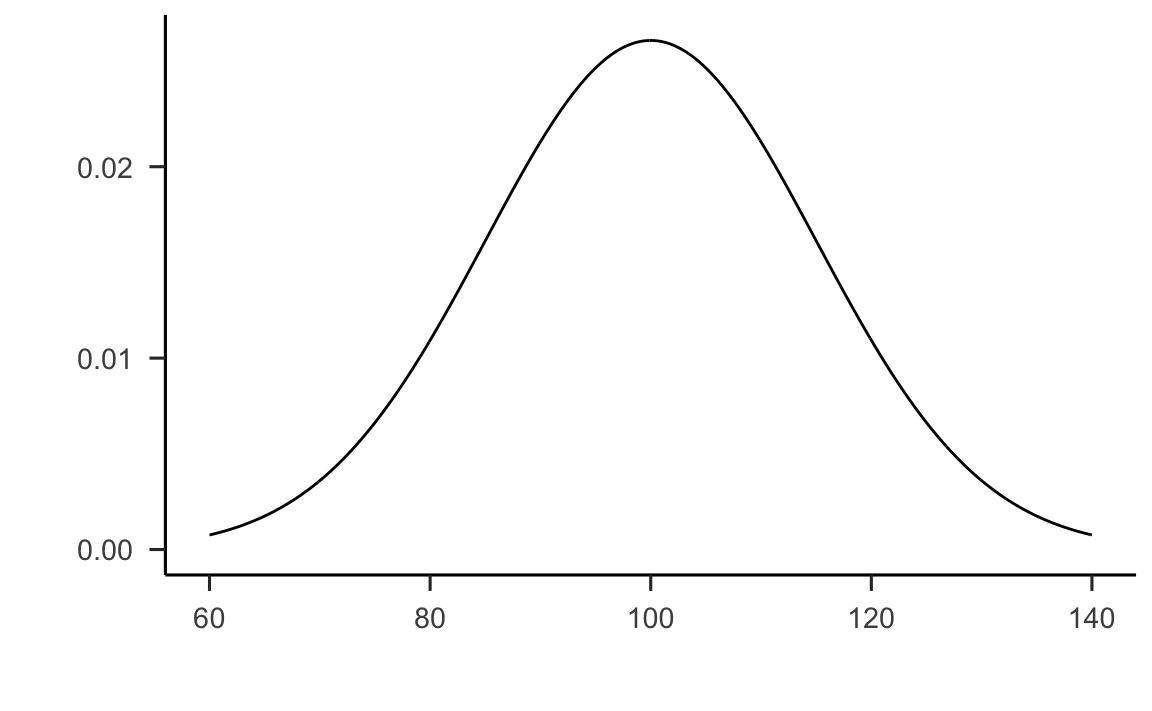
Figura 19.3: Grafico della distribuzione dei punteggi del QI nella popolazione.

I test di intelligenza sono progettati in modo che il QI medio sia pari a 100, la deviazione standard dei punteggi QI sia uguale a 15 e la distribuzione dei punteggi del QI sia normale. I valori riportati sopra sono detti parametri in quanto descrivono le proprietà dell’intera popolazione. Cioè, diciamo che la media della popolazione è \(\mu = 100\) e la deviazione standard della popolazione è \(\sigma = 15\). Dal punto di vista statistico, dunque, possiamo rappresentare questa ipotetica popolazione di valori del QI mediante l’oggetto matematico che corrisponde a una particolare distribuzione Normale:

\[ QI \sim \mathcal{N}(\mu = 100, \sigma = 15). \] Supponiamo ora di eseguire un esperimento nel quale il test di intelligenza viene somministrato a 100 persone selezionate a caso. Tale campione casuale semplice consiste nel seguente insieme di 100 numeri:

set.seed(123)
iq1 <- rnorm(100, 100, 15)
# i valori QI sono numeri interi!
iq1 <- round(iq1) 
iq1
#>   [1]  92  97 123 101 102 126 107  81  90  93 118 105 106 102  92 127 107  71 111  93  84  97
#>  [23]  85  89  91  75 113 102  83 119 106  96 113 113 112 110 108  99  95  94  90  97  81 133
#>  [45] 118  83  94  93 112  99 104 100  99 121  97 123  77 109 102 103 106  92  95  85  84 105
#>  [67] 107 101 114 131  93  65 115  89  90 115  96  82 103  98 100 106  94 110  97 105 116 107
#>  [89]  95 117 115 108 104  91 120  91 133 123  96  85

Tali valori sono stati trovati utilizzando la funzione rnorm() che genera numeri casuali estratti da una distribuzione normale. Nello specifico, abbiamo estratto 100 valori casuali dalla distribuzione normale con media 100 e deviazione standard 15. Se costruiamo un istogramma con i dati di un tale campione otteniamo il grafico mostrato nella figura 19.4.

data.frame(iq1) %>% 
  ggplot(aes(x = iq1)) +
  geom_histogram(aes(y = ..density..)) +
  labs(
    x = "Quoziente d'intelligenza",
    y = "Densità"
  )
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.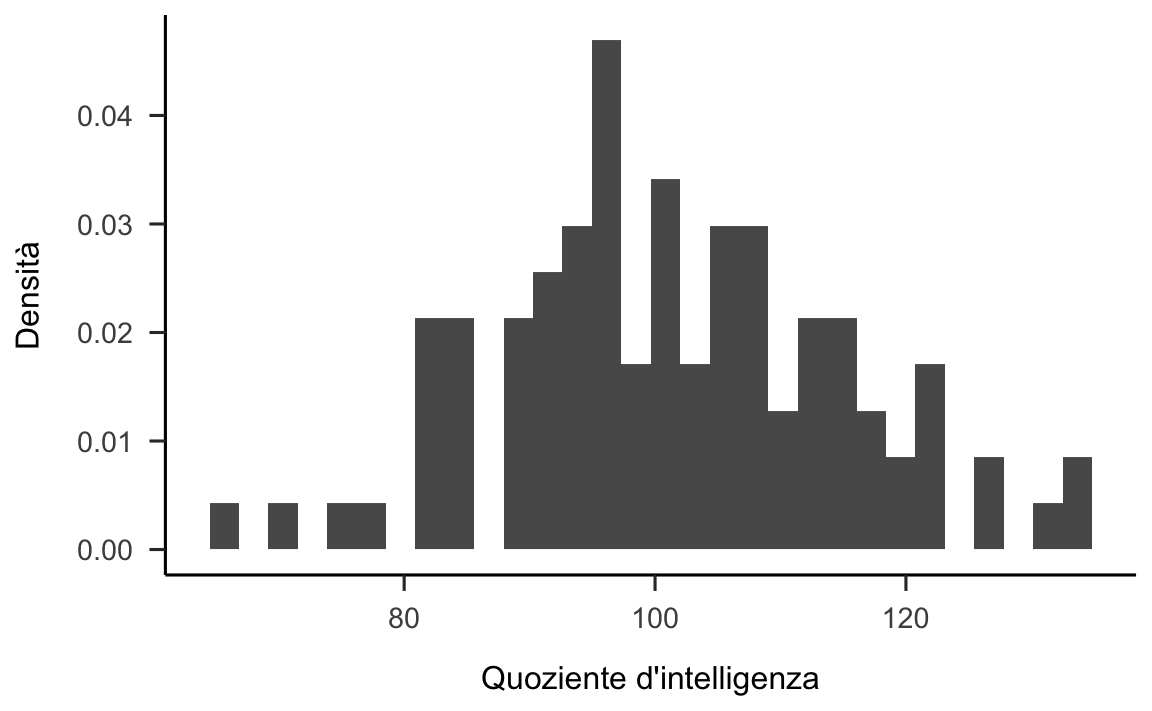

Figura 19.4: Istogramma della distribuzione dei punteggi del QI in un campione di 100 osservazioni.

Come possiamo vedere, l’istogramma ha approssimativamente la forma corretta, ma è un’approssimazione molto cruda della distribuzione della popolazione mostrata nella figura 19.3. Se calcoliamo la media del campione, otteniamo un numero abbastanza vicino alla media della popolazione di 100, ma non identico: nel campione considerato la media e la deviazione standard sono uguali a:

mean(iq1)
#> [1] 101.42
sd(iq1)
#> [1] 13.66643

Queste statistiche campionarie descrivono le proprietà di uno specifico campione che è stato osservato e, sebbene siano abbastanza simili ai parametri della popolazione, non sono uguali ad essi. In generale, le statistiche campionarie sono ciò che è possibile calcolare a partire dai dati osservati sul campione mentre i parametri della popolazione sono ciò che vorremmo conoscere.

19.5 La legge dei grandi numeri

Nella sezione Parametri e statistiche abbiamo considerato i risultati di un esperimento casuale nel quale sono stati osservati i valori fittizi del QI di un campione di ampiezza \(n = 100\). I risultati sono incoraggianti: la media campionaria di 101.42 ci fornisce un’approssimazione ragionevole della media della popolazione \(\mu = 100\). In molti studi un tale livello di precisione è accettabile, ma in altre situazioni è necessario essere più precisi.

Cosa dobbiamo fare se vogliamo che le statistiche campionarie siano più vicine ai parametri della popolazione? La risposta è ovvia: dobbiamo raccogliere più dati. Supponiamo dunque di condurre un nuovo esperimento nel quale misuriamo il QI di 10000 persone. Possiamo simulare i risultati di questo esperimento usando R:

set.seed(123)
iq2 <- rnorm(n = 10000, mean = 100, sd = 15) 
iq2 <- round(iq2) 
head(iq2)
#> [1]  92  97 123 101 102 126

Nella figura 19.5 è riportato l’istogramma dei valori del QI di questo campione più numeroso. È chiaro che, in questo secondo caso, otteniamo un’approssimazione migliore rispetto al precedente campione più piccolo. Ciò si riflette anche nelle statistiche del campione:

mean(iq2)
#> [1] 99.9671
sd(iq2)
#> [1] 14.9855

Questi valori sono molto vicini ai parametri della popolazione.

data.frame(iq2) %>% 
  ggplot(aes(x = iq2)) +
  geom_histogram(aes(y = ..density..)) +
  labs(
    x = "Quoziente d'intelligenza",
    y = "Densità"
  )
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.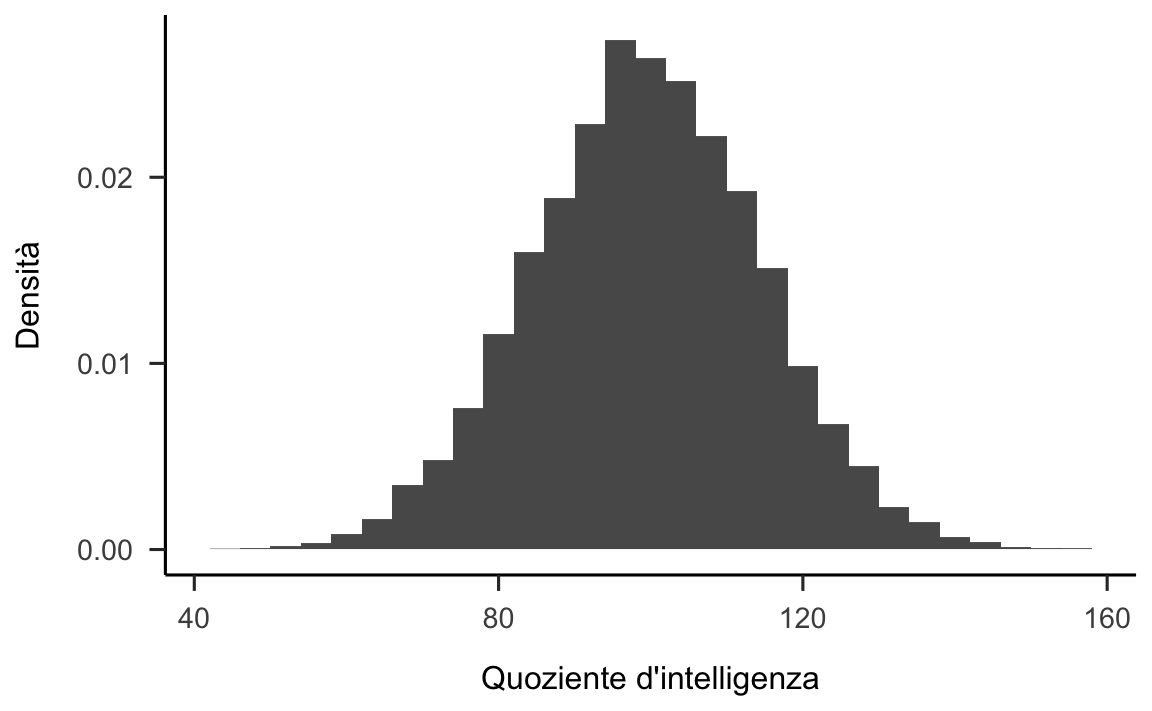

Figura 19.5: Istogramma della distribuzione dei punteggi del QI in un campione di 10000 osservazioni.

Il messaggio, un po’ banale, che ricaviamo a questa simulazione è che, generalmente, i campioni di dimensioni maggiori forniscono informazioni migliori. Ho chiamato “banali” i risultati di questa simulazione perché dovrebbe essere evidente a tutti che le cose stanno così. Infatti, questo punto è talmente ovvio che, quando Jacob Bernoulli – uno dei fondatori della teoria della probabilità – formalizzò questa idea nel 1713, commentò il risultato nel modo seguente:

Perché anche il più stupido degli uomini, basandosi soltanto sul suo istinto, da solo e senza alcuna istruzione (il che è notevole), è convinto che maggiore è il numero di osservazioni, minore è il pericolo di sbagliare.

In statistica questa intuizione va sotto il nome di Legge dei grandi numeri. La Legge dei grandi numeri ci dice che la media aritmetica di un campione di \(n\) osservazioni (in termini tecnici: di \(n\) variabili aleatorie \(X_i\) indipendenti e identicamente distribuite), ovvero \(\frac{1}{n}\sum_{i=1}^nX_i\), per \(n\) crescente tende o converge al valore atteso teorico \(\mu\). La Legge dei grandi numeri è uno degli strumenti più importanti della statistica.