Capitolo 12 Statistica descrittiva
Nel 1907 Francis Galton, cugino di Charles Darwin, matematico e statistico autodidatta, geografo, esploratore, teorico della dattiloscopia (ovvero, dell’uso delle impronte digitali a fini identificativi) e dell’eugenetica, scrisse una lettera alla rivista scientifica Nature sulla sua visita alla Fat Stock and Poultry Exhibition di Plymouth. Lì vide alcuni membri del pubblico partecipare ad un gioco il cui scopo era quello di indovinare il peso della carcassa di un grande bue che era appena stato scuoiato. Galton si procurò i 787 dei biglietti che erano stati compilati dal pubblico e considerò il valore medio di 547 kg come la “scelta democratica” dei partecipanti, in quanto “ogni altra stima era stata giudicata troppo alta o troppo bassa dalla maggioranza dei votanti.” Il punto interessante è che il peso corretto di 543 kg si dimostrò essere molto simile alla “scelta democratica” basata sulle stime dei 787 partecipanti. Galton intitolò la sua lettera a Nature Vox Populi (voce del popolo), ma questo processo decisionale è ora meglio conosciuto come la “saggezza delle folle” (wisdom of crowds). Possiamo dire che, nel suo articolo del 1907, Galton effettuò quello che ora chiamiamo un riepilogo dei dati, ovvero calcolò un indice sintetico a partire da un insieme di dati. In questo capitolo esamineremo le tecniche che sono state sviluppate nel secolo successivo per riassumere le grandi masse di dati con cui sempre più spesso ci dobbiamo confrontare. Vedremo come calcolare e interpretare gli indici di posizione e di dispersione, discuteremo le distribuzioni di frequenze e le relazioni tra variabili. Vedremo inoltre quali sono le tecniche di visualizzazione che ci consentono di rappresentare questi sommari dei dati mediante dei grafici. Ma prima di entrare nei dettagli, prendiamoci un momento per capire perché abbiamo bisogno della statistica e, per ciò che stiamo discutendo qui, della statistica descrittiva.
Ma in generale, che cos’è la statistica? Esistono molti modi per definire la statistica. Fondamentalmente, la statistica è un insieme di tecniche che ci consentono di dare un senso al mondo attraverso i dati. Ciò avviene tramite il processo di analisi statistica. L’analisi statistica traduce le domande che abbiamo a proposito del mondo in modelli matematici, utilizza i dati per scegliere i modelli matematici che sono apppropriati per descrivere il mondo e, infine, applica tali modelli per trovare una risposta alle domande che ci siamo posti. La statistica consente quindi di collegare le nostre domande a proposito del mondo ai dati, di utilizzare i dati per trovare le risposte alle domande che ci siamo posti e di valutare l’impatto delle risposte trovate.
Inizieremo la nostra discussione sulla Data Science esaminando la statistica descrittiva. Iniziamo con la statistica descrittiva non solo perché è la più facile da capire, ma anche perché essa ci fornisce gli strumenti che devono essere usati per primi in un qualsiasi progetto di analisi statistica. Nello specifico, la statistica descrittiva è un insieme di tecniche che possono essere usare per trasformare grandi (o piccole) masse di dati in indici sintetici. Tali indici sintecici ci consentono di capire le caratteristiche del mondo che sono riflesse nei dati, mentre ciò non è possibile se esaminiamo direttamente i dati grezzi.
12.1 Riassumere i dati
Quando riassumiamo i dati, necessariamente buttiamo via delle informazioni. Ma è una buona idea procedere in questo modo? Non sarebbe meglio conservare le informazioni specifiche di ciascun soggetto che partecipa ad un esperimento psicologico, al di là di ciò che viene trasmesso dagli indici riassuntivi della statistica descrittiva? Che dire delle informazioni che descrivono come sono stati raccolti i dati, come l’ora del giorno o l’umore del partecipante? Tutte queste informazioni vengono perdute quando riassumiamo i dati. La risposta alla domanda che ci siamo posti è che, in generale, non è una buona idea conservare tutti i dettagli di ciò che sappiamo. È molto più utile riassumere le informazioni perché la semplificazione risultante consente i processi di generalizzazione.
In un contesto letterario, l’importanza della generalizzazione è stata sottolineata da Jorge Luis Borges nel suo racconto “Funes o della memoria,” che descrive un individuo che perde la capacità di dimenticare. Borges si concentra sulla relazione tra generalizzazione e pensiero:
Pensare è dimenticare una differenza, generalizzare, astrarre. Nel mondo troppo pieno di Funes, c’erano solo dettagli.
Come possiamo ben capire, la vita di Funes non è facile. Se facciamo riferimento alla psicologia possiamo dire che gli psicologi hanno studiato a lungo l’utilità della generalizzazione per il pensiero. Un esempio è fornito dal fenomeno della formazione dei concetti e lo psicologo che viene in mente a questo proposito è sicuramente Eleanor Rosch, la quale ha studiato i principi di base della categorizzazione. I concetti ci forniscono uno strumento potente per organizzare le conoscenze. Noi siamo in grado di riconoscere facilmente i diversi esemplare di un concetto – per esempio, “gli uccelli” – anche se i singoli esemplari che fanno parte di una categoria sono molto diversi tra loro (l’aquila, la gallina, il pettirosso). L’uso dei concetti, cioè la generalizzazione, è utile perché ci consente di fare previsioni sulle proprietà dei singoli esemplari che appartengono ad una categoria, anche se non abbiamo mai avuto esperienza diretta con essi – per esempio, possiamo fare la predizione che tutti gli uccelli possono volare e mangiare vermi, ma non possono guidare un’automobile o parlare in inglese. Queste previsioni non sono sempre corrette, ma sono utili.
Le statistiche descrittive, in un certo senso, ci fornisco l’analogo dei “prototipi” che, secondo Eleanor Rosch, stanno alla base del processo psicologico di creazione dei concetti. Un prototipo è l’esemplare più rappresentativo di una categoria. In maniera simile, una statistica descrittiva come la media, ad esempio, potrebbe essere intesa come l’osservazione “tipica.”
La statistica descrittiva ci fornisce gli strumenti per riassumere i dati che abbiamo a disposizione in una forma visiva o numerica. Le rappresentazioni grafiche più usate della statistica descrittiva sono gli istogrammi, i diagrammi a dispersione o i box-plot, e gli indici sintetici più comuni sono la media, la mediana, la varianza e la deviazione standard.
12.2 Distribuzioni di frequenze
Per introdurre i principali strumenti della statistica descrittiva considereremo qui i dati raccolti da Zetsche et al. (2019). Questi autori hanno studiato le aspettative negative le quali sono state evidenziate come un meccanismo chiave nel mantenimento e nella reiterazione della depressione. Zetsche et al. (2019) hanno valutato le aspettative di individui depressi circa il loro umore futuro ed si sono chiesti se queste aspettative fossero accurate oppure distorte negativamente.
In uno degli studi descritti viene esaminato un campione costituito da 30 soggetti con almeno un episodio depressivo maggiore e da 37 controlli sani. Gli autori hanno misurato il livello depressivo con il Beck Depression Inventory (BDI-II). Ma qual è la la gravità della depressione riportata dai soggetti nel campione esaminato da Zetsche et al. (2019)?
Dei 67 soggetti considerati, uno non ha completato il BDI-II e quindi abbiamo a disposizione 66 valori del BDI-II. I dati sono riportati nella tabella [tab:bdi2_values]. Per semplicità i dati sono stati ordinati in ordine crescente. È chiaro che i dati grezzi sono di difficile lettura. Poniamoci dunque il problema di creare una rappresentazione sintetica e comprensibile di questo insieme di valori.
Uno dei modi che ci consentono di effettuare una sintesi dei dati è quello di generare una distribuzione di frequenze. Una distribuzione di frequenze è un riepilogo del conteggio della frequenza con cui le modalità osservate in un insieme di dati si verificano in un intervallo di valori.
Per creare una distribuzione di frequenze possiamo procedere effettuando una partizione delle modalità della variabile di interesse in \(m\) classi (denotate con \(\Delta_i\)) tra loro disgiunte. In tale partizione, la classe \(i\)-esima coincide con un intervallo di valori aperto a destra \([a_i, b_i)\) o aperto a sinistra \((a_i, b_i]\). Ad ogni classe \(\Delta_i\) avente \(a_i\) e \(b_i\) come limite inferiore e superiore associamo l’ampiezza \(b_i - a_i\) (non necessariamente uguale per ogni classe) e il valore centrale \(\bar{x}_i\). La scelta delle classi è arbitraria, ma è buona norma non definire classi con un numero troppo piccolo (< 5) di osservazioni. Poiché ogni elemento dell’insieme \(\{x_i\}_{i=1}^n\) appartiene ad una ed una sola classe \(\Delta_i\), possiamo calcolare le quantità elencate di seguito.
La frequenza assoluta \(n_i\) di ciascuna classe, ovvero il numero di osservazioni che ricadono nella classe \(\Delta_i\). Proprietà: \(n_1 + n_2 + \dots + n_m = n\).
La frequenza relativa \(f_i = n_i/n\) di ciascuna classe. Proprietà: \(f_1+f_2+\dots+f_m =1\).
La frequenza cumulata \(N_i\), ovvero il numero totale delle osservazioni che ricadono nelle classi fino alla \(i\)-esima compresa: \(N_i = \sum_{i=1}^m n_i.\)
La frequenza cumulata relativa \(F_i\), ovvero \(F_i = f_1+f_2+\dots+f_m = \frac{N_i}{n} = \frac{1}{n} \sum_{i=1}^m f_i.\)
Calcoliamo ora la distribuzione di frequenza assoluta e la distribuzione di frequenza relativa per i valori del BDI-II del campione clinico di Zetsche et al. (2019). Per costruire una distribuzione di frequenza è innanzitutto necessario scegliere gli intervalli delle classi. Facendo riferimento ai cut-off usati per l’interpretazione del BDI-II, definiamo i seguenti intervalli aperti a destra:
- depressione minima: [0, 13.5),
- depressione lieve: [13.5, 19.5),
- depressione moderata: [19.5, 28.5),
- depressione severa: [28.5, 63).
La distribuzione di frequenza della variabile bdi2 è riportata nella
tabella seguente. Questa distribuzione di frequenza ci aiuta a capire meglio cosa sta succedendo. Se consideriamo la frequenza relativa, ad esempio, possiamo notare che ci sono due valori maggiormente ricorrenti e tali valori corrispondono alle due classi più estreme. Questo ha senso nel caso presente, in quanto il campione esaminato da Zetsche et al. (2019) includeva due gruppi di
soggetti: soggetti sani (con valori BDI-II bassi) e soggetti depressi
(con valori BDI-II alti). In una distribuzione di frequenza tali valori
tipici vanno sotto il nome di mode della distribuzione.
| Limiti delle classi | Freq. ass. | Freq. rel. | Freq. ass. cum. | Freq. rel. cum. |
|---|---|---|---|---|
| \([0, 13.5)\) | 36 | 36/66 | 36 | 36/66 |
| \([13.5, 19.5)\) | 1 | 1/66 | 37 | 37/66 |
| \([19.5, 28.5)\) | 12 | 12/66 | 49 | 49/66 |
| \([28.5, 63)\) | 17 | 17/66 | 66 | 66/66 |
12.2.1 Esercizio con R
Poniamoci ora il problema di costruire la tabella precedente partendo dai dati grezzi messi a disposizione da Zetsche et al. (2019).
Leggiamo i dati assumendo che il file data.mood.csv si trovi nella cartella data contenuta nella working directory.
C’è un solo valore di depressione per ciascun soggetto ma tale valore viene ripetuto tante volte quante volte sono le righe del data.frame associate ad ogni soggetto (ciascuna riga corrispondente ad una prova diversa). È dunque necessario trasformare il data.frame in modo tale da avere un’unica riga per ciascun soggetto, ovvero un unico valore BDI-II per soggetto.
Ci sono dunque 66 soggetti i quali hanno ottenuto i valori sulla scala del BDI-II stampati di seguito (li presento ordinati dal più piccolo al più grande).
sort(bysubj$bdi)
#> [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 2 2 2 2 3
#> [31] 3 3 5 7 9 12 19 22 22 24 25 25 26 26 26 27 27 28 28 30 30 30 31 31 33 33 34 35 35 35
#> [61] 36 39 41 43 43 44Calcolo ora le frequenze assolute per i seguenti intervalli aperti a destra: [0, 13.5), [13.5, 19.5), [19.5, 28.5), [28.5, 63). Esaminando i dati, possiamo notare che 36 soggetti cadono nella prima classe. È però necessario eseguire quest’operazione di conteggio utilizzando R.
Uno dei modi possibili per calcolare le frequenze assolute è quello di usare la funzione cut(). Mediante tal funzione è possibile dividere il campo di variazione (ovvero, la differenza tra il valore massimo di una distribuzione ed il valore minimo) di una variabile continua x in intervalli e codificare ciascun valore x nei termini dell’intervallo a cui appartiene. Tale risultato si ottiene nel modo seguente.
bysubj$bdi_level <- cut(
bysubj$bdi,
breaks = c(0, 13.5, 19.5, 28.5, 63),
include.lowest = TRUE,
labels = c(
"minimal", "mild", "moderate", "severe"
)
)
bysubj$bdi_level
#> [1] moderate severe severe moderate severe severe severe severe moderate severe
#> [11] moderate mild severe minimal minimal minimal severe moderate minimal minimal
#> [21] minimal minimal minimal moderate minimal minimal minimal minimal minimal minimal
#> [31] minimal severe minimal minimal severe minimal moderate minimal minimal minimal
#> [41] severe minimal minimal severe severe moderate severe severe minimal moderate
#> [51] minimal moderate severe moderate moderate minimal minimal minimal minimal minimal
#> [61] minimal minimal minimal minimal minimal minimal
#> Levels: minimal mild moderate severePossiamo ora usare la funzione table() la quale ritorna un elenco che associa la frequenza assoluta a ciascuna modalità della variabile in input – ovvero, la distribuzione di frequenza assoluta.
table(bysubj$bdi_level)
#>
#> minimal mild moderate severe
#> 36 1 12 17Per ottenere la distribuzione di frequenza relativa è sufficiente dividere ciascuna frequenza assoluta per il numero totale di osservazioni:
table(bysubj$bdi_level) / sum(table(bysubj$bdi_level))
#>
#> minimal mild moderate severe
#> 0.54545455 0.01515152 0.18181818 0.25757576In questo modo abbiamo ottenuto le distribuzioni di frequenza assoluta e relativa per i valori del BDI-II dei soggetti di Zetsche et al. (2019):
| Limiti delle classi | Frequenza assoluta | Frequenza relativa |
|---|---|---|
| [0, 13.5) | 36 | 36/66 |
| [13.5, 19.5) | 1 | 1/66 |
| [19.5, 28.5) | 12 | 12/66 |
| [28.5, 63] | 17 | 17/66 |
12.2.2 Osservazione
In una sezione successiva di questo capitolo discuteremo i principi che, secondo Edward Tufte, devono guidare la Data Science. Parlando delle rappresentazioni grafiche dei dati, Edward Tufte ci dice che la prima cosa da fare è “mostrare i dati.” Questa può sembrare una tautologia, considerato che questo è lo scopo della statistica descrittiva: trasformare i dati attraverso vari indici riassuntivi o rappresentazioni grafiche, in modo tale da renderli comprensibili. Tuttavia, spesso le tecniche statistiche vengono usate per nascondere e non per mostrare i dati.
L’uso delle frequenze relative offre un chiaro esempio di questo. Di questi tempi capita spesso di incontrare, sulla stampa, notizie a proposito un nuovo farmaco che, in una prova clinica, ha mostrato risultati incoraggianti che suggeriscono la sua efficacia come possibile trattamento del COVID-19. Alle volte i risultati della sperimentazione clinica sono riportati nei termini di una frequenza relativa. Ad esempio, potremmo leggere che l’uso del farmaco ha portato ad una riduzione del 21% dei ricoveri o dei decessi. Sembra tanto. Ma è necessario guardare i dati! Ovvero, molto spesso, quello che non viene riportato dai comunicati stampa. Infatti, una riduzione del 21% può corrispondere ad un cambiamento dal 5% al 4%. E una riduzione del 44% può corrispondere ad una differenza di 10 contro 18, o di 5 contro 9, o di 15 contro 27. In altri termini, una proporzione, anche grande, può corrispondere ad una differenza assoluta piuttosto piccola: un piccolo passo in avanti, ma non ad un balzo! Per questa ragione, per capire cosa i dati significano, è necessario guardare i dati da diversi punti di vista, utilizzando diverse statistiche descrittive, senza limitarci alla statistica descrittiva che racconta la storia che piace di più. Perché la scelta della statistica descrittiva da utilizzare per riassumere i dati dipende dagli scopi di chi esegue l’analisi statisica: il nostro scopo è quelloi di capire se il farmaco funziona; lo scopo delle compagnie farmaceutiche è quello di vendere il farmaco. Sono obiettivi molto diversi.
12.3 Istogramma
I dati che sono stati sintetizzati in una distribuzione di frequenze possono essere rappresentati graficamente in un istogramma. Un istogramma si costruisce riportando sulle ascisse i limiti delle classi \(\Delta_i\) e sulle ordinate i valori della funzione costante a tratti \[\varphi_n(x)= \frac{f_i}{b_i-a_i}, \quad x\in \Delta_i,\, i=1, \dots, m\] che misura la densità della frequenza relativa della variabile \(X\) nella classe \(\Delta_i\), ovvero il rapporto fra la frequenza relativa \(f_i\) e l’ampiezza (\(b_i - a_i\)) della classe. In questo modo il rettangolo dell’istogramma associato alla classe \(\Delta_i\) avrà un’area proporzionale alla frequenza relativa \(f_i\). Si noti che l’area totale dell’istogramma delle frequenze relative è data della somma delle aree dei singoli rettangoli e quindi vale 1.0.
12.3.1 Esercizio con R
Poniamoci il problema di costruire un istogramma per i dati del BDI-II. Nell’istogramma viene rappresentata la frequenza relativa delle classi: l’area di ogni barra dell’istogramma è proporzionale alla frequenza relativa della classe che la barra rappresenta. Come si trova l’altezza delle barre dell’istogramma? Per la classe [0, 13.5), ad esempio, la frequenza relativa è 36/66. Tale valore corrisponde all’area del rettangolo. Dato che la base del rettangolo è 13.5, l’altezza sarà 36/66 / 13.5, ovvero 0.0404. E così via per le altre barre dell’istogramma.
Una rappresentazione grafica dell’istogramma delle frequenze relative si può ottenere con R utilizzando le funzioni di ggplot2. Il pacchetto ggplot2 è un potente strumento per rappresentare graficamente i dati. Le iniziali del nome, gg, si riferiscono alla ‘’Grammar of Graphics’’, che è un modo di pensare le figure come una serie di layer stratificati. Originariamente descritta da Leland Wilkinson, la grammatica dei grafici è stata aggiornata e applicata in R da Hadley Wickham, il creatore del pacchetto. Per chiarezza, precisiamo che la funzione ggplot() utilizza intervalli aperti a destra.
p1 <- bysubj %>%
ggplot(aes(x = bdi)) +
geom_histogram(
aes(y = ..density..),
breaks = c(0, 13.5, 19.5, 28.5, 44.1) # il valore BDI-II massimo è 44
) +
scale_x_continuous(breaks=c(0, 13.5, 19.5, 28.5, 44.1)) +
labs(
x = "BDI-II",
y = "Densità di frequenza"
) +
theme_apa()
p1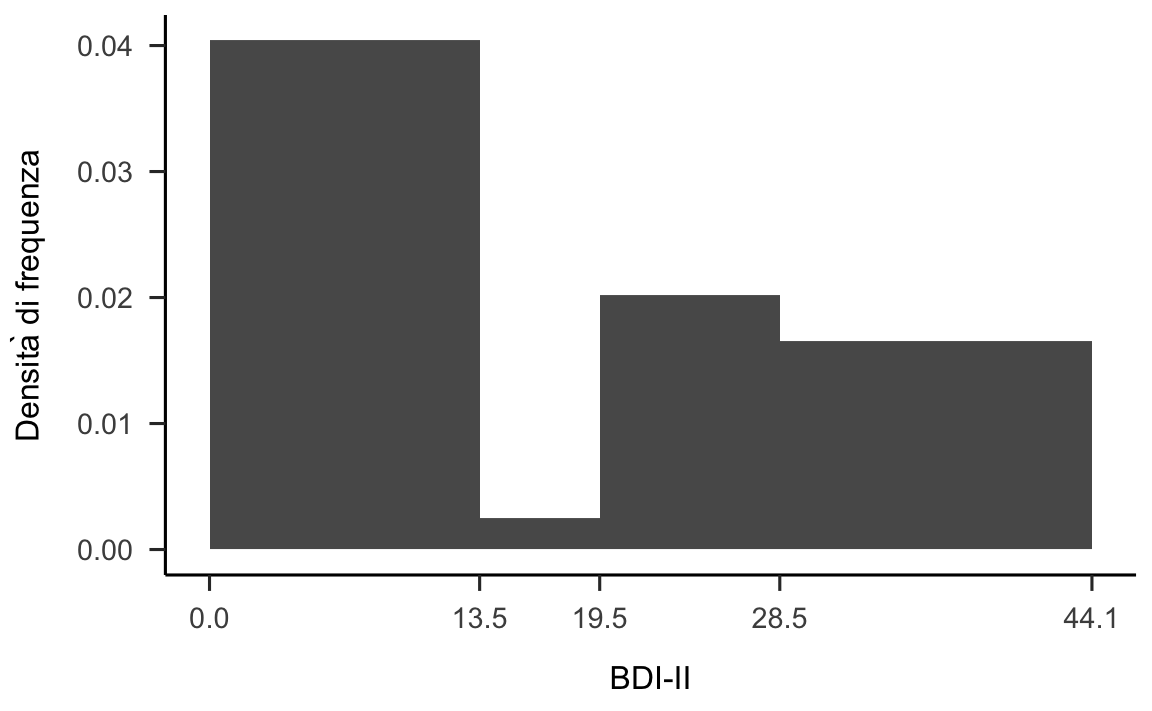
Figura 12.1: Istogramma per i valori BDI-II riportati da Zetsche et al. (2019).
Con i quattro intervalli individuati dai cut-off del BDI-II otteniamo la rappresentazione riportata nella figura 12.1. Nel caso della prima barra dell’istogramma a sinistra, l’ampiezza dell’intervallo è pari a 13.5 e l’area della barra (ovvero, la frequenza relativa) è uguale a 36/66. Dunque l’altezza della barra è uguale a (36 / 66) / 13.5 = 0.040. Lo stesso procedimento si applica per il calcolo dell’altezza degli altri rettangoli.
Anche se nel caso presente è sensato usare ampiezze diverse per gli intervalli delle classi, in generale gli istogrammi si costruiscono utilizzando intervalli riportati sulle ascisse con un’ampiezza uguale. Questo è il caso dell’istogramma seguente il quale è stato generato a partire dagli stessi dati.
p2 <- bysubj %>%
ggplot(aes(x = bdi)) +
geom_histogram(
aes(y = ..density..),
breaks = seq(0, 44.1, length.out = 7)
) +
scale_x_continuous(breaks=c(0.00, 7.35, 14.70, 22.05, 29.40, 36.75, 44.10)) +
labs(
x = "BDI-II",
y = "Densità di frequanza"
) +
theme_apa()
p2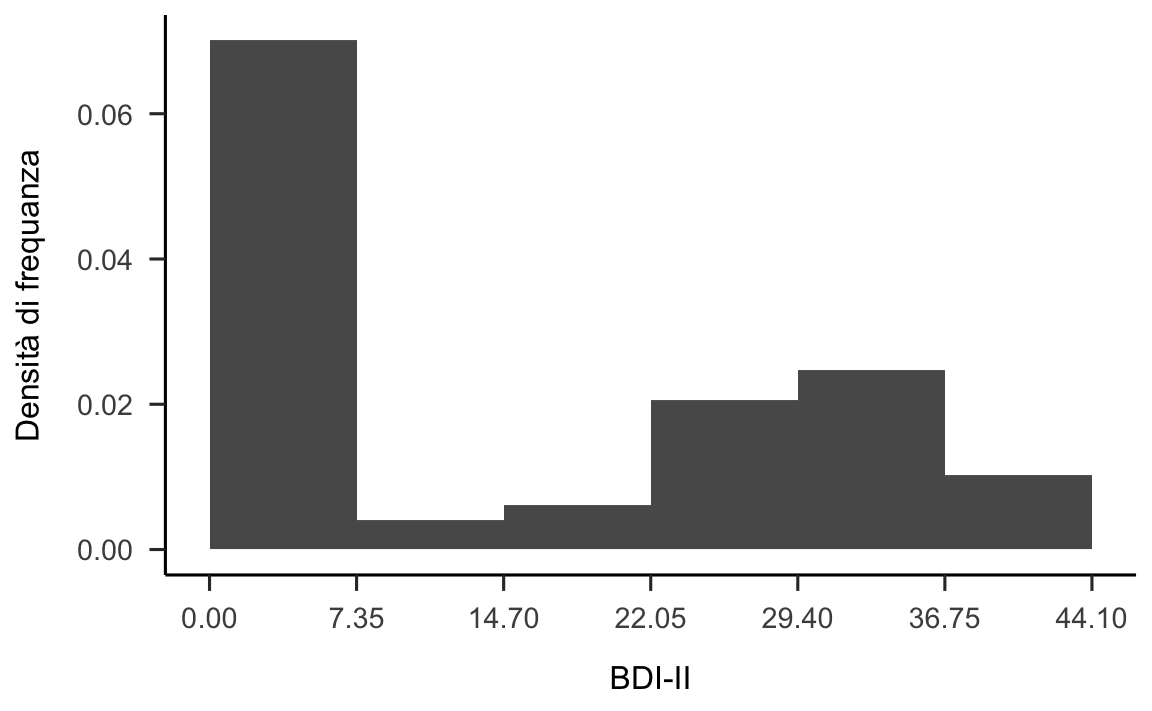
Figura 12.2: Una rappresentazione più comune per l’istogramma dei valori BDI-II di Zetsche et al. (2019) nella quale gli intervalli delle classi hanno ampiezze uguali.
12.4 Funzione di densità empirica
Il confronto tra le figure 12.1 e 12.2 rende chiaro un limite degli istogrammi. È infatti ovvio che il profilo dell’istogramma è arbitrario: a seconda del numero e dei limiti delle classi che vengono scelte, cambiano sia il numero che la forma delle barre dell’istogramma. Questo rende difficile fornire un’interpretazione alle informazioni fornite da un istogramma.
Il problema precedente può essere alleviato utilizzando una rappresentazione alternativa della distribuzione di frequenza, ovvero la stima della densità della frequenza dei dati (detta anche stima kernel di densità). Un modo semplice per pensare a tale rappresentazione, che in inglese va sotto il nome di density plot, è quello di immaginare un grande campione di dati, in modo che diventi possibile definire un enorme numero di classi di equivalenza di ampiezza molto piccola, le quali non risultino vuote. In tali circostanze, la funzione di densità empirica non è altro che il profilo lisciato dell’istogramma. La stessa idea si applica anche quando il campione è più piccolo.
12.4.1 Esercizio con R
Nel caso dei dati del BDI-II otteniamo la reppresentazione fornita dalla figura seguente.
p3 <- bysubj %>%
ggplot(aes(x = bdi)) +
geom_histogram(
aes(y = ..density..),
breaks = seq(0, 44.1, length.out = 7)
) +
geom_density(
aes(x = bdi),
adjust = 0.5,
size = 0.8,
fill = "steelblue3",
alpha = 0.5
) +
labs(
x = "BDI-II",
y = "Densità di frequenza"
) +
theme_apa()
p3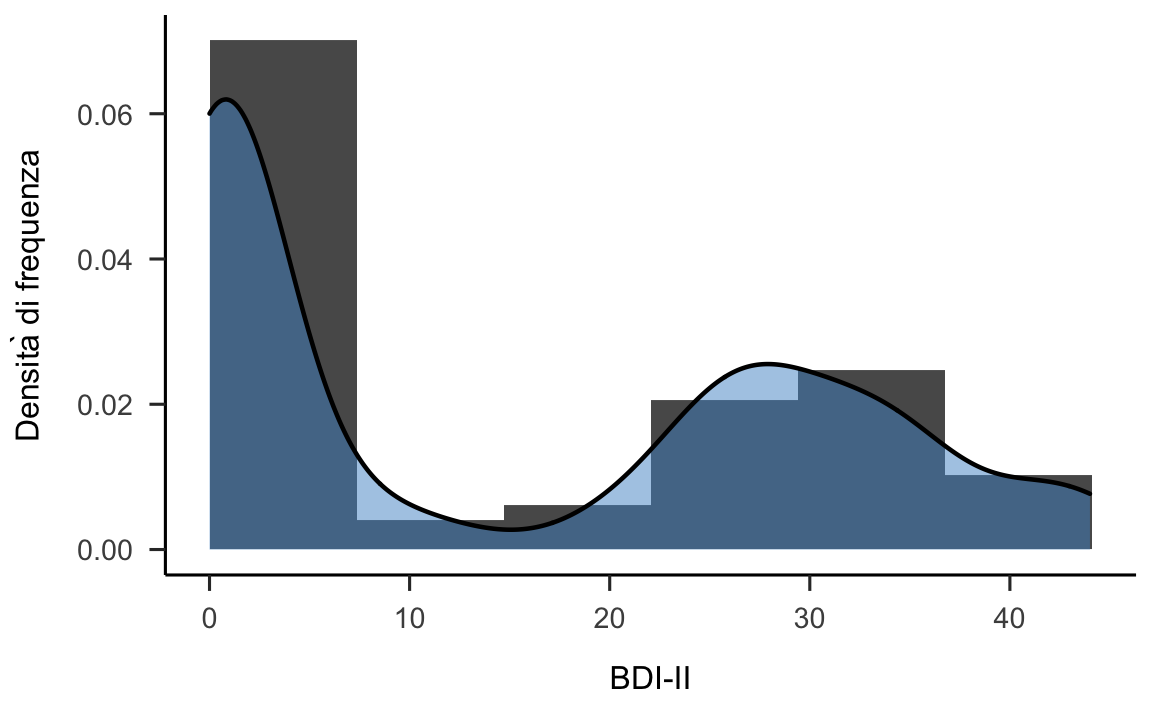
Figura 12.3: Funzione di densità empirica per i valori BDI-II di Zetsche et al. (2019).
Che interpretazione possiamo attribuire alla funzione di densità empirica rappresentata nella figura 12.3? La interpretiamo come abbiamo fatto con gli istogrammi: l’area sottesa al grafico della funzione di densità empirica in un certo intervallo rappresenta la proporzione dei casi della distribuzione che hanno valori compresi nell’intervallo considerato.
12.5 Forma di una distribuzione
In generale, la forma di una distribuzione descrive come i dati si distribuiscono intorno ai valori centrali. Distinguiamo tra distribuzioni simmetriche e asimmetriche, e tra distribuzioni unimodali o multimodali. Un’illustrazione grafica è fornita nella figura seguente.
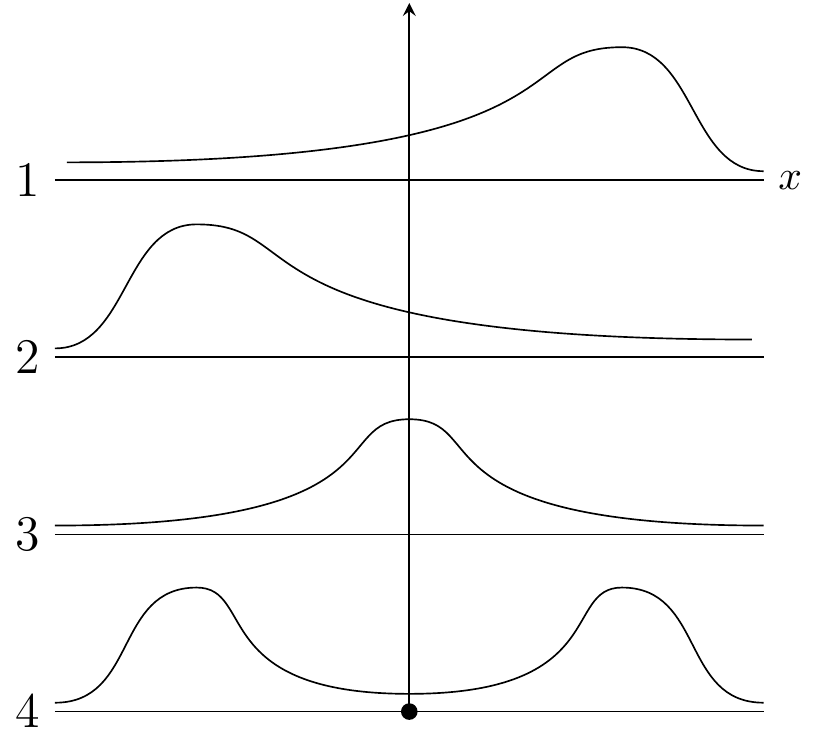
Figura 12.4: 1: Asimmetria negativa. 2: Asimmetria positiva. 3: Distribuzione unimodale. 4: Distribuzione bimodale.
Nel pannello 1 la distribuzione è unimodadle con asimmetria negativa; nel pannello 2 la distribuzione è unimodadle con asimmetria positiva; nel pannello 3 la distribuzione è simmetrica e unimodale; nel pannello 4 la distribuzione è bimodale.
Se consideriamo nuovamente la figura 12.3 possiamo dire che la distribuzione dei valori del BDI-II nel campione considerato da Zetsche et al. (2019) è bimodale.
12.6 Indici di posizione
Nuovamente, se preferite un’introduzione veramente “soft” alla nozione di “tendenza centrale” di una distribuzione statistica, vi rimando nuovamentew al link che ho già suggerito in precedenza.
12.6.1 Quantili
La descrizione della distribuzione dei valori BDI-II di Zetsche et al. (2019) può essere facilitata dalla determinazione di alcuni valori caratteristici che sintetizzano le informazioni contenute nella distribuzione di frequenze. Si dicono quantili (o frattili) quei valori caratteristici che hanno le seguenti proprietà. I quartili sono quei valori che ripartiscono i dati \(x_i\) in quattro parti ugualmente numerose (pari ciascuna al 25% del totale). Il primo quartile, \(q_1\), lascia alla sua sinistra il 25% del campione pensato come una fila ordinata (a destra quindi il 75%). Il secondo quartile \(q_2\) lascia a sinistra il 50% del campione (a destra quindi il 50%). Esso viene anche chiamato mediana. Il terzo quartile lascia a sinistra il 75% del campione (a destra quindi il 25%). Secondo lo stesso criterio, si dicono decili i quantili di ordine \(p\) multiplo di 0.10 e percentili i quantili di ordine \(p\) multiplo di 0.01.
Come si calcolano i quantili? Consideriamo la definizione di quantile non interpolato di ordine \(p\) \((0 < p < 1)\). Si procede innanzitutto ordinando i dati in ordine crescente, \(\{x_1, x_2, \dots, x_n\}\). Ci sono poi due possibilità. Se il valore \(np\) non è intero, sia \(k\) l’intero tale che \(k < np < k + 1\) – ovvero, la parte intera di \(np\). Allora \(q_p = x_{k+1}.\) Se \(np = k\) con \(k\) intero, allora \(q_p = \frac{1}{2}(x_{k} + x_{k+1}).\) Se vogliamo calcolare il primo quartile \(q_1\), ad esempio, utilizziamo \(p = 0.25\). Dovendo calcolare gli altri quantili basta sostituire a \(p\) il valore appropriato[^2].
Gli indici di posizione, tra le altre cose, hanno un ruolo importante, ovvero vengono utilizzati per creare una rappresentazione grafica di una distribuzione di valori che è molto popolare e può essere usata in alternativa ad un istogramma (in realtà vedremo poi come possa essere combinata con un istogramma). Tale rappresentazione va sotto il nome di box-plot.
Per fare un esempio, consideriamo i nove soggetti del campione clinico di Zetsche et al. (2019) che hanno riportato un unico episodio di depressione maggiore. Per tali soggetti i valori ordinati del BDI-II (per semplicità li chiameremo \(x\)) sono i seguenti: 19, 26, 27, 28, 28, 33, 33, 41, 43. Per il calcolo del secondo quartile (non interpolato), ovvero per il calcolo della mediana, dobbiamo considerare la quantità \(np = 9 \cdot 0.5 = 4.5\), non intero. Quindi, \(q_1 = x_{4 + 1} = 27\). Per il calcolo del quantile (non interpolato) di ordine \(p = 2/3\) dobbiamo considerare la quantità \(np = 9 \cdot 2/3 = 6\), intero. Quindi, \(q_{\frac{2}{3}} = \frac{1}{2} (x_{6} + x_{7}) = \frac{1}{2} (33 + 33) = 33\).
12.6.2 Box-plot
Il box-plot (o diagramma a scatola) è uno strumento grafico utile al fine di ottenere informazioni circa la dispersione e l’eventuale simmetria o asimmetria di una distribuzione. Per costruire un box-plot si rappresenta sul piano cartesiano un rettangolo (cioè la “scatola”) di altezza arbitraria la cui base corrisponde alla dist intanza interquartile (IQR = \(q_{0.75} - q_{0.25}\)). La linea interna alla scatola rappresenta la mediana \(q_{0.5}\). Si tracciano poi ai lati della scatola due segmenti di retta i cui estremi sono detti “valore adiacente” inferiore e superiore. Il valore adiacente inferiore è il valore più piccolo tra le osservazioni che risulta maggiore o uguale al primo quartile meno la distanza corrispondente a 1.5 volte la distanza interquartile. Il valore adiacente superiore è il valore più grande tra le osservazioni che risulta minore o uguale a \(Q_3+1.5\) IQR. I valori esterni ai valori adiacenti (chiamati valori anomali) vengono rappresentati individualmente nel box-plot per meglio evidenziarne la presenza e la posizione.
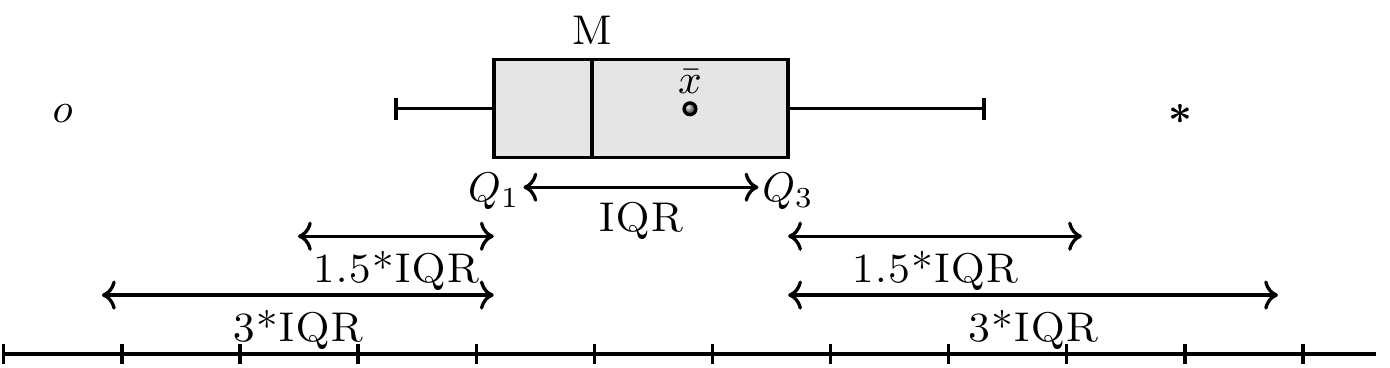
Figura 12.5: Box-plot: \(M\) è la mediana, \(\bar{x}\) è la media aritmetica e IQR è la distanza interquartile (\(Q_3 - Q_1\)).
Consideriamo ora un caso concreto nel quale viene utilizzato un box-plot. Nel caso dei dati di Zetsche et al. (2019) ci chiediamo in che modo si differenziano le distribuzioni del BDI-II tra i due gruppi considerati, ovvero tra il gruppo dei pazienti e il gruppo di controllo.
bysubj <- df %>%
group_by(esm_id, group) %>%
summarise(
bdi = mean(bdi),
nr_of_episodes = mean(nr_of_episodes, na.rm = TRUE)
) %>%
na.omit()
#> `summarise()` has grouped output by 'esm_id'. You can override using the `.groups` argument.
bysubj %>%
ggplot(aes(x=group, y=bdi)) +
geom_boxplot() +
labs(
x = "Gruppo",
y = "BDI-II"
) +
theme_apa()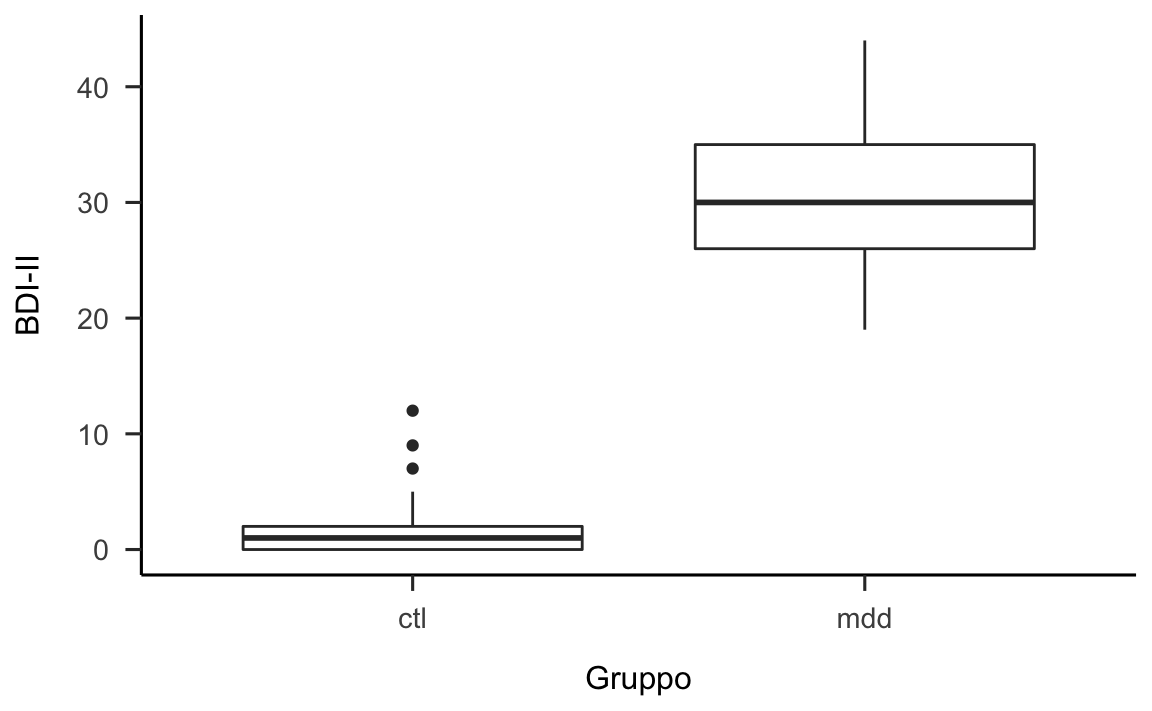
La figura 12.6 fornisce due rappresentazioni grafiche che possono essere utilizzate per rispondere a questa domanda.
library("patchwork")
bysubj <- df %>%
group_by(esm_id, group) %>%
summarise(
bdi = mean(bdi),
nr_of_episodes = mean(nr_of_episodes, na.rm = TRUE)
) %>%
na.omit()
#> `summarise()` has grouped output by 'esm_id'. You can override using the `.groups` argument.
p1 <- bysubj %>%
ggplot(aes(x=group, y=bdi)) +
geom_violin(trim=FALSE) +
geom_dotplot(binaxis='y', stackdir='center', dotsize=0.7) +
labs(
x = "Gruppo",
y = "BDI-II"
#, caption = "Fonte: Zetsche, Buerkner, & Renneberg (2020)"
)
p2 <- bysubj %>%
ggplot(aes(x=group, y=bdi)) +
geom_violin(trim=FALSE) +
geom_boxplot(width=0.05) +
labs(
x = "Gruppo",
y = "BDI-II"
#, caption = "Fonte: Zetsche, Buerkner, & Renneberg (2020)"
)
p1 + p2
#> `stat_bindot()` using `bins = 30`. Pick better value with `binwidth`.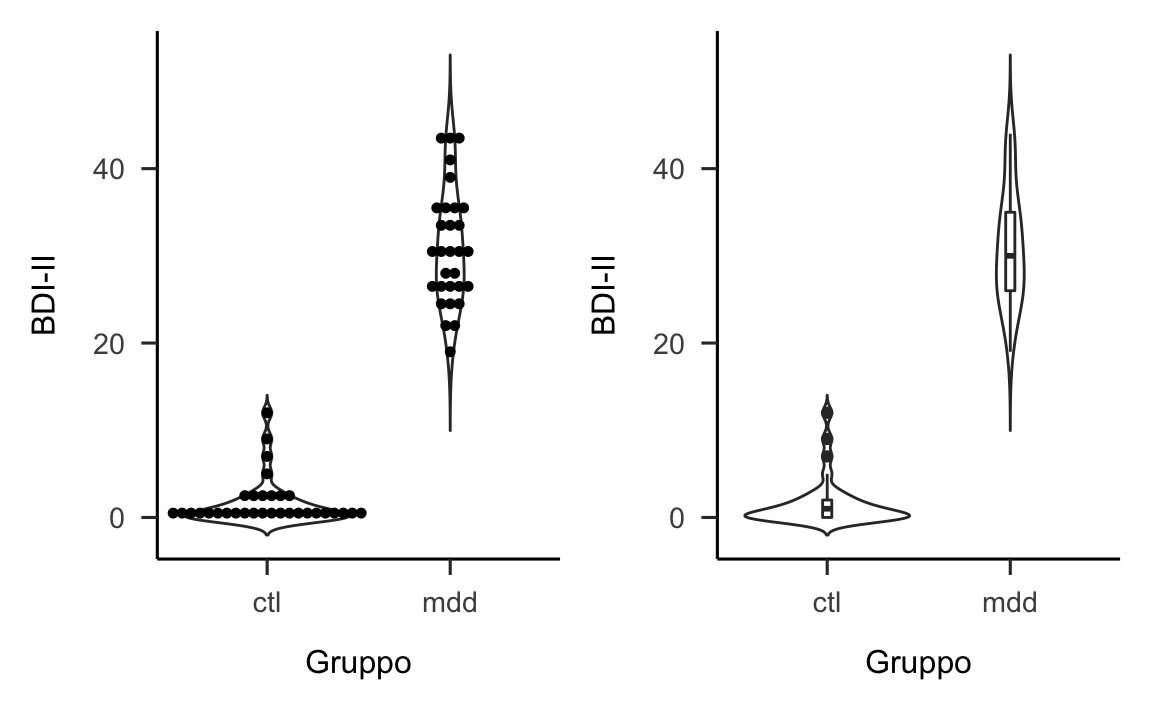
Figura 12.6: Due versioni di un violin plot per i valori BDI-II di ciascuno dei due gruppi di soggetti esaminati da Zetsche et al. (2019).
Nella figura 12.6 sinistra sono rappresentati i dati grezzi: questa è la pratica migliore quando il numero di osservazioni è piccolo. La linea curva che circonda (simmetricamente) le osservazioni è l’istogramma lisciato che abbiamo descritto in precedenza. Nella figura 12.6 destra sono rappresentanti gli stessi dati: la funzione di densità empirica è la stessa di prima, ma al suo interno viene collocato un box-plot. Questa seconda rappresentazione è da preferirsi quando ci sono molte osservazioni e non è utile rappresentare singolarmente ciascun dato. Entrambe le rappresentazioni suggeriscono che la distribuzione dei dati è all’incirca simmetrica nel gruppo clinico (codificato come mdd). Il gruppo di controllo (ctl) mostra invece un’asimmetria positiva, con tre osservazioni evidenziate nel boxplot come dei “valori anomali,” dato che si discostano dalla mediana di una quantità maggiore di 1.5 IQR.
12.6.3 L’eccellenza grafica
Non c’è un modo “corretto” per rappresentare in forma grafica un insieme di dati. Ciascuno dei grafici che abbiamo discusso ha i suoi pregi e i suoi difetti. Un ricercatore che ha influenzato molto il modo in cui viene realizzata la visualizzazione dei dati scientifici è Edward Tufte, soprannominato dal New York Times il “Leonardo da Vinci dei dati.” Secondo Tufte, “l’eccellenza nella grafica consiste nel comunicare idee complesse in modo chiaro, preciso ed efficiente.” Nella visualizzazione delle informazioni, l’“eccellenza grafica” ha l’obiettivo di comunicare al lettore il maggior numero di idee nel minor tempo possibile, con meno inchiostro possibile, usando il minor spazio possibile. Secondo Tufte (2001), le rappresentazioni grafiche dovrebbero:
- mostrare i dati;
- indurre l’osservatore a riflettere sulla sostanza piuttosto che sulla progettazione grafica, o qualcos’altro;
- evitare di distorcere quanto i dati stanno comunicando (“integrità grafica”);
- presentare molte informazioni in forma succinta;
- rivelare la coerenza tra le molte dimensioni dei dati;
- incoraggiare l’osservatore a comparare differenti porzioni di dati;
- rivelare i dati a diversi livelli di dettaglio, da una visione ampia alla struttura di base;
- servire ad uno scopo preciso (descrizione, esplorazione, o la risposta a qualche domanda);
- essere fortemente integrate con le descrizioni statistiche e verbali dei dati fornite nel testo.
In base a questi principi, la funzione di densità empirica fornisce una rappresentazione migliore dei dati di Zetsche et al. (2019) di quanto lo faccia un istogramma. Inoltre, se oltre al grupppo di appartenenza non ci sono altre dimensioni importanti da mettere in evidenza, allora la nostra scelta dovrebbe ricadere sul pannello di sinistra della figura 12.6. Il seguente link fornisce diverse interessanti illustrazioni dei principi elencati sopra.
12.7 Indici di tendenza centrale
L’analisi grafica, esaminata in precedenza, costituisce la base di partenza di qualsivoglia analisi quantitativa dei dati. Tramite l’analisi grafica possiamo capire alcune caratteristiche importanti di una distribuzione: per esempio, se è simmetrica o asimmetrica; oppure se è unimodale o multimodale. Successivamente, possiamo calcolare degli indici numerici che descrivono in modo sintetico le caratteristiche di base dei dati esaminati. Tra le misure di tendenza centrale, ovvero tra gli indici che forniscono un’idea dei valori attorno ai quali sono prevalentemente concentrati i dati di un campione, quella più comunemente usata è la media.
12.7.1 Media
Tutti conosciamo la media aritmetica di \(\{x_1, x_2, \dots, x_n\}\), ovvero il numero reale \(\bar{x}\) definito da \[\begin{equation} \bar{x}=\frac{1}{n}\sum_{i=1}^n x_i. \tag{12.1} \end{equation}\] Nell’eq. (12.1) abbiamo usato la notazione delle sommatorie per descrivere una somma di valori. Questa notazione è molto usata in statistica e viene descritta in Appendice.
La media gode della seguente importante proprietà: la somma degli scarti tra ciascuna modalità \(x_i\) e la media aritmetica \(\bar{x}\) è nulla, cioè \[ \sum_{i=1}^n (x_i - \bar{x}) = 0.\notag \label{eq:diffmeansumzero}\] Infatti, \[\begin{aligned} \sum_{i=1}^n (x_i - \bar{x}) &= \sum_i x_i - \sum_i \bar{x}\notag\\ &= \sum_i x_i - n \bar{x}\notag\\ &= \sum_i x_i - \sum_i x_i = 0.\notag\end{aligned} \]
Ciò ci consente di pensare alla media come al baricentro della distribuzione.
Un’altra proprietà della media è la seguente. La somma dei quadrati degli scarti tra ciascuna modalità \(x_i\) e una costante arbitraria \(a \in \Re\), cioè \[\varphi(a) = \sum_{i=1}^n (x_i - a)^2,\notag\] è minima per \(a = \bar{x}\).
Il concetto statistico di media ha suscitato molte battute. Per esempio, il fatto che, in media, ciascuno di noi ha un numero di gambe circa pari a 1.9999999. Oppure, il fatto che, in media, ciascuno di noi ha un testicolo. Ma la media ha altri problemi, oltre al fatto di ispirare battute simili alle precedenti. In particolare, dobbiamo notare che la media non è sempre l’indice che meglio rappresenta la tendenza centrale di una distribuzione. In particolare, ciò non accade quando la distribuzione è asimmetrica, o in presenza di valori anomali (outlier) – si veda il pannello di destra della figura 12.6. In tali circostanze, la tendenza centrale della distribuzione è meglio rappresentata dalla mediana o dalla media spuntata.
12.7.1.1 Esercizio con R
Calcoliamo la media dei valori BDI-II per i due gruppi di soggetti di Zetsche et al. (2019).
12.7.2 Media spuntata
La media spuntata \(\bar{x}_t\) (trimmed mean) non è altro che la media dei dati calcolata considerando solo il 90% (o altra percentuale) dei dati centrali. Per calcolare \(\bar{x}_t\) si ordinando i dati secondo una sequenza crescente, \(x_1 \leq x_2 \leq x_3 \leq \dots \leq x_n\), per poi eliminare il primo 5% e l’ultimo 5% dei dati della serie così ordinata. La media spuntata è data dalla media aritmetica dei dati rimanenti.
12.7.2.1 Esercizio con R
Calcoliamo la media spuntata dei valori BDI-II per i due gruppi di soggetti di Zetsche et al. (2019) escludendo il 10% dei valori più estremi in ciascun gruppo.
12.7.3 Moda e mediana
In precedenza abbiamo già incontrato altri due popolari indici di tendenza centrale: la moda (Mo), ovvero il valore centrale della classe con la frequenza massima (può succedere che una distribuzione abbia più mode; in tal caso si dice multimodale e questo operatore perde il suo significato di indice di tendenza centrale) e la mediana \(\tilde{x}\).
12.7.3.1 Esercizio con R
Calcoliamo i quantili di ordine 0.25, 0.5 e 0.75 dei valori BDI-II per i due gruppi di soggetti di Zetsche et al. (2019).
bysubj %>%
group_by(group) %>%
summarise(
q25 = quantile(bdi, probs = 0.25),
q50 = quantile(bdi, probs = 0.50),
q75 = quantile(bdi, probs = 0.75)
)
#> # A tibble: 2 x 4
#> group q25 q50 q75
#> <fct> <dbl> <dbl> <dbl>
#> 1 ctl 0 1 2
#> 2 mdd 26 30 3512.8 Indici di dispersione
Le medie e gli indici di posizione descritti in precedenza forniscono delle sintesi dei dati che mettono in evidenza la tendenza centrale delle osservazioni. Tali indici, tuttavia, non considerano un aspetto importante della distribuzione dei dati, ovvero la variabilità dei valori numerici della variabile statistica. È dunque necessario sintetizzare la distribuzione di una variabile statistica oltre che con le misure di posizione anche tramite l’utilizzo di indicatori che valutino la dispersione delle unità statistice.
Anche in questo caso, un’introduzione “soft” è fornita nel link.
12.8.1 Indici basati sull’ordinamento dei dati
È possibile calcolare degli indici di variabilità basati sull’ordinamento dei dati. L’indice più ovvio è l’intervallo di variazione, ovvero la distanza tra il valore massimo e il valore minimo di una distribuzione di modalità, mentre in precedenza abbiamo già incontrato la differenza interquartile. Questi due indici, però, hanno il limite di essere calcolati sulla base di due soli valori della distribuzione (\(x_{\text{max}}\) e \(x_{\text{mini}}\), oppure \(x_{0.25}\) e \(x_{0.75}\)). Pertanto non utilizzano tutte le informazioni che sono disponibili. Inoltre, l’intervallo di variazione ha il limite di essere pesantemente influenzato dalla presenza di valori anomali.
12.8.2 Varianza
Dati i limiti delle statistiche precedenti è più comune misurare la variabilità di una variabile statistica come la dispersione dei dati attorno ad un indice di tendenza centrale. Infatt, la misura di variabilità di gran lunga più usata per valutare la variabilità di una variabile statistica è senza dubbio la varianza. La varianza \[\begin{equation} s^2 = \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^2 \tag{12.2} \end{equation}\] è la media dei quadrati degli scarti \(x_i - \bar{x}\) tra ogni valore e la media della distribuzione. La varianza è una misura di dispersione più complessa di quelle esaminate in precedenza. È appropriata solo nel caso di distribuzioni simmetriche e, anch’essa, è fortemente influenzata dai valori anomali. Inoltre, è espressa in un’unità di misura che è il quadrato dell’unità di misura dei dati originari e quindi ad essa non può essere assegnata un’interpretazione intuitiva.
12.8.2.1 Esercizio con R
Calcoliamo la varianza dei punteggi BDI-II nei due gruppi di soggetti di Zetsche et al. (2019).
12.8.3 Deviazione standard
Per le ragioni espresse sopra, la misura più usata della dispersione di una distribuzione di dati è la deviazione standard, ovvero la radice quadrata della varianza. A differenza della varianza, dunque, la deviazione standard è espressa nella stessa unità di misura dei dati. Come nel caso della varianza, anche la deviazione standard \(s\) dovrebbe essere usata soltanto quando la media è adeguata per misurare il centro della distribuzione, ovvero, nel caso di distribuzioni simmetriche. Come nel caso della media \(\bar{x}\), anche la deviazione standard è fortemente influenzata dai dati anomali (outlier), ovvero dalla presenza di uno o di pochi dati che sono molto più distanti dalla media rispetto agli altri valori della distribuzione. Quando tutte le osservazioni sono uguali, \(s=0\), altrimenti \(s > 0\).
Alla deviazione standard può essere assegnata una semplice interpretazione: la deviazione standard è simile (ma non identica) allo scostamento medio semplice dalla media. La deviazione standard ci dice, dunque, quanto sono distanti, in media, le singole osservazioni dal centro della distribuzione.
12.8.3.1 Esercizio con R
Calcoliamo la deviazione standard per il BDI-II dei due gruppi di soggetti di Zetsche et al. (2019).
12.8.4 Deviazione mediana assoluta
Una misura robusta della dispersione statistica di un campione è la deviazione mediana assoluta (Median Absolute Deviation, MAD) definita come la mediana del valore assoluto delle deviazioni dei dati dalla mediana, ovvero:
\[ {\displaystyle \operatorname {MAD} =\operatorname {median} \left(\ \left|X_{i}-\operatorname {median} (X)\right|\ \right)} \] Nel caso di una distribuzione dei dati unimodale simmetrica di forma campanulare (ovvero, normale), si ha che
\[ {\displaystyle \text{deviazione standard} \approx 1.4826\ \operatorname {MAD} .\,} \]
Pertanto, solitamente i software restituiscono il valore MAD moltiplicato per una tale costante.
12.8.4.1 Esercizio con R
Calcoliamo il valore MAD per il BDI-II dei due gruppi di soggetti di Zetsche et al. (2019).
Oppure, per i due gruppi:
12.8.5 Indici di variabilità relativi
A volte può essere interessante effettuare un confronto fra due misure di variabilità di grandezze incommensurabili, ovvero di caratteri rilevati mediante differenti unità di misura. In questi casi, le misure di variabilità precedentemente descritte si rivelano inadeguate in quanto dipendono dall’unità di misura adottata. Diventa dunque necessario ricorrere a particolari numeri adimensionali detti indici relativi di variabilità. Il più importante di tali indici è il coefficiente di variazione, ovvero il numero puro \[C_v = \frac{\sigma}{\bar{x}}\] ottenuto dal rapporto tra la deviazione standard e la media dei dati. Un altro indice relativo di variabilità è la differenza interquartile rapportata al primo quartile oppure al terzo quartile oppure alla mediana, cioè: \[\frac{x_{0.75} - x_{0.25}}{x_{0.25}}, \qquad \frac{x_{0.75} - x_{0.25}}{x_{0.75}}, \qquad \frac{x_{0.75} - x_{0.25}}{x_{0.50}}.\notag\]
12.9 Le relazioni tra variabili
Zetsche et al. (2019) hanno misurato il livello di depressione dei soggetti del loro esperimento utilizzando due scale psicometriche: il Beck Depression Inventory II (BDI-II) e la Center for Epidemiologic Studies Depression Scale (CES-D). Il BDI-II è uno strumento self-report che valutare la presenza e l’intensità di sintomi depressivi in pazienti adulti e adolescenti di almeno 13 anni di età con diagnosi psichiatrica mentre la CES-D è una scala self-report progettata per misurare i sintomi depressivi che sono stati vissuti nella settimana precedente nella popolazione generale, specialmente quella degli adolescenti/giovani adulti. Una domanda ovvia che ci può venire in mente è: quanto sono simili le misure ottenute mediante queste due scale?
È chiaro che i numeri prodotti dalle scale BDI-II e CES-D non possono essere identici, e questo per due motivi: (1) la presenza degli errori di misurazione e (2) l’unità di misura delle due variabili. L’errore di misurazione corrompe sempre, almeno in parte, qualunque operazione di misurazione. E questo è vero specialmente in psicologia dove l’attendibilità degli strumenti di misurazione è minore che in altre discipline (quali la fisica, ad esempio). Il secondo motivo per cui i valori delle scale BDI-II e CES-D non possono essere uguali è che l’unità di misura delle due scale è arbitraria. Infatti, qual è l’unità di misura della depressione? Chi può dirlo! Ma, al di là delle differenze derivanti dall’errore di misurazione e dalla differente unità di misura, ci aspettiamo che, se le due scale misurano entrambe lo stesso costrutto, allora i valori prodotti dalle due scale dovranno essere tra loro linearmente associati. Per capire cosa si intende con “associazione lineare” iniziamo a guardare i dati. Per fare questo utilizziamo una rappresentazione grafica che va sotto il nome di diagramma a dispersione.
12.9.1 Diagramma a dispersione
Il diagramma di dispersione è la rappresentazione grafica delle coppie di punti individuati dalle variabili BDI-II e CES-D, e si ottiene ponendo, ad esempio, i valori BDI-II sull’asse delle ascisse e quelli del CES-D sull’asse delle ordinate. In tale grafico, fornito dalla figura 12.7, cascun punto corrisponde ad un individuo del quale, nel caso presente, conosciamo il livello di depressione misurato dalle due scale psicometriche.
bysubj <- df %>%
group_by(esm_id, group) %>%
summarise(
bdi = mean(bdi),
cesd = mean(cesd_sum)
) %>%
na.omit() %>%
ungroup()
#> `summarise()` has grouped output by 'esm_id'. You can override using the `.groups` argument.
m_cesd <- mean(bysubj$cesd)
m_bdi <- mean(bysubj$bdi)
FONT_SIZE <- 10
p <- bysubj %>%
ggplot(
aes(x=bdi, y=cesd, color=group)) +
geom_point(size=1) +
geom_hline(yintercept= m_cesd, linetype="dashed", color = "gray") +
geom_vline(xintercept = m_bdi, linetype="dashed", color = "gray") +
geom_text(x=-1, y=16, label="I", color = "gray", size=FONT_SIZE) +
geom_text(x=0, y=46, label="IV", color = "gray", size=FONT_SIZE) +
geom_text(x=18, y=46, label="III", color = "gray", size=FONT_SIZE) +
geom_text(x=18, y=16, label="II", color = "gray", size=FONT_SIZE) +
labs(
x = "BDI-II",
y = "CESD"
) +
theme_apa() +
theme(legend.position="none")
p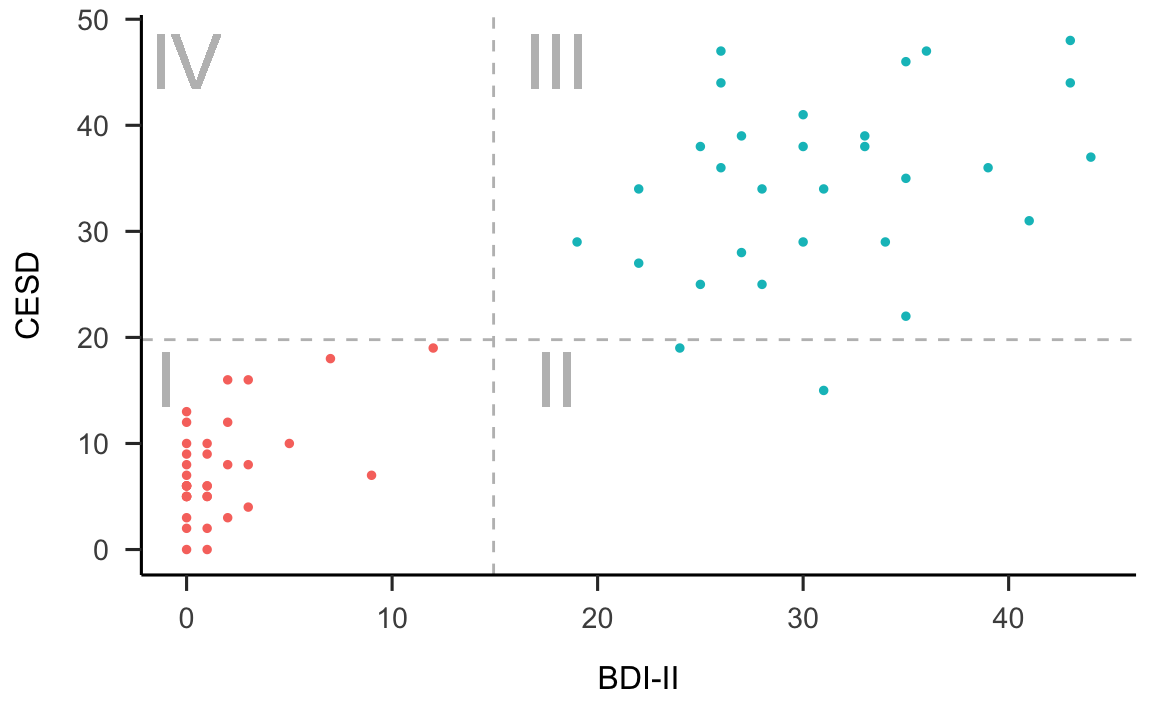
Figura 12.7: Associazione tra le variabili BDI-II e CES-D nello studio di Zetsche et al. (2019). In rosso sono rappresentate le osservazioni del gruppo di controllo; in blu quelle dei pazienti.
Dalla figura 12.7 possiamo vedere che i dati mostrano una certa tendenza a disporsi attorno ad una retta – nel gergo statistico, questo fatto viene espresso dicendo che i punteggi CES-D tendono ad essere linearmente associati ai punteggi BDI-II. È ovvio, tuttavia, che tale relazione lineare è lungi dall’essere perfetta – se fosse perfetta, tutti i punti del diagramma a dispersione si disporrebbero esattamente lungo una retta.
Il problema che ci poniamo è quello di trovare un indice numerico che descriva di quanto la nube di punti si discosta da una perfetta relazione lineare tra le due variabili. Per risolvere tale problema dobbiamo specificare un indice statistico che descriva la direzione e la forza della relazione lineare tra le due variabili. Ci sono vari indici statistici che possiamo utilizzare a questo scopo.
12.9.2 Covarianza
Iniziamo a considerare il più importante di tali indici, chiamato covarianza. In realtà la definizione di questo indice non ci sorprenderà più di tanto in quanto, in una forma solo apparentemente diversa, l’abbiamo già incontrato in precedenza. Ci ricordiamo infatti che la varianza di una generica variabile \(X\) è definita come la media degli scarti quadratici di ciascuna osservazione dalla media: \[\begin{equation} S_{XX} = \frac{1}{n} \sum_{i=1}^n(X_i - \bar{X}) (X_i - \bar{X}). \tag{12.3} \end{equation}\] Infatti, la varianza viene talvolta descritta come la “covarianza di una variabile con sé stessa.”
Adesso facciamo un passo ulteriore. Invece di valutare la dispersione di una sola variabile, chiediamoci come due variabili \(X\) e \(Y\) “variano insieme” (co-variano). È facile capire come una risposta a tale domanda possa essere fornita da una semplice trasformazione della formula precedente che diventa: \[\begin{equation} S_{XY} = \frac{1}{n} \sum_{i=1}^n(X_i - \bar{X}) (Y_i - \bar{Y}). \tag{12.4} \end{equation}\] L’eq. (12.4) ci fornisce dunque la definizione della covarianza.
Per capire il significato dell’eq. (12.4), supponiamo di dividere il grafico della figura 12.7 in quattro quadranti definiti da una retta verticale passante per la media dei valori BDI-II e da una retta orizzontale passante per la media dei valori CES-D. Numeriamo i quadranti partendo da quello in basso a sinistra e muovendoci in senso antiorario.
Se prevalgono punti nel I e III quadrante, allora la nuvola di punti avrà un andamento crescente (per cui a valori bassi di \(X\) tendono ad associarsi valori bassi di \(Y\) e a valori elevati di \(X\) tendono ad associarsi valori elevati di \(Y\)) e la covarianza segno positivo. Mentre se prevalgono punti nel II e IV quadrante la nuvola di punti avrà un andamento decrescente (per cui a valori bassi di \(X\) tendono ad associarsi valori elevati di \(Y\) e a valori elevati di \(X\) tendono ad associarsi valori bassi di \(Y\)) e la covarianza segno negativo. Dunque, il segno della covarianza ci informa sulla direzione della relazione lineare tra due variabili: l’associazione lineare si dice positiva se la covarianza è positiva, negativa se la covarianza è negativa.
Il segno della covarianza ci informa sulla direzione della relazione, ma invece il valore assoluto della covarianza ci dice ben poco. Esso, infatti, dipende dall’unità di misura delle variabili. Nel caso presente questo concetto è difficile da comprendere, dato che le due variabili in esame non hanno un’unità di misura (ovvero, hanno un’unità di misura arbitraria e priva di significato). Ma quest’idea diventa chiara se pensiamo alla relazione lineare tra l’altezza e il peso delle persone, ad esempio. La covarianza tra queste due quantità è certamente positiva, ma il valore assoluto della covarianza diventa più grande se l’altezza viene misurata in millimetri e il peso in grammi, e diventa più piccolo l’altezza viene misurata in metri e il peso in chilogrammi. Dunque, il valore della covarianza cambia al mutare dell’unità di misura delle variabili anche se l’associazione tra le variabili resta costante.
12.9.3 Correlazione
Dato che il valore assoluto della covarianza è di difficile interpretazione – in pratica, non viene mai interpretato – è necessario trasformare la covarianza in modo tale da renderla immune alle trasformazioni dell’unità di misura delle variabili. Questa operazione si dice standardizzazione e corrisponde alla divisione della covarianza per le deviazioni standard (\(s_X\), \(s_Y\)) delle due variabili:
\[\begin{equation} r_{XY} = \frac{S_{XY}}{s_X s_Y}. \tag{12.5} \end{equation}\] La quantià che si ottiene in questo modo viene chiamata correlazione di Bravais-Pearson (dal nome degli autori che, indipendentemente l’uno dall’altro, la hanno introdotta).
Il coefficiente di correlazione ha le seguenti proprietà:
- ha lo stesso segno della covarianza, dato che si ottiene dividendo la covarianza per due numeri positivi;
- è un numero puro, cioè non dipende dall’unità di misura delle variabili;
- assume valori compresi tra -1 e +1.
Ad esso possiamo assegnare la seguente interpretazione:
- \(r_{XY} = -1\) \(\rightarrow\) perfetta relazione negativa: tutti i punti si trovano esattamente su una retta con pendenza negativa (dal quadrante in alto a sinistra al quadrante in basso a destra);
- \(r_{XY} = +1\) \(\rightarrow\) perfetta relazione positiva: tutti i punti si trovano esattamente su una retta con pendenza positiva (dal quadrante in basso a sinistra al quadrante in alto a destra);
- \(-1 < r_{XY} < +1\) \(\rightarrow\) presenza di una relazione lineare di intensità diversa;
- \(r_{XY} = 0\) \(\rightarrow\) assenza di relazione lineare tra \(X\) e \(Y\).
Per i dati della figura 12.7, la covarianza è 207.426. Il segno positivo della covarianza ci dice che tra le due variabili c’è un’associazione lineare positiva. Per capire qual è l’intensità della relazione lineare tra le due variabili calcoliamo la correlazione. Essendo le deviazioni standard del BDI-II e del CES-D rispettavamente uguali a 15.37 e 14.93, la correlazione diventa uguale a \(\frac{207.426}{15.38 \cdot 14.93} = 0.904.\) Tale valore è prossimo a 1.0, il che vuol dire che i punti del diagramma a dispersione non si discostano troppo da una retta con una pendenza positiva.
12.10 Correlazione e causazione
Facendo riferimento nuovamente alla figura 12.7, possiamo dire che, in molte applicazioni (ma non nel caso presente!) l’asse \(x\) rappresenta una quantità nota come variabile indipendente e l’interesse si concentra sulla sua influenza sulla variabile dipendente tracciata sull’asse \(y\). Ciò presuppone però che sia nota la direzione in cui l’influenza causale potrebbe risiedere. È importante tenere bene a mente che la correlazione è soltanto un indice descrittivo della relazione lineare tra due variabili e in nessun caso può essere usata per inferire alcunché sulle relazioni causali che legano le variabili. È ben nota l’espressione: “correlazione non significa causazione.”
Di opinione diversa era invece Karl Pearson (1911), il quale ha affermato:
Quanto spesso, quando è stato osservato un nuovo fenomeno, sentiamo che viene posta la domanda: ‘qual è la sua causa?’ Questa è una domanda a cui potrebbe essere assolutamente impossibile rispondere. Invece, può essere più facile rispondere alla domanda: ‘in che misura altri fenomeni sono associati con esso?’ Dalla risposta a questa seconda domanda possono risultare molte preziose conoscenze.
Che alla seconda domanda posta da Pearson sia facile rispondere è indubbio. Che la nostra comprensione di un fenomeno possa aumentare sulla base delle informazioni fornite unicamente dalle correlazioni, invece, è molto dubbio e quasi certamente falso.
12.10.1 Usi della correlazione
Anche se non può essere usata per studiare le relazioni causali, la correlazione viene usata per molti altri scopi tra i quali, per esempio, quello di misurare la validità concorrente di un test psiologico. Se un test psicologico misura effettivamente ciò che ci si aspetta che misuri (nel caso dell’esempio presente, la depressione), allora dovremo aspettarci che fornisca una correlazione alta con risultati di altri test che misurano lo stesso costrutto – come nel caso dei dati di (Zetsche et al., 2019). Un’altra proprietà desiderabile di un test psicometrico è la validità divergente: i risultati di test psicometrici che misurano costrutti diversi dovrebbero essere poco associati tra loro. In altre parole, in questo secondo caso dovremmo aspettarci che la correlazione sia bassa.
12.10.2 Correlazione di Spearman
Una misura alternativa della relazione lineare tra due variabili è fornita dal coefficiente di correlazione di Spearman e dipende soltanto dalla relazione d’ordine dei dati, non dagli specifici valori dei dati. Tale misura di associazione è appropriata quando, del fenomeno in esame, gli psicologi sono stati in grado di misurare soltanto le relazioni d’ordine tra le diverse modalità della risposta dei soggetti, non l’intensità della risposta. Le variabili psicologiche che hanno questa proprietà si dicono ordinali. Nel caso di variabili ordinali, non è possibile sintetizzare i dati mediante le statistiche descrittive che abbiamo introdotto in questo capitolo, quali ad esempio la media e la varianza, ma è invece solo possibile riassumere i dati mediante una distribuzione di frequenze per le varie modalità della risposta.
12.10.3 Correlazione nulla
Un ultimo aspetto da mettere in evidenza a proposito della correlazione riguarda il fatto che la correlazione descrive la direzione e l’intensità della relazione lineare tra due variabili. Relazioni non lineari tra le variabili, anche sono molto forti, non vengono catturate dalla correlazione. È importante rendersi conto che una correlazione pari a zero non significa che non c’è relazione tra le due variabili, ma solo che tra esse non c’è una relazione lineare. Un esempio di questo fatto è fornito dalla figura 12.8.
library("datasauRus")
slant <- ggplot(datasaurus_dozen_wide, aes(x=slant_down_x,y=slant_down_y), colour=dataset)
# loads slant-pattern dataset of datasauRus package into data frame slant
slant <- slant +
geom_point() # as a scatter type geom
slant <- slant +
theme_void() # eliminates unwanted axis labels
slant <- slant +
theme(legend.position = "none",
panel.border = element_rect(colour = "black", fill=NA, size = 1),
plot.margin = margin(0,2,0,2), aspect.ratio = 1)
# removes legend, adds a border, adds margin space below, and specifies
# required aspect ratio
dino <- ggplot(datasaurus_dozen_wide, aes(x=dino_x,y=dino_y), colour=dataset) +
geom_point()
# loads dino-figure dataset of datasauRus package into data
#frame dino as a scatter type geom
dino <- dino +theme_void() # eliminates unwanted axis labels
dino <- dino +
theme(legend.position = "none",
panel.border = element_rect(colour = "black", fill=NA, size = 1),
plot.margin = margin(0,2,0,2), aspect.ratio = 1)
# removes legend, adds a border, adds margin space below, specifies
# required aspect ratio
slant + dino
Figura 12.8: Due insiemi di dati (fittizi) per i quali i coefficienti di correlazione di Pearson sono entrambi 0. Ma questo non significa che non vi sia alcuna relazione tra le variabili.
Conclusioni
La prima fase dell’analisi dei dati è sicuramente quella che ci porta a riassumere i dati mediante gli strumenti della statistica descrittiva. Ci sono diverse domande che vengono affrontate in questa fase: qual è la distribuzione delle variabili di interesse? Quali relazioni a coppie si possono osservare nel campione? Ci sono delle osservazioni ‘anomale,’ ovvero estremamente discrepanti rispetto alle altre, sia quando si esaminano le statistiche descrittive univariate (ovvero, quelle che riguardano le caratteristiche di una variabile presa singolarmente), sia quando vengono esaminate le statistiche bivariate (ovvero, le statistiche che descrivono l’associazione tra le variabili)? È importante avere ben chiare le idee su questi punti prima di procedere con qualsiasi procedura statistica di tipo inferenziale. Per rispondere alle domande che abbiamo elencato sopra, ed ad altre simili, è molto utile procedere con delle rappresentazioni grafiche dei dati. Dovrebbe essere chiaro che, quando disponiamo di grandi moli di dati (come è sempre il caso in psicologia), per fare questo è necessario usare un software statistico.
12.11 Esercizi
Scarica gli esercizi:
Download 14_descr_exercises.Rmd
Guarda le risposte solo dopo avere provato a rispondere a tutte le domande: