Capitolo 15 Il teorema di Bayes
Il teorema di Bayes ha un ruolo centrale nella statistica Bayesiana, anche se viene utilizzato anche dall’approccio frequentista. Prima di esaminare il teorema di Bayes introdurremo una sua componente, ovvero il teorema della probabilità totale.
15.1 Il teorema della probabilità totale
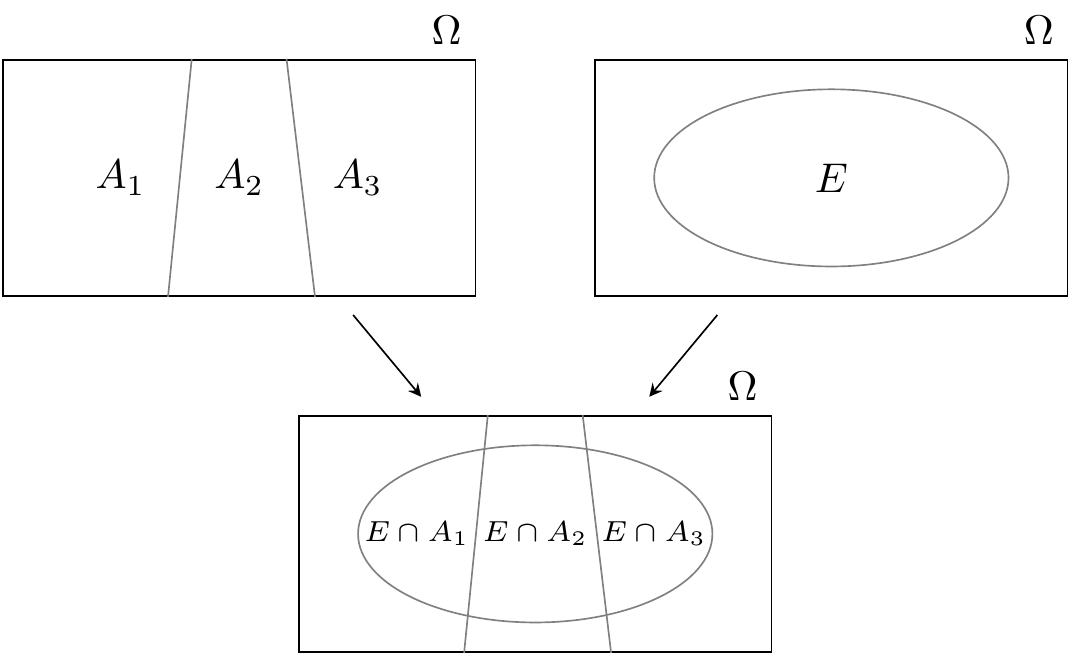
Il teorema della probabilità totale fa uso della legge della probabilità composta (14.3) per calcolare le probabilità di casi più complessi di quelli considerati fino ad ora. La notazione sembra complessa, ma l’idea sottostante è semplice. Discutiamo qui il teorema della probabilità totale considerando il caso di una partizione dello spazio campionario in tre sottoinsiemi. È facile estendere tale situazione al caso di una partizione in un qualunque numero di sottoinsiemi.
Il teorema della probabilità totale afferma che, se l’evento \(E\) è costituito da tutti gli eventi elementari in \(E \cap A_1\), \(E \cap A_2\) e \(E \cap A_3\), allora la probabilità \(P(E)\) è data dalla somma delle probabilità di queti tre eventi. Ciò è illustrato nella figura seguente.
Esercizio.
Si considerino tre urne, ciascuna delle quali contiene 100 palline:
- Urna 1: 75 palline rosse e 25 palline blu,
- Urna 2: 60 palline rosse e 40 palline blu,
- Urna 3: 45 palline rosse e 55 palline blu.
Una pallina viene estratta a caso da un’urna anch’essa scelta a caso. Qual è la probabilità che la pallina estratta sia di colore rosso?
Soluzione. Sia \(R\) l’evento “la pallina estratta è rossa” e sia \(U_i\) l’evento che corrisponde alla scelta dell’\(i\)-esima urna. Sappiamo che \[ P(R \mid U_1) = 0.75, \qquad P(R \mid U_2) = 0.60, \qquad P(R \mid U_3) = 0.45. \] Gli eventi \(U_1\), \(U_2\) e \(U_3\) costituiscono una partizione dello spazio campionario in quanto \(U_1\), \(U_2\) e \(U_3\) sono eventi mutualmente esclusivi ed esaustivi, \(P(U_1 \cup U_2 \cup U_3) = 1.0\). In base al teorema della probabilità totale, la probabilità di estrarre una pallina rossa è \[ \begin{aligned} P(R) &= P(R \mid U_1)P(U_1)+P(R \mid U_2)P(U_2)+P(R \mid U_3)P(U_3)\notag\\ &= 0.75 \cdot \frac{1}{3}+0.60 \cdot \frac{1}{3}+0.45 \cdot \frac{1}{3} =0.60.\notag \end{aligned} \]
Esercizio. Consideriamo un’urna che contiene 5 palline rosse e 2 palline verdi. Due palline vengono estratte, una dopo l’altra. Vogliamo sapere la probabilità dell’evento “la seconda pallina estratta è rossa.”
Soluzione. Lo spazio campionario è \(\Omega = \{RR, RV, VR, VV\}\). Chiamiamo \(R_1\) l’evento “la prima pallina estratta è rossa,” \(V_1\) l’evento “la prima pallina estratta è verde,” \(R_2\) l’evento “la seconda pallina estratta è rossa” e \(V_2\) l’evento “la seconda pallina estratta è verde.” Dobbiamo trovare \(P(R_2)\) e possiamo risolvere il problema usando il teorema della probabilità totale (15.2):
\[\begin{equation} \begin{aligned} P(R_2) &= P(R_2 \mid R_1) P(R_1) + P(R_2 \mid V_1)P(V_1)\notag\\ &= \frac{4}{6} \cdot \frac{5}{7} + \frac{5}{6} \cdot \frac{2}{7} = \frac{30}{42} = \frac{5}{7}.\notag \end{aligned} \end{equation}\] Se la prima estrazione è quella di una pallina rossa, nell’urna restano 4 palline rosse e due verdi, dunque, la probabilità che la seconda estrazione produca una pallina rossa è uguale a 4/6. La probabilità di una pallina rossa nella prima estrazione è 5/7. Se la prima estrazione è quella di una pallina verde, nell’urna restano 5 palline rosse e una pallina verde, dunque, la probabilità che la seconda estrazione produca una pallina rossa è uguale a 5/6. La probabilità di una pallina verde nella prima estrazione è 2/7.
15.2 Il teorema della probabilità delle cause
Il teorema di Bayes rappresenta uno dei fondamenti della teoria della probabilità e della statistica. Lo presentiamo qui considerando prima un caso specifico per poi descriverlo nella sua forma più generale.
Sia \(\{A_1, A_2\}\) una partizione dello spazio campionario \(\Omega\). Consideriamo un terzo evento \(E \subset \Omega\) con probabilità non nulla di cui si conoscono le probabilità condizionate rispetto ad \(A_1\) e a \(A_2\), ovvero \(P(E \mid A_1)\) e \(P(E \mid A_2)\). È chiaro per le ipotesi fatte che se si verifica \(E\) deve anche essersi verificato almeno uno degli eventi \(A_1\) e \(A_2\). Supponendo che si sia verificato l’evento \(E\), ci chiediamo: qual è la probabilità che si sia verificato \(A_1\) piuttosto che \(A_2\)?
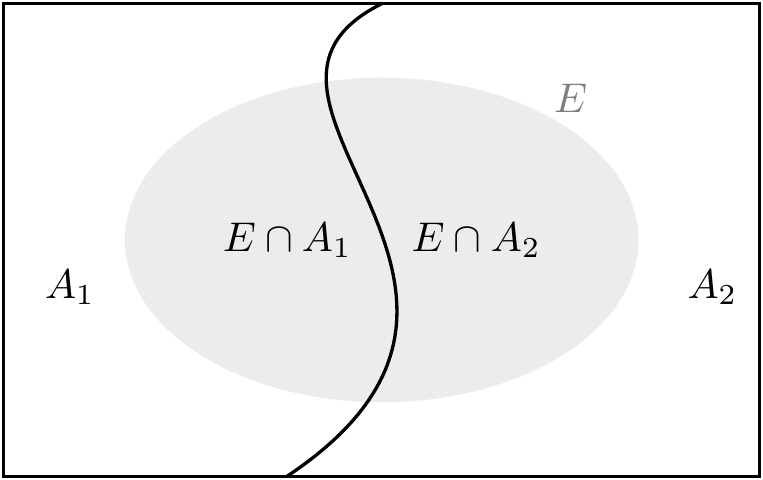
Per rispondere alla domanda precedente scriviamo: \[\begin{equation} \begin{aligned} P(A_1 \mid E) &= \frac{P(E \cap A_1)}{P(E)}\notag\\ &= \frac{P(E \mid A_1)P(A_1)}{P(E)}\notag.\end{aligned} \end{equation}\] Sapendo che \(E = (E \cap A_1) \cup (E \cap A_2)\) e che \(A_1\) e \(A_2\) sono eventi disgiunti, ovvero \(A_1 \cap A_2 = \emptyset\), ne segue che possiamo calcolare \(P(E)\) utilizzando il teorema della probabilità totale: \[\begin{equation} \begin{aligned} P(E) &= P(E \cap A_1) + P(E \cap A_2)\notag\\ &= P(E \mid A_1)P(A_1) + P(E \mid A_2)P(A_2).\notag \end{aligned} \end{equation}\] Sostituendo il risultato precedente nella formula della probabilità condizionata \(P(A_1 \mid E)\) otteniamo: \[\begin{equation} P(A_1 \mid E) = \frac{P(E \mid A_1)P(A_1)}{P(E \mid A_1)P(A_1) + P(E \mid A_2)P(A_2)}. \tag{15.3} \end{equation}\] La (15.3) si generalizza facilmente al caso di più di due eventi disgiunti, come indicato di seguito.
La formula (15.4) prende il nome di Teorema di Bayes e mostra che la conoscenza del verificarsi dell’evento \(E\) modifica la probabilità che abbiamo attribuito all’evento \(A_j\).
15.2.1 Aggiornamento Bayesiano
Consideriamo ora un’altra applicazione del teorema di Bayes che ci fa capire come l’applicazione di questo teorema ci consente di modificare una credenza a priori in maniera dinamica, via via che nuove evidenze vengono raccolta, in modo tale da formulare una credenza a posteriori la quale non è mai definitiva, ma può essere sempre aggiornata in base alle nuove evidenze disponibili. Questo processo si chiama aggiornamento Bayesiano.
Supponiamo che, per qualche strano errore di produzione, una fabbrica produca due tipi di monete. Il primo tipo di monete ha la caratteristica che, quando una moneta viene lanciata, la probabilità di osservare l’esito “testa” è 0.6. Per semplicità, sia \(\theta\) la probabilità di osservare l’esito “testa.” Per una moneta del primo tipo, dunque, \(\theta = 0.6\). Per una moneta del secondo tipo, invece, la probabilità di produrre l’esito “testa” è 0.4. Ovvero, \(\theta = 0.4\).
Noi possediamo una moneta, ma non sappiamo se è del primo tipo o del secondo tipo. Sappiamo solo che il 75% delle monete sono del primo tipo e il 25% sono del secondo tipo. Sulla base di questa conoscenza a priori – ovvero sulla base di una conoscenza ottenuta senza avere eseguito l’esperimento che consiste nel lanciare la moneta una serie di volte per osservare gli esiti prodotti – possiamo dire che la probabilità di una prima ipotesi, secondo la quale \(\theta = 0.6\), è 3 volte più grande della probabilità di una seconda ipotesi, secondo la quale \(\theta = 0.4\). Senza avere eseguito alcun esperimento casuale con la moneta, questo è quello che sappiamo.
Ora immaginiamo di lanciare una moneta due volte e di ottenere il risultato seguente: \(\{T, C\}\). Quello che ci chiediamo è: sulla base di questa evidenza, come cambiano le probabilità che associamo alle due ipotesi? In altre parole, ci chiediamo qual è la probabilità di ciascuna ipotesi alla luce dei dati che sono stati osservati: \(P(H \mid x)\), laddove \(x\) sono i dati osservati. Tale probabilità si chiama probabilità a posteriori. Inoltre, se confrontiamo le due ipotesi, ci chiediamo quale valore assuma il rapporto \(\frac{P(H_1 \mid x)}{P(H_2 \mid x)}\). Tale rapporto ci dice quanto è più probabile \(H_1\) rispetto ad \(H_2\), alla luce dei dati osservati. Infine, ci chiediamo come cambia il rapporto definito sopra, quando osserviamo via via nuovi risultati prodotti dal lancio della moneta.
Definiamo il problema in maniera più chiara. Conosciamo le probabilità a priori, ovvero \(P(H_1) = 0.75\) e \(P(H_1) = 0.25\). Quello che vogliamo conoscere sono le probabilità a posteriori \(P(H_1 \mid x)\) e \(P(H_2 \mid x)\).
Per trovare le probabilità a posteriori applichiamo il teorema di Bayes: \[ P(H_1 \mid x) = \frac{P(x \mid H_1) P(H_1)}{P(x)} = \frac{P(x \mid H_1) P(H_1)}{P(x \mid H_1) P(H_1) + P(x \mid H_2) P(H_2)} \] laddove lo sviluppo del denominatore deriva da un’applicazione del teorema della probabilità totale. Inoltre, \[ P(H_2 \mid x) = \frac{P(x \mid H_2) P(H_2)}{P(x \mid H_1) P(H_1) + P(x \mid H_2) P(H_2)}. \] Se consideriamo l’ipotesi \(H_1\) = “la probabilità di testa è 0.6,” allora la verosimiglianza dei dati \(\{T, C\}\), ovvero la probabilità di osservare questa specifica sequenza di T e C, è uguale a \(0.6 \times 0.4 = 0.24.\) Dunque, \(P(x \mid H_1) = 0.24\).
Se invece consideriamo l’ipotesi \(H_2\) = “la probabilità di testa è 0.4,” allora la verosimiglianza dei dati \(\{T, C\}\) è \(0.4 \times 0.6 = 0.24\), ovvero, \(P(x \mid H_2) = 0.24\). In base alle due ipotesi \(H_1\) e \(H_2\), dunque, i dati osservati hanno la medesima plausibilità di essere osservati. Per semplicità, calcoliamo anche \[ \begin{aligned} P(x) &= P(x \mid H_1) P(H_1) + P(x \mid H_2) P(H_2) = 0.24 \cdot 0.75 + 0.24 \cdot 0.25 = 0.24.\notag \end{aligned} \]
Le probabilità a posteriori diventano: \[ \begin{aligned} P(H_1 \mid x) &= \frac{P(x \mid H_1) P(H_1)}{P(x)} = \frac{0.24 \cdot 0.75}{0.24} = 0.75,\notag \end{aligned} \] \[ \begin{aligned} P(H_2 \mid x) &= \frac{P(x \mid H_2) P(H_2)}{P(x)} = \frac{0.24 \cdot 0.25}{0.24} = 0.25.\notag \end{aligned} \] Possiamo dunque concludere dicendo che, sulla base dei dati osservati, l’ipotesi \(H_1\) ha una probabilità 3 volte maggiore di essere vera dell’ipotesi \(H_2\).
È tuttavia possibile raccogliere più evidenze e, sulla base di esse, le probabilità a posteriori cambieranno. Supponiamo di lanciare la moneta una terza volta e di osservare croce. I nostri dati dunque sono \(\{T, C, C\}\).
Di conseguenza, \(P(x \mid H_1) = 0.6 \cdot 0.4 \cdot 0.4 = 0.096\) e \(P(x \mid H_2) = 0.4 \cdot 0.6 \cdot 0.6 = 0.144\). Ne segue che le probabilità a posteriori diventano: \[ \begin{aligned} P(H_1 \mid x) &= \frac{P(x \mid H_1) P(H_1)}{P(x)} = \frac{0.096 \cdot 0.75}{0.096 \cdot 0.75 + 0.144 \cdot 0.25} = 0.667,\notag \end{aligned} \] \[\begin{aligned} P(H_2 \mid x) &= \frac{P(x \mid H_2) P(H_2)}{P(x)} = \frac{0.144 \cdot 0.25}{0.096 \cdot 0.75 + 0.144 \cdot 0.25} = 0.333.\notag\end{aligned}\] In queste circostanze, le evidenze che favoriscono \(H_1\) nei confronti di \(H_2\) sono solo pari ad un fattore di 2.
Se otteniamo ancora croce in un quarto lancio della moneta, i nostri dati diventano: \(\{T, C, C, C\}\). Ripetendo il ragionamento fatto sopra, \(P(x \mid H_1) = 0.6 \cdot 0.4 \cdot 0.4 \cdot 0.4 = 0.0384\) e \(P(x \mid H_2) = 0.4 \cdot 0.6 \cdot 0.6 \cdot 0.6 = 0.0864\).
Dunque \[ \begin{aligned} P(H_1 \mid x) &= \frac{0.0384 \cdot 0.75}{0.0384 \cdot 0.75 + 0.0864 \cdot 0.25} = 0.571,\notag \end{aligned} \] \[ \begin{aligned} P(H_2 \mid x) &= \frac{0.0864 \cdot 0.25}{0.0384 \cdot 0.75 + 0.0864 \cdot 0.25} = 0.429.\notag \end{aligned} \] e le evidenze a favore di \(H_1\) si riducono a 1.33. Se si ottenesse un altro esito croce in un sesto lancio della moneta, l’ipotesi \(H2\) diventerebbe più probabile dell’ipotesi \(H_1\).
In conclusione, questo esercizio ci fa capire come sia possibile aggiornare le nostre credenze sulla base delle evidenze disponibili, ovvero come sia possibile passare da un grado di conoscenza del mondo a priori a una conoscenza a posteriori. Se prima di lanciare la moneta ritenevamo che l’ipotesi \(H_1\) fosse tre volte più plausibile dell’ipotesi \(H_2\), dopo avere osservato uno specifico campione di dati siamo giunti alla conclusione opposta. Il processo di aggiornamento Bayesiano, dunque, ci fornisce un metodo per modificare il livello di fiducia in una data ipotesi, alla luce di nuove informazioni.
Conclusioni
Il teorema di Bayes costituisce il fondamento dell’approccio più moderno della statistica, quello appunto detto Bayesiano. Chi usa il teorema di Bayes non è, solo per questo motivo, “bayesiano.” Ci vuole ben altro. Ci vuole un modo diverso per intendere il significato della probabilità e un modo diverso per intendere gli obiettivi dell’inferenza statistica. L’approccio bayesiano è stato, negli scorsi decenni, un approccio piuttosto dogmatico a questi temi e, a causa di ciò, è stato considerato da alcuni come un metodo un po’ troppo lontano dall’atteggiamento critico e non dogmatico che costituisce il fondamento della comunità scientifica. In anni recenti, questi aspetti più “ruvidi” dell’approccio bayesiano sono stati abbandonati e una gran parte della comunità scientifica riconosce all’approccio bayesiano il merito di consentire lo sviluppo di modelli anche molto complessi senza, d’altra parte, richiedere conoscenze matematiche troppo avanzate all’utente. Per questa ragione l’approccio bayesiano sta prendendo sempre più piede, anche in psicologia. Un introduzione a questi temi sarà presentata nell’ultima parte di queste dispense.