37. Modello LCS univariato#
I Latent Growth Model descrivono la variabile \(Y\) al tempo \(t\). I Latent Change Score Models (LCSM; McArdle, 2001, 2009; McArdle & Hamagami, 2001) rendono esplicito il cambiamento di \(Y\) da \(t-1\) a \(t\). Questo cambiamento nel paradigma dell’analisi statistica costringe l’analista a focalizzarsi sull’aspettativa del cambiamento in \(Y\). I modelli LCS vengono utilizzati per studiare come i costrutti cambiano nel tempo e possono essere usati per stimare la traiettoria di sviluppo di un costrutto o per indagare l’associazione tra i cambiamenti di due costrutti nel tempo.
I modelli LCS sono stati utilizzati nella psicologia dello sviluppo per mostrare diversi effetti. Ad esempio, che il vocabolario influisce sulla comprensione della lettura, che le persone con dislessia mostrano minori benefici intellettuali dalla lettura, che l’addestramento cognitivo si generalizza oltre il livello degli elementi all’abilità cognitiva e che le abilità cognitive di base come il ragionamento e il vocabolario mostrano mutui benefici nel tempo.
In termini statistici, i modelli di cambiamento latente (LCS) si concentrano sul cambiamento nei costrutti dipendenti dal tempo piuttosto che sui punteggi osservati. Questo approccio consente di studiare direttamente il cambiamento intra-individuale attraverso una modellizzazione statistica adeguata. Analogamente a un test t per dati accoppiati, nei modelli LCS il punteggio di cambiamento latente rimuove la varianza dovuta alle differenze inter-individuali e fornisce una misura del cambiamento all’interno dell’individuo tra diverse rilevazioni temporali [CPM+13].
La modellizzazione del punteggio di cambiamento latente si basa sui concetti della teoria classica dei test, ovvero assume che il punteggio osservato (X) di un individuo (i) in un particolare momento (t) possa essere espresso come la somma del “punteggio vero” dell’individuo (lx) e del “punteggio unico / residuo” (u) dell’individuo in quel momento:
I modelli di cambiamento latente (LCS) scompongono i punteggi osservati per testare ipotesi sui cambiamenti nei costrutti latenti riducendo l’effetto dell’errore di misura. I modelli LCS stimano una variabile latente che cattura il cambiamento nei “punteggi veri” latenti tra diversi punti temporali. Combinando i modelli di curva di crescita latente e i modelli cross-lag autoregressivi, i modelli LCS forniscono un’analisi dettagliata dei cambiamenti intra-personali in uno o più costrutti nel tempo. Un approccio comune è quello di comprendere prima le traiettorie individuali di ogni costrutto in un modello LCS univariato e poi combinare entrambi i modelli per esaminare le loro relazioni in un modello LCS bivariato. In questo capitolo esamineremo i modelli LCS univariati; nel prossimo capitolo ci occuperemo del caso bivariato.
Iniziamo importiamo i pacchetti necessari.
source("_common.R")
suppressPackageStartupMessages({
library("lavaan")
library("semPlot")
library("knitr")
library("markdown")
library("patchwork")
library("psych")
library("DT")
library("kableExtra")
library("lme4")
library("lcsm")
library("tidyr")
library("stringr")
library("reshape2")
})
set.seed(42)
37.1. Un singolo indicatore in due rilevazioni temporali#
Iniziamo con il caso più semplice, ovvero quello di una singola misura osservata in due momenti nel tempo per un campione di individui. Verrà qui discusso un esempio presentato da Kievit et al. [KBZ+18]. Supponiamo dunque che un ricercatore studi una variabile psicologica la quale viene osservata in due momenti del tempo (T1 e T2) in una popolazione di interesse. Il modo tradizionale con cui si indaga se i punteggi di un gruppo di individui sono aumentati o diminuiti tra T1 e T2 è quello di eseguire un test t di Student per dati appaiati. Con poche modifiche, il modello LCS ci consente di andare oltre questo quadro di analisi tradizionale.
Iniziamo a simulare i dati usando lo script fornito da Kievit et al. [KBZ+18].
samplesize <- 100
ULCS_simulate <- '
##### The following lines specify the core assumptions of the LCS
##### and should not generally be modified
COG_T2 ~ 1*COG_T1 # Fixed regression of COG_T2 on COG_T1
dCOG1 =~ 1*COG_T2 # Fixed regression of dCOG1 on COG_T2
COG_T2 ~ 0*1 # This line constrains the intercept of COG_T2 to 0
COG_T2 ~~ 0*COG_T2 # This fixes the variance of the COG_T2 to 0
###### The following five parameters will be estimated in the model.
###### Values can be modified manually to examine the effect on the model
dCOG1 ~ 4*1 # This fixes the intercept of the change score to 10
COG_T1 ~ 10*1 # This fixes the intercept of COG_T1 to 50
dCOG1 ~~ 5*dCOG1 # This fixes the variance of the change scores to 5.
COG_T1 ~~ 8*COG_T1 # This fixes the variance of the COG_T1 to 8.
dCOG1 ~ -0.1*COG_T1 # This fixes the self-feedback parameter to -0.1.
'
set.seed(42)
simdatULCS <- simulateData(ULCS_simulate, sample.nobs = samplesize, meanstructure = TRUE)
print(colMeans(simdatULCS)) # sanity check the means
COG_T2 COG_T1
12.81156 10.02172
I valori precedenti indicano le medie dei punteggi di un ipotetico test cognitivo nei momenti T1 e T2 calcolate sulla base dei risultati di 100 soggetti.
Il modello LCS viene formulato nel modo seguente.
ULCS <- '
COG_T2 ~ 1*COG_T1 # Fixed regression of COG_T2 on COG_T1
dCOG1 =~ 1*COG_T2 # Fixed regression of dCOG1 on COG_T2
COG_T2 ~ 0*1 # This line constrains the intercept of COG_T2 to 0
COG_T2 ~~ 0*COG_T2 # This fixes the variance of the COG_T2 to 0
dCOG1 ~ 1 # This estimates the intercept of the change scores
COG_T1 ~ 1 # This estimates the intercept of COG_T1
dCOG1 ~~ dCOG1 # This estimates the variance of the change scores
COG_T1 ~~ COG_T1 # This estimates the variance of COG_T1
dCOG1 ~ COG_T1 # This estimates the self-feedback parameter
'
Il corrispondente diagramma di percorso è fornito nella figura seguente.
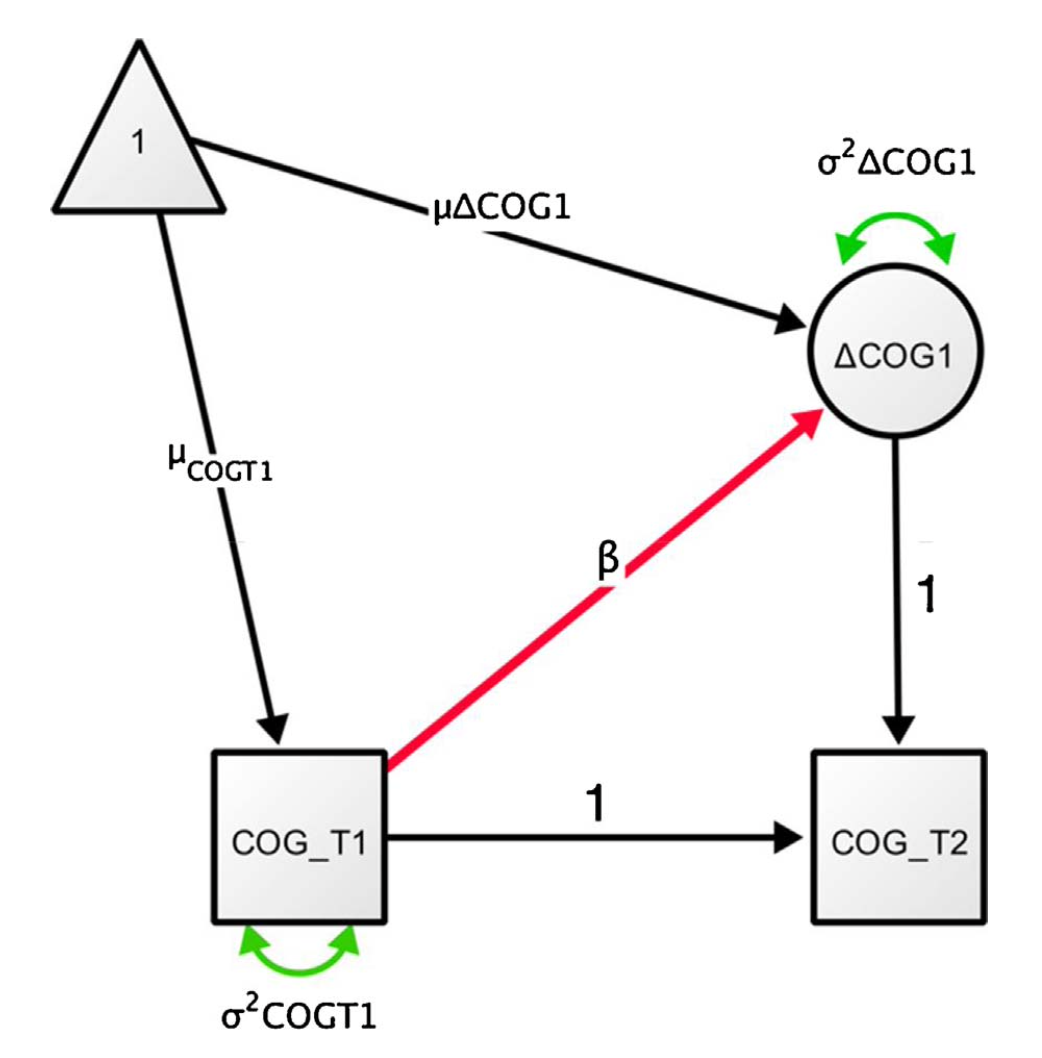
Fig. 37.1 Diagramma di percorso semplificato di un LCSM univariato. La variabile COG viene misurata in due momenti (COG_T1 e COG_T2). Il cambiamento (ΔCOG1) tra i due momenti viene modellato come una variabile latente.#
COG_T1 e COG_T2 sono i punteggi osservati nei due momenti temporali; \(\delta\)COG1 rappresenta la differenza tra i punteggi latenti nei due momenti temporali.
Dato che il coefficiente parziale di regressione da COG_T1 a COG_T2 è fissato a 1, la media di COG_T2 è data da \(\mu_{COGT1} + \mu_\Delta{COG1}\). In altri termini, la differenza tra i punteggi latenti COG tra i due momenti temporali è uguale a \(\mu_\Delta{COG1}\). Il framework SEM consente di definire un fattore per il cambiamento del punteggio latente ΔCOG1, il quale viene identificato a partire dal punto temporale 2 con una saturazione fattoriale fissata a 1. Facendo ciò si crea un fattore latente che cattura il cambiamento tra il tempo 1 e il tempo 2.
Inoltre, il modello LCS aggiunge un parametro di regressione β al punteggio di cambiamento, che consente di indagare se il grado di cambiamento dipende dai punteggi al tempo 1 come segue:
Con questo modello possiamo rispondere a tre domande. La prima domanda è se c’è un cambiamento medio affidabile da T1 a T2. Questo cambiamento è catturato dalla media del fattore del cambiamento latente, μΔCOG1. Sotto ipotesi relativamente semplici, questo test è equivalente a un test t di Student per dati appaiati [CPM+13]. Tuttavia, anche questa semplice implementazione del modello LSC produce due ulteriori parametri di notevole interesse. Innanzitutto, ora possiamo stimare la varianza nel fattore di cambiamento, \(σ^2ΔCOG1\), che cattura la misura in cui gli individui differiscono nel cambiamento che manifestano nel tempo. In secondo luogo, possiamo specificare una covarianza o un parametro autoregressivo β che cattura la misura in cui il cambiamento dipende o è proporzionale ai punteggi al tempo uno (questo parametro può anche essere specificato come covarianza se desiderato. Se viene incluso un parametro di regressione, il cambiamento medio deve essere interpretato condizionatamente al percorso di regressione; una covarianza stima il cambiamento medio “grezzo”).
Adattiamo il modello specificato ai dati dell’esempio.
fitULCS <- lavaan(ULCS, data=simdatULCS, estimator='mlr', fixed.x=FALSE, missing='fiml')
summary(fitULCS, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE) |>
print()
lavaan 0.6.15 ended normally after 37 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 5
Number of observations 100
Number of missing patterns 1
Model Test User Model:
Standard Scaled
Test Statistic 0.000 0.000
Degrees of freedom 0 0
Model Test Baseline Model:
Test statistic 105.669 85.223
Degrees of freedom 1 1
P-value 0.000 0.000
Scaling correction factor 1.240
User Model versus Baseline Model:
Comparative Fit Index (CFI) 1.000 1.000
Tucker-Lewis Index (TLI) 1.000 1.000
Robust Comparative Fit Index (CFI) 1.000
Robust Tucker-Lewis Index (TLI) 1.000
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -461.157 -461.157
Loglikelihood unrestricted model (H1) -461.157 -461.157
Akaike (AIC) 932.314 932.314
Bayesian (BIC) 945.339 945.339
Sample-size adjusted Bayesian (SABIC) 929.548 929.548
Root Mean Square Error of Approximation:
RMSEA 0.000 NA
90 Percent confidence interval - lower 0.000 NA
90 Percent confidence interval - upper 0.000 NA
P-value H_0: RMSEA <= 0.050 NA NA
P-value H_0: RMSEA >= 0.080 NA NA
Robust RMSEA 0.000
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.000
P-value H_0: Robust RMSEA <= 0.050 NA
P-value H_0: Robust RMSEA >= 0.080 NA
Standardized Root Mean Square Residual:
SRMR 0.000 0.000
Parameter Estimates:
Standard errors Sandwich
Information bread Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
dCOG1 =~
COG_T2 1.000 2.038 0.590
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
COG_T2 ~
COG_T1 1.000 1.000 0.839
dCOG1 ~
COG_T1 -0.038 0.064 -0.582 0.560 -0.018 -0.053
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.COG_T2 0.000 0.000 0.000
.dCOG1 3.166 0.648 4.886 0.000 1.554 1.554
COG_T1 10.022 0.290 34.604 0.000 10.022 3.460
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.COG_T2 0.000 0.000 0.000
.dCOG1 4.140 0.733 5.645 0.000 0.997 0.997
COG_T1 8.387 1.305 6.426 0.000 8.387 1.000
R-Square:
Estimate
COG_T2 1.000
dCOG1 0.003
Il cambiamento nel punteggio latente tra i momenti T1 e T2 è stimato essere uguale a 3.166 (SE = 0.648). Questo valore può essere messo in relazione alla differenza tra le medie dei punteggi in due momenti temporali che viene calcolata da un test t di Student per dati appaiati. Si noti però che, mentre nel caso del test t la differenza riguarda i punteggi osservati, nei modelli LSC essa descrive la variazione tra i punteggi latenti nei momenti T1 e T2.
Il coefficiente 7.350 (SE = 0.494) stima la varianza con la quale gli individui differiscono nel cambiamento che manifestano nel tempo.
Infine, il coefficiente -0.097 (SE = 0.036) stima la componente autoregressiva dal tempo T1 al tempo T2.
Generiamo il diagramma di percorso con l’ausilio di semPaths.
semPaths(fitULCS, what = "path", whatLabels = "par")
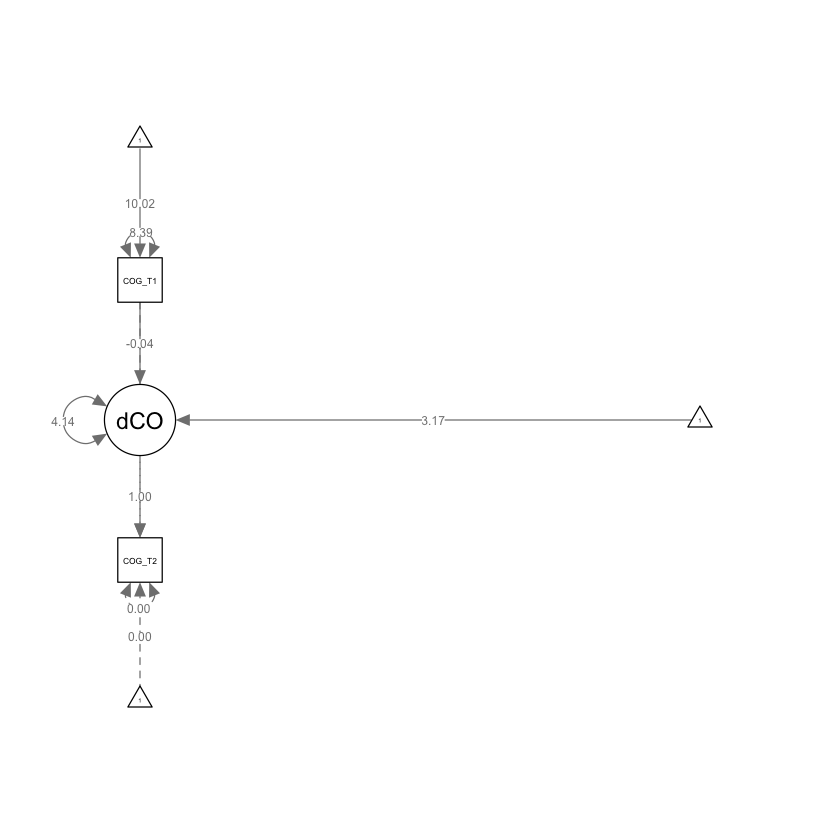
37.2. Indicatori multipli in due rilevazioni temporali#
Consideriamo ora il caso in cui abbiamo indicatori multipli in due momenti nel tempo. Iniziamo con simulare i dati usando lo script fornito dagli autori.
samplesize <- 100
#Simulate data for a Univariate Latent Change Score model.
MILCS_simulate <- '
#### The following two lines specify the measurement model for multiple indicators (X1-X3)
#### measured on two occasions (T1-T2)
COG_T1=~.8*T1X1+.9*T1X2+.7*T1X3 # This specifies the measurement model for COG_T1
COG_T2=~.8*T2X1+.9*T2X2+.7*T2X3 # This specifies the measurement model for COG_T2
##### The following lines specify the core assumptions of the LCS
##### and should not generally be modified
COG_T2 ~ 1*COG_T1 # Fixed regression of COG_T2 on COG_T1
dCOG1 =~ 1*COG_T2 # Fixed regression of dCOG1 on COG_T2
COG_T2 ~ 0*1 # This line constrains the intercept of COG_T2 to 0
COG_T2 ~~ 0*COG_T2 # This fixes the variance of the COG_T2 to 0
T1X1~0*1 # This fixes the intercept of X1 to 0
T1X2~1*1 # This fixes the intercept of X2 to 1
T1X3~.5*1 # This fixes the intercept of X3 to 0.5
T2X1~0*1 # This fixes the intercept of X1 to 0
T2X2~1*1 # This fixes the intercept of X2 to 1
T2X3~.5*1 # This fixes the intercept of X3 to 0.5
###### The following five parameters will be estimated in the model.
###### Values can be modified manually to examine the effect on the model
dCOG1 ~ 10*1 # This fixes the intercept of the change score to 10
COG_T1 ~ 50*1 # This fixes the intercept of COG_T1 to 50.
dCOG1 ~~ 5*dCOG1 # This fixes the variance of the change scores to 5.
COG_T1 ~~ 8*COG_T1 # This fixes the variance of the COG_T1 to 8.
dCOG1 ~ -0.1*COG_T1 # This fixes the self-feedback parameter to -0.1.
'
Simuliamo i dati.
set.seed(123)
simdatMILCS <- simulateData(MILCS_simulate, sample.nobs = samplesize, meanstructure = TRUE)
Queste sono le medie delle tre variabili nei due momenti temporali.
print(colMeans(simdatMILCS))
T1X1 T1X2 T1X3 T2X1 T2X2 T2X3
39.66328 45.74262 35.16919 43.92156 50.35134 38.76447
Definiamo il modello LCS per indicatori multipli e due momenti temporali (il codice è fornito da Kievit et al. [KBZ+18]).
MILCS <- '
COG_T1 =~ 1*T1X1+T1X2+T1X3 # This specifies the measurement model for COG_T1
COG_T2 =~ 1*T2X1+equal("COG_T1=~T1X2")*T2X2+equal("COG_T1=~T1X3")*T2X3 # This specifies the measurement model for COG_T2 with the equality constrained factor loadings
COG_T2 ~ 1*COG_T1 # Fixed regression of COG_T2 on COG_T1
dCOG1 =~ 1*COG_T2 # Fixed regression of dCOG1 on COG_T2
COG_T2 ~ 0*1 # This line constrains the intercept of COG_T2 to 0
COG_T2 ~~ 0*COG_T2 # This fixes the variance of the COG_T2 to 0
dCOG1 ~ 1 # This estimates the intercept of the change score
COG_T1 ~ 1 # This estimates the intercept of COG_T1
dCOG1 ~~ dCOG1 # This estimates the variance of the change scores
COG_T1 ~~ COG_T1 # This estimates the variance of the COG_T1
dCOG1~COG_T1 # This estimates the self-feedback parameter
T1X1~~T2X1 # This allows residual covariance on indicator X1 across T1 and T2
T1X2~~T2X2 # This allows residual covariance on indicator X2 across T1 and T2
T1X3~~T2X3 # This allows residual covariance on indicator X3 across T1 and T2
T1X1~~T1X1 # This allows residual variance on indicator X1
T1X2~~T1X2 # This allows residual variance on indicator X2
T1X3~~T1X3 # This allows residual variance on indicator X3
T2X1~~equal("T1X1~~T1X1")*T2X1 # This allows residual variance on indicator X1 at T2
T2X2~~equal("T1X2~~T1X2")*T2X2 # This allows residual variance on indicator X2 at T2
T2X3~~equal("T1X3~~T1X3")*T2X3 # This allows residual variance on indicator X3 at T2
T1X1~0*1 # This constrains the intercept of X1 to 0 at T1
T1X2~1 # This estimates the intercept of X2 at T1
T1X3~1 # This estimates the intercept of X3 at T1
T2X1~0*1 # This constrains the intercept of X1 to 0 at T2
T2X2~equal("T1X2~1")*1 # This estimates the intercept of X2 at T2
T2X3~equal("T1X3~1")*1 # This estimates the intercept of X3 at T2
'
Adattiamo il modello ai dati.
fitMILCS <- lavaan(MILCS, data=simdatMILCS, estimator='mlr', fixed.x=FALSE, missing='fiml')
Esaminiamo la soluzione.
summary(fitMILCS, fit.measures = TRUE, standardized = TRUE, rsquare = TRUE) |>
print()
lavaan 0.6.15 ended normally after 65 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 22
Number of equality constraints 7
Number of observations 100
Number of missing patterns 1
Model Test User Model:
Standard Scaled
Test Statistic 12.687 12.026
Degrees of freedom 12 12
P-value (Chi-square) 0.392 0.444
Scaling correction factor 1.055
Yuan-Bentler correction (Mplus variant)
Model Test Baseline Model:
Test statistic 615.947 602.011
Degrees of freedom 15 15
P-value 0.000 0.000
Scaling correction factor 1.023
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.999 1.000
Tucker-Lewis Index (TLI) 0.999 1.000
Robust Comparative Fit Index (CFI) 1.000
Robust Tucker-Lewis Index (TLI) 1.001
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -1087.543 -1087.543
Scaling correction factor 0.658
for the MLR correction
Loglikelihood unrestricted model (H1) -1081.200 -1081.200
Scaling correction factor 1.005
for the MLR correction
Akaike (AIC) 2205.086 2205.086
Bayesian (BIC) 2244.164 2244.164
Sample-size adjusted Bayesian (SABIC) 2196.790 2196.790
Root Mean Square Error of Approximation:
RMSEA 0.024 0.005
90 Percent confidence interval - lower 0.000 0.000
90 Percent confidence interval - upper 0.106 0.100
P-value H_0: RMSEA <= 0.050 0.608 0.661
P-value H_0: RMSEA >= 0.080 0.171 0.134
Robust RMSEA 0.000
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.104
P-value H_0: Robust RMSEA <= 0.050 0.673
P-value H_0: Robust RMSEA >= 0.080 0.143
Standardized Root Mean Square Residual:
SRMR 0.038 0.038
Parameter Estimates:
Standard errors Sandwich
Information bread Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
COG_T1 =~
1.000 2.179 0.919
(.p2.) 1.106 0.033 33.436 0.000 2.409 0.933
(.p3.) 0.817 0.029 27.789 0.000 1.780 0.865
COG_T2 =~
1.000 2.498 0.936
(COG_T1=~T1X2) 1.106 0.033 33.436 0.000 2.762 0.948
(COG_T1=~T1X3) 0.817 0.029 27.789 0.000 2.040 0.892
dCOG1 =~
1.000 0.692 0.692
Regressions:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
COG_T2 ~
COG_T1 1.000 0.872 0.872
dCOG1 ~
COG_T1 -0.158 0.105 -1.500 0.134 -0.199 -0.199
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.T1X1 ~~
.T2X1 -0.033 0.140 -0.237 0.813 -0.033 -0.038
.T1X2 ~~
.T2X2 -0.117 0.136 -0.857 0.392 -0.117 -0.136
.T1X3 ~~
.T2X3 -0.006 0.123 -0.052 0.959 -0.006 -0.006
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.COG_T2 0.000 0.000 0.000
.dCOG1 10.511 4.119 2.552 0.011 6.077 6.077
COG_T1 39.667 0.232 170.663 0.000 18.208 18.208
.T1X1 0.000 0.000 0.000
.T1X2 (.26.) 1.842 1.384 1.331 0.183 1.842 0.714
.T1X3 (.27.) 2.828 1.238 2.284 0.022 2.828 1.374
.T2X1 0.000 0.000 0.000
.T2X2 (T1X2) 1.842 1.384 1.331 0.183 1.842 0.632
.T2X3 (T1X3) 2.828 1.238 2.284 0.022 2.828 1.236
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.COG_T2 0.000 0.000 0.000
.dCOG1 2.873 0.444 6.471 0.000 0.960 0.960
COG_T1 4.746 0.742 6.397 0.000 1.000 1.000
.T1X1 (.19.) 0.875 0.129 6.806 0.000 0.875 0.156
.T1X2 (.20.) 0.856 0.139 6.143 0.000 0.856 0.129
.T1X3 (.21.) 1.068 0.128 8.356 0.000 1.068 0.252
.T2X1 (T1X1) 0.875 0.129 6.806 0.000 0.875 0.123
.T2X2 (T1X2) 0.856 0.139 6.143 0.000 0.856 0.101
.T2X3 (T1X3) 1.068 0.128 8.356 0.000 1.068 0.204
R-Square:
Estimate
COG_T2 1.000
dCOG1 0.040
T1X1 0.844
T1X2 0.871
T1X3 0.748
T2X1 0.877
T2X2 0.899
T2X3 0.796
Il coefficiente 10.511 (SE = 4.119) indica la variazione stimata nel costrutto identificato dai tre indicatori X1, X2, X3 tra i due momenti T1 e T2. Il coefficiente 2.873 (SE = 0.444) descrive la varianza del cambiamento del valore del costrutto nel tempo tra gli individui. Il coefficiente -0.158 (SE = 0.105) stima la componente autoregressiva del cambiamento.
Generiamo il diagramma di percorso.
semPaths(fitMILCS, what = "path", whatLabels = "par")
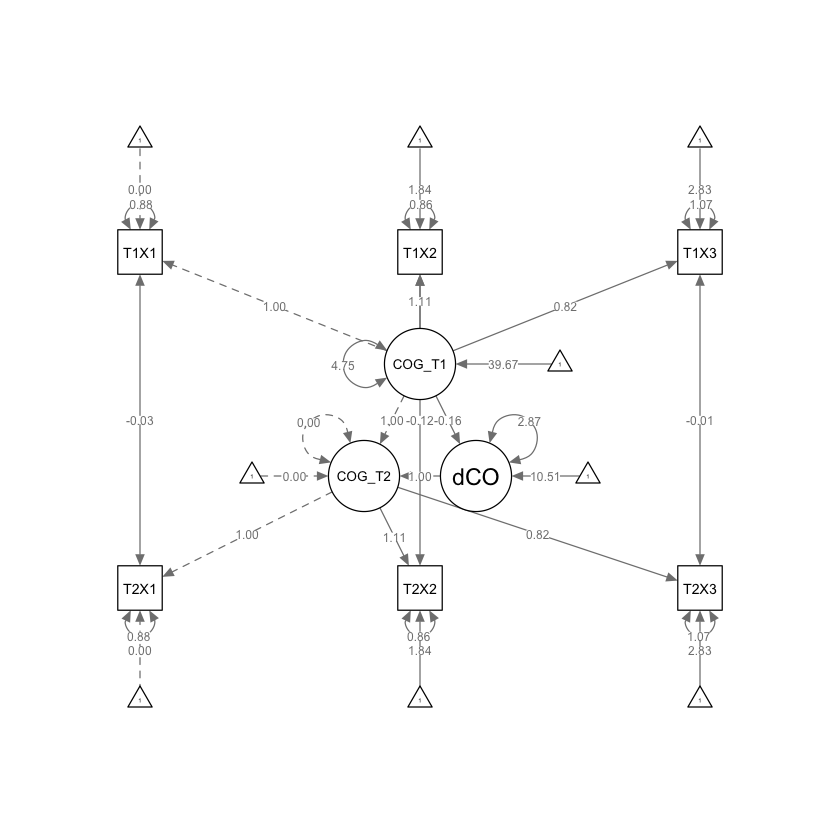
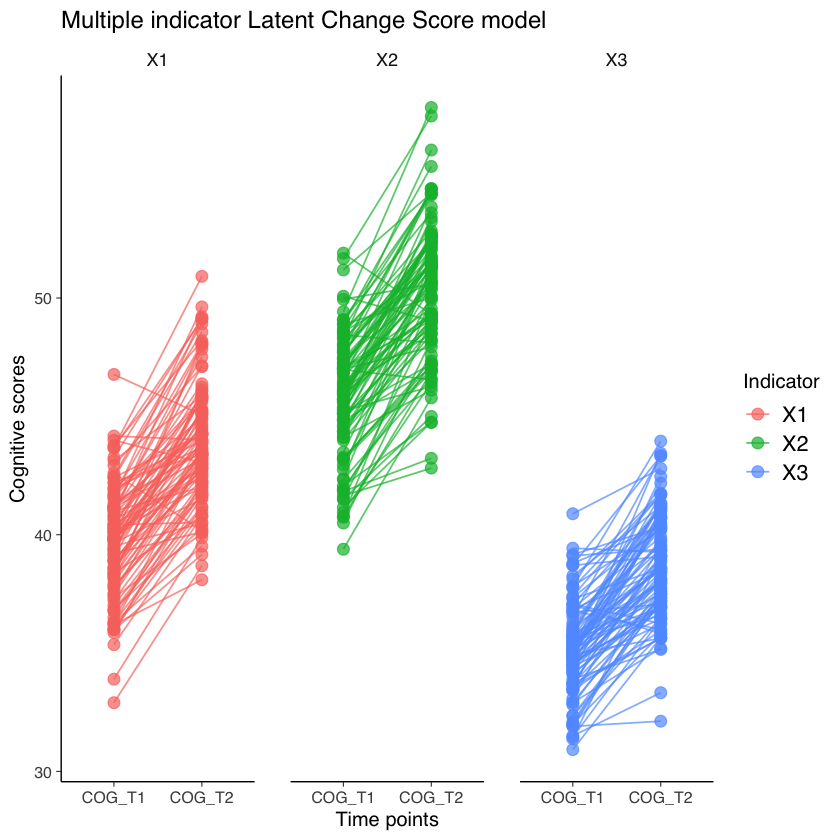
Esaminiamo la variazione dei punteggi latenti dei soggetti.
id = factor(1:samplesize)
plotdattemp = data.frame(
c(simdatMILCS$T1X1, simdatMILCS$T1X2, simdatMILCS$T1X3),
c(simdatMILCS$T2X1, simdatMILCS$T2X2, simdatMILCS$T2X3),
as.factor(c(id, id, id)),
c(
rep("X1", times = samplesize),
rep("X2", times = samplesize),
rep("X3", times = samplesize)
)
)
colnames(plotdattemp) <- c('COG_T1', 'COG_T2','id','Indicator')
plotdat <- melt(plotdattemp,by='id')
ggplot(plotdat, aes(variable, value, group = id, col = Indicator)) +
geom_point(size = 3, alpha = .7) +
geom_line(alpha = .7) +
ggtitle("Multiple indicator Latent Change Score model") +
ylab("Cognitive scores") +
xlab("Time points") +
facet_grid(~Indicator)
Using id, Indicator as id variables
37.3. Modello di cambiamento duale#
In questo secondo esempio fornito da [WTKovsirE22] estenderemo l’approccio illustrato in precedenza. Useremo inoltre le funzionalità del pacchetto R lcsm fornito dagli stessi autori per specificare il modello LCS univariato in un caso più complesso di quello esaminato nel primo esempio.
Il modello LCS univariato descritto ora si pone il problema di descrivere i cambiamenti degli individui (\(i\)) in un costrutto (\(X\)) in una serie di momenti del tempo (\(t\)). La figura successiva riporta il diagramma di percorso fornito da Wiedemann et al. [WTKovsirE22].
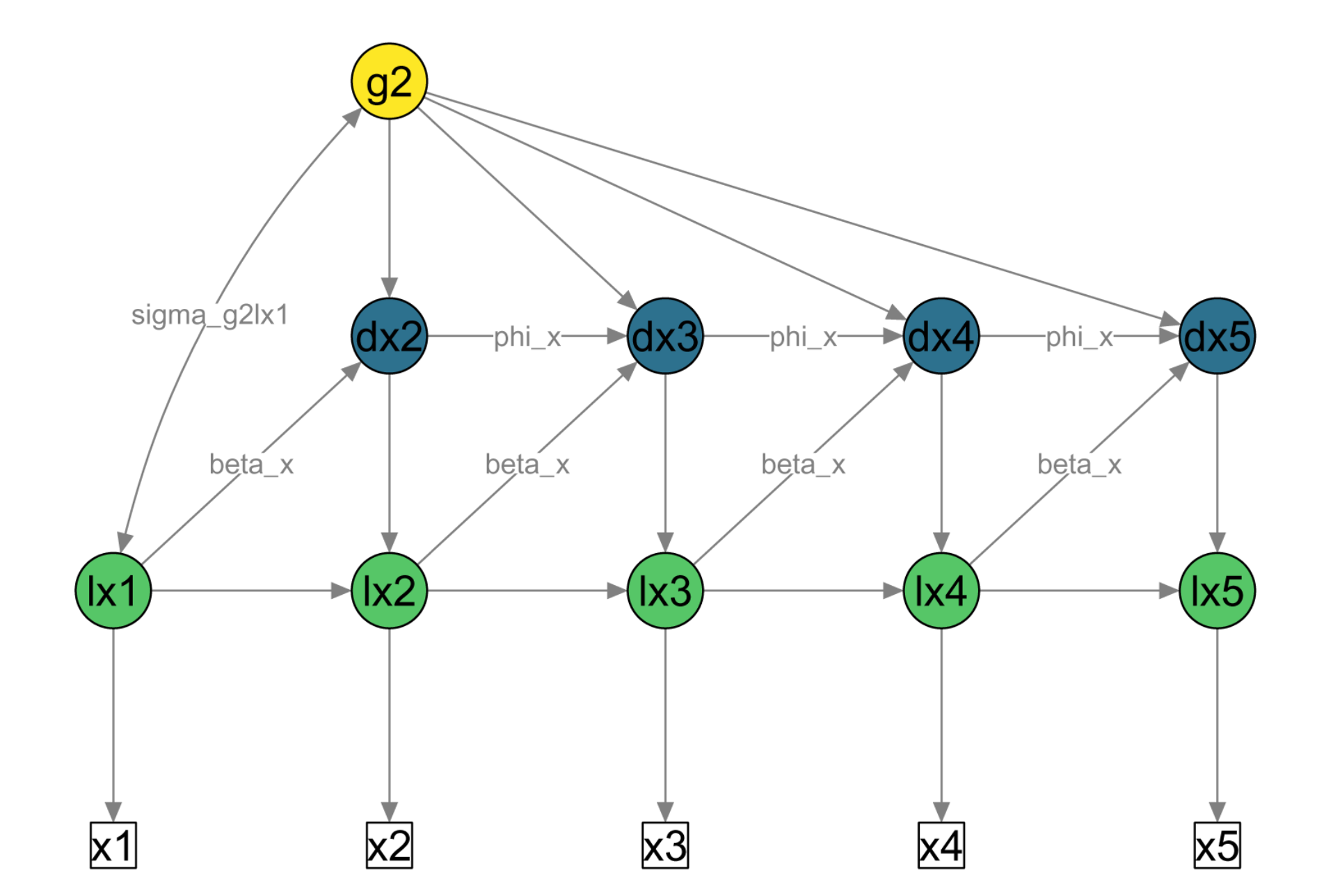
Fig. 37.2 Diagramma di percorso semplificato di LCSM univariato. Quadrati bianchi = punteggi osservati sulla variabile \(x\) nei punti temporali da 1 a 5; cerchi verdi = punteggi veri latenti (prefisso ‘l’); cerchi blu = punteggi di cambiamento latenti (prefisso ‘d’); cerchio giallo = fattore di cambiamento latente costante. Frecce direzionali = regressioni; frecce bidirezionali = covarianze. Parametro beta_x = fattore di cambiamento proporzionale; parametro phi_x = autoregressione dei punteggi di cambiamento; parametro sigma_g2lx1 = covarianza del fattore di cambiamento (g2) con il punteggio vero iniziale (lx1). I punteggi unici (\(ux_t\)) e le varianze uniche (\(σ^2_{ux}\)) non sono mostrati nella figura per semplicità.#
Come indicato in precedenza, i modelli LCS descrivono il cambiamento di un costrutto nel tempo mediante tre parametri:
un parametro di cambiamento costante (\(α_x \cdot s_{xi}\)),
un parametro di cambiamento proporzionale (\(β_x \cdot x_{[t−1]i}\)),
un effetto autoregressivo dei punteggi di cambiamento (\(ϕ_x \cdot ∆x_{[t−1]i}\)).
Il cambiamento in un costrutto (X) in un punto temporale specifico (t) è specificato dalla seguente equazione che include i tre parametri precedenti:
Il parametro di cambiamento costante (\(α_x\)) è simile al cambiamento in un modello lineare, perché ha lo stesso effetto su tutti i punteggi di cambiamento (si vedano i percorsi identici che conducono da
g2a ciascun punteggio di cambiamentodx2adx5nella figura precedente).Il parametro di cambiamento proporzionale (\(β_x\)) descrive se il “punteggio di cambiamento” al tempo (\(t\)) è determinato dal “punteggio vero” dello stesso costrutto al punto temporale precedente (\(t-1\)) – si vedano i percorsi etichettati
beta_xnella figura. Il cambiamento viene detto “proporzionale” perché i cambiamenti previsti sono proporzionali allo stato del punteggio vero nel momento temporale precedente.Le autoregressioni dei punteggi di cambiamento descrivono se un dato punteggio di cambiamento sono determinate dal punteggio di cambiamento precedente (si vedano i percorsi etichettati
phi_xnella figura).
Si noti che in questo esempio tutti i parametri sono vincolati ad essere uguali nel tempo.
Questo modello viene chiamato modello di cambiamento duale ed è il modello LCS più comunemente usato per dati longitudinali. Questo modello include quello che viene spesso definito come un effetto maturativo (\(g2_i\)), così come l’effetto di cambiamento proporzionale (\(\beta_x\)). Il modello di cambiamento duale produce una traiettoria di crescita esponenziale che dipende dal segno e dalla grandezza di \(g2_i\), \(\beta_x\) e \(lx1_i\) (si veda Grimm, An, McArdle, Zonderman e Resnick, 2012).
Per illustrare l’adattamento e l’interpretazione del modello di cambiamento duale, analizziamo i dati longitudinali di matematica che sono stati utilizzati nel Capitolo 3 di [GRE16]. I dati longitudinali di matematica sono stati raccolti dall’NLSY-CYA (Center for Human Resource Research, 2009) e i punteggi di matematica provengono dal PIAT (Dunn & Markwardt, 1970). Il grado scolastico al momento del test viene utilizzato come metrica temporale e varia dalla seconda elementare (grado 2) alla terza media (grado 8).
Importiamo i dati in R.
#set filepath
filepath <- "https://raw.githubusercontent.com/LRI-2/Data/main/GrowthModeling/nlsy_math_wide_R.dat"
#read in the text data file using the url() function
nlsy_data <- read.table(file=url(filepath),na.strings = ".")
#adding names for the columns of the data set
names(nlsy_data) <- c('id', 'female', 'lb_wght', 'anti_k1', 'math2', 'math3', 'math4', 'math5', 'math6', 'math7', 'math8', 'age2', 'age3', 'age4', 'age5', 'age6', 'age7', 'age8', 'men2', 'men3', 'men4', 'men5', 'men6', 'men7', 'men8', 'spring2', 'spring3', 'spring4', 'spring5', 'spring6', 'spring7', 'spring8', 'anti2', 'anti3', 'anti4', 'anti5', 'anti6', 'anti7', 'anti8')
#reduce data down to the id variable and the math and reading variables of interest
nlsy_uni_data <- nlsy_data[ ,c('id', 'math2', 'math3', 'math4', 'math5', 'math6', 'math7', 'math8')]
Otteniamo le statistiche descrittive.
psych::describe(nlsy_uni_data) |>
print()
vars n mean sd median trimmed mad min max
id 1 933 532334.90 328020.79 506602.0 520130.77 391999.44 201 1256601
math2 2 335 32.61 10.29 32.0 32.28 10.38 12 60
math3 3 431 39.88 10.30 41.0 39.88 10.38 13 67
math4 4 378 46.17 10.17 46.0 46.22 8.90 18 70
math5 5 372 49.77 9.47 48.0 49.77 8.90 23 71
math6 6 390 52.72 9.92 50.5 52.38 9.64 24 78
math7 7 173 55.35 10.63 53.0 55.09 11.86 31 81
math8 8 142 57.83 11.53 56.0 57.43 12.60 26 81
range skew kurtosis se
id 1256400 0.28 -0.91 10738.92
math2 48 0.27 -0.46 0.56
math3 54 -0.05 -0.33 0.50
math4 52 -0.06 -0.08 0.52
math5 48 0.04 -0.34 0.49
math6 54 0.25 -0.38 0.50
math7 50 0.21 -0.97 0.81
math8 55 0.16 -0.52 0.97
Selezioneremo dal data set solo le variabili ‘math2’, ‘math3’, ‘math4’, ‘math5’, ‘math6’,’math7’ e ‘math8’.
x_var_list <- paste0("math", 2:8)
x_var_list |>
print()
[1] "math2" "math3" "math4" "math5" "math6" "math7" "math8"
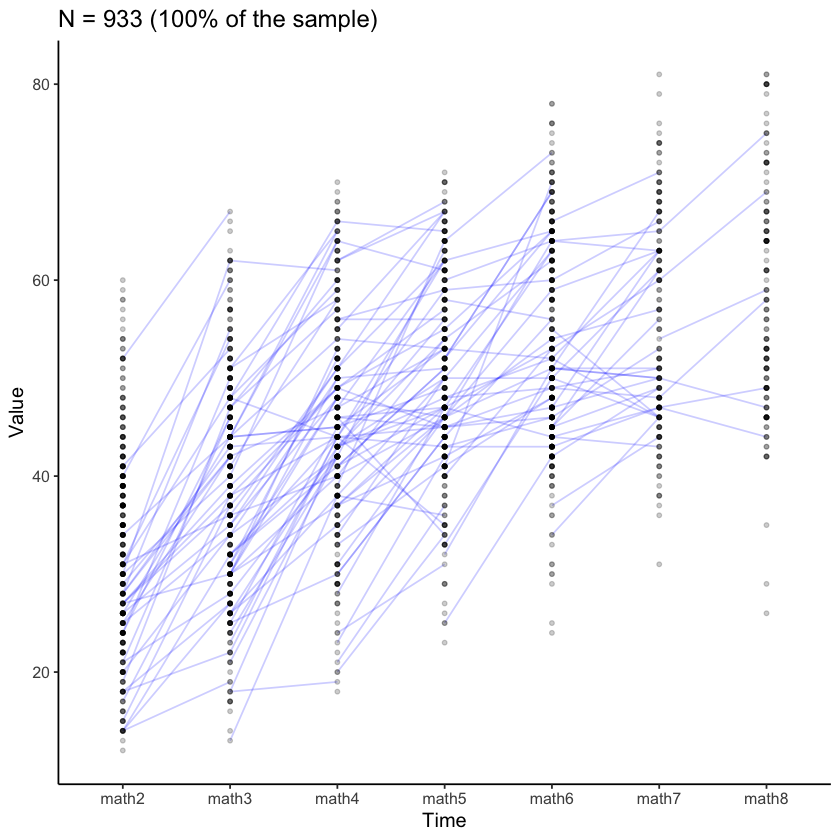
Esaminiamo le traiettorie di crescita nel campione.
plot_trajectories(
data = nlsy_uni_data,
id_var = "id",
var_list = x_var_list,
xlab = "Time", ylab = "Value",
connect_missing = FALSE,
# random_sample_frac = 0.018,
title_n = TRUE
)
Warning message:
“Removed 2787 rows containing missing values (`geom_line()`).”
Warning message:
“Removed 4310 rows containing missing values (`geom_point()`).”
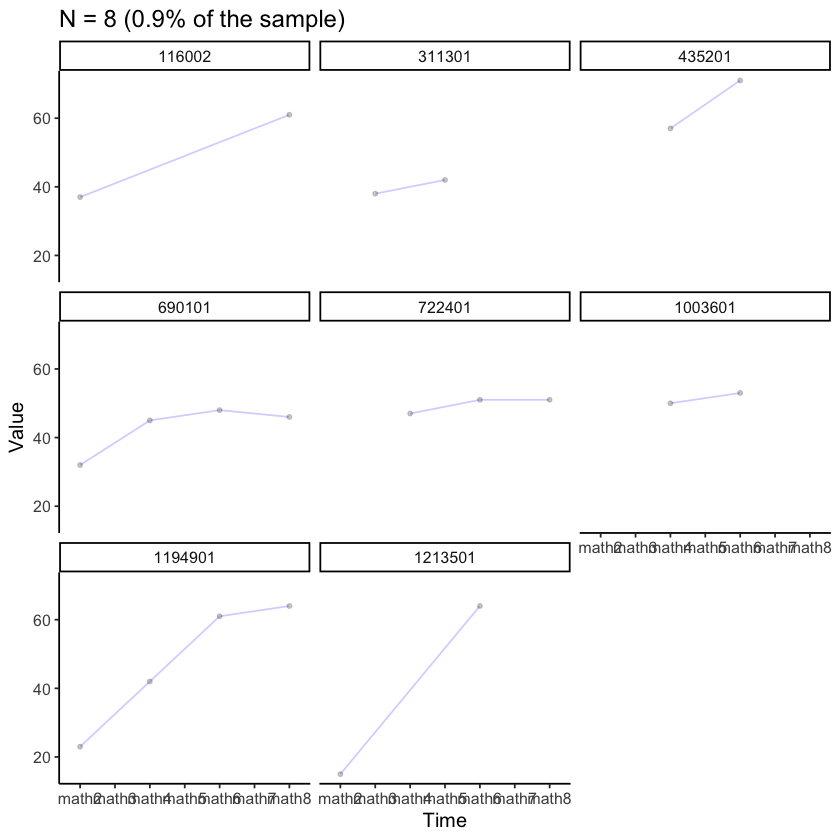
Esaminiamo i dati di alcuni soggetti presi a caso.
plot_trajectories(
data = nlsy_uni_data,
id_var = "id",
var_list = x_var_list,
xlab = "Time", ylab = "Value",
connect_missing = TRUE,
random_sample_frac = 0.009,
title_n = TRUE) +
facet_wrap(~id)
Warning message:
“Removed 35 rows containing missing values (`geom_point()`).”
uni_lavaan_results <- fit_uni_lcsm(
data = nlsy_uni_data,
var = x_var_list,
model = list(alpha_constant = TRUE,
beta = TRUE,
phi = TRUE)
)
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING: some cases are empty and will be ignored:
741”
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING:
due to missing values, some pairwise combinations have less than
10% coverage; use lavInspect(fit, "coverage") to investigate.”
Warning message in lav_mvnorm_missing_h1_estimate_moments(Y = X[[g]], wt = WT[[g]], :
“lavaan WARNING:
Maximum number of iterations reached when computing the sample
moments using EM; use the em.h1.iter.max= argument to increase the
number of iterations”
uni_lavaan_syntax <- fit_uni_lcsm(
data = nlsy_uni_data,
var = x_var_list,
model = list(
alpha_constant = TRUE,
beta = TRUE,
phi = TRUE
),
return_lavaan_syntax = TRUE
)
# Plot the results
plot_lcsm(
lavaan_object = uni_lavaan_results,
lavaan_syntax = uni_lavaan_syntax,
edge.label.cex = .9,
lcsm_colours = TRUE,
lcsm = "univariate"
)
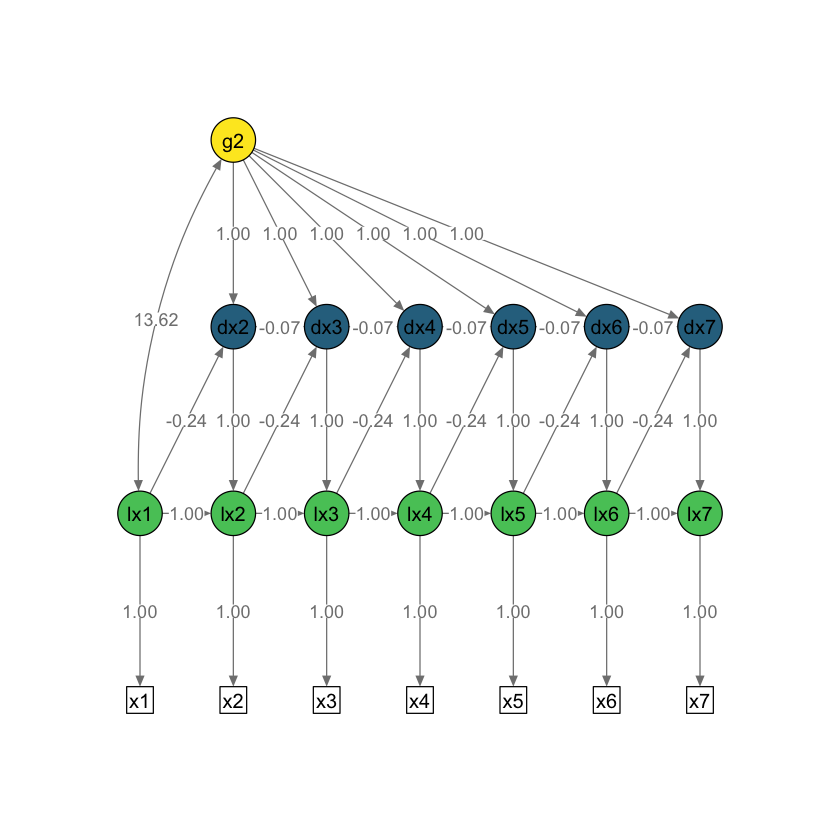
Esaminiamo la bontà di adattamento.
extract_fit(uni_lavaan_results) |>
print()
# A tibble: 1 × 8
model chisq npar aic bic cfi rmsea srmr
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 57.4 8 15806. 15845. 0.964 0.0347 0.138
Notiamo che le informazioni sull’adattamento del modello fornite da lcsm indicano che il modello di cambiamento duale si adatta bene ai dati con forti indici di adattamento globale (ad esempio, RMSEA inferiore a 0.05, CFI > 0.95).
extract_param(uni_lavaan_results) |>
print()
# A tibble: 8 × 8
label estimate std.error statistic p.value std.lv std.all std.nox
<chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 gamma_lx1 32.4 0.463 70.0 0 3.82 3.82 3.82
2 sigma2_lx1 72.0 6.19 11.6 0 1 1 1
3 sigma2_ux 30.8 1.76 17.5 0 30.8 0.299 0.299
4 alpha_g2 15.6 0.955 16.3 0 6.44 6.44 6.44
5 sigma2_g2 5.84 0.944 6.19 6.13e-10 1 1 1
6 sigma_g2lx1 13.6 1.68 8.09 6.66e-16 0.664 0.664 0.664
7 beta_x -0.242 0.0198 -12.2 0 -1.10 -1.10 -1.10
8 phi_x -0.0652 0.0612 -1.07 2.87e- 1 -0.0941 -0.0941 -0.0941
L’output completo è fornito qui di seguito.
summary(uni_lavaan_results) |>
print()
lavaan 0.6.15 ended normally after 55 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 23
Number of equality constraints 15
Used Total
Number of observations 932 933
Number of missing patterns 60
Model Test User Model:
Standard Scaled
Test Statistic 57.364 59.371
Degrees of freedom 27 27
P-value (Chi-square) 0.001 0.000
Scaling correction factor 0.966
Yuan-Bentler correction (Mplus variant)
Parameter Estimates:
Standard errors Sandwich
Information bread Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|)
lx1 =~
x1 1.000
lx2 =~
x2 1.000
lx3 =~
x3 1.000
lx4 =~
x4 1.000
lx5 =~
x5 1.000
lx6 =~
x6 1.000
lx7 =~
x7 1.000
dx2 =~
lx2 1.000
dx3 =~
lx3 1.000
dx4 =~
lx4 1.000
dx5 =~
lx5 1.000
dx6 =~
lx6 1.000
dx7 =~
lx7 1.000
g2 =~
dx2 1.000
dx3 1.000
dx4 1.000
dx5 1.000
dx6 1.000
dx7 1.000
Regressions:
Estimate Std.Err z-value P(>|z|)
lx2 ~
lx1 1.000
lx3 ~
lx2 1.000
lx4 ~
lx3 1.000
lx5 ~
lx4 1.000
lx6 ~
lx5 1.000
lx7 ~
lx6 1.000
dx2 ~
lx1 (bt_x) -0.242 0.020 -12.245 0.000
dx3 ~
lx2 (bt_x) -0.242 0.020 -12.245 0.000
dx4 ~
lx3 (bt_x) -0.242 0.020 -12.245 0.000
dx5 ~
lx4 (bt_x) -0.242 0.020 -12.245 0.000
dx6 ~
lx5 (bt_x) -0.242 0.020 -12.245 0.000
dx7 ~
lx6 (bt_x) -0.242 0.020 -12.245 0.000
dx3 ~
dx2 (ph_x) -0.065 0.061 -1.065 0.287
dx4 ~
dx3 (ph_x) -0.065 0.061 -1.065 0.287
dx5 ~
dx4 (ph_x) -0.065 0.061 -1.065 0.287
dx6 ~
dx5 (ph_x) -0.065 0.061 -1.065 0.287
dx7 ~
dx6 (ph_x) -0.065 0.061 -1.065 0.287
Covariances:
Estimate Std.Err z-value P(>|z|)
lx1 ~~
g2 (s_21) 13.621 1.683 8.093 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
lx1 (gm_1) 32.378 0.463 69.999 0.000
.lx2 0.000
.lx3 0.000
.lx4 0.000
.lx5 0.000
.lx6 0.000
.lx7 0.000
.x1 0.000
.x2 0.000
.x3 0.000
.x4 0.000
.x5 0.000
.x6 0.000
.x7 0.000
.dx2 0.000
.dx3 0.000
.dx4 0.000
.dx5 0.000
.dx6 0.000
.dx7 0.000
g2 (al_2) 15.565 0.955 16.305 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
lx1 (s2_1) 72.010 6.185 11.642 0.000
.lx2 0.000
.lx3 0.000
.lx4 0.000
.lx5 0.000
.lx6 0.000
.lx7 0.000
.x1 (sg2_) 30.778 1.762 17.463 0.000
.x2 (sg2_) 30.778 1.762 17.463 0.000
.x3 (sg2_) 30.778 1.762 17.463 0.000
.x4 (sg2_) 30.778 1.762 17.463 0.000
.x5 (sg2_) 30.778 1.762 17.463 0.000
.x6 (sg2_) 30.778 1.762 17.463 0.000
.x7 (sg2_) 30.778 1.762 17.463 0.000
.dx2 0.000
.dx3 0.000
.dx4 0.000
.dx5 0.000
.dx6 0.000
.dx7 0.000
g2 (s2_2) 5.840 0.944 6.187 0.000
I parametri stimati del modello di cambiamento duale includono la media del punteggio vero iniziale, gamma_lx1. Il valore 32.38 del punteggio vero iniziale rappresenta la media predetta dei punteggi di matematica al grado 2. La media della componente di cambiamento costante è 15.56 ed è una delle componenti dei cambiamenti previsti nel tempo, con la seconda proveniente dall’effetto di cambiamento proporzionale. Poiché ci sono due aspetti del cambiamento nel modello di cambiamento duale, la media della componente di cambiamento costante può essere difficile da interpretare. Inoltre, la componente di cambiamento costante funziona come un’intercetta nell’equazione di cambiamento, il che rende il suo valore dipendente dalla scala della variabile osservata (cioè, aggiungendo o sottraendo una costante a tutti i punteggi altera la media della componente di cambiamento costante). E poiché la componente di cambiamento costante è un’intercetta nell’equazione di cambiamento, è interpretabile solo quando tutti gli altri predittori (punteggi veri precedenti) sono zero. Nei nostri dati, i punteggi di matematica non sono mai zero in questo set di dati, il che rende la media della componente di cambiamento costante un’estrapolazione dai dati e successivamente difficile da interpretare isolatamente.
A causa di queste limitazioni, descriviamo la forma complessiva dello sviluppo esaminando insieme la media della componente di cambiamento costante e il parametro di cambiamento proporzionale insieme alla media del punteggio vero iniziale. La traiettoria media inizia a 32.38 e aumenta in base a due aspetti: un effetto maturativo di 15.56 (media della componente di cambiamento costante), che viene aggiunto ad ogni grado, e l’effetto di cambiamento proporzionale, che funge da fattore limitante perché il parametro di cambiamento proporzionale è negativo (-0.24). Quindi, man mano che i punteggi aumentano nel tempo, aumentano a un ritmo più lento perché l’effetto di cambiamento proporzionale si rafforza nel tempo (perché i punteggi aumentano nel tempo). Per illustrare, abbiamo calcolato i cambiamenti medi previsti per i gradi successivi. Il cambiamento medio dalla seconda alla terza elementare è pari a 7.79 (\(15.56 -0.24 \cdot 32.38\)), il cambiamento medio dalla terza alla quarta elementare era 5.97 (\(15.56 -0.24 \cdot 39.94\)) e questo schema continua nel tempo. Quindi, la traiettoria media è una curva esponenziale crescente con un tasso di cambiamento decrescente.
Poniamoci dunque il problema di creare una figura che riporta le traiettorie individuali previste dal modello duale. Per creare la figura dobbiamo innanzitutto recuperare la sintassi lavaan del modello duale.
cat(uni_lavaan_syntax) |>
print()
# Specify latent true scores
lx1 =~ 1 * x1
lx2 =~ 1 * x2
lx3 =~ 1 * x3
lx4 =~ 1 * x4
lx5 =~ 1 * x5
lx6 =~ 1 * x6
lx7 =~ 1 * x7
# Specify mean of latent true scores
lx1 ~ gamma_lx1 * 1
lx2 ~ 0 * 1
lx3 ~ 0 * 1
lx4 ~ 0 * 1
lx5 ~ 0 * 1
lx6 ~ 0 * 1
lx7 ~ 0 * 1
# Specify variance of latent true scores
lx1 ~~ sigma2_lx1 * lx1
lx2 ~~ 0 * lx2
lx3 ~~ 0 * lx3
lx4 ~~ 0 * lx4
lx5 ~~ 0 * lx5
lx6 ~~ 0 * lx6
lx7 ~~ 0 * lx7
# Specify intercept of obseved scores
x1 ~ 0 * 1
x2 ~ 0 * 1
x3 ~ 0 * 1
x4 ~ 0 * 1
x5 ~ 0 * 1
x6 ~ 0 * 1
x7 ~ 0 * 1
# Specify variance of observed scores
x1 ~~ sigma2_ux * x1
x2 ~~ sigma2_ux * x2
x3 ~~ sigma2_ux * x3
x4 ~~ sigma2_ux * x4
x5 ~~ sigma2_ux * x5
x6 ~~ sigma2_ux * x6
x7 ~~ sigma2_ux * x7
# Specify autoregressions of latent variables
lx2 ~ 1 * lx1
lx3 ~ 1 * lx2
lx4 ~ 1 * lx3
lx5 ~ 1 * lx4
lx6 ~ 1 * lx5
lx7 ~ 1 * lx6
# Specify latent change scores
dx2 =~ 1 * lx2
dx3 =~ 1 * lx3
dx4 =~ 1 * lx4
dx5 =~ 1 * lx5
dx6 =~ 1 * lx6
dx7 =~ 1 * lx7
# Specify latent change scores means
dx2 ~ 0 * 1
dx3 ~ 0 * 1
dx4 ~ 0 * 1
dx5 ~ 0 * 1
dx6 ~ 0 * 1
dx7 ~ 0 * 1
# Specify latent change scores variances
dx2 ~~ 0 * dx2
dx3 ~~ 0 * dx3
dx4 ~~ 0 * dx4
dx5 ~~ 0 * dx5
dx6 ~~ 0 * dx6
dx7 ~~ 0 * dx7
# Specify constant change factor
g2 =~ 1 * dx2 + 1 * dx3 + 1 * dx4 + 1 * dx5 + 1 * dx6 + 1 * dx7
# Specify constant change factor mean
g2 ~ alpha_g2 * 1
# Specify constant change factor variance
g2 ~~ sigma2_g2 * g2
# Specify constant change factor covariance with the initial true score
g2 ~~ sigma_g2lx1 * lx1
# Specify proportional change component
dx2 ~ beta_x * lx1
dx3 ~ beta_x * lx2
dx4 ~ beta_x * lx3
dx5 ~ beta_x * lx4
dx6 ~ beta_x * lx5
dx7 ~ beta_x * lx6
# Specify autoregression of change score
dx3 ~ phi_x * dx2
dx4 ~ phi_x * dx3
dx5 ~ phi_x * dx4
dx6 ~ phi_x * dx5
dx7 ~ phi_x * dx6
NULL
Creaimo un oggetto mod che contiene la specificazione del modello duale con la sintassi di lavaan.
mod = '
# Specify latent true scores
lx1 =~ 1 * x1
lx2 =~ 1 * x2
lx3 =~ 1 * x3
lx4 =~ 1 * x4
lx5 =~ 1 * x5
lx6 =~ 1 * x6
lx7 =~ 1 * x7
# Specify mean of latent true scores
lx1 ~ gamma_lx1 * 1
lx2 ~ 0 * 1
lx3 ~ 0 * 1
lx4 ~ 0 * 1
lx5 ~ 0 * 1
lx6 ~ 0 * 1
lx7 ~ 0 * 1
# Specify variance of latent true scores
lx1 ~~ sigma2_lx1 * lx1
lx2 ~~ 0 * lx2
lx3 ~~ 0 * lx3
lx4 ~~ 0 * lx4
lx5 ~~ 0 * lx5
lx6 ~~ 0 * lx6
lx7 ~~ 0 * lx7
# Specify intercept of obseved scores
x1 ~ 0 * 1
x2 ~ 0 * 1
x3 ~ 0 * 1
x4 ~ 0 * 1
x5 ~ 0 * 1
x6 ~ 0 * 1
x7 ~ 0 * 1
# Specify variance of observed scores
x1 ~~ sigma2_ux * x1
x2 ~~ sigma2_ux * x2
x3 ~~ sigma2_ux * x3
x4 ~~ sigma2_ux * x4
x5 ~~ sigma2_ux * x5
x6 ~~ sigma2_ux * x6
x7 ~~ sigma2_ux * x7
# Specify autoregressions of latent variables
lx2 ~ 1 * lx1
lx3 ~ 1 * lx2
lx4 ~ 1 * lx3
lx5 ~ 1 * lx4
lx6 ~ 1 * lx5
lx7 ~ 1 * lx6
# Specify latent change scores
dx2 =~ 1 * lx2
dx3 =~ 1 * lx3
dx4 =~ 1 * lx4
dx5 =~ 1 * lx5
dx6 =~ 1 * lx6
dx7 =~ 1 * lx7
# Specify latent change scores means
dx2 ~ 0 * 1
dx3 ~ 0 * 1
dx4 ~ 0 * 1
dx5 ~ 0 * 1
dx6 ~ 0 * 1
dx7 ~ 0 * 1
# Specify latent change scores variances
dx2 ~~ 0 * dx2
dx3 ~~ 0 * dx3
dx4 ~~ 0 * dx4
dx5 ~~ 0 * dx5
dx6 ~~ 0 * dx6
dx7 ~~ 0 * dx7
# Specify constant change factor
g2 =~ 1 * dx2 + 1 * dx3 + 1 * dx4 + 1 * dx5 + 1 * dx6 + 1 * dx7
# Specify constant change factor mean
g2 ~ alpha_g2 * 1
# Specify constant change factor variance
g2 ~~ sigma2_g2 * g2
# Specify constant change factor covariance with the initial true score
g2 ~~ sigma_g2lx1 * lx1
# Specify proportional change component
dx2 ~ beta_x * lx1
dx3 ~ beta_x * lx2
dx4 ~ beta_x * lx3
dx5 ~ beta_x * lx4
dx6 ~ beta_x * lx5
dx7 ~ beta_x * lx6
# Specify autoregression of change score
dx3 ~ phi_x * dx2
dx4 ~ phi_x * dx3
dx5 ~ phi_x * dx4
dx6 ~ phi_x * dx5
dx7 ~ phi_x * dx6
'
Dato che nella specificazione del modello le variabili osservate sono chiamate x1, …, x8, dobbiamo trasformare il file dei dati in maniera corrispondente.
new_var_names <- c("id", paste0("x", 1:7))
new_var_names |>
print()
[1] "id" "x1" "x2" "x3" "x4" "x5" "x6" "x7"
newdat <- nlsy_uni_data
names(newdat) <- new_var_names
head(newdat)
| id | x1 | x2 | x3 | x4 | x5 | x6 | x7 | |
|---|---|---|---|---|---|---|---|---|
| <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | |
| 1 | 201 | NA | 38 | NA | 55 | NA | NA | NA |
| 2 | 303 | 26 | NA | NA | 33 | NA | NA | NA |
| 3 | 2702 | 56 | NA | 58 | NA | NA | NA | 80 |
| 4 | 4303 | NA | 41 | 58 | NA | NA | NA | NA |
| 5 | 5002 | NA | NA | 46 | NA | 54 | NA | 66 |
| 6 | 5005 | 35 | NA | 50 | NA | 60 | NA | 59 |
Adattiamo ora il modello duale ai dati usando sem.
fit = sem(mod, newdat, missing="fiml")
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING: some cases are empty and will be ignored:
741”
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING:
due to missing values, some pairwise combinations have less than
10% coverage; use lavInspect(fit, "coverage") to investigate.”
Warning message in lav_mvnorm_missing_h1_estimate_moments(Y = X[[g]], wt = WT[[g]], :
“lavaan WARNING:
Maximum number of iterations reached when computing the sample
moments using EM; use the em.h1.iter.max= argument to increase the
number of iterations”
L’output che abbiamo ottenuto è identico a quello trovato in precedenza.
summary(fit) |>
print()
lavaan 0.6.15 ended normally after 55 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 23
Number of equality constraints 15
Used Total
Number of observations 932 933
Number of missing patterns 60
Model Test User Model:
Test statistic 57.364
Degrees of freedom 27
P-value (Chi-square) 0.001
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|)
lx1 =~
x1 1.000
lx2 =~
x2 1.000
lx3 =~
x3 1.000
lx4 =~
x4 1.000
lx5 =~
x5 1.000
lx6 =~
x6 1.000
lx7 =~
x7 1.000
dx2 =~
lx2 1.000
dx3 =~
lx3 1.000
dx4 =~
lx4 1.000
dx5 =~
lx5 1.000
dx6 =~
lx6 1.000
dx7 =~
lx7 1.000
g2 =~
dx2 1.000
dx3 1.000
dx4 1.000
dx5 1.000
dx6 1.000
dx7 1.000
Regressions:
Estimate Std.Err z-value P(>|z|)
lx2 ~
lx1 1.000
lx3 ~
lx2 1.000
lx4 ~
lx3 1.000
lx5 ~
lx4 1.000
lx6 ~
lx5 1.000
lx7 ~
lx6 1.000
dx2 ~
lx1 (bt_x) -0.242 0.019 -12.869 0.000
dx3 ~
lx2 (bt_x) -0.242 0.019 -12.869 0.000
dx4 ~
lx3 (bt_x) -0.242 0.019 -12.869 0.000
dx5 ~
lx4 (bt_x) -0.242 0.019 -12.869 0.000
dx6 ~
lx5 (bt_x) -0.242 0.019 -12.869 0.000
dx7 ~
lx6 (bt_x) -0.242 0.019 -12.869 0.000
dx3 ~
dx2 (ph_x) -0.065 0.067 -0.978 0.328
dx4 ~
dx3 (ph_x) -0.065 0.067 -0.978 0.328
dx5 ~
dx4 (ph_x) -0.065 0.067 -0.978 0.328
dx6 ~
dx5 (ph_x) -0.065 0.067 -0.978 0.328
dx7 ~
dx6 (ph_x) -0.065 0.067 -0.978 0.328
Covariances:
Estimate Std.Err z-value P(>|z|)
lx1 ~~
g2 (s_21) 13.621 1.772 7.688 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
lx1 (gm_1) 32.378 0.463 69.888 0.000
.lx2 0.000
.lx3 0.000
.lx4 0.000
.lx5 0.000
.lx6 0.000
.lx7 0.000
.x1 0.000
.x2 0.000
.x3 0.000
.x4 0.000
.x5 0.000
.x6 0.000
.x7 0.000
.dx2 0.000
.dx3 0.000
.dx4 0.000
.dx5 0.000
.dx6 0.000
.dx7 0.000
g2 (al_2) 15.565 0.916 16.995 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
lx1 (s2_1) 72.010 6.599 10.912 0.000
.lx2 0.000
.lx3 0.000
.lx4 0.000
.lx5 0.000
.lx6 0.000
.lx7 0.000
.x1 (sg2_) 30.778 1.691 18.196 0.000
.x2 (sg2_) 30.778 1.691 18.196 0.000
.x3 (sg2_) 30.778 1.691 18.196 0.000
.x4 (sg2_) 30.778 1.691 18.196 0.000
.x5 (sg2_) 30.778 1.691 18.196 0.000
.x6 (sg2_) 30.778 1.691 18.196 0.000
.x7 (sg2_) 30.778 1.691 18.196 0.000
.dx2 0.000
.dx3 0.000
.dx4 0.000
.dx5 0.000
.dx6 0.000
.dx7 0.000
g2 (s2_2) 5.840 0.925 6.313 0.000
Calcoliamo ora i punteggi fattoriali.
fs = lavPredict(fit)
head(fs) |>
print()
lx1 lx2 lx3 lx4 lx5 lx6 lx7 dx2
[1,] 32.91853 41.15381 46.85997 51.35058 54.83407 57.54049 59.64284 8.235283
[2,] 24.11723 30.82850 35.47868 39.13826 41.97710 44.18267 45.89596 6.711269
[3,] 49.15305 57.02307 62.47613 66.76757 70.09655 72.68293 74.69203 7.870019
[4,] 37.18693 45.42767 51.13761 55.63120 59.11699 61.82521 63.92895 8.240744
[5,] 33.65976 42.09359 47.93732 52.53619 56.10366 58.87533 61.02836 8.433826
[6,] 35.57593 43.49181 48.97665 53.29308 56.64146 59.24292 61.26373 7.915874
dx3 dx4 dx5 dx6 dx7 g2
[1,] 5.706156 4.490607 3.483489 2.706424 2.102348 16.19888
[2,] 4.650180 3.659579 2.838838 2.205576 1.713289 12.54567
[3,] 5.453067 4.291433 3.328984 2.586384 2.009101 19.76104
[4,] 5.709939 4.493585 3.485799 2.708219 2.103742 17.23694
[5,] 5.843724 4.598870 3.567472 2.771673 2.153033 16.57674
[6,] 5.484840 4.316437 3.348381 2.601454 2.020807 16.52234
Consideriamo le stime dei punteggi veri nelle 7 rilevazioni temporali.
lx_fs = fs[, 1:7]
head(lx_fs) |>
print()
lx1 lx2 lx3 lx4 lx5 lx6 lx7
[1,] 32.91853 41.15381 46.85997 51.35058 54.83407 57.54049 59.64284
[2,] 24.11723 30.82850 35.47868 39.13826 41.97710 44.18267 45.89596
[3,] 49.15305 57.02307 62.47613 66.76757 70.09655 72.68293 74.69203
[4,] 37.18693 45.42767 51.13761 55.63120 59.11699 61.82521 63.92895
[5,] 33.65976 42.09359 47.93732 52.53619 56.10366 58.87533 61.02836
[6,] 35.57593 43.49181 48.97665 53.29308 56.64146 59.24292 61.26373
dim(lx_fs)
- 933
- 7
dd <- as_tibble(lx_fs)
dim(dd)
- 933
- 7
Aggiungiamo la variabile id.
dd$id <- 1:933
head(dd) |>
print()
# A tibble: 6 × 8
lx1 lx2 lx3 lx4 lx5 lx6 lx7 id
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <int>
1 32.9 41.2 46.9 51.4 54.8 57.5 59.6 1
2 24.1 30.8 35.5 39.1 42.0 44.2 45.9 2
3 49.2 57.0 62.5 66.8 70.1 72.7 74.7 3
4 37.2 45.4 51.1 55.6 59.1 61.8 63.9 4
5 33.7 42.1 47.9 52.5 56.1 58.9 61.0 5
6 35.6 43.5 49.0 53.3 56.6 59.2 61.3 6
Creiamo un vettore con i nuovi nomi delle variabili.
vlist = paste0("lx", 1:7)
vlist |>
print()
[1] "lx1" "lx2" "lx3" "lx4" "lx5" "lx6" "lx7"
Le traiettorie di sviluppo individuale previste dal modello duale si possono ora visualizzare usando plot_trajectories.
plot_trajectories(
data = dd,
id_var = "id",
var_list = vlist,
xlab = "Time", ylab = "Value",
connect_missing = FALSE,
# random_sample_frac = 0.018,
title_n = TRUE
)
Warning message:
“Removed 7 rows containing missing values (`geom_line()`).”
Warning message:
“Removed 7 rows containing missing values (`geom_point()`).”
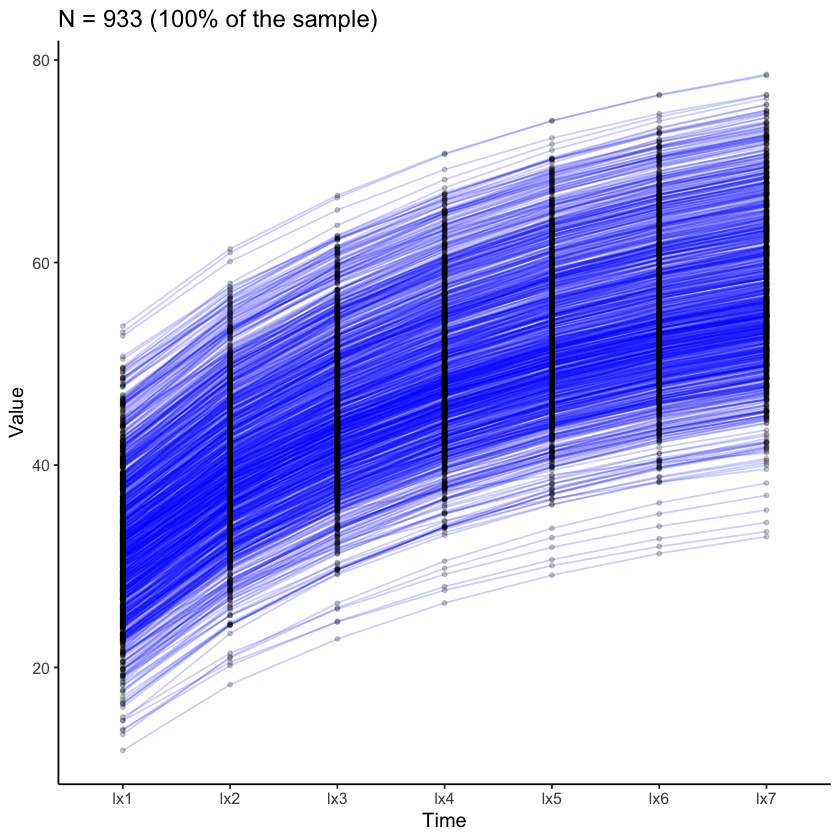
Come si vede dalla figura, tutte le traiettorie previste mostrano la forma generale di crescita che era stata descritta in precedenza.
La varianza del punteggio vero iniziale è 72.01 e descrive la variabilità inter-personale dei punteggi veri di matematica per il grado 2 (seconda elementare).
La varianza della componente di cambiamento costante è 5.84 e rappresenta la variabilità tra i bambini in questo aspetto del cambiamento (di nuovo i parametri associati alla componente di cambiamento costante sono difficili da interpretare isolatamente).
La covarianza tra il punteggio vero iniziale e la componente di cambiamento costante era 13.62, indicando che i bambini con punteggi veri di matematica più alti al grado 2 tendevano ad avere punteggi nella componente di cambiamento costante più elevati, il che rivela un cambiamento complessivo maggiore dal secondo all’ottavo grado.
Infine, la varianza dei punteggi unici era 30.78 e indica l’entità delle fluttuazioni intra-personali attorno alle traiettorie individuali predette dal modello.
