28. Curve di crescita latente

Quando si vuole studiare le differenze tra le persone, si confrontano i loro punteggi. Ma se l’attenzione è invece sui cambiamenti all’interno di ciascuna persona, sono necessarie informazioni longitudinali, cioè raccolte nel tempo, per descrivere le traiettorie di cambiamento. Per fare questo, occorre utilizzare un modello statistico che tenga conto sia delle differenze tra le persone sia dei cambiamenti nel tempo all’interno di ciascuna persona. Ci sono due approcci statistici principali per affrontare questo problema: i modelli misti e un’estensione del framework SEM (Structural Equation Modeling) per dati longitudinali. Nel resto del testo, si fornirà una panoramica su questi approcci, concentrandosi in particolare sul framework SEM per dati longitudinali.

28.1. Misurare il cambiamento

Il modo più semplice per valutare il cambiamento individuale tra due momenti temporali è calcolare la differenza tra i punteggi ottenuti nelle due occasioni. Tuttavia, questa strategia presenta un problema: non conosciamo il vero punteggio dell’individuo nei due momenti temporali, ma solo un punteggio influenzato dall’errore di misurazione. L’errore di misura può ridurre drasticamente la precisione delle valutazioni sulle differenze individuali nel cambiamento.

Per affrontare il problema dell’analisi di dati longitudinali, sono stati introdotti modelli SEM chiamati Latent Growth Models (LGM). Questi modelli assumono che ogni individuo abbia una traiettoria di cambiamento latente unica nel tempo. Quindi, i dati raccolti in ogni momento temporale sono considerati come la somma di tre componenti: (a) punteggi latenti o non osservati che rappresentano il livello dell’individuo in quel momento, (b) punteggi latenti che rappresentano il cambiamento individuale nel tempo, e (c) caratteristiche uniche e non osservate ma indipendenti delle misurazioni.

Questa formulazione del modello SEM per dati longitudinali prevede tre fattori latenti:

• un fattore latente comune che rappresenta il livello latente dell’individuo in un momento temporale specifico (rappresentato dal punto a);

• un fattore latente comune che rappresenta il cambiamento latente del livello dell’individuo tra due momenti temporali consecutivi (rappresentato dal punto b);

• un fattore latente specifico che rappresenta l’errore di misurazione in ogni momento temporale \(t\) (rappresentato dal punto c).

In questo modo, i dati osservati in ogni momento temporale sono considerati come la somma dei tre fattori latenti. Il punteggio osservato della persona \(i\) al tempo \(t\) può essere espresso come:

\[ x_{it} = \tau_i + (1)\xi_1 + (t)\xi_2 + \delta_{it} \]

dove \(\tau_i\) rappresenta il livello latente dell’individuo \(i\) al tempo iniziale, \(\xi_1\) rappresenta il carico del fattore comune per il livello latente, \(\xi_2\) rappresenta il carico del fattore comune per il cambiamento latente e \(\delta_{it}\) rappresenta l’errore di misura specifico del momento \(t\) per l’individuo \(i\).

Nel modello, le intercette osservate sono vincolate ad essere 0, per cui \(\tau_i = 0\). In un modello LGM, l’intercetta osservata è fissata a zero poiché si assume che il livello iniziale di ogni individuo sia rappresentato dal fattore latente comune nel momento \(t_1\), e quindi il valore osservato della variabile dipendente al tempo \(t_1\) sarà uguale al valore latente di quel fattore comune. Inoltre, fissare l’intercetta osservata a zero semplifica il modello e ne facilita l’interpretazione, poiché la variazione nella variabile dipendente può essere attribuita solo ai fattori latenti di cambiamento.

Se ci sono cinque misurazioni temporali, per esempio, il modello diventa

\[\begin{split} \begin{align} x_{1} &= 0 + (1)\xi_{1} + (0)\xi_{2} + \delta_{1} \notag\\ x_{2} &= 0 + (1)\xi_{1} + (1)\xi_{2} + \delta_{2} \notag\\ x_{3} &= 0 + (1)\xi_{1} + (2)\xi_{2} + \delta_{3} \notag\\ x_{4} &= 0 + (1)\xi_{1} + (3)\xi_{2} + \delta_{4} \notag\\ x_{5} &= 0 + (1)\xi_{1} + (4)\xi_{2} + \delta_{5} \notag \end{align} \end{split}\]

Inoltre, il modello ipotizza che \(\xi_1\) e \(\xi_e\) siano correlati, come indicato nella matrice di inter-correlazione fattoriale

\[\begin{split} \mathbf{\Phi} = \begin{bmatrix} \phi_{11} & \\ \phi_{21} & \phi_{22} \end{bmatrix} \end{split}\]

dove \(\phi_{11}\) è la varianza dell’intercetta latente, \(\phi_{22}\) è la varianza della pendenza latente e \(\phi_{21}\) è la covarianza dell’intercetta e della pendenza.

La figura Modello di crescita latente mostra il diagramma di percorso che rappresenta il modello LGM che stiamo discutendo:

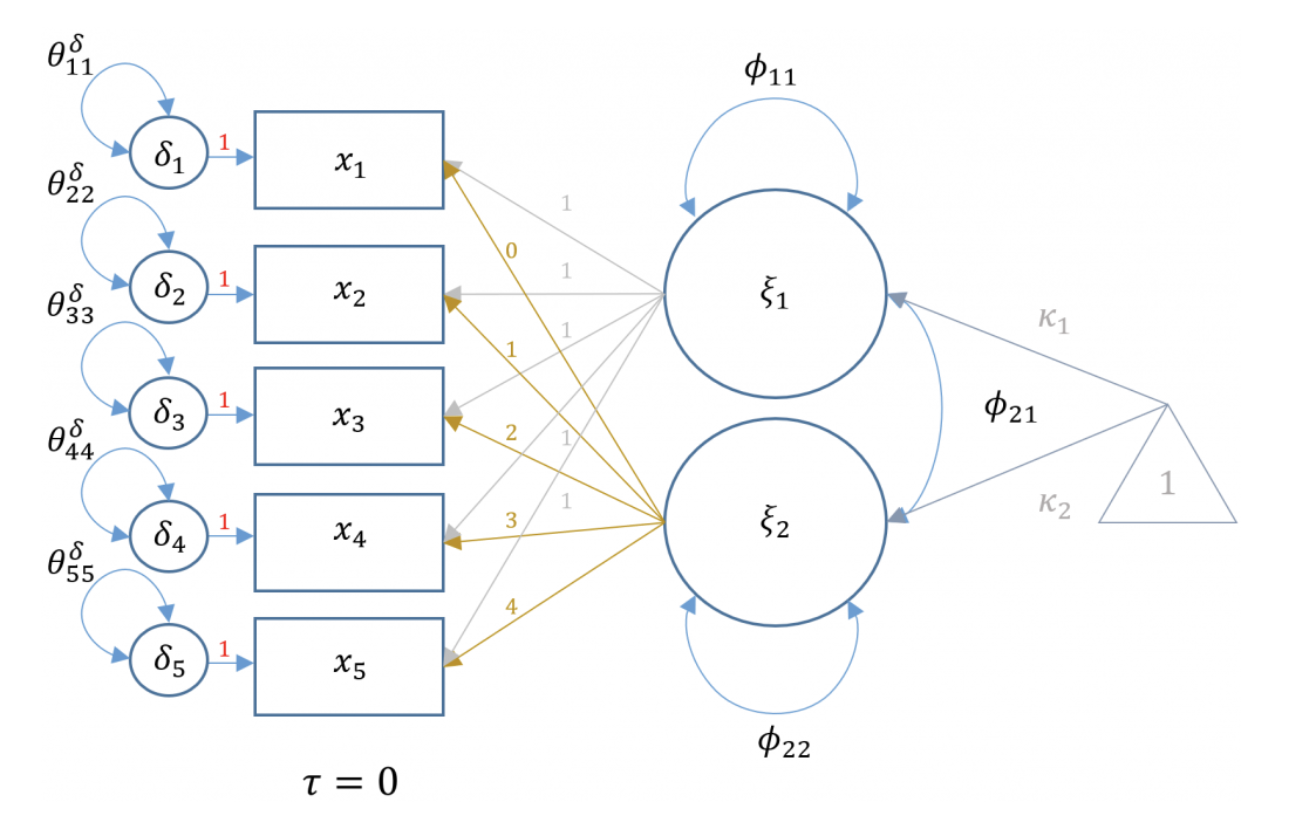
Fig. 28.1 Modello di crescita latente

Il modello di crescita latente definito dalle equazioni precedenti porta a una serie di previsioni sulla struttura delle medie e delle covarianze dei dati osservati. Queste previsioni del modello vengono utilizzate nel contesto della modellizzazione delle equazioni strutturali per calcolare le stime dei parametri e gli indici di adattamento del modello. La struttura delle covarianze (\(\boldsymbol{\Sigma}\)) prevista dal modello di crescita latente è

\[ \boldsymbol{\Sigma} = \boldsymbol{\Lambda} \boldsymbol{\Phi} \boldsymbol{\Lambda}' + \boldsymbol{\Theta}. \]

Diversi tipi di modelli di crescita latente possono essere specificati cambiando le dimensioni e i valori contenuti nella matrice \(\boldsymbol{Λ}\). Per il modello senza crescita, \(\boldsymbol{Λ}\) è una matrice T × 1 (colonna) perché c’è solo una variabile latente nel modello senza crescita. Per il modello a crescita lineare, \(\boldsymbol{Λ}\) è una matrice T × k, con k rilevazioni temporali, dove le saturazioni fattoriali sono fisse e uguali alla separazione temporale tra le rilevazioni. Per esempio, con cinque misurazioni temporali, le saturazioni fattoriali saranno specificate ai valori 0, 1, 2, 3, 4. Si noti che, in questo modo, si assume che tutte le unità di osservazione siano state misurate nella stessa occasione temporale. A differenza dei modelli CFA tradizionali in cui l’interpretazione si concentra sulle saturazioni fattoriali, nei modelli di crescita latente le saturazioni fattoriali sono fisse

\[\begin{split} \Lambda = \begin{pmatrix} 1 & 0 \\ 1 & 1 \\ 1 & 2 \\ 1 & 3 \\ 1 & 4 \\ \end{pmatrix} \end{split}\]

il che implica che l’attenzione è rivolta all’intercetta latente e al fattore di pendenza latente.

Il modello LGC è un modello che ci permette di osservare la media e la varianza dei punteggi iniziali e del tasso di crescita dei partecipanti nel tempo. Ci aiuta a rispondere a domande classiche sulla crescita e lo sviluppo, come “Quanto cambiano gli studenti nel tempo?”, “Quanto varia la velocità di crescita?” e “Quanto differiscono gli studenti inizialmente?”. Il modello può essere reso più complesso per adattarsi a situazioni diverse, ma l’idea di base è di avere una media di crescita comune per tutti i partecipanti e poi considerare le differenze individuali nel tasso di crescita. Nella versione più semplice del modello, la pendenza della curva di crescita viene fatta coincidere con una crescita lineare, ma è possibile ampliare il modello includendo anche una crescita quadratico o altre forme di crescita. Inoltre, è possibile stimare i parametri del modello in modo da rendere più flessibile il modello per adattarsi a diverse situazioni di crescita.

28.2. Domande della ricerca

L’analisi di dati longitudinali nella ricerca psicologica è particolarmente interessata a valutare quanto le persone cambino in un particolare aspetto o tratto nel tempo (cioè la crescita media), quanto questa crescita varia rispetto agli altri individui (cioè la varianza della crescita), e come le persone cambiano rispetto a se stesse nel tempo (cioè i modelli di crescita intra-individuale). I modelli di crescita media (LGM) descrivono i primi due di questi elementi chiave, mentre i modelli di punteggio di cambiamento latente (LCSM) descrivono il terzo (come i valori precedenti prevedono i valori successivi nel tempo all’interno della stessa persona).

In ambito di ricerca psicologica, l’analisi di dati longitudinali si concentra sullo studio di come le persone cambiano in un particolare tratto o aspetto nel tempo, sulla variazione di questo cambiamento rispetto ad altre persone e su come le persone cambiano rispetto a se stesse nel tempo. I modelli di crescita media (LGM) e quelli di punteggio di cambiamento latente (LCSM) vengono utilizzati per descrivere questi aspetti.

Grimm et al. [GRE16] identificano cinque motivi principali per cui questi modelli vengono utilizzati. In primo luogo, l’analisi longitudinale consente di identificare direttamente il cambiamento e la stabilità intra-individuale. Ciò significa che è possibile valutare in che modo specifici attributi dell’individuo cambiano o rimangono gli stessi nel tempo, attraverso la misurazione ripetuta della stessa persona.

In secondo luogo, l’analisi longitudinale consente di identificare le differenze interindividuali nel cambiamento intra-individuale, ovvero se diversi individui cambiano in modi diversi, in quantità o direzioni diverse o se passano da uno stadio all’altro in momenti diversi.

In terzo luogo, l’analisi longitudinale consente di analizzare le interrelazioni nel cambiamento comportamentale, ovvero come i cambiamenti in una variabile influenzino i cambiamenti in un’altra variabile.

In quarto luogo, l’analisi longitudinale consente di analizzare le cause del cambiamento intra-individuale, ovvero di identificare i fattori e/o i meccanismi variabili nel tempo che influenzano i cambiamenti intra-individuali.

Infine, in quinto luogo, l’analisi longitudinale consente di analizzare le cause delle differenze interindividuali nel cambiamento intra-individuale, ovvero di identificare le variabili invarianti nel tempo che sono correlate a specifici aspetti del cambiamento all’interno della persona, come le caratteristiche demografiche, gli interventi sperimentali e le caratteristiche dei contesti degli individui.