8. Il modello unifattoriale#
Questo capitolo presenta le nozioni fondamentali dell’analisi fattoriale, un modello statistico che consente di spiegare le correlazioni tra variabili osservate mediante la loro saturazione in uno o più fattori generali. In questo modello, le \(p\) variabili osservate (item) sono considerate condizionalmente indipendenti rispetto a \(m\) variabili latenti chiamate fattori. L’obiettivo dell’analisi fattoriale è di interpretare questi fattori come costrutti teorici inosservabili. Ad esempio, l’analisi fattoriale può essere utilizzata per spiegare le correlazioni tra le prestazioni di un gruppo di individui in una serie di compiti mediante il concetto di intelligenza. In questo modo, l’analisi fattoriale aiuta a identificare i costrutti cui gli item si riferiscono e a stabilire in che misura ciascun item rappresenta il costrutto. Il modello può essere unifattoriale (\(m = 1\)) o multifattoriale (\(m > 1\)), e in questo capitolo si introdurrà il modello unifattoriale che assume l’esistenza di un unico fattore comune latente.
8.1. Errore di misura#
L’analisi fattoriale modella ogni misura osservata \(y\) come una combinazione del punteggio vero del costrutto latente \(\xi\) e di una componente di errore di misura latente \(\delta\). In altre parole, il valore osservato di \(y\) è dato dalla somma del punteggio vero latente moltiplicato per il carico fattoriale \(\lambda\) e di un errore di misura latente \(\delta_y\). Ad esempio, se consideriamo una bilancia imprecisa, ogni misura del peso corporeo è influenzata sia dal peso vero che dall’errore di misura della bilancia, che varia casualmente da misura a misura. In tal caso, il modello di analisi fattoriale sarebbe espresso come:
In questo modo, si può stimare il punteggio vero latente \(\xi\) e la componente di errore di misura latente \(\delta\), se si dispone di molte misure osservate \(y\), tutte che esprimono lo stesso costrutto latente \(\xi\).
8.2. Modello monofattoriale#
Con \(p\) variabili manifeste \(y_i\), il caso più semplice è quello di un solo fattore comune:
dove \(\xi\) rappresenta il fattore comune a tutte le \(y_i\), \(\delta_i\) sono i fattori specifici o unici di ogni variabile osservata e \(\lambda_i\) sono le saturazioni (o pesi) fattoriali le quali stabiliscono il peso del fattore latente su ciascuna variabile osservata.
Il modello di analisi fattoriale e il modello di regressione possono sembrare simili, ma presentano alcune differenze importanti. In primo luogo, sia il fattore comune \(\xi\) sia i fattori specifici \(\delta_i\) sono inosservabili, il che rende tutto ciò che si trova a destra dell’uguaglianza incognito. In secondo luogo, l’analisi di regressione e l’analisi fattoriale hanno obiettivi diversi. L’analisi di regressione mira a individuare le variabili esplicative, osservabili direttamente, che sono in grado di spiegare la maggior parte della varianza della variabile dipendente. Al contrario, il problema dell’analisi unifattoriale consiste nell’identificare la variabile esplicativa inosservabile che è in grado di spiegare la maggior parte della covarianza tra le variabili osservate.
Solitamente, per comodità, si assume che la media delle variabili osservate \(y_i\) sia zero, ovvero \(\mu_i=0\). Ciò equivale a considerare gli scarti delle variabili rispetto alle rispettive medie. Il modello unifattoriale assume che le variabili osservate siano il risultato della combinazione lineare di un fattore comune \(\xi\) e dei fattori specifici \(\delta_i\), ovvero:
dove \(\lambda_i\) è la saturazione o il peso della variabile \(i\)-esima sul fattore comune e \(\delta_i\) rappresenta il fattore specifico della variabile \(i\)-esima. Si assume che il fattore comune abbia media zero e varianza unitaria, mentre i fattori specifici abbiano media zero, varianza \(\psi_{i}\) e siano incorrelati tra loro e con il fattore comune. Nel modello unifattoriale, l’interdipendenza tra le variabili è completamente spiegata dal fattore comune.
Le ipotesi precedenti consentono di ricavare la covarianza tra la variabile osservata \(y_i\) e il fattore comune, la varianza della variabile osservata \(y_i\) e la covarianza tra due variabili osservate \(y_i\) e \(y_k\). L’obiettivo della discussione in questo capitolo è appunto quello di analizzare tali grandezze statistiche.
8.3. Correlazione parziale#
Prima di entrare nel dettaglio del modello statistico dell’analisi fattoriale, è importante chiarire il concetto di correlazione parziale. Si attribuisce spesso a Charles Spearman la nascita dell’analisi fattoriale. Nel 1904, Spearman pubblicò un articolo intitolato “General Intelligence, Objectively Determined and Measured” in cui propose la Teoria dei Due Fattori. In questo articolo, dimostrò come fosse possibile identificare un fattore inosservabile a partire da una matrice di correlazioni, utilizzando il metodo dell’annullamento della tetrade (tetrad differences). L’annullamento della tetrade è un’applicazione della teoria della correlazione parziale, che mira a stabilire se, controllando un insieme di variabili inosservabili chiamate fattori \(\xi_j\), le correlazioni tra le variabili osservabili \(Y_i\), al netto degli effetti lineari delle \(\xi_j\), diventino statisticamente nulle.
Possiamo considerare un esempio con tre variabili: \(Y_1\), \(Y_2\) e \(F\). La correlazione tra \(Y_1\) e \(Y_2\), \(r_{1,2}\), può essere influenzata dalla presenza di \(F\). Per calcolare la correlazione parziale tra \(Y_1\) e \(Y_2\) al netto dell’effetto lineare di \(F\), dobbiamo trovare le componenti di \(Y_1\) e \(Y_2\) che sono linearmente indipendenti da \(F\).
Per fare ciò, dobbiamo trovare la componente di \(Y_1\) che è ortogonale a \(F\). Possiamo calcolare i residui \(E_1\) del modello:
La componente di \(Y_1\) linearmente indipendente da \(F\) è quindi data dai residui \(E_1\). Possiamo eseguire un’operazione analoga per \(Y_2\) per trovare la sua componente ortogonale a \(F\). Calcolando la correlazione tra le due componenti così ottenute si ottiene la correlazione parziale tra \(Y_1\) e \(Y_2\) al netto dell’effetto lineare di \(F\).
L’eq. (8.3) consente di calcolare la correlazione parziale tra \(Y_1\) e \(Y_2\) al netto dell’effetto di \(F\) a partire dalle correlazioni semplici tra le tre variabili \(Y_1\), \(Y_2\) e \(F\).
In particolare, la correlazione parziale \(r_{1,2 \mid F}\) è data dalla differenza tra la correlazione \(r_{12}\) tra \(Y_1\) e \(Y_2\) e il prodotto tra le correlazioni \(r_{1F}\) e \(r_{2F}\) tra ciascuna delle due variabili e \(F\), il tutto diviso per la radice quadrata del prodotto delle differenze tra 1 e i quadrati delle correlazioni tra \(Y_1\) e \(F\) e tra \(Y_2\) e \(F\). In altre parole, la formula tiene conto dell’effetto di \(F\) sulle correlazioni tra \(Y_1\) e \(Y_2\) per ottenere una stima della relazione diretta tra le due variabili, eliminando l’effetto del fattore comune.
Consideriamo un esempio numerico. Sia \(f\) una variabile su cui misuriamo \(n\) valori
set.seed(123)
n <- 1000
f <- rnorm(n, 24, 12)
Siano \(y_1\) e \(y_2\) funzioni lineari di \(f\), a cui viene aggiunta una componente d’errore gaussiano:
y1 <- 10 + 7 * f + rnorm(n, 0, 50)
y2 <- 3 + 2 * f + rnorm(n, 0, 50)
La correlazione tra \(y_1\) e \(y_2\) (\(r_{12}= 0.355\)) deriva dal fatto che \(\hat{y}_1\) e \(\hat{y}_2\) sono entrambe funzioni lineari di \(f\):
Y <- cbind(y1, y2, f)
R <- cor(Y)
round(R, 3)
| y1 | y2 | f | |
|---|---|---|---|
| y1 | 1.000 | 0.380 | 0.867 |
| y2 | 0.380 | 1.000 | 0.423 |
| f | 0.867 | 0.423 | 1.000 |
Eseguiamo le regressioni di \(y_1\) su \(f\) e di \(y_2\) su \(F\):
fm1 <- lm(y1 ~ f)
fm2 <- lm(y2 ~ f)
Nella regressione, ciascuna osservazione \(y_{i1}\) viene scomposta in due componenti linearmente indipendenti, i valori adattati \(\hat{y}_{i}\) e i residui, \(e_{i}\): \(y_i = \hat{y}_i + e_1\). Nel caso di \(y_1\) abbiamo
round(head(cbind(y1, y1.hat=fm1$fit, e=fm1$res, fm1$fit+fm1$res)), 3)
| y1 | y1.hat | e | ||
|---|---|---|---|---|
| 1 | 81.130 | 130.505 | -49.375 | 81.130 |
| 2 | 106.667 | 159.704 | -53.037 | 106.667 |
| 3 | 308.032 | 317.846 | -9.813 | 308.032 |
| 4 | 177.314 | 186.285 | -8.971 | 177.314 |
| 5 | 61.393 | 191.482 | -130.089 | 61.393 |
| 6 | 374.094 | 331.668 | 42.426 | 374.094 |
Lo stesso può dirsi di \(y_2\). La correlazione parziale \(r_{12 \mid f}\) tra \(y_1\) e \(y_2\) dato \(f\) è uguale alla correlazione di Pearson tra i residui \(e_1\) e \(e_2\) calcolati mediante i due modelli di regressione descritti sopra:
cor(fm1$res, fm2$res)
La correlazione parziale tra \(y_1\) e \(y_2\) al netto di \(f\) è .02829.
Per i dati esaminati sopra, dunque, la correlazione parziale tra le variabili \(y_1\) e \(y_2\) diventa uguale a zero se la variabile \(f\) viene controllata (ovvero, se escludiamo da \(y_1\) e da \(y_2\) l’effetto lineare di \(f\)). Il fatto che la correlazione parziale sia zero significa che la correlazione che abbiamo osservato tra \(y_1\) e \(y_2\) (\(r = 0.355\)) non dipendeva dall’effetto che una variabile \(y\) esercitava sull’altra, ma bensì dal fatto che c’era una terza variabile, \(f\), che influenzava sia \(y_1\) sia \(y_2\). In altre parole, le variabili \(y_1\) e \(y_2\) sono condizionalmente indipendenti dato \(f\). Ciò significa, come abbiamo visto sopra, che la componente di \(y_1\) linearmente indipendente da \(f\) è incorrelata con la componente di \(y_2\) linearmente indipendente da \(f\).
La correlazione che abbiamo calcolato tra i residui di due modelli di regressione è identica alla correlazione che viene calcolata applicando l’eq. (8.3):
(R[1, 2] - R[1, 3] * R[2, 3]) /
sqrt((1 - R[1, 3]^2) * (1- R[2, 3]^2)) %>%
round(3)
In conclusione, possiamo attribuire all’eq. (8.3) la seguente interpretazione: la correlazione parziale tra le variabili \(y_1\) e \(y_2\) condizionata alla variabile \(f\) rappresenta la correlazione tra le componenti di \(y_1\) e \(y_2\) da cui è stato rimosso l’effetto lineare di \(f\). Ricordiamo il ragionamento che abbiamo svolto in precedenza per fornire un’interpretazione al coefficiente parziale del modello di regressione.
8.4. Principio base dell’analisi fattoriale#
Nell’attuale pratica dell’inferenza statistica nell’analisi fattoriale, spesso si utilizzano stime della massima verosimiglianza, calcolate attraverso procedure iterative come l’algoritmo EM (Rubin & Thayer, 1982). Tuttavia, all’inizio dell’analisi fattoriale, la procedura di estrazione dei fattori si basava sulle relazioni invarianti che il modello fattoriale imponeva agli elementi della matrice di covarianza delle variabili osservate. Uno dei più noti tra questi invarianti è la tetrade, presente nei modelli ad un fattore.
La tetrade consiste in una combinazione di quattro correlazioni. Se l’associazione tra le variabili osservate dipende dal fatto che queste sono state generate causalmente da un fattore comune inosservabile, allora è possibile generare una combinazione delle correlazioni che annulla la tetrade. In altre parole, l’analisi fattoriale si propone di individuare un insieme di sole \(m<p\) variabili latenti che, al netto dei fattori comuni, annullano significativamente tutte le correlazioni parziali tra le \(p\) variabili osservate. Se il metodo della correlazione parziale consente di identificare \(m\) variabili latenti, allora lo psicologo può concludere che tali fattori corrispondono agli \(m\) costrutti che intende misurare.
Per illustrare il metodo dell’annullamento della tetrade, consideriamo la matrice di correlazioni riportata nella Tabella seguente.
\(\xi\) |
\(y_1\) |
\(y_2\) |
\(y_3\) |
\(y_4\) |
\(y_5\) |
|
|---|---|---|---|---|---|---|
\(\xi\) |
1.00 |
|||||
\(y_1\) |
0.90 |
1.00 |
||||
\(y_2\) |
0.80 |
0.72 |
1.00 |
|||
\(y_3\) |
0.70 |
0.63 |
0.56 |
1.00 |
||
\(y_4\) |
0.60 |
0.54 |
0.48 |
0.42 |
1.00 |
|
\(y_5\) |
0.50 |
0.45 |
0.40 |
0.35 |
0.30 |
1.00 |
Matrice di correlazioni nella quale tutte le correlazioni parziali tra le variabili \(Y\) al netto dell’effetto di \(\xi\) sono nulle.
Nella tabella, la correlazione parziale tra ciascuna coppia di variabili \(y_i\), \(y_j\) (con \(i \neq j\)) dato \(\xi\) è sempre pari a zero. Ad esempio, la correlazione parziale tra \(y_3\) e \(y_5\) condizionata a \(\xi\) è:
Lo stesso risultato si trova per qualunque altra coppia di variabili \(y_i\) e \(y_j\), ovvero \(r_{ij \mid \xi} = 0\). Possiamo dunque dire che, per la matrice di correlazioni della Tabella, esiste un’unica variabile \(\xi\) la quale, quando viene controllata, spiega tutte le
correlazioni tra le variabili \(y\). Questo risultato non è sorprendente, in quanto la matrice di correlazioni è stata costruita in modo tale da possedere tale proprietà.
Immaginiamo invece di trovarci in una situazione diversa, ovvero di avere a disposizione solo le variabili \(y_i\) senza conoscere \(\xi\). In questo caso, ci poniamo la domanda: “Esiste una variabile latente \(\xi\) tale che, se fosse osservabile, renderebbe nulle tutte le correlazioni parziali tra le variabili \(y\)?”. Se esiste una tale variabile latente che spiega tutte le correlazioni tra le variabili osservate \(y\), allora viene chiamata fattore latente.
Un fattore è una variabile inosservabile in grado di rendere significativamente nulle tutte le correlazioni parziali tra le variabili manifeste.
8.4.1. Vincoli sulle correlazioni#
Come si può stabilire se esiste una variabile inosservabile in grado di rendere nulle tutte le correlazioni parziali tra le variabili osservate? Riscriviamo l’eq. (8.3) per specificare la correlazione parziale tra le variabili \(y_i\) e \(y_j\) dato \(\xi\):
Affinché \(r_{ij \mid \xi}\) sia uguale a zero è necessario che
ovvero
In altri termini, se esiste un fattore non osservato \(\xi\) in grado di rendere uguali a zero tutte le correlazioni parziali \(r_{ih \mid \xi}\), allora la correlazione tra ciascuna coppia di variabili \(y\) deve essere uguale al prodotto delle correlazioni tra ciascuna \(y\) e il fattore latente \(\xi\). Questo è il principio base dell’analisi fattoriale.
8.4.2. Teoria dei Due Fattori#
Per fornire un esempio concreto del metodo dell’annullamento della tetrade, possiamo esaminare la matrice di correlazioni utilizzata da Spearman (1904) nella sua ricerca sulle capacità intellettuali di alcuni studenti di una scuola superiore. In particolare, sono state considerate le prestazioni degli studenti in tre materie scolastiche (studio dei classici, letteratura inglese, abilità matematiche) e in un compito di discriminazione dell’altezza di suoni. Secondo la Teoria dei Due Fattori di Spearman, le prestazioni in ogni compito intellettuale sono costituite da due componenti: un fattore generale comune a tutte le attività intellettuali (fattore “g”) e un fattore specifico relativo al compito in questione (fattore “s”). In questo modello, il fattore “g” rappresenta la componente invariante dell’abilità intellettiva, mentre il fattore “s” è una componente che varia da condizione a condizione.
Per verificare l’esistenza di una variabile latente in grado di spiegare le correlazioni tra le variabili osservate da Spearman, è stato proposto uno strumento chiamato “annullamento della tetrade”. Tale strumento si basa sui vincoli sulle correlazioni derivanti dalla definizione di correlazione parziale. Come abbiamo visto in precedenza, la correlazione parziale tra le variabili \(y\) indicizzate da \(i\) e \(j\), al netto dell’effetto di \(\xi\), è nulla se la seguente relazione è soddisfatta:
In altre parole, se la correlazione tra due variabili osservate può essere spiegata dall’effetto di una terza variabile latente, allora la correlazione parziale tra tali variabili sarà nulla una volta che si tiene conto dell’effetto della variabile latente. Utilizzando questo strumento, Spearman ha dimostrato che le correlazioni tra le prestazioni degli studenti nei vari compiti intellettuali possono essere spiegate da due fattori: un fattore generale comune a tutti i compiti (fattore “g”) e un fattore specifico a ciascun compito (fattore “s”).
Nel caso dei dati di Spearman, le correlazioni parziali sono nulle quando la correlazione tra “studi classici” e “letteratura inglese” è pari al prodotto della correlazione tra “studi classici” e la variabile latente \(\xi\) e della correlazione tra “letteratura inglese” e la variabile latente \(\xi\). Inoltre, la correlazione tra “studi classici” e “abilità matematica” deve essere uguale al prodotto della correlazione tra “studi classici” e la variabile latente \(\xi\) e della correlazione tra “abilità matematica” e la variabile latente \(\xi\), e così via per tutte le altre coppie di variabili.
Le correlazioni tra le variabili manifeste e il fattore latente sono dette saturazioni fattoriali e vengono denotate con la lettera \(\lambda\). Se il modello di Spearman è corretto, avremo che
dove \(r_{ec}\) è la correlazione tra “letteratura inglese” (e) e “studi classici” (c), \(\lambda_e\) è la correlazione tra “letteratura inglese” e \(\xi\), e \(\lambda_{c}\) è la correlazione tra “studi classici” e \(\xi\).
Allo stesso modo, la correlazione tra “studi classici” e “matematica” (m) dovrà essere uguale a
eccetera.
8.4.3. Annullamento della tetrade#
Utilizzando il metodo dell’annullamento della tetrade è possibile stimare i valori delle saturazioni fattoriali \(\lambda\), partendo dalle correlazioni tra le tre coppie di variabili manifeste \(c\), \(m\) ed \(e\). In particolare, si possono scrivere tre equazioni in tre incognite, che consentono di calcolare le saturazioni \(\lambda\). Ad esempio, per le tre variabili sopracitate, tali equazioni possono essere espresse nel seguente modo:
Calcolando il determinante del sistema di equazioni lineari composto dalle correlazioni tra le variabili manifeste \(c\), \(m\) ed \(e\), possiamo ottenere il valore della saturazione fattoriale \(\lambda\) e, in particolare, il coefficiente di saturazione \(\lambda_m\) della variabile \(y_m\) nel fattore comune \(\xi\). In altre parole, risolvendo il sistema di equazioni lineari, possiamo stimare il valore delle saturazioni fattoriali, compreso il coefficiente di saturazione \(\lambda_m\), a partire dalle correlazioni tra le variabili manifeste:
Lo stesso vale per le altre due saturazioni \(\lambda_c\) e \(\lambda_e\).
Nel suo articolo del 1904, Spearman osservò le seguenti correlazioni tra le variabili \(Y_c\), \(Y_e\), \(Y_m\) e \(Y_p\):
Utilizzando l’eq. (8.4), mediante le correlazioni \(r_{cm}\), \(r_{em}\), e \(r_{ce}\) fornite dalla tabella precedente, la saturazione \(\lambda_m\) diventa uguale a:
È importante notare che il metodo dell’annullamento della tetrade produce risultati falsificabili. Infatti, ci sono modi diversi per calcolare la stessa saturazione fattoriale. Se il modello fattoriale è corretto si deve ottenere lo stesso risultato in tutti i casi. Nel caso presente, la saturazione fattoriale \(\lambda_m\) può essere calcolata in altri due modi:
I tre valori che sono stati ottenuti sono molto simili. Qual è allora la stima migliore di \(\lambda_m\)?
8.4.4. Metodo del centroide#
La soluzione più semplice è quella di fare la media di questi tre valori (\(\bar{\lambda}_m = 0.73\)). Un metodo migliore (meno vulnerabile ai valori anomali) è dato dal rapporto tra la somma dei numeratori e dei denominatori:
In questo caso, i due metodi danno lo stesso risultato. Le altre tre saturazioni fattoriali trovate mediante il metodo del centroide sono:
In conclusione,
8.5. Introduzione a lavaan#
8.5.1. Sintassi del modello#
Al cuore del pacchetto lavaan si trova la “sintassi del modello”. La sintassi del modello è una descrizione del modello da stimare. In questa sezione, spieghiamo brevemente gli elementi della sintassi del modello lavaan.
Nell’ambiente R, una formula di regressione ha la seguente forma:
y ~ x1 + x2 + x3 + x4
In questa formula, la tilde (“~”) è l’operatore di regressione. Sul lato sinistro dell’operatore, abbiamo la variabile dipendente (y), e sul lato destro abbiamo le variabili indipendenti, separate dall’operatore “+” . In lavaan, un modello tipico è semplicemente un insieme (o sistema) di formule di regressione, in cui alcune variabili (che iniziano con una ‘f’ qui sotto) possono essere latenti. Ad esempio:
y ~ f1 + f2 + x1 + x2
f1 ~ f2 + f3
f2 ~ f3 + x1 + x2
Se abbiamo variabili latenti in una qualsiasi delle formule di regressione, dobbiamo “definirle” elencando i loro indicatori (manifesti o latenti). Lo facciamo utilizzando l’operatore speciale “=~”, che può essere letto come “è misurato da”. Ad esempio, per definire le tre variabili latenti f1, f2 e f3, possiamo usare qualcosa del genere:
f1 =~ y1 + y2 + y3
f2 =~ y4 + y5 + y6
f3 =~ y7 + y8 + y9 + y10
Inoltre, le varianze e le covarianze sono specificate utilizzando un operatore “doppia tilde”, ad esempio:
y1 ~~ y1 # varianza
y1 ~~ y2 # covarianza
f1 ~~ f2 # covarianza
E infine, le intercette per le variabili osservate e latenti sono semplici formule di regressione con solo una intercetta (esplicitamente indicato dal numero “1”) come unico predittore:
y1 ~ 1
f1 ~ 1
Utilizzando questi quattro tipi di formule, è possibile descrivere una vasta gamma di modelli di variabili latenti. L’attuale insieme di tipi di formula è riassunto nella tabella sottostante.
tipo di formula |
operatore |
mnemonic |
|---|---|---|
definizione variabile latente |
=~ |
è misurato da |
regressione |
~ |
viene regredito su |
(co)varianza (residuale) |
~~ |
è correlato con |
intercetta |
~ 1 |
intercetta |
Una sintassi completa del modello lavaan è semplicemente una combinazione di questi tipi di formule, racchiusi tra virgolette singole. Ad esempio:
my_model <- '
# regressions
y1 + y2 ~ f1 + f2 + x1 + x2
f1 ~ f2 + f3
f2 ~ f3 + x1 + x2
# latent variable definitions
f1 =~ y1 + y2 + y3
f2 =~ y4 + y5 + y6
f3 =~ y7 + y8 + y9
# variances and covariances
y1 ~~ y1
y1 ~~ y2
f1 ~~ f2
# intercepts
y1 ~ 1
f1 ~ 1
'
Per adattare il modello ai dati usiamo la seguente sintassi.
fit <- cfa(model = my_model, data = my_data)
8.5.2. Un esempio concreto#
Analizziamo nuovamente i dati di Spearman che abbiamo esaminato in precedenza usando lavaan. La matrice completa dei dati di Spearman è messa a disposizione da @kan2019extending. Iniziamo a caricare i pacchetti necessari:
library("lavaan")
library("semPlot")
library("knitr")
library("kableExtra")
library("tidyr")
library("corrplot")
This is lavaan 0.6-15
lavaan is FREE software! Please report any bugs.
Attaching package: ‘kableExtra’
The following object is masked from ‘package:dplyr’:
group_rows
corrplot 0.92 loaded
Specifichiamo il nome delle variabili manifeste
varnames <- c(
"Classics", "French", "English", "Math", "Pitch", "Music"
)
e il loro numero
ny <- length (varnames)
Creiamo la matrice di correlazione:
spearman_cor_mat <- matrix(
c(
1.00, .83, .78, .70, .66, .63,
.83, 1.00, .67, .67, .65, .57,
.78, .67, 1.00, .64, .54, .51,
.70, .67, .64, 1.00, .45, .51,
.66, .65, .54, .45, 1.00, .40,
.63, .57, .51, .51, .40, 1.00
),
ny, ny,
byrow = TRUE,
dimnames = list(varnames, varnames)
)
Specifichiamo l’ampiezza campionaria:
n <- 33
Definiamo il modello unifattoriale in lavaan. L’operatore =~ si può leggere dicendo che la variabile latente a sinistra dell’operatore viene identificata dalle variabili manifeste elencate a destra dell’operatore e separate dal segno +. Per il caso presente, il modello dei due fattori di Spearman può essere specificato come segue.
spearman_mod <- "
g =~ Classics + French + English + Math + Pitch + Music
"
Adattiamo il modello ai dati con la funzione cfa():
fit1 <- lavaan::cfa(
spearman_mod,
sample.cov = spearman_cor_mat,
sample.nobs = n,
std.lv = TRUE
)
La funzione cfa() è una funzione dedicata per adattare modelli di analisi fattoriale confermativa. Il primo argomento è il modello specificato dall’utente. Il secondo argomento è il dataset che contiene le variabili osservate. L’argomento std.lv = TRUE specifica che imponiamo una varianza pari a 1 a tutte le variabili latenti comuni (nel caso presente, solo una). Ciò consente di stimare le saturazioni fattoriali.
Una volta adattato il modello, la funzione summary() ci consente di esaminare la soluzione ottenuta:
out = summary(
fit1,
fit.measures = TRUE,
standardized = TRUE
)
print(out)
lavaan 0.6.15 ended normally after 23 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 12
Number of observations 33
Model Test User Model:
Test statistic 2.913
Degrees of freedom 9
P-value (Chi-square) 0.968
Model Test Baseline Model:
Test statistic 133.625
Degrees of freedom 15
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 1.000
Tucker-Lewis Index (TLI) 1.086
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -212.547
Loglikelihood unrestricted model (H1) -211.091
Akaike (AIC) 449.094
Bayesian (BIC) 467.052
Sample-size adjusted Bayesian (SABIC) 429.622
Root Mean Square Error of Approximation:
RMSEA 0.000
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.000
P-value H_0: RMSEA <= 0.050 0.976
P-value H_0: RMSEA >= 0.080 0.016
Standardized Root Mean Square Residual:
SRMR 0.025
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
g =~
Classics 0.942 0.129 7.314 0.000 0.942 0.956
French 0.857 0.137 6.239 0.000 0.857 0.871
English 0.795 0.143 5.545 0.000 0.795 0.807
Math 0.732 0.149 4.923 0.000 0.732 0.743
Pitch 0.678 0.153 4.438 0.000 0.678 0.689
Music 0.643 0.155 4.142 0.000 0.643 0.653
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Classics 0.083 0.051 1.629 0.103 0.083 0.086
.French 0.234 0.072 3.244 0.001 0.234 0.242
.English 0.338 0.094 3.610 0.000 0.338 0.349
.Math 0.434 0.115 3.773 0.000 0.434 0.447
.Pitch 0.510 0.132 3.855 0.000 0.510 0.526
.Music 0.556 0.143 3.893 0.000 0.556 0.573
g 1.000 1.000 1.000
L’output consiste in tre parti. Le prime nove righe sono chiamate intestazione. L’intestazione contiene le seguenti informazioni:
il numero di versione di lavaan
se l’ottimizzazione è terminata normalmente o meno e quante iterazioni sono state necessarie
lo stimatore utilizzato (qui: ML, per la massima verosimiglianza)
l’ottimizzatore utilizzato per trovare i valori dei parametri di adattamento migliori per questo stimatore (qui: NLMINB)
il numero di parametri del modello (qui: 12)
il numero di osservazioni che sono state effettivamente utilizzate nell’analisi (qui: 33)
una sezione chiamata “Model Test User Model”: che fornisce una statistica di test, i gradi di libertà e un valore p per il modello specificato dall’utente.
La sezione successiva contiene ulteriori misure di adattamento e viene mostrata solo se si utilizza l’argomento opzionale fit.measures = TRUE. Inizia con la riga Model Test Baseline Model: e termina con il valore per l’SRMR. L’ultima sezione contiene le stime dei parametri. Inizia con informazioni (tecniche) sul metodo utilizzato per calcolare gli errori standard. Quindi, vengono elencati tutti i parametri liberi (e fissati) inclusi nel modello. Di solito, prima vengono mostrate le variabili latenti, seguite dalle covarianze e dalle varianze (residui). La prima colonna (Stima) contiene il valore del parametro (stimato o fisso) per ogni parametro del modello; la seconda colonna (Std.err) contiene l’errore standard per ogni parametro stimato; la terza colonna (Z-value) contiene la statistica di Wald (che viene semplicemente ottenuta dividendo il valore del parametro per il suo errore standard), e l’ultima colonna (P(>|z|)) contiene il valore p per testare l’ipotesi nulla che il valore del parametro sia uguale a zero nella popolazione.
Si noti che nella sezione Varianze: c’è un punto prima dei nomi delle variabili osservate. Ciò perché sono variabili dipendenti (o endogene) (predette dalle variabili latenti) e quindi il valore della varianza stampato in output è una stima della varianza residua: la varianza rimanente che non è spiegata dal/i predittore/i. Al contrario, non c’è un punto prima dei nomi delle variabili latenti, perché in questo modello sono variabili esogene. I valori delle varianze qui sono le varianze totali stimate delle variabili latenti.
È possibile semplificare l’output dalla funzione summary() in maniera tale da stampare solo la tabella completa delle stime dei parametri e degli errori standard. Qui usiamo coef(fit1).
print(round(coef(fit1), 2))
g=~Classics g=~French g=~English g=~Math
0.94 0.86 0.79 0.73
g=~Pitch g=~Music Classics~~Classics French~~French
0.68 0.64 0.08 0.23
English~~English Math~~Math Pitch~~Pitch Music~~Music
0.34 0.43 0.51 0.56
Usando parameterEstimates, l’output diventa il seguente.
out = parameterEstimates(fit1, standardized = TRUE)
print(out)
lhs op rhs est se z pvalue ci.lower ci.upper std.lv
1 g =~ Classics 0.942 0.129 7.314 0.000 0.689 1.194 0.942
2 g =~ French 0.857 0.137 6.239 0.000 0.588 1.127 0.857
3 g =~ English 0.795 0.143 5.545 0.000 0.514 1.076 0.795
4 g =~ Math 0.732 0.149 4.923 0.000 0.441 1.024 0.732
5 g =~ Pitch 0.678 0.153 4.438 0.000 0.379 0.978 0.678
6 g =~ Music 0.643 0.155 4.142 0.000 0.339 0.948 0.643
7 Classics ~~ Classics 0.083 0.051 1.629 0.103 -0.017 0.183 0.083
8 French ~~ French 0.234 0.072 3.244 0.001 0.093 0.376 0.234
9 English ~~ English 0.338 0.094 3.610 0.000 0.154 0.522 0.338
10 Math ~~ Math 0.434 0.115 3.773 0.000 0.208 0.659 0.434
11 Pitch ~~ Pitch 0.510 0.132 3.855 0.000 0.251 0.769 0.510
12 Music ~~ Music 0.556 0.143 3.893 0.000 0.276 0.836 0.556
13 g ~~ g 1.000 0.000 NA NA 1.000 1.000 1.000
std.all std.nox
1 0.956 0.956
2 0.871 0.871
3 0.807 0.807
4 0.743 0.743
5 0.689 0.689
6 0.653 0.653
7 0.086 0.086
8 0.242 0.242
9 0.349 0.349
10 0.447 0.447
11 0.526 0.526
12 0.573 0.573
13 1.000 1.000
Con opportuni parametri possiamo semplificare l’output nel modo seguente.
out = parameterEstimates(fit1, standardized = TRUE) %>%
dplyr::filter(op == "=~") %>%
dplyr::select(
"Latent Factor" = lhs,
Indicator = rhs,
B = est,
SE = se,
Z = z,
"p-value" = pvalue,
Beta = std.all
)
print(out)
Latent.Factor Indicator B SE Z p.value Beta
1 g Classics 0.942 0.129 7.314 0 0.956
2 g French 0.857 0.137 6.239 0 0.871
3 g English 0.795 0.143 5.545 0 0.807
4 g Math 0.732 0.149 4.923 0 0.743
5 g Pitch 0.678 0.153 4.438 0 0.689
6 g Music 0.643 0.155 4.142 0 0.653
Esaminiamo la matrice delle correlazioni residue:
cor_table <- residuals(fit1, type = "cor")$cov
print(cor_table)
Clsscs French Englsh Math Pitch Music
Classics 0.000
French -0.003 0.000
English 0.008 -0.033 0.000
Math -0.011 0.023 0.040 0.000
Pitch 0.001 0.050 -0.016 -0.062 0.000
Music 0.005 0.001 -0.017 0.024 -0.050 0.000
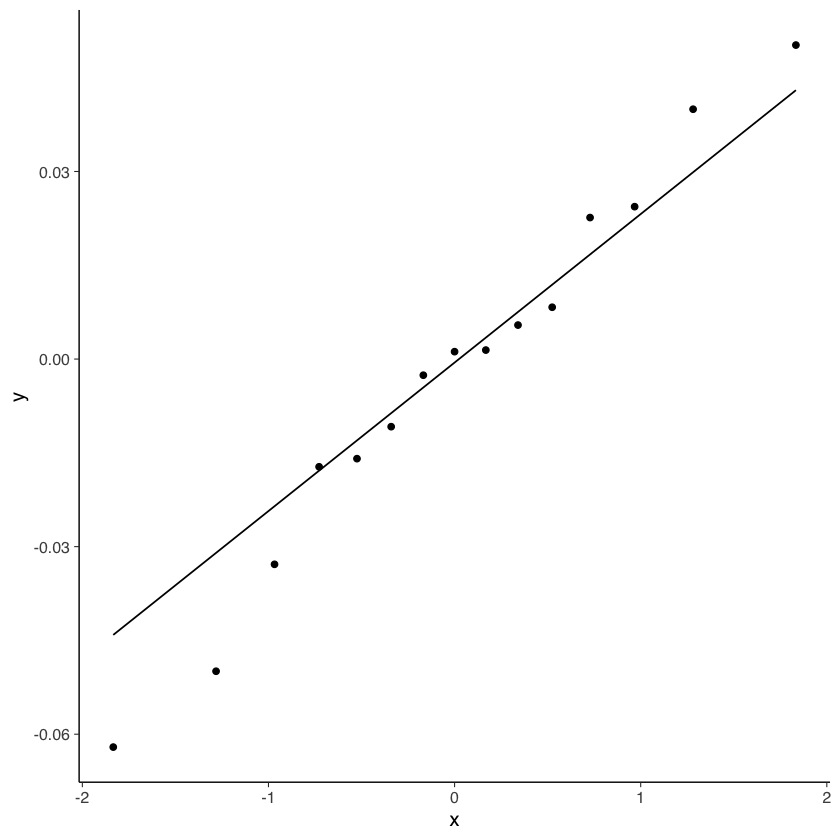
Creiamo un qq-plot dei residui:
res1 <- residuals(fit1, type = "cor")$cov
res1[upper.tri(res1, diag = TRUE)] <- NA
v1 <- as.vector(res1)
v2 <- v1[!is.na(v1)]
tibble(v2) %>%
ggplot(aes(sample = v2)) +
stat_qq() +
stat_qq_line()
8.5.3. Diagrammi di percorso#
Il pacchetto semPlot consente di disegnare diagrammi di percorso per vari modelli SEM. La funzione semPaths prende in input un oggetto creato da lavaan e disegna il diagramma, con diverse opzioni disponibili. Il diagramma prodotto controlla le dimensioni dei caratteri/etichette, la visualizzazione dei residui e il colore dei percorsi/coefficienti. Sono disponibili queste e molte altre opzioni di controllo.
nice_lavaanPlot(fit1, stand = TRUE, stars= FALSE, covs = TRUE)
Il calcolo delle saturazioni fattoriali con il metodo del centroide aveva prodotto il seguente risultato:
classici (Cls): 0.97
inglese (Eng): 0.84
matematica (Mth): 0.73
pitch discrimination (Ptc): 0.65
Si noti la somiglianza con i valori ottenuti mediante il metodo di massima verosimiglianza riportati nella figura.
8.5.4. Analisi fattoriale esplorativa#
Quando abbiamo un’unica variabile latente, l’analisi fattoriale confermativa si riduce al caso dell’analisi fattoriale esplorativa. Esaminiamo qui sotto la sintassi per l’analisi fattoriale esplorativa in lavaan.
Specifichiamo il modello.
efa_model <- '
efa("efa")*g =~ Classics + French + English + Math + Pitch + Music
'
Adattiamo il modello ai dati.
fit2 <- lavaan::cfa(
efa_model,
sample.cov = spearman_cor_mat,
sample.nobs = n,
std.lv = TRUE
)
Esaminiamo la soluzione ottenuta.
out = summary(fit2, standardized = TRUE)
print(out)
lavaan 0.6.15 ended normally after 3 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 12
Rotation method GEOMIN OBLIQUE
Geomin epsilon 0.001
Rotation algorithm (rstarts) GPA (30)
Standardized metric TRUE
Row weights None
Number of observations 33
Model Test User Model:
Test statistic 2.913
Degrees of freedom 9
P-value (Chi-square) 0.968
Parameter Estimates:
Standard errors Standard
Information Expected
Information saturated (h1) model Structured
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
g =~ efa
Classics 0.942 0.129 7.314 0.000 0.942 0.956
French 0.857 0.137 6.239 0.000 0.857 0.871
English 0.795 0.143 5.545 0.000 0.795 0.807
Math 0.732 0.149 4.923 0.000 0.732 0.743
Pitch 0.678 0.153 4.438 0.000 0.678 0.689
Music 0.643 0.155 4.142 0.000 0.643 0.653
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.Classics 0.083 0.051 1.629 0.103 0.083 0.086
.French 0.234 0.072 3.244 0.001 0.234 0.242
.English 0.338 0.094 3.610 0.000 0.338 0.349
.Math 0.434 0.115 3.773 0.000 0.434 0.447
.Pitch 0.510 0.132 3.855 0.000 0.510 0.526
.Music 0.556 0.143 3.893 0.000 0.556 0.573
g 1.000 1.000 1.000
nice_lavaanPlot(fit2, stand = TRUE, stars= FALSE, covs = TRUE)
8.6. Conclusioni#
Nel presente capitolo abbiamo introdotto il metodo dell’annullamento della tetrade che consente di stimare le saturazioni di un modello monofattoriale. Abbiamo anche visto che il metodo dell’annullamento della tetrade non è altro che un’applicazione della correlazione parziale.
Possiamo dire che un tema cruciale nella costruzione dei test psicologici è quello di stabilire il numero di fattori/tratti che sono soggiacenti all’insieme degli indicatori che vengono considerati. La teoria classica dei test richiede che il test sia monofattoriale, ovvero che gli indicatori considerati siano l’espressione di un unico tratto latente. La violazione della monodimensionalità rende problematica l’applicazione dei principi della teoria classica dei test ai punteggi di un test che non possiede tale proprietà. L’esame della dimensionalità di un gruppo di indicatori rappresenta dunque una fase cruciale nel processo di costruzione di un test e, solitamente, questo esame è affrontato mediante l’analisi fattoriale. In questo capitolo abbiamo presentato le proprietà di base del modello unifattoriale.
