31. Curve di crescita latente#
31.1. Una applicazione concreta#
Esaminiamo l’adattamento di un modello LGM ad un campione di dati reali. In questo tutorial, considereremo il cambiamento nel rendimento in matematica dei bambini durante la scuola elementare e media utilizzando il set di dati NLSY-CYA [GRE16].
Iniziamo a leggere i dati.
#set filepath for data file
filepath <- "https://raw.githubusercontent.com/LRI-2/Data/main/GrowthModeling/nlsy_math_wide_R.dat"
# read in the text data file using the url() function
dat <- read.table(
file = url(filepath),
na.strings = "."
) # indicates the missing data designator
# copy data with new name
nlsy_math_wide <- dat
# Give the variable names
names(nlsy_math_wide) <- c(
"id", "female", "lb_wght", "anti_k1",
"math2", "math3", "math4", "math5", "math6", "math7", "math8",
"age2", "age3", "age4", "age5", "age6", "age7", "age8",
"men2", "men3", "men4", "men5", "men6", "men7", "men8",
"spring2", "spring3", "spring4", "spring5", "spring6", "spring7", "spring8",
"anti2", "anti3", "anti4", "anti5", "anti6", "anti7", "anti8"
)
# view the first few observations (and columns) in the data set
head(nlsy_math_wide[, 1:11], 10)
| id | female | lb_wght | anti_k1 | math2 | math3 | math4 | math5 | math6 | math7 | math8 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | |
| 1 | 201 | 1 | 0 | 0 | NA | 38 | NA | 55 | NA | NA | NA |
| 2 | 303 | 1 | 0 | 1 | 26 | NA | NA | 33 | NA | NA | NA |
| 3 | 2702 | 0 | 0 | 0 | 56 | NA | 58 | NA | NA | NA | 80 |
| 4 | 4303 | 1 | 0 | 0 | NA | 41 | 58 | NA | NA | NA | NA |
| 5 | 5002 | 0 | 0 | 4 | NA | NA | 46 | NA | 54 | NA | 66 |
| 6 | 5005 | 1 | 0 | 0 | 35 | NA | 50 | NA | 60 | NA | 59 |
| 7 | 5701 | 0 | 0 | 2 | NA | 62 | 61 | NA | NA | NA | NA |
| 8 | 6102 | 0 | 0 | 0 | NA | NA | 55 | 67 | NA | 81 | NA |
| 9 | 6801 | 1 | 0 | 0 | NA | 54 | NA | 62 | NA | 66 | NA |
| 10 | 6802 | 0 | 0 | 0 | NA | 55 | NA | 66 | NA | 68 | NA |
Il nostro interesse specifico riguarda il cambiamento relativo alle misure ripetute di matematica, da math2 a math8.
Selezioniamo le variabili di interesse.
nlsy_math_sub <- nlsy_math_wide |>
dplyr::select("id", "math2", "math3", "math4", "math5", "math6", "math7", "math8")
Trasformiamo i dati in formato long.
nlsy_math_long <- reshape(
data = nlsy_math_sub,
timevar = c("grade"),
idvar = "id",
varying = c(
"math2", "math3", "math4",
"math5", "math6", "math7", "math8"
),
direction = "long", sep = ""
)
Ordiniamo i dati in base alle variabili id e grade.
nlsy_math_long <- nlsy_math_long[order(nlsy_math_long$id, nlsy_math_long$grade), ]
Rimuoviamo gli NA dalla variabile math per potere generare il grafico con le traiettorie individuali di sviluppo
nlsy_math_long <- nlsy_math_long[which(is.na(nlsy_math_long$math) == FALSE), ]
Guardiamo prima i dati grezzi.
nlsy_math_long |>
ggplot(aes(x = grade, y = math)) +
geom_point(
size = 1.2,
alpha = .8,
# to add some random noise for plotting purposes
position = "jitter"
) +
labs(title = "PAT Mathematics as a function of Grade")
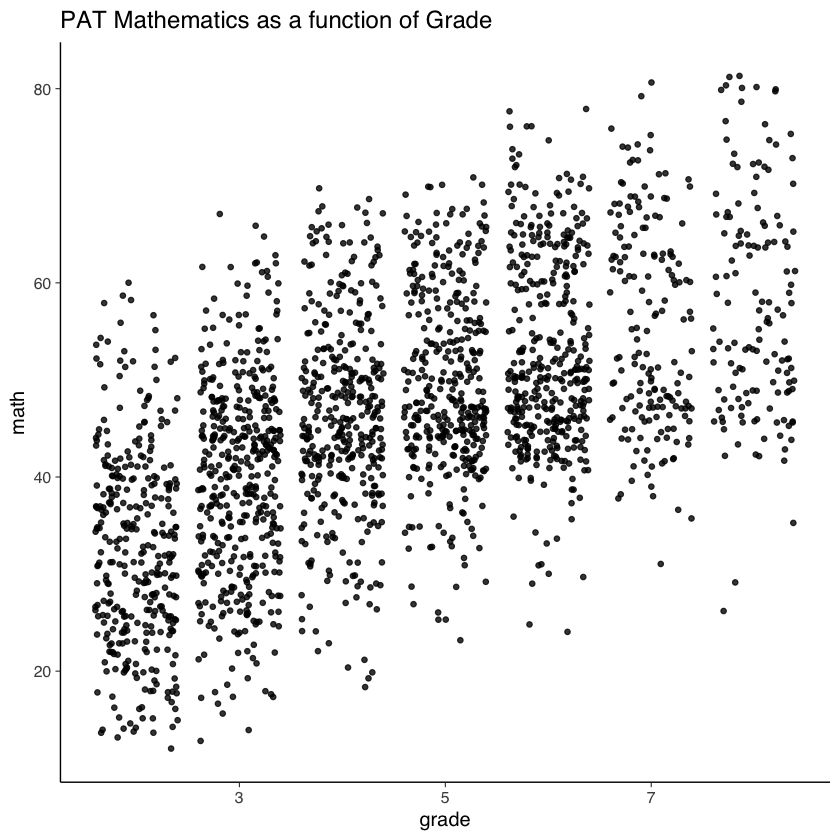
Aggiungiamo al grafico le retta dei minimi quadrati calcolata su tutti i dati (ignorando il ragruppamento dei dati in funzione dei partecipanti).
nlsy_math_long |>
ggplot(aes(x = grade, y = math)) +
geom_point(
size = 1.2,
alpha = .8,
# to add some random noise for plotting purposes
position = "jitter"
) +
geom_smooth(
method = lm,
se = FALSE,
col = "black",
linewidth = .5,
alpha = .8
) + # to add regression line
labs(title = "PAT Mathematics as a function of Grade")
`geom_smooth()` using formula = 'y ~ x'
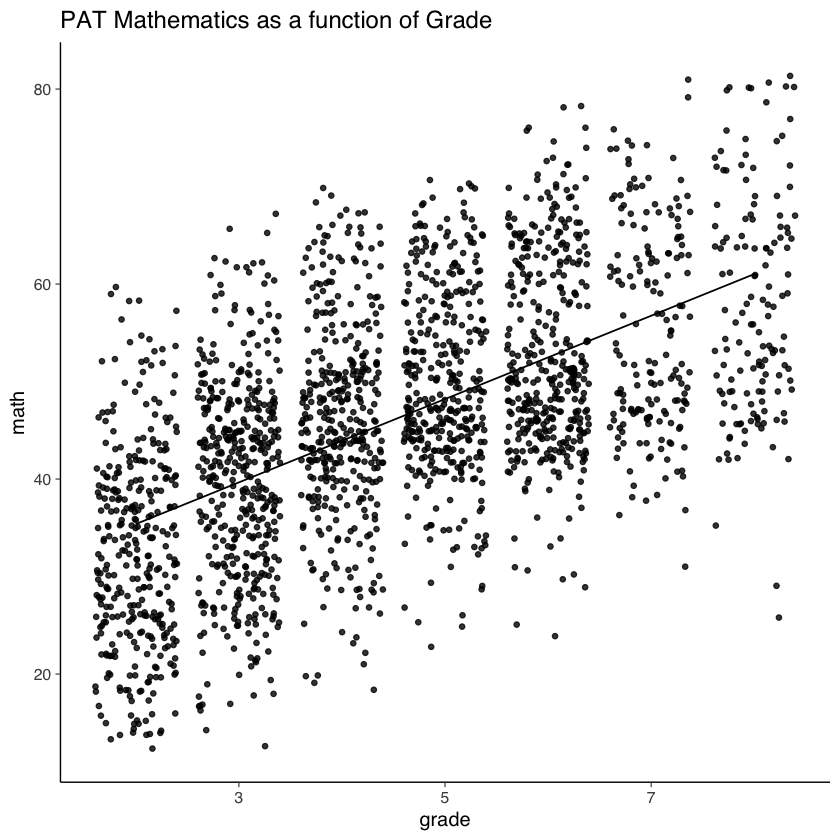
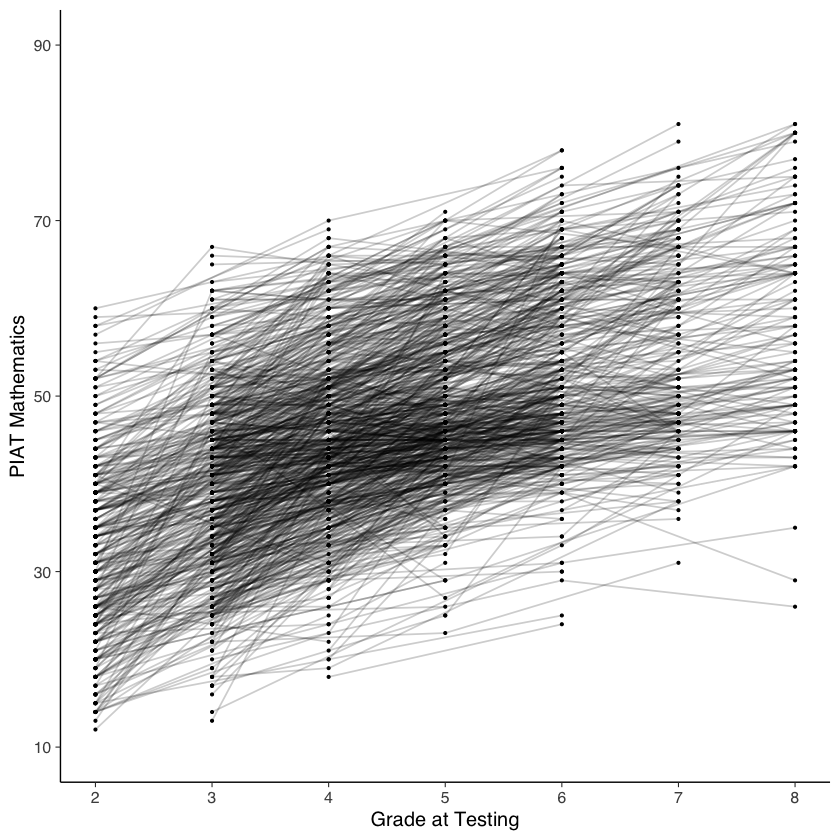
Esaminiamo le traiettorie di cambiamento intra-individuale.
# intraindividual change trajetories
nlsy_math_long |>
ggplot(
aes(x = grade, y = math, group = id)
) + # setting variables
geom_point(size = .5) + # adding points to plot
geom_line(alpha = 0.2) + # adding lines to plot
# setting the x-axis with breaks and labels
scale_x_continuous(
limits = c(2, 8),
breaks = c(2, 3, 4, 5, 6, 7, 8),
name = "Grade at Testing"
) +
# setting the y-axis with limits breaks and labels
scale_y_continuous(
limits = c(10, 90),
breaks = c(10, 30, 50, 70, 90),
name = "PIAT Mathematics"
)
31.2. Modello di assenza di crescita#
Come si può vedere dal grafico precedente, i punteggi di matematica sembrano aumentare nel tempo in modo sistematico. Per cominciare l’analisi, useremo un modello senza crescita come punto di riferimento con cui confrontare i modelli successivi.
Questo modello ipotizza che i punteggi di matematica degli individui siano costanti nel tempo e stima, per ogni individuo, il “valore vero” dei punteggi di matematica, senza considerare la variazione temporale. Non essendo in grado di prevedere la variazione temporale dei punteggi, questo modello descrive un caso di poco interesse e quindi è generalmente scartato.
Il modello senza crescita include una variabile latente e un’intercetta che rappresenta il livello generale di prestazione costante nel tempo.
Per definire il modello senza crescita, utilizzeremo la seguente sintassi di lavaan.
ng_math_lavaan_model <- '
# latent variable definitions
#intercept
eta_1 =~ 1*math2
eta_1 =~ 1*math3
eta_1 =~ 1*math4
eta_1 =~ 1*math5
eta_1 =~ 1*math6
eta_1 =~ 1*math7
eta_1 =~ 1*math8
# factor variances
eta_1 ~~ eta_1
# covariances among factors
#none (only 1 factor)
# factor means
eta_1 ~ start(30)*1
# manifest variances (made equivalent by naming theta)
math2 ~~ theta*math2
math3 ~~ theta*math3
math4 ~~ theta*math4
math5 ~~ theta*math5
math6 ~~ theta*math6
math7 ~~ theta*math7
math8 ~~ theta*math8
# manifest means (fixed at zero)
math2 ~ 0*1
math3 ~ 0*1
math4 ~ 0*1
math5 ~ 0*1
math6 ~ 0*1
math7 ~ 0*1
math8 ~ 0*1
' #end of model definition
Adattiamo il modello ai dati.
ng_math_lavaan_fit <- sem(ng_math_lavaan_model,
data = nlsy_math_wide,
meanstructure = TRUE,
estimator = "ML",
missing = "fiml"
)
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING: some cases are empty and will be ignored:
741”
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING:
due to missing values, some pairwise combinations have less than
10% coverage; use lavInspect(fit, "coverage") to investigate.”
Warning message in lav_mvnorm_missing_h1_estimate_moments(Y = X[[g]], wt = WT[[g]], :
“lavaan WARNING:
Maximum number of iterations reached when computing the sample
moments using EM; use the em.h1.iter.max= argument to increase the
number of iterations”
Esaminiamo la soluzione.
summary(ng_math_lavaan_fit, fit.measures = TRUE, standardized = TRUE) |>
print()
lavaan 0.6.15 ended normally after 18 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 9
Number of equality constraints 6
Used Total
Number of observations 932 933
Number of missing patterns 60
Model Test User Model:
Test statistic 1759.002
Degrees of freedom 32
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 862.334
Degrees of freedom 21
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.000
Tucker-Lewis Index (TLI) -0.347
Robust Comparative Fit Index (CFI) 0.000
Robust Tucker-Lewis Index (TLI) 0.093
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -8745.952
Loglikelihood unrestricted model (H1) -7866.451
Akaike (AIC) 17497.903
Bayesian (BIC) 17512.415
Sample-size adjusted Bayesian (SABIC) 17502.888
Root Mean Square Error of Approximation:
RMSEA 0.241
90 Percent confidence interval - lower 0.231
90 Percent confidence interval - upper 0.250
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 1.000
Robust RMSEA 0.467
90 Percent confidence interval - lower 0.402
90 Percent confidence interval - upper 0.534
P-value H_0: Robust RMSEA <= 0.050 0.000
P-value H_0: Robust RMSEA >= 0.080 1.000
Standardized Root Mean Square Residual:
SRMR 0.480
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
eta_1 =~
math2 1.000 6.850 0.536
math3 1.000 6.850 0.536
math4 1.000 6.850 0.536
math5 1.000 6.850 0.536
math6 1.000 6.850 0.536
math7 1.000 6.850 0.536
math8 1.000 6.850 0.536
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
eta_1 45.915 0.324 141.721 0.000 6.703 6.703
.math2 0.000 0.000 0.000
.math3 0.000 0.000 0.000
.math4 0.000 0.000 0.000
.math5 0.000 0.000 0.000
.math6 0.000 0.000 0.000
.math7 0.000 0.000 0.000
.math8 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
eta_1 46.917 4.832 9.709 0.000 1.000 1.000
.math2 (thet) 116.682 4.548 25.656 0.000 116.682 0.713
.math3 (thet) 116.682 4.548 25.656 0.000 116.682 0.713
.math4 (thet) 116.682 4.548 25.656 0.000 116.682 0.713
.math5 (thet) 116.682 4.548 25.656 0.000 116.682 0.713
.math6 (thet) 116.682 4.548 25.656 0.000 116.682 0.713
.math7 (thet) 116.682 4.548 25.656 0.000 116.682 0.713
.math8 (thet) 116.682 4.548 25.656 0.000 116.682 0.713
Generiamo il diagramma di percorso.
semPaths(ng_math_lavaan_fit, what = "path", whatLabels = "par")
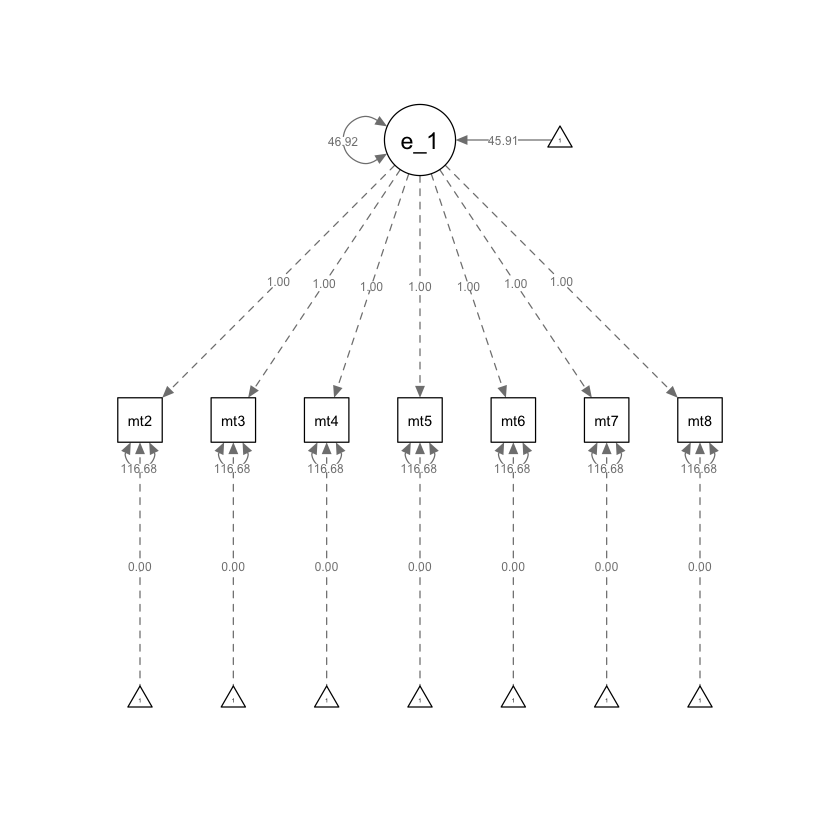
Calcoliamo le traiettorie predette.
#obtaining predicted factor scores for individuals
nlsy_math_predicted <- as.data.frame(cbind(nlsy_math_wide$id,lavPredict(ng_math_lavaan_fit)))
#naming columns
names(nlsy_math_predicted) <- c("id", "eta_1")
#looking at data
head(nlsy_math_predicted)
| id | eta_1 | |
|---|---|---|
| <dbl> | <dbl> | |
| 1 | 201 | 46.17558 |
| 2 | 303 | 38.59816 |
| 3 | 2702 | 56.16725 |
| 4 | 4303 | 47.51278 |
| 5 | 5002 | 51.06429 |
| 6 | 5005 | 49.05038 |
# calculating implied manifest scores
nlsy_math_predicted$math2 <- 1 * nlsy_math_predicted$eta_1
nlsy_math_predicted$math3 <- 1 * nlsy_math_predicted$eta_1
nlsy_math_predicted$math4 <- 1 * nlsy_math_predicted$eta_1
nlsy_math_predicted$math5 <- 1 * nlsy_math_predicted$eta_1
nlsy_math_predicted$math6 <- 1 * nlsy_math_predicted$eta_1
nlsy_math_predicted$math7 <- 1 * nlsy_math_predicted$eta_1
nlsy_math_predicted$math8 <- 1 * nlsy_math_predicted$eta_1
# reshaping wide to long
nlsy_math_predicted_long <- reshape(
data = nlsy_math_predicted,
timevar = c("grade"),
idvar = "id",
varying = c(
"math2", "math3", "math4",
"math5", "math6", "math7", "math8"
),
direction = "long", sep = ""
)
# sorting for easy viewing
# order by id and time
nlsy_math_predicted_long <- nlsy_math_predicted_long[order(nlsy_math_predicted_long$id, nlsy_math_predicted_long$grade), ]
# intraindividual change trajetories
ggplot(
data = nlsy_math_predicted_long, # data set
aes(x = grade, y = math, group = id)
) + # setting variables
# geom_point(size=.5) + #adding points to plot
geom_line(alpha = 0.1) + # adding lines to plot
# setting the x-axis with breaks and labels
scale_x_continuous(
limits = c(2, 8),
breaks = c(2, 3, 4, 5, 6, 7, 8),
name = "Grade at Testing"
) +
# setting the y-axis with limits breaks and labels
scale_y_continuous(
limits = c(10, 90),
breaks = c(10, 30, 50, 70, 90),
name = "Predicted PIAT Mathematics"
)
Warning message:
“Removed 7 rows containing missing values (`geom_line()`).”
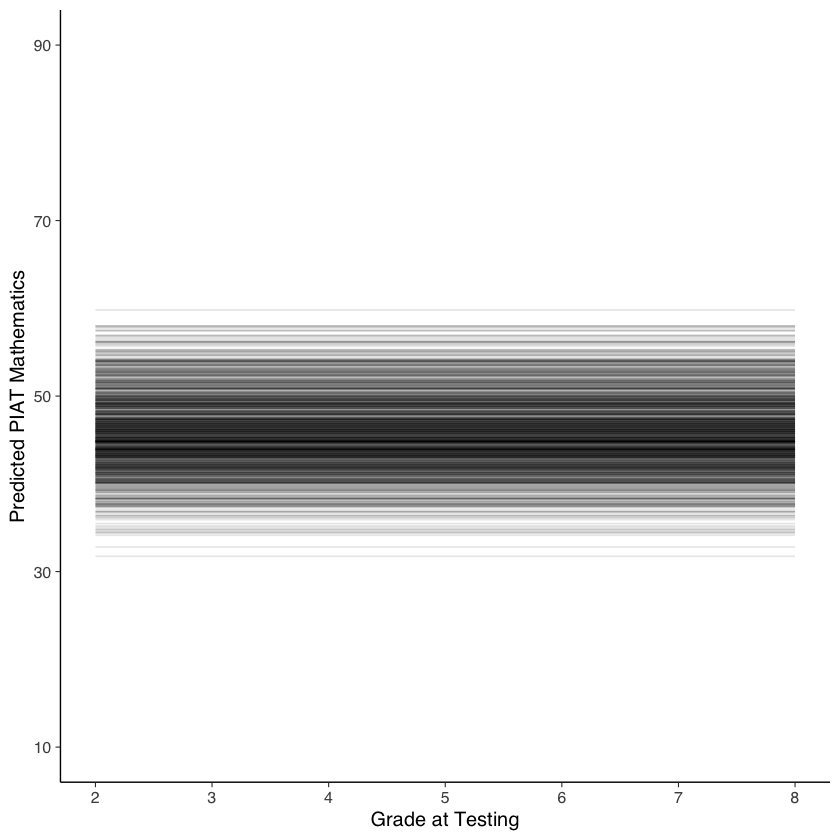
Come si può notare dal grafico, il modello che abbiamo utilizzato produce una serie di linee orizzontali, ciascuna rappresentante la traiettoria di crescita piatta dell’abilità matematica per ogni individuo. L’intercetta di queste traiettorie rappresenta il valore vero dell’abilità matematica di ciascun bambino, e tale valore rimane costante nel tempo.
31.3. Modello di crescita lineare#
Nella discussione dei modelli di crescita, il modello di assenza di crescita viene sempre seguito dall’esame del modello di crescita lineare. Infatti, i modelli di crescita lineare rappresentano spesso il punto di partenza quando si cerca di comprendere il cambiamento all’interno dell’individuo. Successivamente, possono essere considerati anche modelli di crescita non lineare.
Per questo motivo, procediamo ora all’implementazione di un modello di crescita latente lineare.
lg_math_lavaan_model <- '
# latent variable definitions
#intercept (note intercept is a reserved term)
eta_1 =~ 1*math2
eta_1 =~ 1*math3
eta_1 =~ 1*math4
eta_1 =~ 1*math5
eta_1 =~ 1*math6
eta_1 =~ 1*math7
eta_1 =~ 1*math8
#linear slope
eta_2 =~ 0*math2
eta_2 =~ 1*math3
eta_2 =~ 2*math4
eta_2 =~ 3*math5
eta_2 =~ 4*math6
eta_2 =~ 5*math7
eta_2 =~ 6*math8
# factor variances
eta_1 ~~ eta_1
eta_2 ~~ eta_2
# covariances among factors
eta_1 ~~ eta_2
# factor means
eta_1 ~ 1
eta_2 ~ 1
# manifest variances (made equivalent by naming theta)
math2 ~~ theta*math2
math3 ~~ theta*math3
math4 ~~ theta*math4
math5 ~~ theta*math5
math6 ~~ theta*math6
math7 ~~ theta*math7
math8 ~~ theta*math8
# manifest means (fixed at zero)
math2 ~ 0*1
math3 ~ 0*1
math4 ~ 0*1
math5 ~ 0*1
math6 ~ 0*1
math7 ~ 0*1
math8 ~ 0*1
' #end of model definition
Adattiamo il modello ai dati.
lg_math_lavaan_fit <- sem(lg_math_lavaan_model,
data = nlsy_math_wide,
meanstructure = TRUE,
estimator = "ML",
missing = "fiml"
)
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING: some cases are empty and will be ignored:
741”
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING:
due to missing values, some pairwise combinations have less than
10% coverage; use lavInspect(fit, "coverage") to investigate.”
Warning message in lav_mvnorm_missing_h1_estimate_moments(Y = X[[g]], wt = WT[[g]], :
“lavaan WARNING:
Maximum number of iterations reached when computing the sample
moments using EM; use the em.h1.iter.max= argument to increase the
number of iterations”
Esaminiamo il risultato ottenuto.
summary(lg_math_lavaan_fit, fit.measures = TRUE, standardized = TRUE) |>
print()
lavaan 0.6.15 ended normally after 38 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 12
Number of equality constraints 6
Used Total
Number of observations 932 933
Number of missing patterns 60
Model Test User Model:
Test statistic 204.484
Degrees of freedom 29
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 862.334
Degrees of freedom 21
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.791
Tucker-Lewis Index (TLI) 0.849
Robust Comparative Fit Index (CFI) 0.896
Robust Tucker-Lewis Index (TLI) 0.925
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -7968.693
Loglikelihood unrestricted model (H1) -7866.451
Akaike (AIC) 15949.386
Bayesian (BIC) 15978.410
Sample-size adjusted Bayesian (SABIC) 15959.354
Root Mean Square Error of Approximation:
RMSEA 0.081
90 Percent confidence interval - lower 0.070
90 Percent confidence interval - upper 0.091
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 0.550
Robust RMSEA 0.134
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.233
P-value H_0: Robust RMSEA <= 0.050 0.136
P-value H_0: Robust RMSEA >= 0.080 0.792
Standardized Root Mean Square Residual:
SRMR 0.121
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
eta_1 =~
math2 1.000 8.035 0.800
math3 1.000 8.035 0.799
math4 1.000 8.035 0.792
math5 1.000 8.035 0.779
math6 1.000 8.035 0.762
math7 1.000 8.035 0.742
math8 1.000 8.035 0.719
eta_2 =~
math2 0.000 0.000 0.000
math3 1.000 0.856 0.085
math4 2.000 1.712 0.169
math5 3.000 2.568 0.249
math6 4.000 3.424 0.325
math7 5.000 4.279 0.395
math8 6.000 5.135 0.459
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
eta_1 ~~
eta_2 -0.181 1.150 -0.158 0.875 -0.026 -0.026
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
eta_1 35.267 0.355 99.229 0.000 4.389 4.389
eta_2 4.339 0.088 49.136 0.000 5.070 5.070
.math2 0.000 0.000 0.000
.math3 0.000 0.000 0.000
.math4 0.000 0.000 0.000
.math5 0.000 0.000 0.000
.math6 0.000 0.000 0.000
.math7 0.000 0.000 0.000
.math8 0.000 0.000 0.000
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
eta_1 64.562 5.659 11.408 0.000 1.000 1.000
eta_2 0.733 0.327 2.238 0.025 1.000 1.000
.math2 (thet) 36.230 1.867 19.410 0.000 36.230 0.359
.math3 (thet) 36.230 1.867 19.410 0.000 36.230 0.358
.math4 (thet) 36.230 1.867 19.410 0.000 36.230 0.352
.math5 (thet) 36.230 1.867 19.410 0.000 36.230 0.341
.math6 (thet) 36.230 1.867 19.410 0.000 36.230 0.326
.math7 (thet) 36.230 1.867 19.410 0.000 36.230 0.309
.math8 (thet) 36.230 1.867 19.410 0.000 36.230 0.290
Generiamo un diagramma di percorso.
semPaths(lg_math_lavaan_fit,what = "path", whatLabels = "par")
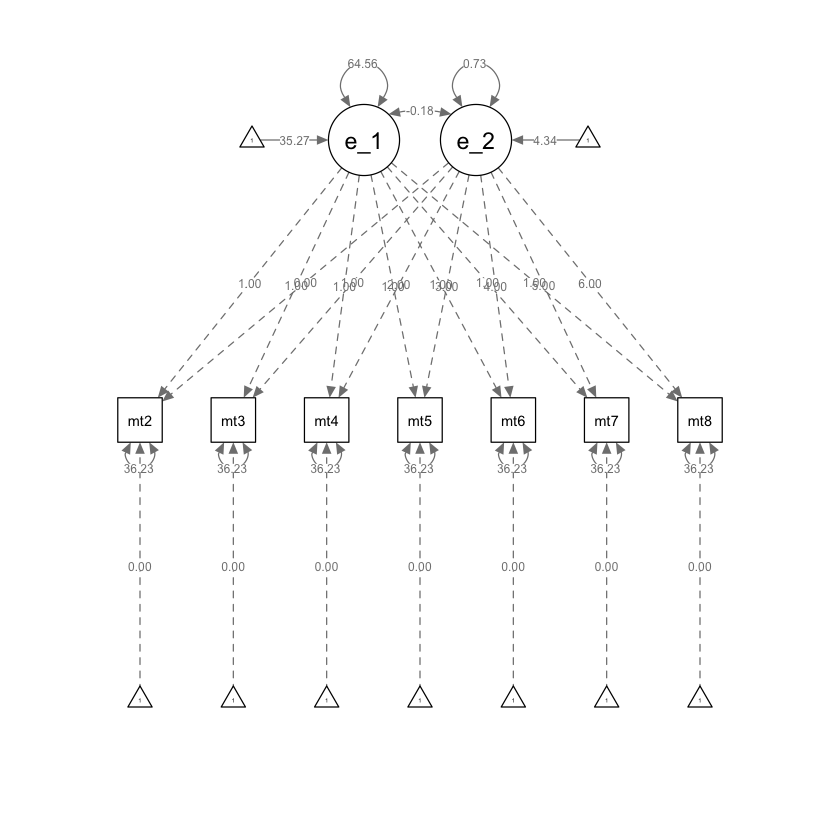
Esaminiamo le traiettorie di crescita.
nlsy_math_predicted <- as.data.frame(
cbind(nlsy_math_wide$id, lavPredict(lg_math_lavaan_fit))
)
#naming columns
names(nlsy_math_predicted) <- c("id", "eta_1", "eta_2")
head(nlsy_math_predicted)
| id | eta_1 | eta_2 | |
|---|---|---|---|
| <dbl> | <dbl> | <dbl> | |
| 1 | 201 | 36.94675 | 4.534084 |
| 2 | 303 | 26.03589 | 4.050780 |
| 3 | 2702 | 49.70187 | 4.594149 |
| 4 | 4303 | 41.04200 | 4.548064 |
| 5 | 5002 | 37.01240 | 4.496746 |
| 6 | 5005 | 37.68809 | 4.324198 |
#calculating implied manifest scores
nlsy_math_predicted$math2 <- 1 * nlsy_math_predicted$eta_1 + 0 * nlsy_math_predicted$eta_2
nlsy_math_predicted$math3 <- 1 * nlsy_math_predicted$eta_1 + 1 * nlsy_math_predicted$eta_2
nlsy_math_predicted$math4 <- 1 * nlsy_math_predicted$eta_1 + 2 * nlsy_math_predicted$eta_2
nlsy_math_predicted$math5 <- 1 * nlsy_math_predicted$eta_1 + 3 * nlsy_math_predicted$eta_2
nlsy_math_predicted$math6 <- 1 * nlsy_math_predicted$eta_1 + 4 * nlsy_math_predicted$eta_2
nlsy_math_predicted$math7 <- 1 * nlsy_math_predicted$eta_1 + 5 * nlsy_math_predicted$eta_2
nlsy_math_predicted$math8 <- 1 * nlsy_math_predicted$eta_1 + 6 * nlsy_math_predicted$eta_2
# reshaping wide to long
nlsy_math_predicted_long <- reshape(
data = nlsy_math_predicted,
timevar = c("grade"),
idvar = "id",
varying = c(
"math2", "math3", "math4", "math5", "math6", "math7", "math8"
),
direction = "long", sep = ""
)
head(nlsy_math_predicted_long)
| id | eta_1 | eta_2 | grade | math | |
|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | |
| 201.2 | 201 | 36.94675 | 4.534084 | 2 | 36.94675 |
| 303.2 | 303 | 26.03589 | 4.050780 | 2 | 26.03589 |
| 2702.2 | 2702 | 49.70187 | 4.594149 | 2 | 49.70187 |
| 4303.2 | 4303 | 41.04200 | 4.548064 | 2 | 41.04200 |
| 5002.2 | 5002 | 37.01240 | 4.496746 | 2 | 37.01240 |
| 5005.2 | 5005 | 37.68809 | 4.324198 | 2 | 37.68809 |
# sorting for easy viewing
# order by id and time
nlsy_math_predicted_long <-
nlsy_math_predicted_long[order(nlsy_math_predicted_long$id, nlsy_math_predicted_long$grade), ]
head(nlsy_math_predicted_long)
| id | eta_1 | eta_2 | grade | math | |
|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | |
| 201.2 | 201 | 36.94675 | 4.534084 | 2 | 36.94675 |
| 201.3 | 201 | 36.94675 | 4.534084 | 3 | 41.48083 |
| 201.4 | 201 | 36.94675 | 4.534084 | 4 | 46.01492 |
| 201.5 | 201 | 36.94675 | 4.534084 | 5 | 50.54900 |
| 201.6 | 201 | 36.94675 | 4.534084 | 6 | 55.08309 |
| 201.7 | 201 | 36.94675 | 4.534084 | 7 | 59.61717 |
ggplot(
data = nlsy_math_predicted_long, # data set
aes(x = grade, y = math, group = id)
) + # setting variables
# geom_point(size=.5) + #adding points to plot
geom_line(alpha = 0.15) + # adding lines to plot
# setting the x-axis with breaks and labels
scale_x_continuous(
limits = c(2, 8),
breaks = c(2, 3, 4, 5, 6, 7, 8),
name = "Grade at Testing"
) +
# setting the y-axis with limits breaks and labels
scale_y_continuous(
limits = c(10, 90),
breaks = c(10, 30, 50, 70, 90),
name = "Predicted PIAT Mathematics"
)
Warning message:
“Removed 7 rows containing missing values (`geom_line()`).”
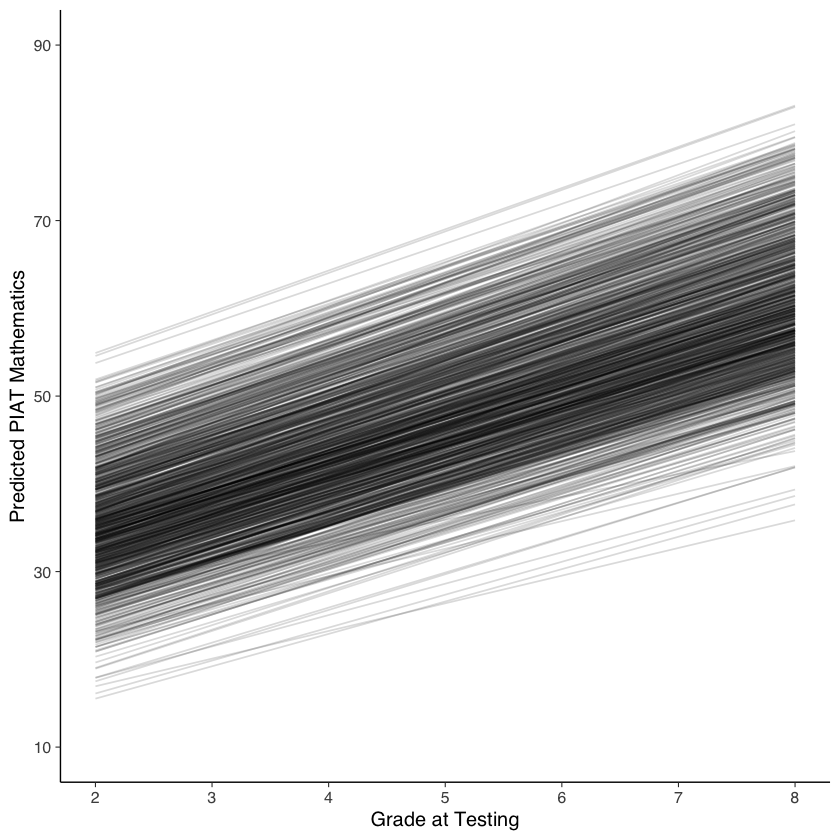
Il modello di crescita latente lineare rappresenta la traiettoria di ogni bambino come una linea retta, evidenziando le differenze tra le abilità matematiche individuali nel tempo. Come mostrato dal grafico, per tutti i bambini, l’abilità matematica “vera” aumenta di circa 5 punti per ogni anno scolastico.
31.3.1. Sintassi alternativa#
Per semplificare la scrittura del modello possiamo usare la funzione growth. Tuttavia, per il modello discusso in precedenza, è necessario specificare un parametro aggiuntivo rispetto ai default di growth: vogliamo che le varianze residue di math siano costanti nel tempo.
m1 <- '
i =~ 1*math2 + 1*math3 + 1*math4 + 1*math5 + 1*math6 + 1*math7 + 1*math8
s =~ 0 * math2 + 1 * math3 + 2 * math4 + 3 * math5 + 4 * math6 + 5 * math7 + 6 * math8
# manifest variances (made equivalent by naming theta)
math2 ~~ theta*math2
math3 ~~ theta*math3
math4 ~~ theta*math4
math5 ~~ theta*math5
math6 ~~ theta*math6
math7 ~~ theta*math7
math8 ~~ theta*math8
'
Adattiamo il modello.
fit_m1 <- growth(
m1,
data = nlsy_math_wide,
estimator = "ML",
missing = "fiml"
)
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING: some cases are empty and will be ignored:
741”
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING:
due to missing values, some pairwise combinations have less than
10% coverage; use lavInspect(fit, "coverage") to investigate.”
Warning message in lav_mvnorm_missing_h1_estimate_moments(Y = X[[g]], wt = WT[[g]], :
“lavaan WARNING:
Maximum number of iterations reached when computing the sample
moments using EM; use the em.h1.iter.max= argument to increase the
number of iterations”
Otteniamo lo stesso risultato trovato con sem.
print(fitMeasures(fit_m1, c("chisq", "df", "pvalue", "cfi", "rmsea")))
chisq df pvalue cfi rmsea
204.484 29.000 0.000 0.791 0.081
31.3.2. Interpretazione dei parametri#
Nell’output relativo ad Intercepts, il valore eta_1 uguale a 35.267 indica il valore predetto di matematica al tempo \(t_0\). Il parametro eta_2 specifica che, per ogni incremento di un’unità sulla metrica utilizzata del tempo, ci si aspetto che il valore predetto di matematica aumenti di 4.339 punti. Nell’output relativo ad Variances, il parametro eta_1 uguale a 64.562 indica la varianza delle intercette tra gli studenti; il parametro eta_2 uguale a 0.733 indica la varianza delle pendenze tra gli studenti. Prendendo la radice quadrata e assumendo la normalità, l’intervallo \(35.267 \pm 1.96 \sqrt(64.562)\) fornisce una stima dell’intervallo al 95% dei valori plausibili delle medie dei punteggi di matematica tra gli studenti – non l’intervallo di fiducia frequentista, in quanto l’intervallo è calcolato attorno alla stima del valore vero. In maniera corrispondente, l’intervallo \(4.339 \pm 1.96 \sqrt(0.733)\) fornisce una stima dell’intervallo al 95% dei valori plausibili delle pendenze dei punteggi di matematica tra gli studenti.
La covarianza stimata di -0.181 (SE = 1.150) indica che non vi è covarianza tra intercette e pendenze. Se l’effetto fosse positivo, potremmo dire che c’è una relazione positiva tra l’intercetta e la pendenza: più alto è il valore iniziale di matematica, più forte è la crescita dei punteggi di matematica nel tempo. Una covarianza negativa tra intercetta e pendenza implicherebbe che più alto è il punteggio iniziale di matematica, più debole è l’aumento dei puneggi di matematica nel tempo.
31.4. Confronto con il modello misto#
Effettueremo un’ulteriore analisi utilizzando un modello misto. Tuttavia, in questo caso non possiamo ottenere gli stessi risultati a causa dei dati mancanti. Per stimare i parametri del modello, abbiamo utilizzato la procedura di massima verosimiglianza (ML) e abbiamo gestito i dati mancanti utilizzando la procedura fiml in lavaan. Questo metodo non imputa dati mancanti, ma utilizza i dati disponibili di ogni caso per stimare i parametri di massima verosimiglianza. Tuttavia, nel caso dei modelli misti, la strategia FIML non è disponibile. Pertanto, elimineremo semplicemente tutti i casi con dati mancanti per procedere con l’analisi.
In formato long, i dati sono i seguenti.
nlsy_math_long |>
head()
| id | grade | math | |
|---|---|---|---|
| <int> | <dbl> | <int> | |
| 201.3 | 201 | 3 | 38 |
| 201.5 | 201 | 5 | 55 |
| 303.2 | 303 | 2 | 26 |
| 303.5 | 303 | 5 | 33 |
| 2702.2 | 2702 | 2 | 56 |
| 2702.4 | 2702 | 4 | 58 |
Sottraiamo 2 dalla variabile grade in modo che il valore 0 corrisponda alla prima rilevazione temporale. In questo modo, l’intercetta rappresenterà il valore atteso del punteggio di matematica per la prima rilevazione temporale (quando grade è pari a 2).
nlsy_math_long$grade_c2 <- nlsy_math_long$grade - 2
Il modello misto è adattato utilizzando la funzione lmer. È importante notare che il modello presenta un’intercetta casuale, il che significa che assume la stessa pendenza per ogni individuo (ovvero lo stesso tasso di crescita). Questo è in linea con quanto mostrato nella figura precedente, che illustra le traiettorie di crescita.
L’argomento REML = FALSE indica che stiamo utilizzando la stima di massima verosimiglianza invece della procedura predefinita. Inoltre, l’argomento na.action = na.exclude specifica che le osservazioni con dati mancanti saranno escluse.
fit_lmer <- lmer(
math ~ 1 + grade_c2 + (1 | id),
data = nlsy_math_long,
REML = FALSE,
na.action = na.exclude
)
summary(fit_lmer) |>
print()
Linear mixed model fit by maximum likelihood ['lmerMod']
Formula: math ~ 1 + grade_c2 + (1 | id)
Data: nlsy_math_long
AIC BIC logLik deviance df.resid
15957.7 15980.5 -7974.8 15949.7 2217
Scaled residuals:
Min 1Q Median 3Q Max
-3.2082 -0.5265 0.0081 0.5456 2.5651
Random effects:
Groups Name Variance Std.Dev.
id (Intercept) 67.30 8.204
Residual 39.31 6.270
Number of obs: 2221, groups: id, 932
Fixed effects:
Estimate Std. Error t value
(Intercept) 35.33081 0.36264 97.43
grade_c2 4.29352 0.08266 51.94
Correlation of Fixed Effects:
(Intr)
grade_c2 -0.555
Dall’output vediamo che il punteggio di matematica in corrispondenza del secondo grado scolastico (codificato qui con 0) è uguale a 35.33 (0.36). Il tasso di crescita, ovvero l’aumento atteso dei punteggi di matematica per ciascun grado scolastico è uguale a 4.29 (0.08).
Una rappresentazione grafica dei punteggi predetti dal modello misto può essere ottenuta nel modo seguente.
gr <- emmeans::ref_grid(fit_lmer, cov.keep= c('grade_c2'))
emm <- emmeans(gr, spec= c('grade_c2'), level= 0.95)
nlsy_math_long |>
ggplot(aes(x= grade_c2, y= math)) +
geom_ribbon(
data= data.frame(emm),
aes(ymin= lower.CL, ymax= upper.CL, y= NULL), fill= 'grey80'
) +
geom_line(data= data.frame(emm), aes(y= emmean)) +
geom_point()
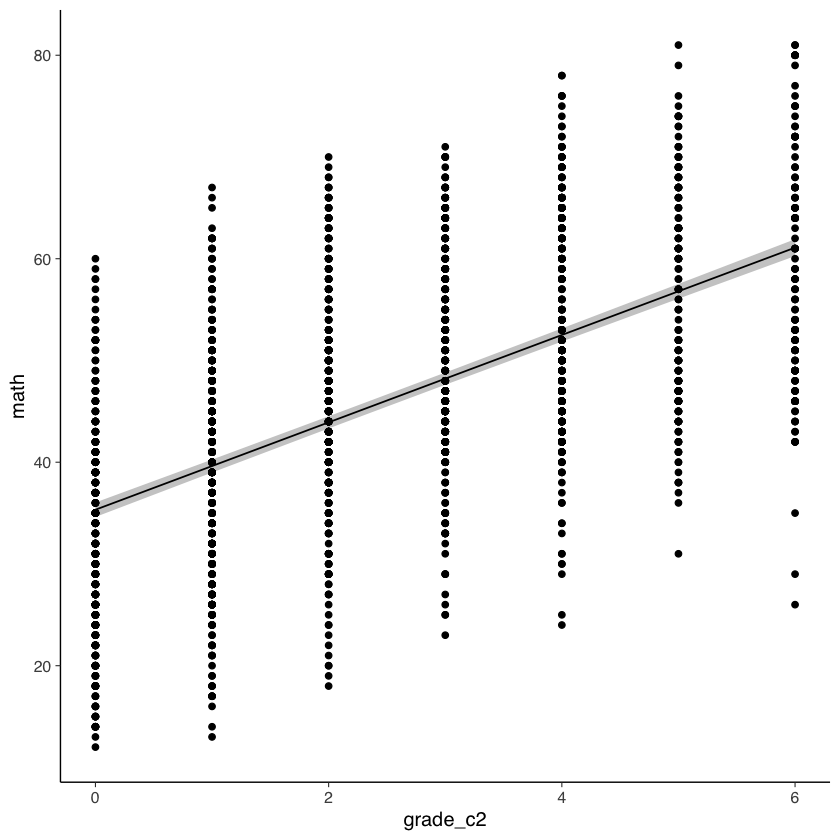
Questi risultati, ottenuti escludendo tutte le osservazioni con dati mancanti, sono molto simili ai risultati ottenuti usando lavaan (si veda la figura con le traiettorie di crescita del modello LGM).
31.5. Crescita non lineare#
È possibile verificare se il cambiamento ha una forma non lineare. Il metodo utilizzato per costruire questo modello è simile all’aggiunta di variabili dummy in un modello di regressione. Tuttavia, è necessario modificare i carichi fattoriali per la variabile latente del pendio in modo che solo il primo e l’ultimo carico fattoriale siano fissati rispettivamente a 0 e 1, mentre i restanti carichi fattoriali saranno liberamente stimati. In questo modo, la pendenza rappresenterà l’ammontare totale del cambiamento dall’inizio alla fine dell’intervallo di tempo. I nuovi carichi fattoriali stimati rappresenteranno la proporzione di cambiamento avvenuto dall’inizio fino a quel punto rispetto al cambiamento totale osservato.
mod_nl <- "
i =~ 1*math2 + 1*math3 + 1*math4 + 1*math5 + 1*math6 + 1*math7 + 1*math8
s = ~ 0 * math2 + math3 + math4 + math5 + math6 + math7 + 1*math8
math2 ~~ theta*math2
math3 ~~ theta*math3
math4 ~~ theta*math4
math5 ~~ theta*math5
math6 ~~ theta*math6
math7 ~~ theta*math7
math8 ~~ theta*math8
"
Adattiamo il modello ai dati.
fit_nl <- growth(
mod_nl,
data = nlsy_math_wide,
estimator = "ML",
missing = "fiml")
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING: some cases are empty and will be ignored:
741”
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING:
due to missing values, some pairwise combinations have less than
10% coverage; use lavInspect(fit, "coverage") to investigate.”
Warning message in lav_mvnorm_missing_h1_estimate_moments(Y = X[[g]], wt = WT[[g]], :
“lavaan WARNING:
Maximum number of iterations reached when computing the sample
moments using EM; use the em.h1.iter.max= argument to increase the
number of iterations”
Esaminiamo la soluzione.
summary(fit_nl, fit.measures = TRUE, standardized = TRUE) |>
print()
lavaan 0.6.15 ended normally after 100 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 17
Number of equality constraints 6
Used Total
Number of observations 932 933
Number of missing patterns 60
Model Test User Model:
Test statistic 52.947
Degrees of freedom 24
P-value (Chi-square) 0.001
Model Test Baseline Model:
Test statistic 862.334
Degrees of freedom 21
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.966
Tucker-Lewis Index (TLI) 0.970
Robust Comparative Fit Index (CFI) 1.000
Robust Tucker-Lewis Index (TLI) 1.023
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -7892.924
Loglikelihood unrestricted model (H1) -7866.451
Akaike (AIC) 15807.848
Bayesian (BIC) 15861.059
Sample-size adjusted Bayesian (SABIC) 15826.124
Root Mean Square Error of Approximation:
RMSEA 0.036
90 Percent confidence interval - lower 0.023
90 Percent confidence interval - upper 0.049
P-value H_0: RMSEA <= 0.050 0.961
P-value H_0: RMSEA >= 0.080 0.000
Robust RMSEA 0.000
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.177
P-value H_0: Robust RMSEA <= 0.050 0.644
P-value H_0: Robust RMSEA >= 0.080 0.284
Standardized Root Mean Square Residual:
SRMR 0.094
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
i =~
math2 1.000 8.509 0.839
math3 1.000 8.509 0.857
math4 1.000 8.509 0.851
math5 1.000 8.509 0.840
math6 1.000 8.509 0.823
math7 1.000 8.509 0.808
math8 1.000 8.509 0.791
s =~
math2 0.000 0.000 0.000
math3 0.295 0.019 15.783 0.000 1.849 0.186
math4 0.533 0.019 28.588 0.000 3.346 0.335
math5 0.664 0.021 31.083 0.000 4.167 0.411
math6 0.799 0.022 36.470 0.000 5.016 0.485
math7 0.901 0.030 30.314 0.000 5.656 0.537
math8 1.000 6.276 0.583
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
i ~~
s -13.303 7.281 -1.827 0.068 -0.249 -0.249
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.math2 0.000 0.000 0.000
.math3 0.000 0.000 0.000
.math4 0.000 0.000 0.000
.math5 0.000 0.000 0.000
.math6 0.000 0.000 0.000
.math7 0.000 0.000 0.000
.math8 0.000 0.000 0.000
i 32.400 0.474 68.399 0.000 3.808 3.808
s 25.539 0.731 34.916 0.000 4.070 4.070
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.math2 (thet) 30.502 1.678 18.182 0.000 30.502 0.296
.math3 (thet) 30.502 1.678 18.182 0.000 30.502 0.310
.math4 (thet) 30.502 1.678 18.182 0.000 30.502 0.305
.math5 (thet) 30.502 1.678 18.182 0.000 30.502 0.297
.math6 (thet) 30.502 1.678 18.182 0.000 30.502 0.286
.math7 (thet) 30.502 1.678 18.182 0.000 30.502 0.275
.math8 (thet) 30.502 1.678 18.182 0.000 30.502 0.264
i 72.408 6.590 10.988 0.000 1.000 1.000
s 39.385 11.371 3.464 0.001 1.000 1.000
Effettuiamo un test del rapporto di verosimiglianza per confrontare il modello di crescita lineare con quello che assume una crescita non lineare.
lavTestLRT(fit_m1, fit_nl) |>
print()
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
fit_nl 24 15808 15861 52.947
fit_m1 29 15949 15978 204.484 151.54 0.17733 5 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
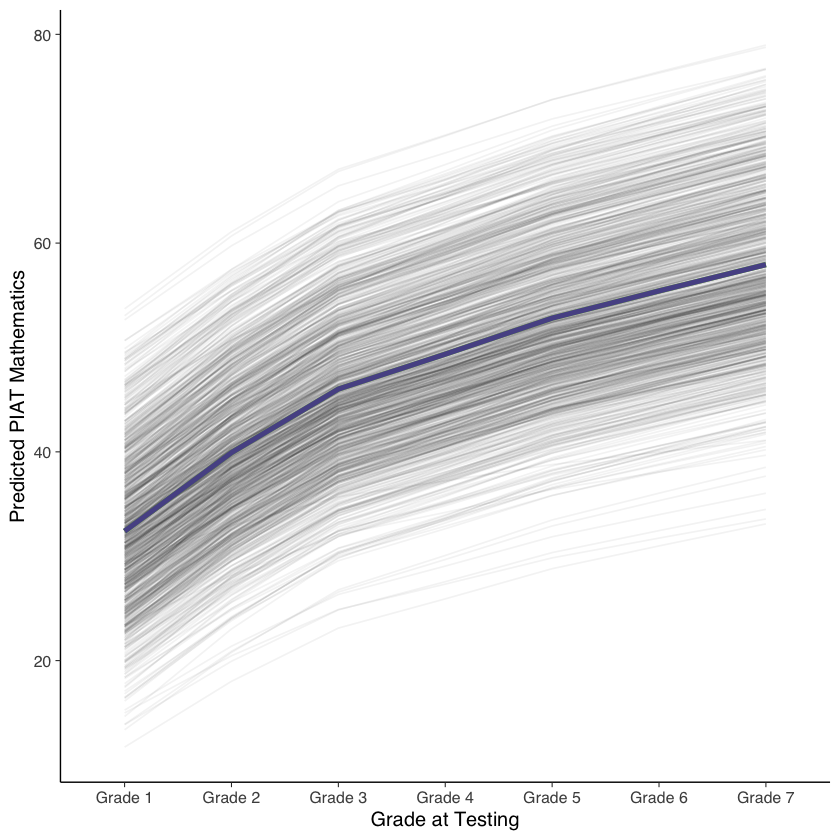
Il risultato indica che il cambiamento è non lineare. Possiamo visualizzare il cambiamento nel modo seguente.
# extract just th eloadings of the slopes
loadings <- parameterestimates(fit_nl) %>% # get estimates
filter(lhs == "s", op == "=~") %>% # filter the rows we want
.[["est"]] # extract "est" variable
# print result
print(loadings)
[1] 0.0000000 0.2946469 0.5331543 0.6640286 0.7992432 0.9012768 1.0000000
# predict scores
pred_lgm3 <- predict(fit_nl)
# create long data for each individual
pred_lgm3_long <- map(loadings, # loop over time
function(x) pred_lgm3[, 1] +
x * pred_lgm3[, 2]) %>%
reduce(cbind) %>% # bring together the wave predictions
as.data.frame()
# predict scores
pred_lgm3 <- predict(fit_nl)
# create long data for each individual
pred_lgm3_long <- map(loadings, # loop over time
function(x) pred_lgm3[, 1] +
x * pred_lgm3[, 2]) %>%
reduce(cbind) %>% # bring together the wave predictions
as.data.frame() %>% # make data frame
setNames(str_c("Grade ", 1:7)) %>% # give names to variables
mutate(id = row_number()) %>% # make unique id
gather(-id, key = grade, value = pred) # make long format
pred_lgm3_long %>%
ggplot(aes(grade, pred, group = id)) + # what variables to plot?
geom_line(alpha = 0.05) + # add a transparent line for each person
stat_summary( # add average line
aes(group = 1),
fun = mean,
geom = "line",
size = 1.5,
color = "green"
) +
stat_summary(data = pred_lgm3_long, # add average from linear model
aes(group = 1),
fun = mean,
geom = "line",
size = 1.5,
color = "red",
alpha = 0.5
) +
stat_summary(data = pred_lgm3_long, # add average from squared model
aes(group = 1),
fun = mean,
geom = "line",
size = 1.5,
color = "blue",
alpha = 0.5
) +
labs(y = "Predicted PIAT Mathematics", # labels
x = "Grade at Testing")
Warning message:
“Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.”
Warning message:
“Removed 7 rows containing non-finite values (`stat_summary()`).”
Warning message:
“Removed 7 rows containing non-finite values (`stat_summary()`).”
Warning message:
“Removed 7 rows containing non-finite values (`stat_summary()`).”
Warning message:
“Removed 7 rows containing missing values (`geom_line()`).”
31.6. Considerazioni conclusive#
Questo tutorial ha illustrato come impostare e adattare modelli di crescita lineare nel framework di modellizzazione SEM utilizzando il pacchetto lavaan in R, nonché come calcolare e rappresentare graficamente le traiettorie di crescita previste dal modello.
I modelli di crescita lineare sono un punto di partenza per studiare il cambiamento individuale. Tuttavia, non sempre catturano bene il processo di cambiamento. Pertanto, è utile confrontare modelli aggiuntivi e considerare le differenze di gruppo. L’adattamento dei modelli di crescita nei framework di modellizzazione multilivello e delle equazioni strutturali ha vantaggi e limitazioni. Ad esempio, il framework delle equazioni strutturali fornisce indici di adattamento globale come RMSEA, CFI e TLI, mentre l’approccio dei modelli misti può usare solo AIC e BIC e le diagnostiche del modello come il grafico dei residui.”
Quando si adattano i modelli di crescita lineare, è importante considerare la metrica del tempo. Nel nostro esempio, abbiamo usato il grado scolastico come metrica temporale, ma altre metriche sono possibili. Ad esempio, l’età al momento del test potrebbe essere più rilevante perché cattura meglio la distanza tra le rilevazioni. Inoltre, ci possono essere limitazioni nell’utilizzo del grado scolastico, come nel caso di studenti che ripetono o saltano un anno.
L’intercetta può essere posizionata in qualsiasi punto temporale. Nel nostro esempio, l’abbiamo centrata sulla valutazione della seconda elementare perché era la prima misurazione disponibile. Tuttavia, è importante scegliere un punto di origine significativo per lo studio. Ad esempio, centrare l’intercetta alla fine dell’ottava elementare potrebbe essere importante per valutare la preparazione per la scuola superiore.
