36. Invarianza di misurazione#
In questo capitolo, esaminiamo come il modello a fattore comune possa essere utilizzato per studiare i cambiamenti nei fattori comuni attraverso l’uso di modelli di crescita latente. Ci concentriamo sui fattori comuni misurati da variabili osservate con punteggio continuo.
Un concetto chiave è stabilire una metrica comune per le variabili latenti nel tempo. A differenza delle variabili osservate, le variabili latenti non hanno una scala intrinseca e longitudinalmente è necessario che quella scala sia la stessa nel tempo. Questo viene fatto testando l’invarianza fattoriale.
In questo tutorial, introduciamo il test di invarianza di misura nel contesto di un modello a fattore longitudinale e come un modello di crescita latente di secondo ordine possa essere utilizzato per descrivere il cambiamento in un fattore latente. Questo tutorial segue l’esempio fornito nel Capitolo 14 Grimm et al. [GRE16]. Utilizzando dati con tre misurazioni temporali succesive dall’ECLS-K, testiamo l’invarianza fattoriale e quindi utilizziamo un modello di crescita di secondo ordine per descrivere il cambiamento nei punteggi del fattore nel tempo.
36.1. Invarianza fattoriale longitudinale#
L’invarianza fattoriale longitudinale si riferisce all’equivalenza di alcuni parametri del modello a fattore comune nel tempo. Avere una struttura fattoriale invariante è importante per l’utilizzo dell’analisi fattoriale come strumento di indagine scientifica. I fattori non hanno un’unità di misura o un significato intrinseco e la loro interpretazione deriva dalle loro relazioni con le variabili osservate. Se un fattore deve essere trattato come lo stesso in diverse occasioni temporali di misurazione, l’associazione di quel fattore con altre variabili deve rimanere costante nel tempo.
Il test di invarianza fattoriale è una procedura multi-step che comporta l’adattamento di quattro modelli con un numero crescente di vincoli: il modello di invarianza configurale, il modello di invarianza debole, il modello di invarianza forte e il modello di invarianza rigorosa.
Il modello di invarianza configurale richiede che il numero di fattori e la struttura delle saturazioni fattoriali siano uguali nelle diverse occasioni di misurazione. Altre caratteristiche come le varianze e le medie dei fattori possono variare. I fattori estratti in ogni occasione possono essere interpretati in modo simile, ma non possono essere considerati come misure di costrutti identici o sulla stessa scala.
I modelli di invarianza configurale sono usati come punto di partenza per confrontare altri modelli con vincoli maggiori. Questi modelli presuppongono che lo stesso numero di fattori sia presente in ogni occasione di misurazione, ma questa ipotesi potrebbe non essere vera. I ricercatori dovrebbero verificare che le ipotesi dell’invarianza configurale siano soddisfatte prima di procedere con i successivi test di invarianza.
L’invarianza fattoriale debole è il modello meno vincolato tra i tre modelli di invarianza metrica descritti da Meredith (1993). Questo modello richiede che la matrice delle saturazioni fattoriali sia uguale in tutte le rilevazioni temporali, ma non impone altre restrizioni. Poiché la matrice delle saturazioni fattoriali definisce le covarianze tra le variabili osservate, l’invarianza fattoriale debole crea strutture di covarianza proporzionali nel tempo.
L’invarianza forte fornisce un livello più elevato di invarianza di misura vincolando le intercette delle variabili osservate ad essere uguali nelle diverse occasioni di misurazione e consentendo al contempo al vettore delle medie delle variabili latenti di variare nel tempo. Ciò significa che tutti i cambiamenti longitudinali nelle medie delle variabili osservate sono spiegati dal fattore(i) comune(i).
L’invarianza fattoriale rigorosa è il modello di fattore longitudinale con i vincoli più forti. Oltre ai vincoli sulle saturazioni fattoriali e sulle intercette delle variabili osservate, questo modello richiede che le varianze uniche siano uguali nelle diverse occasioni di misurazione. In questo modello, tutti i cambiamenti longitudinali nelle medie osservate, nelle varianze e nelle covarianze sono attribuiti ai cambiamenti nei fattori comuni nel tempo.
36.2. Un esempio concreto#
Questo tutorial segue l’esempio del Capitolo 14 di Grimm et al. [GRE16]. Utilizzando dati relativi a 3 misurazioni dell’ECLS-K, testiamo l’invarianza fattoriale e poi usiamo un modello di crescita latente di secondo ordine per descrivere il cambiamento nei punteggi fattoriali nel tempo.
Carichiamo i pacchetti necessari.
Leggiamo i dati.
filepath <- "https://raw.githubusercontent.com/LRI-2/Data/main/GrowthModeling/ECLS_Science.dat"
# read in the text data file using the url() function
dat <- read.table(file = url(filepath), na.strings = ".")
names(dat) <- c(
"id", "s_g3", "r_g3", "m_g3", "s_g5", "r_g5", "m_g5", "s_g8",
"r_g8", "m_g8", "st_g3", "rt_g3", "mt_g3", "st_g5", "rt_g5",
"mt_g5", "st_g8", "rt_g8", "mt_g8"
)
# selecting only the variables of interest
dat <- dat[, c(
"id", "s_g3", "r_g3", "m_g3", "s_g5", "r_g5", "m_g5", "s_g8",
"r_g8", "m_g8"
)]
head(dat, 10)
| id | s_g3 | r_g3 | m_g3 | s_g5 | r_g5 | m_g5 | s_g8 | r_g8 | m_g8 | |
|---|---|---|---|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | |
| 1 | 1 | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| 2 | 3 | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| 3 | 8 | NA | NA | NA | NA | NA | NA | 103.90 | 204.10 | 166.67 |
| 4 | 16 | 51.57 | 142.18 | 115.59 | 65.94 | 141.02 | 133.67 | 86.90 | 169.83 | 156.67 |
| 5 | 28 | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| 6 | 44 | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| 7 | 46 | 72.09 | 154.43 | 96.87 | 79.44 | 170.57 | 116.28 | 89.08 | 192.07 | 132.40 |
| 8 | 62 | 34.71 | 106.40 | 87.86 | 47.44 | 145.72 | 104.68 | NA | NA | NA |
| 9 | 66 | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| 10 | 74 | 62.94 | 126.06 | 92.47 | 73.70 | 145.17 | 124.73 | 92.67 | 193.43 | 133.93 |
Otteniamo le statistiche descrittive.
psych::describe(dat[, -1]) |>
print()
vars n mean sd median trimmed mad min max range skew
s_g3 1 1442 50.99 15.62 50.94 50.82 16.76 18.37 92.66 74.29 0.08
r_g3 2 1430 127.66 29.22 126.97 128.44 31.33 51.46 195.82 144.36 -0.21
m_g3 3 1442 99.72 25.54 102.60 99.99 27.71 35.72 159.40 123.68 -0.10
s_g5 4 1135 65.25 16.18 67.53 65.99 16.52 22.57 103.23 80.66 -0.39
r_g5 5 1133 151.09 27.31 152.33 153.10 26.73 64.69 202.22 137.53 -0.62
m_g5 6 1136 124.35 25.17 128.64 126.08 25.14 50.87 169.53 118.66 -0.58
s_g8 7 947 84.89 16.71 88.93 86.88 14.81 29.61 107.90 78.29 -0.99
r_g8 8 941 172.05 27.73 179.70 175.54 24.91 89.15 208.44 119.29 -0.98
m_g8 9 945 142.47 22.50 147.36 145.07 21.23 67.75 172.20 104.45 -0.94
kurtosis se
s_g3 -0.59 0.41
r_g3 -0.50 0.77
m_g3 -0.70 0.67
s_g5 -0.49 0.48
r_g5 -0.04 0.81
m_g5 -0.24 0.75
s_g8 0.48 0.54
r_g8 0.24 0.90
m_g8 0.36 0.73
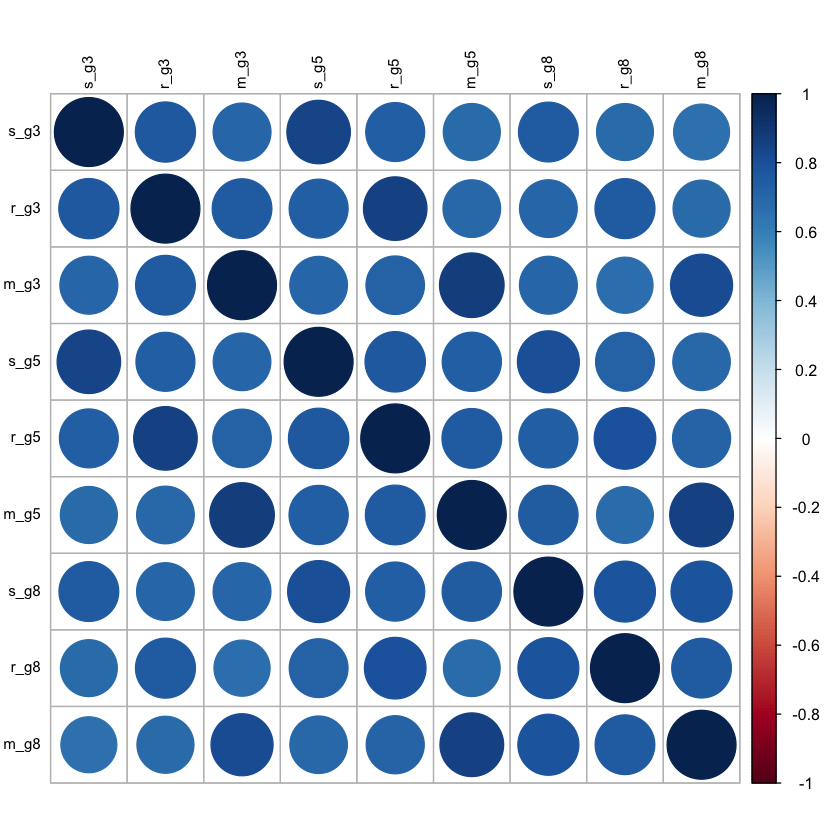
Calcoliamo le correlazioni.
round(cor(dat[, -1], use = "pairwise.complete"), 2) |>
print()
s_g3 r_g3 m_g3 s_g5 r_g5 m_g5 s_g8 r_g8 m_g8
s_g3 1.00 0.76 0.71 0.85 0.73 0.68 0.75 0.68 0.66
r_g3 0.76 1.00 0.75 0.73 0.85 0.70 0.70 0.76 0.68
m_g3 0.71 0.75 1.00 0.70 0.72 0.88 0.71 0.66 0.81
s_g5 0.85 0.73 0.70 1.00 0.77 0.74 0.81 0.73 0.70
r_g5 0.73 0.85 0.72 0.77 1.00 0.75 0.74 0.80 0.71
m_g5 0.68 0.70 0.88 0.74 0.75 1.00 0.74 0.68 0.85
s_g8 0.75 0.70 0.71 0.81 0.74 0.74 1.00 0.78 0.78
r_g8 0.68 0.76 0.66 0.73 0.80 0.68 0.78 1.00 0.75
m_g8 0.66 0.68 0.81 0.70 0.71 0.85 0.78 0.75 1.00
corrplot(cor(dat[, -1], use = "pairwise.complete"), order = "original", tl.col = "black", tl.cex = .75)
36.2.1. Modello di invarianza configurale#
Il modello di invarianza configurale impone pochi vincoli sulla struttura del fattore nel tempo. L’unico vincolo è che il numero di fattori e la struttura delle saturazioni fattoriali siano uguali nelle diverse occasioni di misurazione. Definiamo un fattore “rendimento accademico” per ciascuna delle 3 occasioni, utilizzando le variabili di matematica, scienze e lettura relative a quella misurazione temporale.
Anche se il fattore comune può essere interpretato in modo simile in ciascuna occasione di misurazione (ad esempio, chiamato “rendimento accademico”), questo modello non impone o assume che i fattori specifici per il tempo misurino lo stesso costrutto o che siano misurati sulla stessa scala.
Definiamo il modello nella sintassi di lavaan.
configural_invar <- " #opening quote
#factor loadings
eta1 =~ lambda_S*s_g3+ #for identification
lambda_R3*r_g3+
lambda_M3*m_g3
eta2 =~ lambda_S*s_g5+ #for identification
lambda_R5*r_g5+
lambda_M5*m_g5
eta3 =~ lambda_S*s_g8+ #for identification
lambda_R8*r_g8+
lambda_M8*m_g8
#latent variable variances
eta1~~1*eta1 #for scaling
eta2~~eta2
eta3~~eta3
#latent variable covariances
eta1~~eta2
eta1~~eta3
eta2~~eta3
#unique variances
s_g3~~s_g3
s_g5~~s_g5
s_g8~~s_g8
r_g3~~r_g3
r_g5~~r_g5
r_g8~~r_g8
m_g3~~m_g3
m_g5~~m_g5
m_g8~~m_g8
#unique covariances
s_g3~~s_g5
s_g3~~s_g8
s_g5~~s_g8
r_g3~~r_g5
r_g3~~r_g8
r_g5~~r_g8
m_g3~~m_g5
m_g3~~m_g8
m_g5~~m_g8
#latent variable intercepts
eta1~0*1 #for scaling
eta2~1
eta3~1
#observed variable intercepts
s_g3~tau_S*1
s_g5~tau_S*1
s_g8~tau_S*1
r_g3~tau_R3*1
r_g5~tau_R5*1
r_g8~tau_R8*1
m_g3~tau_M3*1
m_g5~tau_M5*1
m_g8~tau_M8*1
" # closing quote
Adattiamo il modello ai dati.
fit_configural <- lavaan(configural_invar, data = dat, mimic = "mplus")
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING: some cases are empty and will be ignored:
1 2 5 6 9 11 17 26 37 43 44 53 59 61 65 66 73 77 78 81 90 91 94 95 105 106 108 109 112 115 119 120 125 126 127 129 132 136 137 142 149 150 153 155 156 158 159 160 161 162 164 170 172 176 177 178 180 181 182 183 186 191 192 193 199 206 211 213 218 231 232 237 239 241 260 263 264 271 273 276 279 281 299 300 301 308 310 315 323 324 325 326 327 350 351 352 353 356 362 364 370 372 373 375 376 378 381 386 387 392 393 402 403 404 405 406 409 412 415 420 421 422 429 438 439 443 444 449 455 458 462 464 470 476 478 480 481 483 484 485 486 489 491 494 503 508 518 523 524 541 543 548 552 554 559 561 565 569 573 574 576 579 587 593 595 600 605 607 627 632 642 643 644 646 647 648 663 664 665 666 667 677 680 682 683 687 693 695 698 701 704 713 717 719 720 731 733 734 736 751 755 758 763 764 765 767 768 769 770 772 774 781 782 799 802 818 820 822 827 829 843 846 848 850 857 860 875 878 879 883 891 892 895 897 898 899 900 906 910 911 912 913 915 916 917 918 919 920 923 926 928 929 932 936 938 945 946 948 959 960 964 966 969 970 976 978 980 981 982 983 990 992 993 994 997 998 1002 1005 1009 1016 1022 1025 1035 1043 1044 1045 1047 1054 1056 1057 1061 1062 1080 1087 1088 1090 1095 1096 1098 1099 1104 1105 1106 1107 1109 1113 1115 1117 1118 1125 1126 1127 1128 1129 1131 1133 1139 1146 1149 1152 1153 1157 1163 1164 1165 1167 1172 1183 1185 1186 1195 1198 1200 1202 1211 1215 1218 1228 1229 1236 1238 1247 1248 1249 1250 1251 1252 1255 1259 1262 1263 1264 1266 1267 1270 1275 1276 1277 1279 1280 1281 1286 1289 1290 1302 1303 1306 1309 1310 1311 1314 1317 1320 1329 1330 1336 1338 1339 1343 1344 1353 1354 1356 1357 1358 1360 1367 1372 1379 1384 1386 1389 1399 1403 1405 1410 1411 1412 1414 1418 1421 1422 1423 1428 1429 1430 1434 1437 1439 1441 1445 1449 1451 1455 1459 1462 1464 1465 1466 1467 1469 1471 1480 1483 1487 1488 1493 1496 1497 1506 1507 1516 1528 1530 1531 1533 1534 1535 1536 1537 1538 1543 1544 1545 1549 1553 1555 1556 1557 1558 1559 1562 1565 1568 1570 1573 1579 1580 1581 1586 1587 1593 1594 1597 1601 1602 1605 1606 1610 1612 1615 1620 1622 1626 1629 1634 1636 1638 1648 1654 1657 1659 1662 1663 1669 1670 1671 1672 1681 1682 1685 1686 1687 1688 1690 1699 1702 1705 1706 1710 1712 1717 1719 1720 1727 1728 1729 1736 1742 1745 1748 1751 1762 1765 1766 1771 1777 1778 1780 1787 1788 1789 1790 1794 1796 1797 1804 1809 1822 1826 1828 1831 1836 1838 1839 1840 1841 1844 1845 1846 1854 1855 1860 1862 1863 1865 1866 1867 1869 1874 1875 1876 1878 1879 1885 1886 1891 1895 1897 1899 1902 1903 1906 1911 1914 1915 1916 1924 1925 1926 1930 1931 1933 1943 1944 1950 1954 1959 1960 1964 1965 1969 1978 1980 1985 1986 1990 1993 1994 1996 1997 2000 2004 2008 2009 2010 2012 2013 2014 2016 2017 2019 2021 2029 2030 2031 2032 2033 2034 2035 2043 2045 2050 2051 2052 2053 2056 2061 2066 2069 2073 2075 2076 2079 2080 2090 2101 2102 2105 2108”
Esaminiamo la soluzione.
summary(fit_configural, fit.measures = TRUE) |>
print()
lavaan 0.6.15 ended normally after 282 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 43
Number of equality constraints 4
Used Total
Number of observations 1478 2108
Number of missing patterns 24
Model Test User Model:
Test statistic 35.522
Degrees of freedom 15
P-value (Chi-square) 0.002
Model Test Baseline Model:
Test statistic 11669.413
Degrees of freedom 36
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.998
Tucker-Lewis Index (TLI) 0.996
Robust Comparative Fit Index (CFI) 0.998
Robust Tucker-Lewis Index (TLI) 0.995
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -41918.095
Loglikelihood unrestricted model (H1) -41900.334
Akaike (AIC) 83914.190
Bayesian (BIC) 84120.830
Sample-size adjusted Bayesian (SABIC) 83996.938
Root Mean Square Error of Approximation:
RMSEA 0.030
90 Percent confidence interval - lower 0.018
90 Percent confidence interval - upper 0.043
P-value H_0: RMSEA <= 0.050 0.994
P-value H_0: RMSEA >= 0.080 0.000
Robust RMSEA 0.037
90 Percent confidence interval - lower 0.021
90 Percent confidence interval - upper 0.053
P-value H_0: Robust RMSEA <= 0.050 0.897
P-value H_0: Robust RMSEA >= 0.080 0.000
Standardized Root Mean Square Residual:
SRMR 0.008
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta1 =~
s_g3 (lm_S) 13.269 0.339 39.163 0.000
r_g3 (l_R3) 26.301 0.627 41.921 0.000
m_g3 (l_M3) 21.601 0.553 39.074 0.000
eta2 =~
s_g5 (lm_S) 13.269 0.339 39.163 0.000
r_g5 (l_R5) 22.745 0.698 32.598 0.000
m_g5 (l_M5) 20.066 0.631 31.789 0.000
eta3 =~
s_g8 (lm_S) 13.269 0.339 39.163 0.000
r_g8 (l_R8) 21.663 0.753 28.763 0.000
m_g8 (l_M8) 17.259 0.593 29.129 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
eta1 ~~
eta2 1.034 0.021 49.169 0.000
eta3 1.050 0.029 36.246 0.000
eta2 ~~
eta3 1.176 0.048 24.703 0.000
.s_g3 ~~
.s_g5 34.822 3.060 11.379 0.000
.s_g8 14.743 3.006 4.904 0.000
.s_g5 ~~
.s_g8 18.619 3.177 5.861 0.000
.r_g3 ~~
.r_g5 82.590 9.155 9.021 0.000
.r_g8 54.235 9.416 5.760 0.000
.r_g5 ~~
.r_g8 60.822 9.129 6.663 0.000
.m_g3 ~~
.m_g5 123.727 8.135 15.208 0.000
.m_g8 82.025 6.914 11.864 0.000
.m_g5 ~~
.m_g8 91.527 7.139 12.821 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
eta1 0.000
eta2 1.040 0.033 31.645 0.000
eta3 2.435 0.068 35.961 0.000
.s_g3 (ta_S) 51.013 0.407 125.219 0.000
.s_g5 (ta_S) 51.013 0.407 125.219 0.000
.s_g8 (ta_S) 51.013 0.407 125.219 0.000
.r_g3 (t_R3) 127.260 0.772 164.876 0.000
.r_g5 (t_R5) 126.654 0.997 127.087 0.000
.r_g8 (t_R8) 116.432 1.678 69.373 0.000
.m_g3 (t_M3) 99.744 0.668 149.395 0.000
.m_g5 (t_M5) 102.902 0.908 113.381 0.000
.m_g8 (t_M8) 98.540 1.315 74.929 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
eta1 1.000
eta2 1.160 0.046 25.220 0.000
eta3 1.329 0.069 19.227 0.000
.s_g3 67.122 3.535 18.989 0.000
.s_g5 63.195 3.842 16.447 0.000
.s_g8 53.716 4.113 13.059 0.000
.r_g3 180.361 11.527 15.647 0.000
.r_g5 162.710 10.586 15.371 0.000
.r_g8 185.198 12.274 15.089 0.000
.m_g3 187.384 9.448 19.833 0.000
.m_g5 176.465 9.534 18.510 0.000
.m_g8 126.219 7.760 16.265 0.000
Generiamo il diagramma di percorso.
semPlot::semPaths(
fit_configural, "std",
layout = "tree", sizeMan = 7, sizeLat = 7, sizeInt = 4,
residuals = TRUE, rotation = 1, intAtSide = FALSE,
whatLabels = "est", nCharNodes = 0, curvature = 3,
posCol = c("black"), edge.label.cex = .75
)
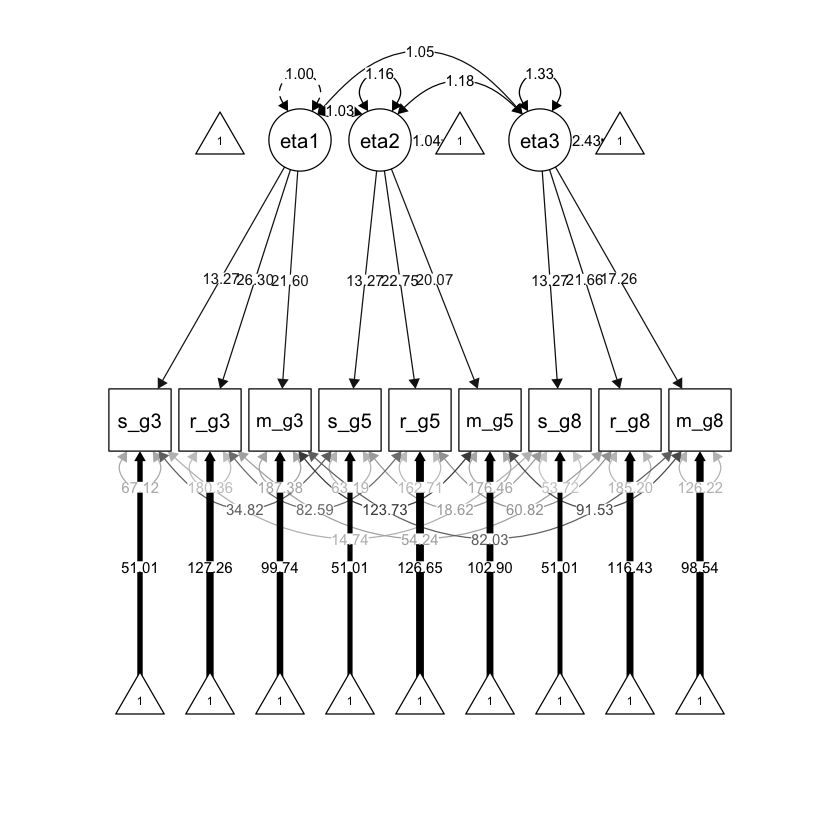
36.2.2. Modello di invarianza debole#
Il modello di invarianza debole impone che la matrice di saturazioni fattoriali sia identica in tutte le occasioni di misurazione. Questo implica che le strutture di covarianza nel tempo siano proporzionali. Tuttavia, il modello permette che le intercette delle variabili osservate possano variare nel tempo e quindi non consente di esaminare il cambiamento longitudinale del fattore.
Definiamo il modello usando la sintassi di lavaan.
weak_invar <- " #opening quote
#factor loadings
eta1 =~ lambda_S*s_g3+ #removed time-specific subscripts
lambda_R*r_g3+
lambda_M*m_g3
eta2 =~ lambda_S*s_g5+
lambda_R*r_g5+
lambda_M*m_g5
eta3 =~ lambda_S*s_g8+
lambda_R*r_g8+
lambda_M*m_g8
#latent variable variances
eta1~~1*eta1
eta2~~eta2
eta3~~eta3
#latent variable covariances
eta1~~eta2
eta1~~eta3
eta2~~eta3
#unique variances
s_g3~~s_g3
s_g5~~s_g5
s_g8~~s_g8
r_g3~~r_g3
r_g5~~r_g5
r_g8~~r_g8
m_g3~~m_g3
m_g5~~m_g5
m_g8~~m_g8
#unique covariances
s_g3~~s_g5
s_g3~~s_g8
s_g5~~s_g8
r_g3~~r_g5
r_g3~~r_g8
r_g5~~r_g8
m_g3~~m_g5
m_g3~~m_g8
m_g5~~m_g8
#latent variable intercepts
eta1~0*1
eta2~1
eta3~1
#observed variable intercepts
s_g3~tau_S*1
s_g5~tau_S*1
s_g8~tau_S*1
r_g3~tau_R3*1
r_g5~tau_R5*1
r_g8~tau_R8*1
m_g3~tau_M3*1
m_g5~tau_M5*1
m_g8~tau_M8*1
" # closing quote
Adattiamo il modello ai dati.
fit_weak <- lavaan(weak_invar, data = dat, mimic = "mplus")
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING: some cases are empty and will be ignored:
1 2 5 6 9 11 17 26 37 43 44 53 59 61 65 66 73 77 78 81 90 91 94 95 105 106 108 109 112 115 119 120 125 126 127 129 132 136 137 142 149 150 153 155 156 158 159 160 161 162 164 170 172 176 177 178 180 181 182 183 186 191 192 193 199 206 211 213 218 231 232 237 239 241 260 263 264 271 273 276 279 281 299 300 301 308 310 315 323 324 325 326 327 350 351 352 353 356 362 364 370 372 373 375 376 378 381 386 387 392 393 402 403 404 405 406 409 412 415 420 421 422 429 438 439 443 444 449 455 458 462 464 470 476 478 480 481 483 484 485 486 489 491 494 503 508 518 523 524 541 543 548 552 554 559 561 565 569 573 574 576 579 587 593 595 600 605 607 627 632 642 643 644 646 647 648 663 664 665 666 667 677 680 682 683 687 693 695 698 701 704 713 717 719 720 731 733 734 736 751 755 758 763 764 765 767 768 769 770 772 774 781 782 799 802 818 820 822 827 829 843 846 848 850 857 860 875 878 879 883 891 892 895 897 898 899 900 906 910 911 912 913 915 916 917 918 919 920 923 926 928 929 932 936 938 945 946 948 959 960 964 966 969 970 976 978 980 981 982 983 990 992 993 994 997 998 1002 1005 1009 1016 1022 1025 1035 1043 1044 1045 1047 1054 1056 1057 1061 1062 1080 1087 1088 1090 1095 1096 1098 1099 1104 1105 1106 1107 1109 1113 1115 1117 1118 1125 1126 1127 1128 1129 1131 1133 1139 1146 1149 1152 1153 1157 1163 1164 1165 1167 1172 1183 1185 1186 1195 1198 1200 1202 1211 1215 1218 1228 1229 1236 1238 1247 1248 1249 1250 1251 1252 1255 1259 1262 1263 1264 1266 1267 1270 1275 1276 1277 1279 1280 1281 1286 1289 1290 1302 1303 1306 1309 1310 1311 1314 1317 1320 1329 1330 1336 1338 1339 1343 1344 1353 1354 1356 1357 1358 1360 1367 1372 1379 1384 1386 1389 1399 1403 1405 1410 1411 1412 1414 1418 1421 1422 1423 1428 1429 1430 1434 1437 1439 1441 1445 1449 1451 1455 1459 1462 1464 1465 1466 1467 1469 1471 1480 1483 1487 1488 1493 1496 1497 1506 1507 1516 1528 1530 1531 1533 1534 1535 1536 1537 1538 1543 1544 1545 1549 1553 1555 1556 1557 1558 1559 1562 1565 1568 1570 1573 1579 1580 1581 1586 1587 1593 1594 1597 1601 1602 1605 1606 1610 1612 1615 1620 1622 1626 1629 1634 1636 1638 1648 1654 1657 1659 1662 1663 1669 1670 1671 1672 1681 1682 1685 1686 1687 1688 1690 1699 1702 1705 1706 1710 1712 1717 1719 1720 1727 1728 1729 1736 1742 1745 1748 1751 1762 1765 1766 1771 1777 1778 1780 1787 1788 1789 1790 1794 1796 1797 1804 1809 1822 1826 1828 1831 1836 1838 1839 1840 1841 1844 1845 1846 1854 1855 1860 1862 1863 1865 1866 1867 1869 1874 1875 1876 1878 1879 1885 1886 1891 1895 1897 1899 1902 1903 1906 1911 1914 1915 1916 1924 1925 1926 1930 1931 1933 1943 1944 1950 1954 1959 1960 1964 1965 1969 1978 1980 1985 1986 1990 1993 1994 1996 1997 2000 2004 2008 2009 2010 2012 2013 2014 2016 2017 2019 2021 2029 2030 2031 2032 2033 2034 2035 2043 2045 2050 2051 2052 2053 2056 2061 2066 2069 2073 2075 2076 2079 2080 2090 2101 2102 2105 2108”
Esaminiamo la soluzione.
out = summary(fit_weak, fit.measures = TRUE)
print(out)
lavaan 0.6.15 ended normally after 208 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 43
Number of equality constraints 8
Used Total
Number of observations 1478 2108
Number of missing patterns 24
Model Test User Model:
Test statistic 116.826
Degrees of freedom 19
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 11669.413
Degrees of freedom 36
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.992
Tucker-Lewis Index (TLI) 0.984
Robust Comparative Fit Index (CFI) 0.991
Robust Tucker-Lewis Index (TLI) 0.983
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -41958.747
Loglikelihood unrestricted model (H1) -41900.334
Akaike (AIC) 83987.495
Bayesian (BIC) 84172.940
Sample-size adjusted Bayesian (SABIC) 84061.756
Root Mean Square Error of Approximation:
RMSEA 0.059
90 Percent confidence interval - lower 0.049
90 Percent confidence interval - upper 0.070
P-value H_0: RMSEA <= 0.050 0.069
P-value H_0: RMSEA >= 0.080 0.000
Robust RMSEA 0.071
90 Percent confidence interval - lower 0.059
90 Percent confidence interval - upper 0.084
P-value H_0: Robust RMSEA <= 0.050 0.003
P-value H_0: Robust RMSEA >= 0.080 0.134
Standardized Root Mean Square Residual:
SRMR 0.062
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta1 =~
s_g3 (lm_S) 14.148 0.328 43.128 0.000
r_g3 (lm_R) 25.418 0.590 43.112 0.000
m_g3 (lm_M) 20.876 0.524 39.821 0.000
eta2 =~
s_g5 (lm_S) 14.148 0.328 43.128 0.000
r_g5 (lm_R) 25.418 0.590 43.112 0.000
m_g5 (lm_M) 20.876 0.524 39.821 0.000
eta3 =~
s_g8 (lm_S) 14.148 0.328 43.128 0.000
r_g8 (lm_R) 25.418 0.590 43.112 0.000
m_g8 (lm_M) 20.876 0.524 39.821 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
eta1 ~~
eta2 0.961 0.014 71.113 0.000
eta3 0.902 0.019 47.928 0.000
eta2 ~~
eta3 0.936 0.027 34.664 0.000
.s_g3 ~~
.s_g5 33.360 3.070 10.866 0.000
.s_g8 14.355 3.054 4.700 0.000
.s_g5 ~~
.s_g8 22.119 3.248 6.811 0.000
.r_g3 ~~
.r_g5 78.937 9.183 8.596 0.000
.r_g8 52.347 9.433 5.549 0.000
.r_g5 ~~
.r_g8 54.402 9.102 5.977 0.000
.m_g3 ~~
.m_g5 129.396 8.261 15.664 0.000
.m_g8 82.602 7.027 11.754 0.000
.m_g5 ~~
.m_g8 92.414 7.292 12.673 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
eta1 0.000
eta2 0.977 0.029 33.565 0.000
eta3 2.293 0.059 38.788 0.000
.s_g3 (ta_S) 51.012 0.424 120.209 0.000
.s_g5 (ta_S) 51.012 0.424 120.209 0.000
.s_g8 (ta_S) 51.012 0.424 120.209 0.000
.r_g3 (t_R3) 127.284 0.755 168.686 0.000
.r_g5 (t_R5) 125.448 0.985 127.310 0.000
.r_g8 (t_R8) 110.884 1.494 74.231 0.000
.m_g3 (t_M3) 99.743 0.656 152.160 0.000
.m_g5 (t_M5) 103.390 0.860 120.251 0.000
.m_g8 (t_M8) 92.568 1.288 71.896 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
eta1 1.000
eta2 1.000 0.026 37.899 0.000
eta3 0.979 0.036 27.053 0.000
.s_g3 63.797 3.533 18.060 0.000
.s_g5 64.271 3.837 16.751 0.000
.s_g8 62.052 4.178 14.851 0.000
.r_g3 187.090 11.494 16.277 0.000
.r_g5 153.835 10.547 14.585 0.000
.r_g8 179.482 12.171 14.746 0.000
.m_g3 194.484 9.513 20.443 0.000
.m_g5 183.051 9.672 18.926 0.000
.m_g8 122.637 7.860 15.603 0.000
Generiamo diagramma di percorso.
semPlot::semPaths(
fit_weak, "std",
layout = "tree", sizeMan = 7, sizeLat = 7, sizeInt = 4,
residuals = TRUE, rotation = 1, intAtSide = FALSE,
whatLabels = "est", nCharNodes = 0, curvature = 3,
posCol = c("black"), edge.label.cex = .75
)
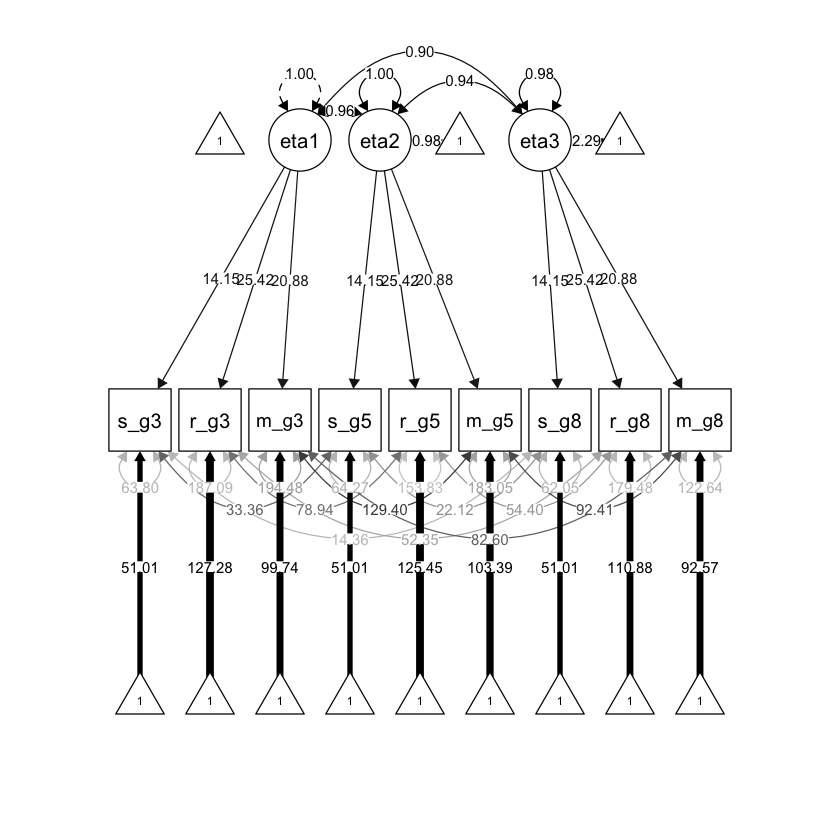
36.2.3. Modello di invarianza forte#
Il modello di invarianza forte impone che le intercette delle variabili osservate siano uguali nel tempo, mentre le medie delle variabili latenti possono variare nelle diverse occasioni. Poiché tutti i cambiamenti nelle medie delle variabili osservate sono attribuiti ai fattori, la scala delle variabili latenti è uguale nelle diverse occasioni di misurazione.
Scriviamo il modello nella sintassi di lavaan.
strong_invar <- " #opening quote
#factor loadings
eta1 =~ lambda_S*s_g3+ #removed time-specific subscripts
lambda_R*r_g3+
lambda_M*m_g3
eta2 =~ lambda_S*s_g5+
lambda_R*r_g5+
lambda_M*m_g5
eta3 =~ lambda_S*s_g8+
lambda_R*r_g8+
lambda_M*m_g8
#latent variable variances
eta1~~1*eta1
eta2~~eta2
eta3~~eta3
#latent variable covariances
eta1~~eta2
eta1~~eta3
eta2~~eta3
#unique variances
s_g3~~s_g3
s_g5~~s_g5
s_g8~~s_g8
r_g3~~r_g3
r_g5~~r_g5
r_g8~~r_g8
m_g3~~m_g3
m_g5~~m_g5
m_g8~~m_g8
#unique covariances
s_g3~~s_g5
s_g3~~s_g8
s_g5~~s_g8
r_g3~~r_g5
r_g3~~r_g8
r_g5~~r_g8
m_g3~~m_g5
m_g3~~m_g8
m_g5~~m_g8
#latent variable intercepts
eta1~0*1
eta2~1
eta3~1
#observed variable intercepts
s_g3~tau_S*1 #removed time-specific subscripts
s_g5~tau_S*1
s_g8~tau_S*1
r_g3~tau_R*1
r_g5~tau_R*1
r_g8~tau_R*1
m_g3~tau_M*1
m_g5~tau_M*1
m_g8~tau_M*1
" # closing quote
Adattiamo il modello ai dati.
fit_strong <- lavaan(strong_invar, data = dat, mimic = "mplus")
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING: some cases are empty and will be ignored:
1 2 5 6 9 11 17 26 37 43 44 53 59 61 65 66 73 77 78 81 90 91 94 95 105 106 108 109 112 115 119 120 125 126 127 129 132 136 137 142 149 150 153 155 156 158 159 160 161 162 164 170 172 176 177 178 180 181 182 183 186 191 192 193 199 206 211 213 218 231 232 237 239 241 260 263 264 271 273 276 279 281 299 300 301 308 310 315 323 324 325 326 327 350 351 352 353 356 362 364 370 372 373 375 376 378 381 386 387 392 393 402 403 404 405 406 409 412 415 420 421 422 429 438 439 443 444 449 455 458 462 464 470 476 478 480 481 483 484 485 486 489 491 494 503 508 518 523 524 541 543 548 552 554 559 561 565 569 573 574 576 579 587 593 595 600 605 607 627 632 642 643 644 646 647 648 663 664 665 666 667 677 680 682 683 687 693 695 698 701 704 713 717 719 720 731 733 734 736 751 755 758 763 764 765 767 768 769 770 772 774 781 782 799 802 818 820 822 827 829 843 846 848 850 857 860 875 878 879 883 891 892 895 897 898 899 900 906 910 911 912 913 915 916 917 918 919 920 923 926 928 929 932 936 938 945 946 948 959 960 964 966 969 970 976 978 980 981 982 983 990 992 993 994 997 998 1002 1005 1009 1016 1022 1025 1035 1043 1044 1045 1047 1054 1056 1057 1061 1062 1080 1087 1088 1090 1095 1096 1098 1099 1104 1105 1106 1107 1109 1113 1115 1117 1118 1125 1126 1127 1128 1129 1131 1133 1139 1146 1149 1152 1153 1157 1163 1164 1165 1167 1172 1183 1185 1186 1195 1198 1200 1202 1211 1215 1218 1228 1229 1236 1238 1247 1248 1249 1250 1251 1252 1255 1259 1262 1263 1264 1266 1267 1270 1275 1276 1277 1279 1280 1281 1286 1289 1290 1302 1303 1306 1309 1310 1311 1314 1317 1320 1329 1330 1336 1338 1339 1343 1344 1353 1354 1356 1357 1358 1360 1367 1372 1379 1384 1386 1389 1399 1403 1405 1410 1411 1412 1414 1418 1421 1422 1423 1428 1429 1430 1434 1437 1439 1441 1445 1449 1451 1455 1459 1462 1464 1465 1466 1467 1469 1471 1480 1483 1487 1488 1493 1496 1497 1506 1507 1516 1528 1530 1531 1533 1534 1535 1536 1537 1538 1543 1544 1545 1549 1553 1555 1556 1557 1558 1559 1562 1565 1568 1570 1573 1579 1580 1581 1586 1587 1593 1594 1597 1601 1602 1605 1606 1610 1612 1615 1620 1622 1626 1629 1634 1636 1638 1648 1654 1657 1659 1662 1663 1669 1670 1671 1672 1681 1682 1685 1686 1687 1688 1690 1699 1702 1705 1706 1710 1712 1717 1719 1720 1727 1728 1729 1736 1742 1745 1748 1751 1762 1765 1766 1771 1777 1778 1780 1787 1788 1789 1790 1794 1796 1797 1804 1809 1822 1826 1828 1831 1836 1838 1839 1840 1841 1844 1845 1846 1854 1855 1860 1862 1863 1865 1866 1867 1869 1874 1875 1876 1878 1879 1885 1886 1891 1895 1897 1899 1902 1903 1906 1911 1914 1915 1916 1924 1925 1926 1930 1931 1933 1943 1944 1950 1954 1959 1960 1964 1965 1969 1978 1980 1985 1986 1990 1993 1994 1996 1997 2000 2004 2008 2009 2010 2012 2013 2014 2016 2017 2019 2021 2029 2030 2031 2032 2033 2034 2035 2043 2045 2050 2051 2052 2053 2056 2061 2066 2069 2073 2075 2076 2079 2080 2090 2101 2102 2105 2108”
Esaminiamo la soluzione.
out = summary(fit_strong, fit.measures = TRUE)
print(out)
lavaan 0.6.15 ended normally after 218 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 43
Number of equality constraints 12
Used Total
Number of observations 1478 2108
Number of missing patterns 24
Model Test User Model:
Test statistic 540.750
Degrees of freedom 23
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 11669.413
Degrees of freedom 36
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.955
Tucker-Lewis Index (TLI) 0.930
Robust Comparative Fit Index (CFI) 0.957
Robust Tucker-Lewis Index (TLI) 0.932
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -42170.709
Loglikelihood unrestricted model (H1) -41900.334
Akaike (AIC) 84403.419
Bayesian (BIC) 84567.670
Sample-size adjusted Bayesian (SABIC) 84469.193
Root Mean Square Error of Approximation:
RMSEA 0.123
90 Percent confidence interval - lower 0.115
90 Percent confidence interval - upper 0.133
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 1.000
Robust RMSEA 0.142
90 Percent confidence interval - lower 0.132
90 Percent confidence interval - upper 0.154
P-value H_0: Robust RMSEA <= 0.050 0.000
P-value H_0: Robust RMSEA >= 0.080 1.000
Standardized Root Mean Square Residual:
SRMR 0.096
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta1 =~
s_g3 (lm_S) 15.088 0.322 46.858 0.000
r_g3 (lm_R) 22.740 0.524 43.414 0.000
m_g3 (lm_M) 20.807 0.473 44.030 0.000
eta2 =~
s_g5 (lm_S) 15.088 0.322 46.858 0.000
r_g5 (lm_R) 22.740 0.524 43.414 0.000
m_g5 (lm_M) 20.807 0.473 44.030 0.000
eta3 =~
s_g8 (lm_S) 15.088 0.322 46.858 0.000
r_g8 (lm_R) 22.740 0.524 43.414 0.000
m_g8 (lm_M) 20.807 0.473 44.030 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
eta1 ~~
eta2 0.976 0.014 70.707 0.000
eta3 0.910 0.019 47.377 0.000
eta2 ~~
eta3 0.961 0.028 34.465 0.000
.s_g3 ~~
.s_g5 29.487 3.487 8.456 0.000
.s_g8 7.394 3.251 2.274 0.023
.s_g5 ~~
.s_g8 7.867 3.332 2.361 0.018
.r_g3 ~~
.r_g5 109.044 9.413 11.585 0.000
.r_g8 73.172 9.982 7.330 0.000
.r_g5 ~~
.r_g8 71.480 9.209 7.762 0.000
.m_g3 ~~
.m_g5 128.408 8.511 15.088 0.000
.m_g8 85.516 7.421 11.523 0.000
.m_g5 ~~
.m_g8 90.389 7.594 11.903 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
eta1 0.000
eta2 1.032 0.026 40.382 0.000
eta3 1.972 0.046 42.668 0.000
.s_g3 (ta_S) 51.422 0.450 114.287 0.000
.s_g5 (ta_S) 51.422 0.450 114.287 0.000
.s_g8 (ta_S) 51.422 0.450 114.287 0.000
.r_g3 (ta_R) 126.310 0.706 179.023 0.000
.r_g5 (ta_R) 126.310 0.706 179.023 0.000
.r_g8 (ta_R) 126.310 0.706 179.023 0.000
.m_g3 (ta_M) 100.035 0.658 152.097 0.000
.m_g5 (ta_M) 100.035 0.658 152.097 0.000
.m_g8 (ta_M) 100.035 0.658 152.097 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
eta1 1.000
eta2 1.025 0.027 37.549 0.000
eta3 0.990 0.037 26.783 0.000
.s_g3 58.999 3.875 15.224 0.000
.s_g5 63.402 4.314 14.698 0.000
.s_g8 58.256 4.688 12.427 0.000
.r_g3 230.033 11.800 19.494 0.000
.r_g5 181.922 10.581 17.193 0.000
.r_g8 208.269 12.238 17.019 0.000
.m_g3 197.179 9.868 19.981 0.000
.m_g5 188.328 10.123 18.603 0.000
.m_g8 126.741 8.199 15.458 0.000
Generiamo il diagramma di percorso.
semPlot::semPaths(
fit_strong, "std",
layout = "tree", sizeMan = 7, sizeLat = 7, sizeInt = 4,
residuals = TRUE, rotation = 1, intAtSide = FALSE,
whatLabels = "est", nCharNodes = 0, curvature = 3,
posCol = c("black"), edge.label.cex = .75
)
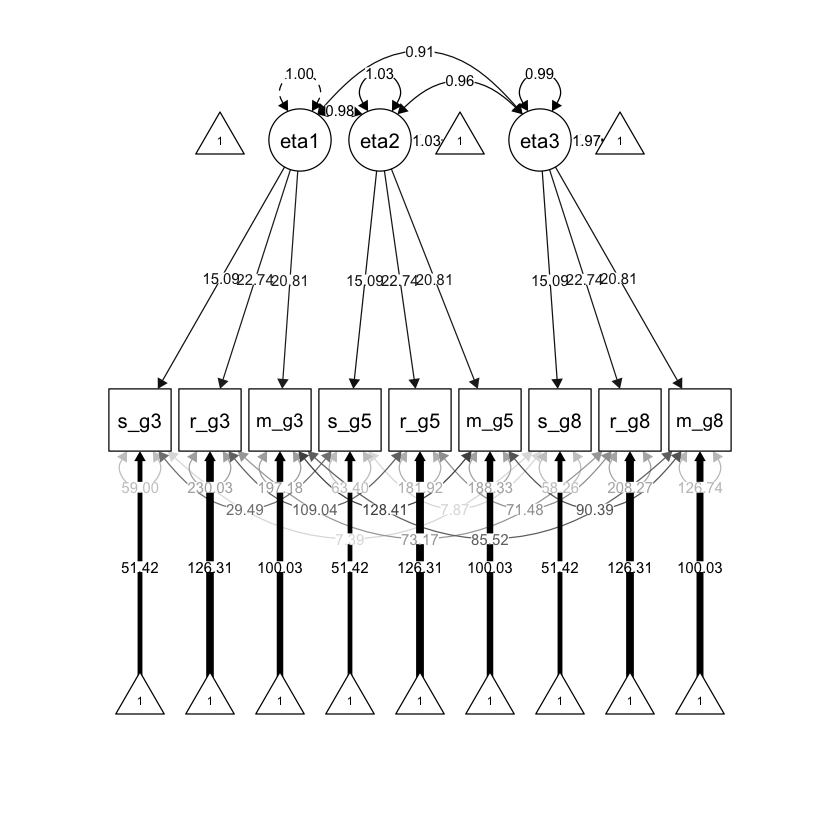
36.2.4. Invarianza stretta#
Il modello di invarianza rigorosa impone vincoli aggiuntivi sulle saturazioni fattoriali, sulle intercette delle variabili osservate e sulle varianze uniche. Quando l’invarianza fattoriale rigorosa è soddisfatta, i cambiamenti longitudinali nelle medie osservate, nelle varianze e nelle covarianze ci informano sui cambiamenti longitudinali dei fattori.
Definiamo il modello con la sintassi di lavaan.
strict_invar <- " #opening quote
#factor loadings
eta1 =~ lambda_S*s_g3+ #removed time-specific subscripts
lambda_R*r_g3+
lambda_M*m_g3
eta2 =~ lambda_S*s_g5+
lambda_R*r_g5+
lambda_M*m_g5
eta3 =~ lambda_S*s_g8+
lambda_R*r_g8+
lambda_M*m_g8
#latent variable variances
eta1~~1*eta1
eta2~~eta2
eta3~~eta3
#latent variable covariances
eta1~~eta2
eta1~~eta3
eta2~~eta3
#unique variances
s_g3~~theta_S*s_g3 #adding constraints with names
s_g5~~theta_S*s_g5
s_g8~~theta_S*s_g8
r_g3~~theta_R*r_g3
r_g5~~theta_R*r_g5
r_g8~~theta_R*r_g8
m_g3~~theta_M*m_g3
m_g5~~theta_M*m_g5
m_g8~~theta_M*m_g8
#unique covariances
s_g3~~s_g5
s_g3~~s_g8
s_g5~~s_g8
r_g3~~r_g5
r_g3~~r_g8
r_g5~~r_g8
m_g3~~m_g5
m_g3~~m_g8
m_g5~~m_g8
#latent variable intercepts
eta1~0*1
eta2~1
eta3~1
#observed variable intercepts
s_g3~tau_S*1 #removed time-specific subscripts
s_g5~tau_S*1
s_g8~tau_S*1
r_g3~tau_R*1
r_g5~tau_R*1
r_g8~tau_R*1
m_g3~tau_M*1
m_g5~tau_M*1
m_g8~tau_M*1
" # closing quote
Adattiamo il modello ai dati.
fit_strict <- lavaan(strict_invar, data = dat, mimic = "mplus")
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING: some cases are empty and will be ignored:
1 2 5 6 9 11 17 26 37 43 44 53 59 61 65 66 73 77 78 81 90 91 94 95 105 106 108 109 112 115 119 120 125 126 127 129 132 136 137 142 149 150 153 155 156 158 159 160 161 162 164 170 172 176 177 178 180 181 182 183 186 191 192 193 199 206 211 213 218 231 232 237 239 241 260 263 264 271 273 276 279 281 299 300 301 308 310 315 323 324 325 326 327 350 351 352 353 356 362 364 370 372 373 375 376 378 381 386 387 392 393 402 403 404 405 406 409 412 415 420 421 422 429 438 439 443 444 449 455 458 462 464 470 476 478 480 481 483 484 485 486 489 491 494 503 508 518 523 524 541 543 548 552 554 559 561 565 569 573 574 576 579 587 593 595 600 605 607 627 632 642 643 644 646 647 648 663 664 665 666 667 677 680 682 683 687 693 695 698 701 704 713 717 719 720 731 733 734 736 751 755 758 763 764 765 767 768 769 770 772 774 781 782 799 802 818 820 822 827 829 843 846 848 850 857 860 875 878 879 883 891 892 895 897 898 899 900 906 910 911 912 913 915 916 917 918 919 920 923 926 928 929 932 936 938 945 946 948 959 960 964 966 969 970 976 978 980 981 982 983 990 992 993 994 997 998 1002 1005 1009 1016 1022 1025 1035 1043 1044 1045 1047 1054 1056 1057 1061 1062 1080 1087 1088 1090 1095 1096 1098 1099 1104 1105 1106 1107 1109 1113 1115 1117 1118 1125 1126 1127 1128 1129 1131 1133 1139 1146 1149 1152 1153 1157 1163 1164 1165 1167 1172 1183 1185 1186 1195 1198 1200 1202 1211 1215 1218 1228 1229 1236 1238 1247 1248 1249 1250 1251 1252 1255 1259 1262 1263 1264 1266 1267 1270 1275 1276 1277 1279 1280 1281 1286 1289 1290 1302 1303 1306 1309 1310 1311 1314 1317 1320 1329 1330 1336 1338 1339 1343 1344 1353 1354 1356 1357 1358 1360 1367 1372 1379 1384 1386 1389 1399 1403 1405 1410 1411 1412 1414 1418 1421 1422 1423 1428 1429 1430 1434 1437 1439 1441 1445 1449 1451 1455 1459 1462 1464 1465 1466 1467 1469 1471 1480 1483 1487 1488 1493 1496 1497 1506 1507 1516 1528 1530 1531 1533 1534 1535 1536 1537 1538 1543 1544 1545 1549 1553 1555 1556 1557 1558 1559 1562 1565 1568 1570 1573 1579 1580 1581 1586 1587 1593 1594 1597 1601 1602 1605 1606 1610 1612 1615 1620 1622 1626 1629 1634 1636 1638 1648 1654 1657 1659 1662 1663 1669 1670 1671 1672 1681 1682 1685 1686 1687 1688 1690 1699 1702 1705 1706 1710 1712 1717 1719 1720 1727 1728 1729 1736 1742 1745 1748 1751 1762 1765 1766 1771 1777 1778 1780 1787 1788 1789 1790 1794 1796 1797 1804 1809 1822 1826 1828 1831 1836 1838 1839 1840 1841 1844 1845 1846 1854 1855 1860 1862 1863 1865 1866 1867 1869 1874 1875 1876 1878 1879 1885 1886 1891 1895 1897 1899 1902 1903 1906 1911 1914 1915 1916 1924 1925 1926 1930 1931 1933 1943 1944 1950 1954 1959 1960 1964 1965 1969 1978 1980 1985 1986 1990 1993 1994 1996 1997 2000 2004 2008 2009 2010 2012 2013 2014 2016 2017 2019 2021 2029 2030 2031 2032 2033 2034 2035 2043 2045 2050 2051 2052 2053 2056 2061 2066 2069 2073 2075 2076 2079 2080 2090 2101 2102 2105 2108”
Esaminiamo la soluzione ottenuta.
out = summary(fit_strict, fit.measures = TRUE)
print(out)
lavaan 0.6.15 ended normally after 260 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 43
Number of equality constraints 18
Used Total
Number of observations 1478 2108
Number of missing patterns 24
Model Test User Model:
Test statistic 600.614
Degrees of freedom 29
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 11669.413
Degrees of freedom 36
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.951
Tucker-Lewis Index (TLI) 0.939
Robust Comparative Fit Index (CFI) 0.952
Robust Tucker-Lewis Index (TLI) 0.940
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -42200.641
Loglikelihood unrestricted model (H1) -41900.334
Akaike (AIC) 84451.282
Bayesian (BIC) 84583.743
Sample-size adjusted Bayesian (SABIC) 84504.325
Root Mean Square Error of Approximation:
RMSEA 0.115
90 Percent confidence interval - lower 0.108
90 Percent confidence interval - upper 0.124
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 1.000
Robust RMSEA 0.134
90 Percent confidence interval - lower 0.125
90 Percent confidence interval - upper 0.144
P-value H_0: Robust RMSEA <= 0.050 0.000
P-value H_0: Robust RMSEA >= 0.080 1.000
Standardized Root Mean Square Residual:
SRMR 0.111
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta1 =~
s_g3 (lm_S) 15.176 0.319 47.527 0.000
r_g3 (lm_R) 22.982 0.520 44.172 0.000
m_g3 (lm_M) 21.236 0.473 44.918 0.000
eta2 =~
s_g5 (lm_S) 15.176 0.319 47.527 0.000
r_g5 (lm_R) 22.982 0.520 44.172 0.000
m_g5 (lm_M) 21.236 0.473 44.918 0.000
eta3 =~
s_g8 (lm_S) 15.176 0.319 47.527 0.000
r_g8 (lm_R) 22.982 0.520 44.172 0.000
m_g8 (lm_M) 21.236 0.473 44.918 0.000
Covariances:
Estimate Std.Err z-value P(>|z|)
eta1 ~~
eta2 0.968 0.013 72.280 0.000
eta3 0.904 0.019 48.240 0.000
eta2 ~~
eta3 0.949 0.027 35.094 0.000
.s_g3 ~~
.s_g5 28.853 3.118 9.254 0.000
.s_g8 6.616 3.301 2.004 0.045
.s_g5 ~~
.s_g8 5.354 3.311 1.617 0.106
.r_g3 ~~
.r_g5 112.069 8.673 12.921 0.000
.r_g8 69.529 9.345 7.440 0.000
.r_g5 ~~
.r_g8 79.188 9.640 8.214 0.000
.m_g3 ~~
.m_g5 112.589 7.308 15.407 0.000
.m_g8 93.467 7.990 11.698 0.000
.m_g5 ~~
.m_g8 102.538 8.014 12.794 0.000
Intercepts:
Estimate Std.Err z-value P(>|z|)
eta1 0.000
eta2 1.020 0.025 41.017 0.000
eta3 1.947 0.045 43.249 0.000
.s_g3 (ta_S) 51.433 0.448 114.745 0.000
.s_g5 (ta_S) 51.433 0.448 114.745 0.000
.s_g8 (ta_S) 51.433 0.448 114.745 0.000
.r_g3 (ta_R) 126.363 0.702 179.899 0.000
.r_g5 (ta_R) 126.363 0.702 179.899 0.000
.r_g8 (ta_R) 126.363 0.702 179.899 0.000
.m_g3 (ta_M) 100.193 0.651 153.913 0.000
.m_g5 (ta_M) 100.193 0.651 153.913 0.000
.m_g8 (ta_M) 100.193 0.651 153.913 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
eta1 1.000
eta2 1.011 0.026 38.332 0.000
eta3 0.971 0.036 27.168 0.000
.s_g3 (th_S) 60.274 2.939 20.506 0.000
.s_g5 (th_S) 60.274 2.939 20.506 0.000
.s_g8 (th_S) 60.274 2.939 20.506 0.000
.r_g3 (th_R) 208.701 8.172 25.537 0.000
.r_g5 (th_R) 208.701 8.172 25.537 0.000
.r_g8 (th_R) 208.701 8.172 25.537 0.000
.m_g3 (th_M) 173.321 7.236 23.952 0.000
.m_g5 (th_M) 173.321 7.236 23.952 0.000
.m_g8 (th_M) 173.321 7.236 23.952 0.000
Generiamo il diagramma di percorso.
semPlot::semPaths(
fit_strict, "std",
layout = "tree", sizeMan = 7, sizeLat = 7, sizeInt = 4,
residuals = TRUE, rotation = 1, intAtSide = FALSE,
whatLabels = "est", nCharNodes = 0, curvature = 3,
posCol = c("black"), edge.label.cex = .75
)
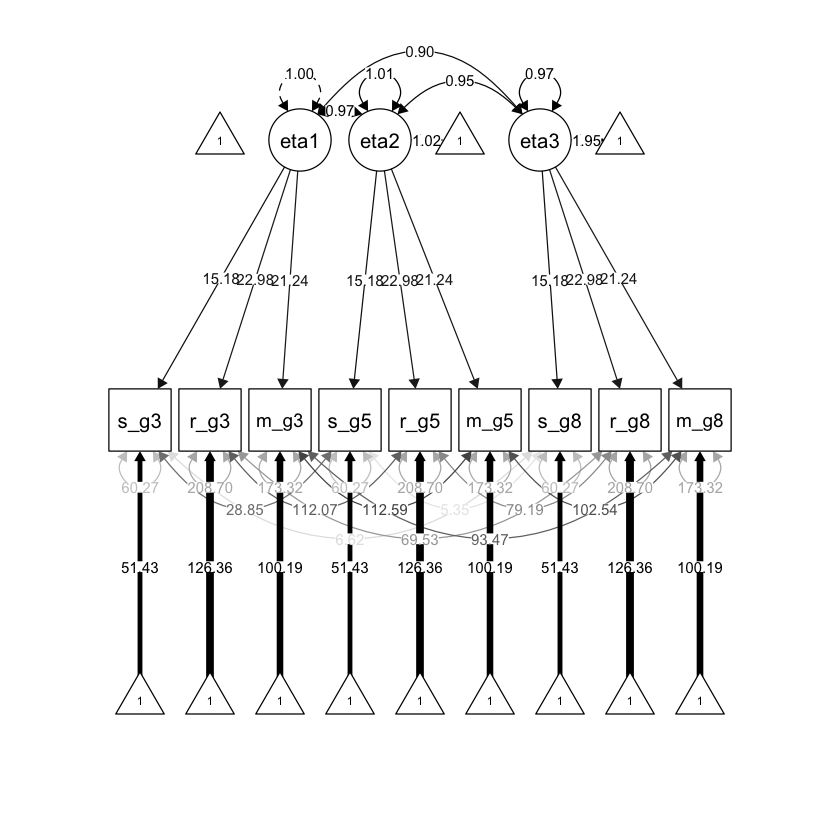
36.3. Confronto tra modelli#
È possibile valutare il tipo di invarianza fattoriale longitudinale giustificata dai dati mediante un confronto tra modelli.
round(cbind(
configural = inspect(fit_configural, "fit.measures"),
weak = inspect(fit_weak, "fit.measures"),
strong = inspect(fit_strong, "fit.measures"),
strict = inspect(fit_strict, "fit.measures")
), 3)
| configural | weak | strong | strict | |
|---|---|---|---|---|
| npar | 39.000 | 35.000 | 31.000 | 25.000 |
| fmin | 0.012 | 0.040 | 0.183 | 0.203 |
| chisq | 35.522 | 116.826 | 540.750 | 600.614 |
| df | 15.000 | 19.000 | 23.000 | 29.000 |
| pvalue | 0.002 | 0.000 | 0.000 | 0.000 |
| baseline.chisq | 11669.413 | 11669.413 | 11669.413 | 11669.413 |
| baseline.df | 36.000 | 36.000 | 36.000 | 36.000 |
| baseline.pvalue | 0.000 | 0.000 | 0.000 | 0.000 |
| cfi | 0.998 | 0.992 | 0.955 | 0.951 |
| tli | 0.996 | 0.984 | 0.930 | 0.939 |
| cfi.robust | 0.998 | 0.991 | 0.957 | 0.952 |
| tli.robust | 0.995 | 0.983 | 0.932 | 0.940 |
| nnfi | 0.996 | 0.984 | 0.930 | 0.939 |
| rfi | 0.993 | 0.981 | 0.927 | 0.936 |
| nfi | 0.997 | 0.990 | 0.954 | 0.949 |
| pnfi | 0.415 | 0.522 | 0.609 | 0.764 |
| ifi | 0.998 | 0.992 | 0.956 | 0.951 |
| rni | 0.998 | 0.992 | 0.955 | 0.951 |
| nnfi.robust | 0.995 | 0.983 | 0.932 | 0.940 |
| rni.robust | 0.998 | 0.991 | 0.957 | 0.952 |
| logl | -41918.095 | -41958.747 | -42170.709 | -42200.641 |
| unrestricted.logl | -41900.334 | -41900.334 | -41900.334 | -41900.334 |
| aic | 83914.190 | 83987.495 | 84403.419 | 84451.282 |
| bic | 84120.830 | 84172.940 | 84567.670 | 84583.743 |
| ntotal | 1478.000 | 1478.000 | 1478.000 | 1478.000 |
| bic2 | 83996.938 | 84061.756 | 84469.193 | 84504.325 |
| rmsea | 0.030 | 0.059 | 0.123 | 0.115 |
| rmsea.ci.lower | 0.018 | 0.049 | 0.115 | 0.108 |
| rmsea.ci.upper | 0.043 | 0.070 | 0.133 | 0.124 |
| rmsea.ci.level | 0.900 | 0.900 | 0.900 | 0.900 |
| rmsea.pvalue | 0.994 | 0.069 | 0.000 | 0.000 |
| rmsea.close.h0 | 0.050 | 0.050 | 0.050 | 0.050 |
| rmsea.notclose.pvalue | 0.000 | 0.000 | 1.000 | 1.000 |
| rmsea.notclose.h0 | 0.080 | 0.080 | 0.080 | 0.080 |
| rmsea.robust | 0.037 | 0.071 | 0.142 | 0.134 |
| rmsea.ci.lower.robust | 0.021 | 0.059 | 0.132 | 0.125 |
| rmsea.ci.upper.robust | 0.053 | 0.084 | 0.154 | 0.144 |
| rmsea.pvalue.robust | 0.897 | 0.003 | 0.000 | 0.000 |
| rmsea.notclose.pvalue.robust | 0.000 | 0.134 | 1.000 | 1.000 |
| rmr | 3.876 | 20.127 | 41.365 | 40.928 |
| rmr_nomean | 4.246 | 22.048 | 45.308 | 44.829 |
| srmr | 0.008 | 0.062 | 0.096 | 0.111 |
| srmr_bentler | 0.007 | 0.042 | 0.075 | 0.078 |
| srmr_bentler_nomean | 0.008 | 0.046 | 0.076 | 0.079 |
| crmr | 0.008 | 0.016 | 0.042 | 0.041 |
| crmr_nomean | 0.009 | 0.018 | 0.028 | 0.027 |
| srmr_mplus | 0.008 | 0.062 | 0.096 | 0.111 |
| srmr_mplus_nomean | 0.008 | 0.030 | 0.050 | 0.055 |
| cn_05 | 1041.031 | 382.354 | 97.135 | 105.725 |
| cn_01 | 1273.294 | 458.860 | 114.808 | 123.027 |
| gfi | 0.997 | 0.996 | 0.991 | 0.990 |
| agfi | 0.990 | 0.989 | 0.980 | 0.982 |
| pgfi | 0.277 | 0.350 | 0.422 | 0.532 |
| mfi | 0.993 | 0.967 | 0.839 | 0.824 |
| ecvi | 0.077 | 0.126 | 0.408 | 0.440 |
# Chi-square difference test for nested models
lavTestLRT(fit_configural, fit_weak) |>
print()
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
fit_configural 15 83914 84121 35.522
fit_weak 19 83987 84173 116.826 81.304 0.11435 4 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
lavTestLRT(fit_weak, fit_strong) |>
print()
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
fit_weak 19 83987 84173 116.83
fit_strong 23 84403 84568 540.75 423.92 0.26651 4 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
lavTestLRT(fit_strong, fit_strict) |>
print()
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
fit_strong 23 84403 84568 540.75
fit_strict 29 84451 84584 600.61 59.863 0.077935 6 4.798e-11 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Nel caso presente, solo l’invarianza configurale è giustificata dal test di verosimiglianze. L’esame degli indici di bontà di adattamento, comunque, suggerisce che l’invarianza debole sembra giustificata per questi dati. @grimm2016growth concludono invece che anche l’invarianza forte è giustificata per questi dati.
36.4. Second-Order Growth Model#
Una volta che abbiamo dimostrato che l’invarianza forte o rigorosa è supportata per il modello di crescita latente, possiamo esaminare i cambiamenti nei punteggi fattoriali.
In questo esempio, imponiamo l’invarianza fattoriale rigorosa e modelliamo il cambiamento nei punteggi fattoriali del rendimento accademico dei bambini utilizzando un Second-Order Growth Model. Si noti che devono essere apportate alcune altre modifiche per l’identificazione e la scala.
growth_strict_invar <- " #opening quote
#factor loadings
eta1 =~ 15.176*s_g3+ #constrained for identification and scaling
lambda_R*r_g3+
lambda_M*m_g3
eta2 =~ 15.176*s_g5+
lambda_R*r_g5+
lambda_M*m_g5
eta3 =~ 15.176*s_g8+
lambda_R*r_g8+
lambda_M*m_g8
#latent variable variances
eta1~~psi*eta1
eta2~~psi*eta2
eta3~~psi*eta3
#latent variable covariances
eta1~~0*eta2 #constrained to zero
eta1~~0*eta3
eta2~~0*eta3
#unique variances
s_g3~~theta_S*s_g3 #adding constraints with names
s_g5~~theta_S*s_g5
s_g8~~theta_S*s_g8
r_g3~~theta_R*r_g3
r_g5~~theta_R*r_g5
r_g8~~theta_R*r_g8
m_g3~~theta_M*m_g3
m_g5~~theta_M*m_g5
m_g8~~theta_M*m_g8
#unique covariances
s_g3~~s_g5
s_g3~~s_g8
s_g5~~s_g8
r_g3~~r_g5
r_g3~~r_g8
r_g5~~r_g8
m_g3~~m_g5
m_g3~~m_g8
m_g5~~m_g8
#latent variable intercepts
eta1~0*1 #fixed to zero
eta2~0*1
eta3~0*1
#observed variable intercepts
s_g3~tau_S*1 #removed time-specific subscripts
s_g5~tau_S*1
s_g8~tau_S*1
r_g3~tau_R*1
r_g5~tau_R*1
r_g8~tau_R*1
m_g3~tau_M*1
m_g5~tau_M*1
m_g8~tau_M*1
#second-order latent basis growth
#growth factors
xi_1 =~ 1*eta1+ #intercept factor
1*eta2+
1*eta3
xi_2 =~ 0*eta1 #latent basis slope factor
+start(0.5)*eta2
+1*eta3
#factor variances & covariance
xi_1~~start(.8)*xi_1
xi_2~~start(.5)*xi_2
xi_1~~start(0)*xi_2
#factor intercepts
xi_1~0*1
xi_2~1
" # closing quote
Adattiamo il modello ai dati.
fit_growth <- lavaan(growth_strict_invar, data = dat, mimic = "mplus")
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING: some cases are empty and will be ignored:
1 2 5 6 9 11 17 26 37 43 44 53 59 61 65 66 73 77 78 81 90 91 94 95 105 106 108 109 112 115 119 120 125 126 127 129 132 136 137 142 149 150 153 155 156 158 159 160 161 162 164 170 172 176 177 178 180 181 182 183 186 191 192 193 199 206 211 213 218 231 232 237 239 241 260 263 264 271 273 276 279 281 299 300 301 308 310 315 323 324 325 326 327 350 351 352 353 356 362 364 370 372 373 375 376 378 381 386 387 392 393 402 403 404 405 406 409 412 415 420 421 422 429 438 439 443 444 449 455 458 462 464 470 476 478 480 481 483 484 485 486 489 491 494 503 508 518 523 524 541 543 548 552 554 559 561 565 569 573 574 576 579 587 593 595 600 605 607 627 632 642 643 644 646 647 648 663 664 665 666 667 677 680 682 683 687 693 695 698 701 704 713 717 719 720 731 733 734 736 751 755 758 763 764 765 767 768 769 770 772 774 781 782 799 802 818 820 822 827 829 843 846 848 850 857 860 875 878 879 883 891 892 895 897 898 899 900 906 910 911 912 913 915 916 917 918 919 920 923 926 928 929 932 936 938 945 946 948 959 960 964 966 969 970 976 978 980 981 982 983 990 992 993 994 997 998 1002 1005 1009 1016 1022 1025 1035 1043 1044 1045 1047 1054 1056 1057 1061 1062 1080 1087 1088 1090 1095 1096 1098 1099 1104 1105 1106 1107 1109 1113 1115 1117 1118 1125 1126 1127 1128 1129 1131 1133 1139 1146 1149 1152 1153 1157 1163 1164 1165 1167 1172 1183 1185 1186 1195 1198 1200 1202 1211 1215 1218 1228 1229 1236 1238 1247 1248 1249 1250 1251 1252 1255 1259 1262 1263 1264 1266 1267 1270 1275 1276 1277 1279 1280 1281 1286 1289 1290 1302 1303 1306 1309 1310 1311 1314 1317 1320 1329 1330 1336 1338 1339 1343 1344 1353 1354 1356 1357 1358 1360 1367 1372 1379 1384 1386 1389 1399 1403 1405 1410 1411 1412 1414 1418 1421 1422 1423 1428 1429 1430 1434 1437 1439 1441 1445 1449 1451 1455 1459 1462 1464 1465 1466 1467 1469 1471 1480 1483 1487 1488 1493 1496 1497 1506 1507 1516 1528 1530 1531 1533 1534 1535 1536 1537 1538 1543 1544 1545 1549 1553 1555 1556 1557 1558 1559 1562 1565 1568 1570 1573 1579 1580 1581 1586 1587 1593 1594 1597 1601 1602 1605 1606 1610 1612 1615 1620 1622 1626 1629 1634 1636 1638 1648 1654 1657 1659 1662 1663 1669 1670 1671 1672 1681 1682 1685 1686 1687 1688 1690 1699 1702 1705 1706 1710 1712 1717 1719 1720 1727 1728 1729 1736 1742 1745 1748 1751 1762 1765 1766 1771 1777 1778 1780 1787 1788 1789 1790 1794 1796 1797 1804 1809 1822 1826 1828 1831 1836 1838 1839 1840 1841 1844 1845 1846 1854 1855 1860 1862 1863 1865 1866 1867 1869 1874 1875 1876 1878 1879 1885 1886 1891 1895 1897 1899 1902 1903 1906 1911 1914 1915 1916 1924 1925 1926 1930 1931 1933 1943 1944 1950 1954 1959 1960 1964 1965 1969 1978 1980 1985 1986 1990 1993 1994 1996 1997 2000 2004 2008 2009 2010 2012 2013 2014 2016 2017 2019 2021 2029 2030 2031 2032 2033 2034 2035 2043 2045 2050 2051 2052 2053 2056 2061 2066 2069 2073 2075 2076 2079 2080 2090 2101 2102 2105 2108”
Esaminiamo la soluzione.
out = summary(fit_growth, fit.measures = TRUE)
print(out)
lavaan 0.6.15 ended normally after 192 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 41
Number of equality constraints 18
Used Total
Number of observations 1478 2108
Number of missing patterns 24
Model Test User Model:
Test statistic 606.985
Degrees of freedom 31
P-value (Chi-square) 0.000
Model Test Baseline Model:
Test statistic 11669.413
Degrees of freedom 36
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.950
Tucker-Lewis Index (TLI) 0.943
Robust Comparative Fit Index (CFI) 0.951
Robust Tucker-Lewis Index (TLI) 0.943
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -42203.827
Loglikelihood unrestricted model (H1) -41900.334
Akaike (AIC) 84453.654
Bayesian (BIC) 84575.518
Sample-size adjusted Bayesian (SABIC) 84502.454
Root Mean Square Error of Approximation:
RMSEA 0.112
90 Percent confidence interval - lower 0.104
90 Percent confidence interval - upper 0.120
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 1.000
Robust RMSEA 0.131
90 Percent confidence interval - lower 0.121
90 Percent confidence interval - upper 0.140
P-value H_0: Robust RMSEA <= 0.050 0.000
P-value H_0: Robust RMSEA >= 0.080 1.000
Standardized Root Mean Square Residual:
SRMR 0.113
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta1 =~
s_g3 15.176
r_g3 (lm_R) 22.991 0.284 81.092 0.000
m_g3 (lm_M) 21.237 0.248 85.618 0.000
eta2 =~
s_g5 15.176
r_g5 (lm_R) 22.991 0.284 81.092 0.000
m_g5 (lm_M) 21.237 0.248 85.618 0.000
eta3 =~
s_g8 15.176
r_g8 (lm_R) 22.991 0.284 81.092 0.000
m_g8 (lm_M) 21.237 0.248 85.618 0.000
xi_1 =~
eta1 1.000
eta2 1.000
eta3 1.000
xi_2 =~
eta1 0.000
eta2 0.524 0.006 85.608 0.000
eta3 1.000
Covariances:
Estimate Std.Err z-value P(>|z|)
.eta1 ~~
.eta2 0.000
.eta3 0.000
.eta2 ~~
.eta3 0.000
.s_g3 ~~
.s_g5 28.704 3.098 9.265 0.000
.s_g8 6.807 3.311 2.056 0.040
.s_g5 ~~
.s_g8 5.742 3.289 1.746 0.081
.r_g3 ~~
.r_g5 113.232 8.622 13.134 0.000
.r_g8 67.856 9.358 7.251 0.000
.r_g5 ~~
.r_g8 78.009 9.529 8.187 0.000
.m_g3 ~~
.m_g5 113.479 7.277 15.594 0.000
.m_g8 92.852 8.000 11.607 0.000
.m_g5 ~~
.m_g8 100.693 7.932 12.694 0.000
xi_1 ~~
xi_2 -0.061 0.019 -3.114 0.002
Intercepts:
Estimate Std.Err z-value P(>|z|)
.eta1 0.000
.eta2 0.000
.eta3 0.000
.s_g3 (ta_S) 51.423 0.449 114.450 0.000
.s_g5 (ta_S) 51.423 0.449 114.450 0.000
.s_g8 (ta_S) 51.423 0.449 114.450 0.000
.r_g3 (ta_R) 126.339 0.704 179.381 0.000
.r_g5 (ta_R) 126.339 0.704 179.381 0.000
.r_g8 (ta_R) 126.339 0.704 179.381 0.000
.m_g3 (ta_M) 100.181 0.653 153.454 0.000
.m_g5 (ta_M) 100.181 0.653 153.454 0.000
.m_g8 (ta_M) 100.181 0.653 153.454 0.000
xi_1 0.000
xi_2 1.947 0.024 82.219 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
.eta1 (psi) 0.024 0.004 6.026 0.000
.eta2 (psi) 0.024 0.004 6.026 0.000
.eta3 (psi) 0.024 0.004 6.026 0.000
.s_g3 (th_S) 60.273 2.929 20.580 0.000
.s_g5 (th_S) 60.273 2.929 20.580 0.000
.s_g8 (th_S) 60.273 2.929 20.580 0.000
.r_g3 (th_R) 208.603 8.162 25.557 0.000
.r_g5 (th_R) 208.603 8.162 25.557 0.000
.r_g8 (th_R) 208.603 8.162 25.557 0.000
.m_g3 (th_M) 173.813 7.217 24.083 0.000
.m_g5 (th_M) 173.813 7.217 24.083 0.000
.m_g8 (th_M) 173.813 7.217 24.083 0.000
xi_1 0.982 0.042 23.184 0.000
xi_2 0.110 0.018 6.277 0.000
Generiamo il diagramma di percorso.
semPlot::semPaths(
fit_growth, "std",
layout = "tree", sizeMan = 7, sizeLat = 7, sizeInt = 4,
residuals = TRUE, rotation = 1, intAtSide = FALSE,
whatLabels = "est", nCharNodes = 0, curvature = 3,
posCol = c("black"), edge.label.cex = .75
)
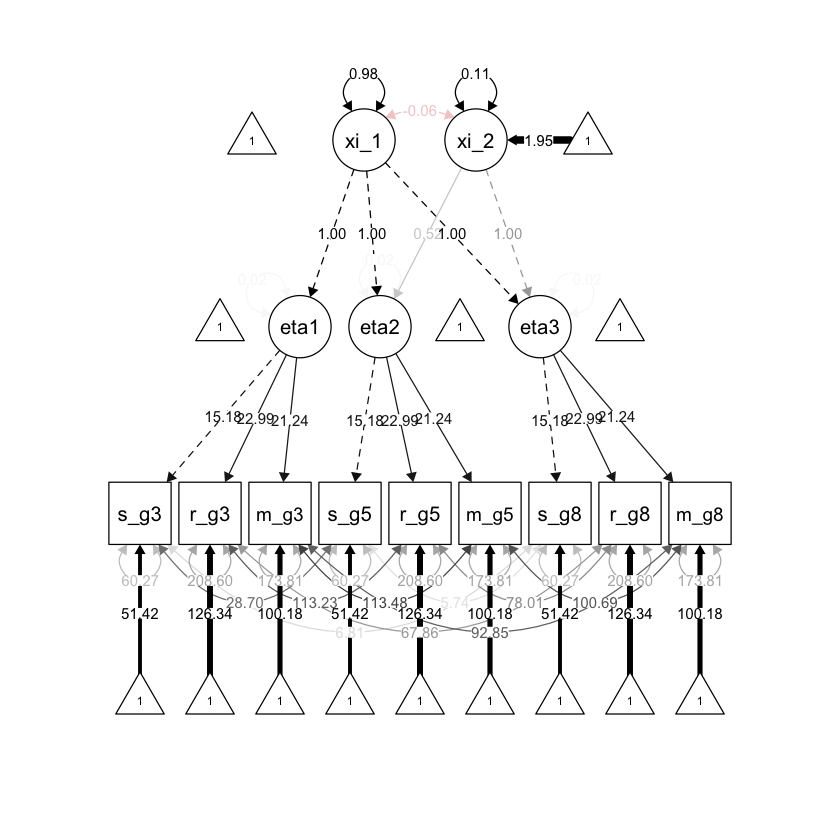
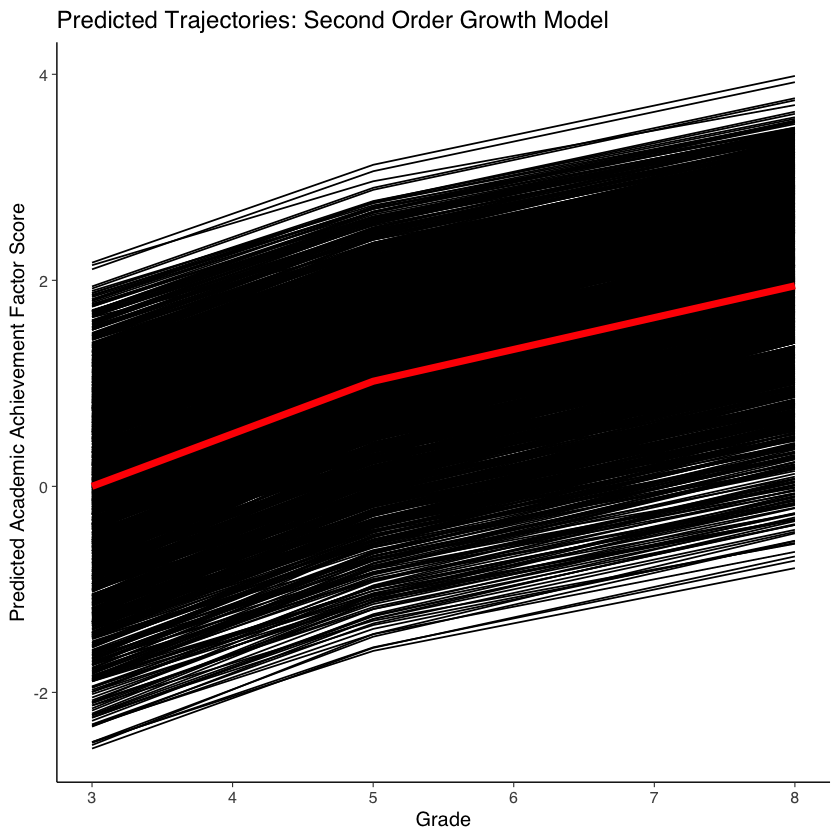
36.5. Traiettorie di sviluppo#
Possiamo visualizzare le traiettorie previste dei punteggi fattoriali nel modo seguente.
# extract predicted factor scores
pred <- as.data.frame(lavPredict(fit_growth))
# define function to fit factor trajectories
fit.line <- function(xi1, xi2, t) {
xi1 + xi2 * t
}
time <- c(0, .524, 1)
# fit trajectories using estimated factor scores
out <- NULL
temp <- NULL
for (i in 1:nrow(pred)) {
temp <- fit.line(pred$xi_1[i], pred$xi_2[i], time)
out <- rbind(out, temp)
}
out <- as.data.frame(out)
colnames(out) <- c("pred3", "pred5", "pred8")
out$ID <- dat$id
# reshape estimated scores to long format (for plotting)
outlong <- reshape(out,
varying = c("pred3", "pred5", "pred8"),
timevar = "grade",
idvar = "ID",
direction = "long", sep = ""
)
outlong <- outlong[order(outlong$ID, outlong$grade), ]
# fit average trajectory (for plotting)
avg <- as.data.frame(fit.line(0, 1.947, time))
avg$grade <- c(3, 5, 8)
avg$ID <- 1
colnames(avg) <- c("fit", "grade", "ID")
# plot predicted common factor trajectories (average in red)
ggplot(data = outlong, aes(x = grade, y = pred, group = ID)) +
ggtitle("Predicted Trajectories: Second Order Growth Model") +
xlab("Grade") +
ylab("Predicted Academic Achievement Factor Score") +
geom_line() +
geom_line(data = avg, aes(x = grade, y = fit, group = ID), color = "red", size = 2)
Warning message:
“Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
ℹ Please use `linewidth` instead.”
Warning message:
“Removed 1890 rows containing missing values (`geom_line()`).”
36.6. Conclusione#
Utilizzando più indicatori all’interno del framework di analisi dei fattori longitudinali, possiamo descrivere il cambiamento con maggiore precisione. Questo perché siamo in grado di filtrare il rumore di misura utilizzando un modello di misura multivariato. In questo modo, possiamo espandere le possibilità di indagine e studio delle differenze interindividuali nel cambiamento intra-individuale.
