34. Modelli di crescita latenti a gruppi multipli#
Nel capitolo precedente abbiamo esaminato i modelli di crescita con covariate invarianti nel tempo. Ora considereremo un quadro alternativo per esaminare le differenze tra le persone nel cambiamento: il confronto tra gruppi (McArdle, 1989; McArdle & Hamagami, 1996). I modelli di crescita con covariate invarianti nel tempo sono utili per studiare le differenze nelle traiettorie medie di crescita ma hanno una utilità limitata per esaminare le differenze in altri aspetti del processo di cambiamento intra-persona e le differenze tra le persone in quel processo. Senza estensione, tali modelli di covariate invarianti nel tempo non ci dicono nulla sulle differenze nelle varianze e covarianze tra i fattori di crescita, la variabilità residua e la struttura dei cambiamenti intra-persona. In questo capitolo illustriamo come il confronto tra gruppi possa essere utilizzato per esaminare le differenze in qualsiasi aspetto del modello di crescita. Questa flessibilità può fornire ulteriori informazioni su come e perché gli individui differiscono nel loro sviluppo.
Carichiamo i pacchetti necessari.
Per i nostri esempi, utilizziamo i punteggi di rendimento in matematica dai dati NLSY-CYA [si veda Grimm et al. [GRE16]]. Iniziamo a leggere i dati.
# set filepath for data file
filepath <- "https://raw.githubusercontent.com/LRI-2/Data/main/GrowthModeling/nlsy_math_long_R.dat"
# read in the text data file using the url() function
dat <- read.table(
file = url(filepath),
na.strings = "."
) # indicates the missing data designator
# copy data with new name
nlsy_math_long <- dat
# Add names the columns of the data set
names(nlsy_math_long) <- c(
"id", "female", "lb_wght",
"anti_k1", "math", "grade",
"occ", "age", "men",
"spring", "anti"
)
# reducing to variables of interest
nlsy_math_long <- nlsy_math_long[, c("id", "grade", "math", "lb_wght")]
# adding another dummy code variable for normal birth weight that coded the opposite of the low brithweight variable.
nlsy_math_long$nb_wght <- 1 - nlsy_math_long$lb_wght
# view the first few observations in the data set
head(nlsy_math_long, 10) |>
print()
id grade math lb_wght nb_wght
1 201 3 38 0 1
2 201 5 55 0 1
3 303 2 26 0 1
4 303 5 33 0 1
5 2702 2 56 0 1
6 2702 4 58 0 1
7 2702 8 80 0 1
8 4303 3 41 0 1
9 4303 4 58 0 1
10 5002 4 46 0 1
Esaminiamo le curve di crescita nei due gruppi.
# intraindividual change trajetories
ggplot(
data = nlsy_math_long, # data set
aes(x = grade, y = math, group = id)
) + # setting variables
geom_point(size = .5) + # adding points to plot
geom_line(alpha=0.3) + # adding lines to plot
# setting the x-axis with breaks and labels
scale_x_continuous(
limits = c(2, 8),
breaks = c(2, 3, 4, 5, 6, 7, 8),
name = "Grade at Testing"
) +
# setting the y-axis with limits breaks and labels
scale_y_continuous(
limits = c(10, 90),
breaks = c(10, 30, 50, 70, 90),
name = "PIAT Mathematics"
) +
facet_wrap(~lb_wght)
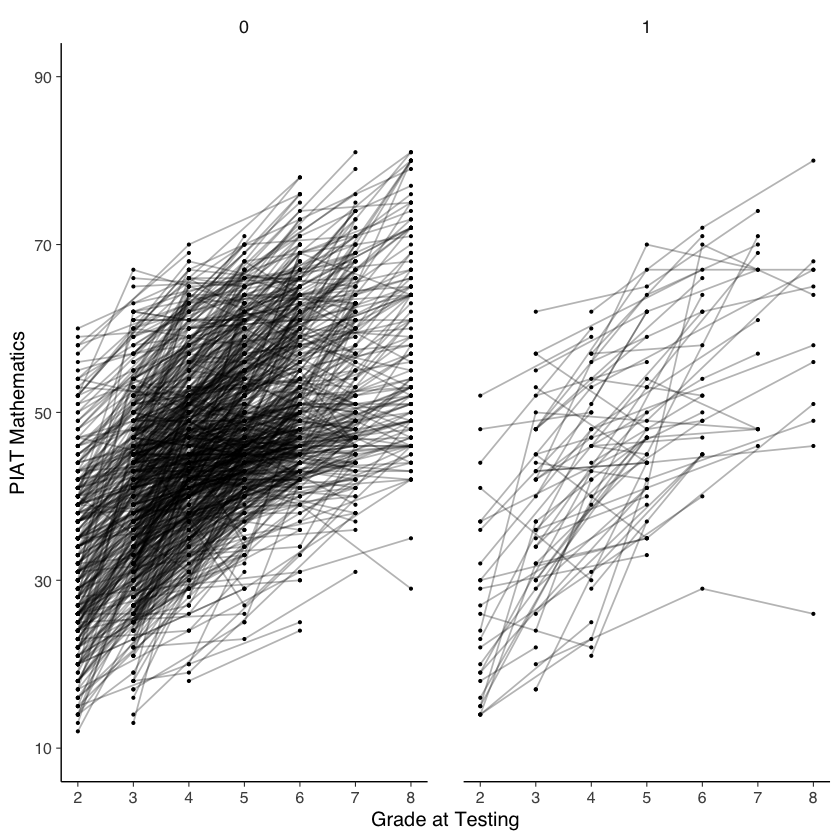
Per semplicità, carichiamo di nuovo i dati già trasformati in formato wide.
# set filepath for data file
filepath <- "https://raw.githubusercontent.com/LRI-2/Data/main/GrowthModeling/nlsy_math_wide_R.dat"
# read in the text data file using the url() function
dat <- read.table(
file = url(filepath),
na.strings = "."
) # indicates the missing data designator
# copy data with new name
nlsy_math_wide <- dat
# Give the variable names
names(nlsy_math_wide) <- c(
"id", "female", "lb_wght", "anti_k1",
"math2", "math3", "math4", "math5", "math6", "math7", "math8",
"age2", "age3", "age4", "age5", "age6", "age7", "age8",
"men2", "men3", "men4", "men5", "men6", "men7", "men8",
"spring2", "spring3", "spring4", "spring5", "spring6", "spring7", "spring8",
"anti2", "anti3", "anti4", "anti5", "anti6", "anti7", "anti8"
)
# view the first few observations (and columns) in the data set
head(nlsy_math_wide[, 1:11], 10)
| id | female | lb_wght | anti_k1 | math2 | math3 | math4 | math5 | math6 | math7 | math8 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | <int> | |
| 1 | 201 | 1 | 0 | 0 | NA | 38 | NA | 55 | NA | NA | NA |
| 2 | 303 | 1 | 0 | 1 | 26 | NA | NA | 33 | NA | NA | NA |
| 3 | 2702 | 0 | 0 | 0 | 56 | NA | 58 | NA | NA | NA | 80 |
| 4 | 4303 | 1 | 0 | 0 | NA | 41 | 58 | NA | NA | NA | NA |
| 5 | 5002 | 0 | 0 | 4 | NA | NA | 46 | NA | 54 | NA | 66 |
| 6 | 5005 | 1 | 0 | 0 | 35 | NA | 50 | NA | 60 | NA | 59 |
| 7 | 5701 | 0 | 0 | 2 | NA | 62 | 61 | NA | NA | NA | NA |
| 8 | 6102 | 0 | 0 | 0 | NA | NA | 55 | 67 | NA | 81 | NA |
| 9 | 6801 | 1 | 0 | 0 | NA | 54 | NA | 62 | NA | 66 | NA |
| 10 | 6802 | 0 | 0 | 0 | NA | 55 | NA | 66 | NA | 68 | NA |
34.1. Invarianza tra gruppi#
Definiamo il modello di crescita latente per i due gruppi.
# writing out linear growth model in full SEM way
mg_math_lavaan_model <- "
# latent variable definitions
#intercept (note intercept is a reserved term)
eta_1 =~ 1*math2
eta_1 =~ 1*math3
eta_1 =~ 1*math4
eta_1 =~ 1*math5
eta_1 =~ 1*math6
eta_1 =~ 1*math7
eta_1 =~ 1*math8
#linear slope
eta_2 =~ 0*math2
eta_2 =~ 1*math3
eta_2 =~ 2*math4
eta_2 =~ 3*math5
eta_2 =~ 4*math6
eta_2 =~ 5*math7
eta_2 =~ 6*math8
# factor variances
eta_1 ~~ eta_1
eta_2 ~~ eta_2
# covariances among factors
eta_1 ~~ eta_2
# factor means
eta_1 ~ start(35)*1
eta_2 ~ start(4)*1
# manifest variances (made equivalent by naming theta)
math2 ~~ theta*math2
math3 ~~ theta*math3
math4 ~~ theta*math4
math5 ~~ theta*math5
math6 ~~ theta*math6
math7 ~~ theta*math7
math8 ~~ theta*math8
# manifest means (fixed at zero)
math2 ~ 0*1
math3 ~ 0*1
math4 ~ 0*1
math5 ~ 0*1
math6 ~ 0*1
math7 ~ 0*1
math8 ~ 0*1
" # end of model definition
Adattiamo il modello ai dati specificando la separazione delle osservazioni in due gruppi e introducendo i vincoli di eguaglianza tra gruppi sulle saturazioni fattoriali, le medie, le varianze, le covarianze, e i residui. In questo modello, sostanzialmente, non c’è alcune differenza tra gruppi.
mg_math_lavaan_fitM1 <- sem(mg_math_lavaan_model,
data = nlsy_math_wide,
meanstructure = TRUE,
estimator = "ML",
missing = "fiml",
group = "lb_wght", # to separate groups
group.equal = c(
"loadings", # for constraints
"means",
"lv.variances",
"lv.covariances",
"residuals"
)
)
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING: some cases are empty and will be ignored:
741”
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING:
due to missing values, some pairwise combinations have less than
10% coverage; use lavInspect(fit, "coverage") to investigate.”
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING:
due to missing values, some pairwise combinations have 0%
coverage; use lavInspect(fit, "coverage") to investigate.”
Warning message in lav_mvnorm_missing_h1_estimate_moments(Y = X[[g]], wt = WT[[g]], :
“lavaan WARNING:
Maximum number of iterations reached when computing the sample
moments using EM; use the em.h1.iter.max= argument to increase the
number of iterations”
Warning message in lav_mvnorm_missing_h1_estimate_moments(Y = X[[g]], wt = WT[[g]], :
“lavaan WARNING:
Maximum number of iterations reached when computing the sample
moments using EM; use the em.h1.iter.max= argument to increase the
number of iterations”
Esaminiamo il risultato
summary(mg_math_lavaan_fitM1, fit.measures = TRUE) |>
print()
lavaan 0.6.15 ended normally after 24 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 24
Number of equality constraints 18
Number of observations per group: Used Total
0 857 858
1 75 75
Number of missing patterns per group:
0 60
1 25
Model Test User Model:
Test statistic 249.111
Degrees of freedom 64
P-value (Chi-square) 0.000
Test statistic for each group:
0 191.954
1 57.156
Model Test Baseline Model:
Test statistic 887.887
Degrees of freedom 42
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.781
Tucker-Lewis Index (TLI) 0.856
Robust Comparative Fit Index (CFI) 1.000
Robust Tucker-Lewis Index (TLI) 0.346
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -7968.693
Loglikelihood unrestricted model (H1) -7844.138
Akaike (AIC) 15949.386
Bayesian (BIC) 15978.410
Sample-size adjusted Bayesian (SABIC) 15959.354
Root Mean Square Error of Approximation:
RMSEA 0.079
90 Percent confidence interval - lower 0.069
90 Percent confidence interval - upper 0.089
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 0.436
Robust RMSEA 0.000
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.000
P-value H_0: Robust RMSEA <= 0.050 1.000
P-value H_0: Robust RMSEA >= 0.080 0.000
Standardized Root Mean Square Residual:
SRMR 0.128
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Group 1 [0]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta_1 =~
math2 1.000
math3 1.000
math4 1.000
math5 1.000
math6 1.000
math7 1.000
math8 1.000
eta_2 =~
math2 0.000
math3 1.000
math4 2.000
math5 3.000
math6 4.000
math7 5.000
math8 6.000
Covariances:
Estimate Std.Err z-value P(>|z|)
eta_1 ~~
eta_2 (.17.) -0.181 1.150 -0.158 0.875
Intercepts:
Estimate Std.Err z-value P(>|z|)
eta_1 (.18.) 35.267 0.355 99.229 0.000
eta_2 (.19.) 4.339 0.088 49.136 0.000
.math2 0.000
.math3 0.000
.math4 0.000
.math5 0.000
.math6 0.000
.math7 0.000
.math8 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
eta_1 (.15.) 64.562 5.659 11.408 0.000
eta_2 (.16.) 0.733 0.327 2.238 0.025
.math2 (thet) 36.230 1.867 19.410 0.000
.math3 (thet) 36.230 1.867 19.410 0.000
.math4 (thet) 36.230 1.867 19.410 0.000
.math5 (thet) 36.230 1.867 19.410 0.000
.math6 (thet) 36.230 1.867 19.410 0.000
.math7 (thet) 36.230 1.867 19.410 0.000
.math8 (thet) 36.230 1.867 19.410 0.000
Group 2 [1]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta_1 =~
math2 1.000
math3 1.000
math4 1.000
math5 1.000
math6 1.000
math7 1.000
math8 1.000
eta_2 =~
math2 0.000
math3 1.000
math4 2.000
math5 3.000
math6 4.000
math7 5.000
math8 6.000
Covariances:
Estimate Std.Err z-value P(>|z|)
eta_1 ~~
eta_2 (.17.) -0.181 1.150 -0.158 0.875
Intercepts:
Estimate Std.Err z-value P(>|z|)
eta_1 (.18.) 35.267 0.355 99.229 0.000
eta_2 (.19.) 4.339 0.088 49.136 0.000
.math2 0.000
.math3 0.000
.math4 0.000
.math5 0.000
.math6 0.000
.math7 0.000
.math8 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
eta_1 (.15.) 64.562 5.659 11.408 0.000
eta_2 (.16.) 0.733 0.327 2.238 0.025
.math2 (thet) 36.230 1.867 19.410 0.000
.math3 (thet) 36.230 1.867 19.410 0.000
.math4 (thet) 36.230 1.867 19.410 0.000
.math5 (thet) 36.230 1.867 19.410 0.000
.math6 (thet) 36.230 1.867 19.410 0.000
.math7 (thet) 36.230 1.867 19.410 0.000
.math8 (thet) 36.230 1.867 19.410 0.000
Creiamo il diagramma di percorso.
semPaths(mg_math_lavaan_fitM1, what = "path", whatLabels = "par")
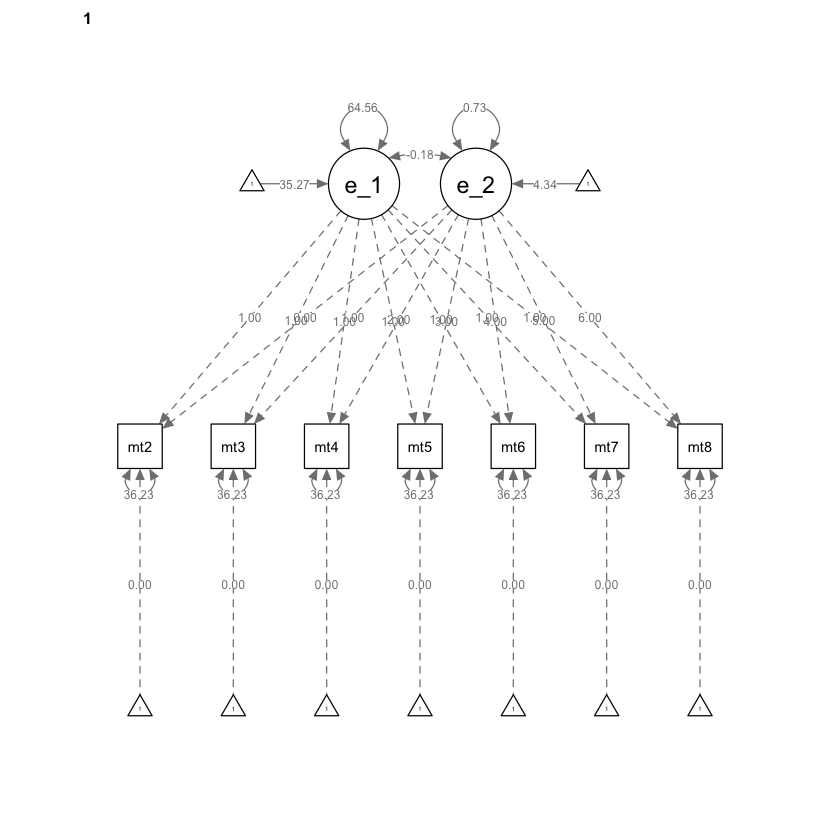
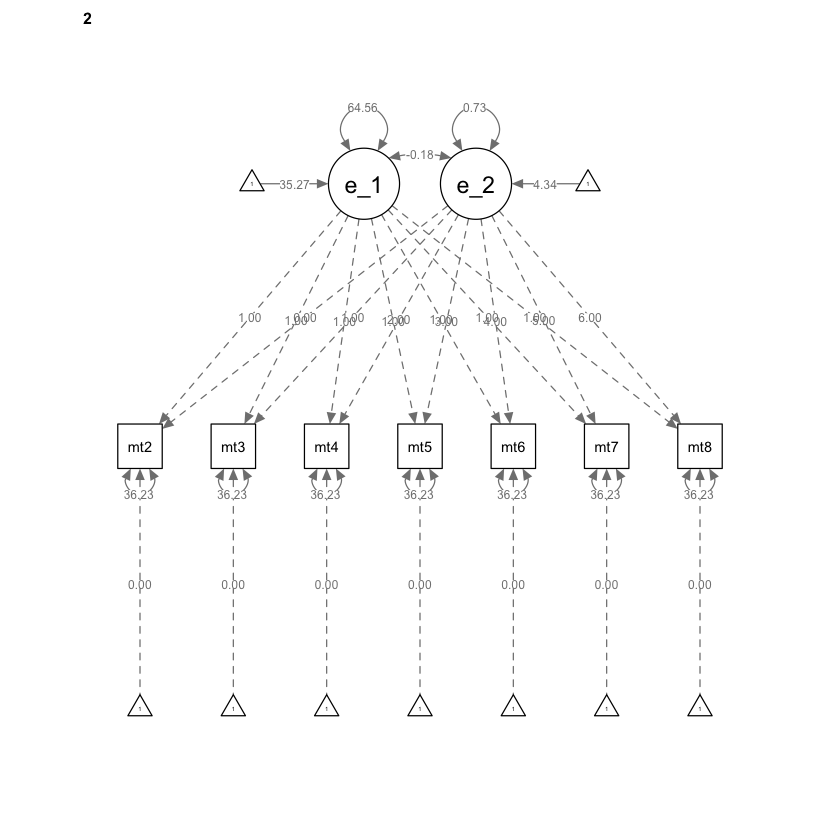
34.2. Vincoli sulle medie#
Trasformiamo ora il modello restrittivo specificato in precedenza allentando via via i vincoli che abbiamo introdotto. In questo modello rendiamo possibile la differenza tra le medie nei due gruppi.
mg_math_lavaan_fitM2 <- sem(mg_math_lavaan_model,
data = nlsy_math_wide,
meanstructure = TRUE,
estimator = "ML",
missing = "fiml",
group = "lb_wght", # to separate groups
group.equal = c(
"loadings", # for constraints
# "means", commented out so can differ
"lv.variances",
"lv.covariances",
"residuals"
)
)
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING: some cases are empty and will be ignored:
741”
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING:
due to missing values, some pairwise combinations have less than
10% coverage; use lavInspect(fit, "coverage") to investigate.”
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING:
due to missing values, some pairwise combinations have 0%
coverage; use lavInspect(fit, "coverage") to investigate.”
Warning message in lav_mvnorm_missing_h1_estimate_moments(Y = X[[g]], wt = WT[[g]], :
“lavaan WARNING:
Maximum number of iterations reached when computing the sample
moments using EM; use the em.h1.iter.max= argument to increase the
number of iterations”
Warning message in lav_mvnorm_missing_h1_estimate_moments(Y = X[[g]], wt = WT[[g]], :
“lavaan WARNING:
Maximum number of iterations reached when computing the sample
moments using EM; use the em.h1.iter.max= argument to increase the
number of iterations”
Esaminiamo il risultato.
summary(mg_math_lavaan_fitM2, fit.measures = TRUE) |>
print()
lavaan 0.6.15 ended normally after 31 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 24
Number of equality constraints 16
Number of observations per group: Used Total
0 857 858
1 75 75
Number of missing patterns per group:
0 60
1 25
Model Test User Model:
Test statistic 243.910
Degrees of freedom 62
P-value (Chi-square) 0.000
Test statistic for each group:
0 191.440
1 52.470
Model Test Baseline Model:
Test statistic 887.887
Degrees of freedom 42
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.785
Tucker-Lewis Index (TLI) 0.854
Robust Comparative Fit Index (CFI) 1.000
Robust Tucker-Lewis Index (TLI) 0.326
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -7966.093
Loglikelihood unrestricted model (H1) -7844.138
Akaike (AIC) 15948.185
Bayesian (BIC) 15986.884
Sample-size adjusted Bayesian (SABIC) 15961.477
Root Mean Square Error of Approximation:
RMSEA 0.079
90 Percent confidence interval - lower 0.069
90 Percent confidence interval - upper 0.090
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 0.472
Robust RMSEA 0.000
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.000
P-value H_0: Robust RMSEA <= 0.050 1.000
P-value H_0: Robust RMSEA >= 0.080 0.000
Standardized Root Mean Square Residual:
SRMR 0.127
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Group 1 [0]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta_1 =~
math2 1.000
math3 1.000
math4 1.000
math5 1.000
math6 1.000
math7 1.000
math8 1.000
eta_2 =~
math2 0.000
math3 1.000
math4 2.000
math5 3.000
math6 4.000
math7 5.000
math8 6.000
Covariances:
Estimate Std.Err z-value P(>|z|)
eta_1 ~~
eta_2 (.17.) -0.035 1.144 -0.031 0.975
Intercepts:
Estimate Std.Err z-value P(>|z|)
eta_1 35.488 0.369 96.080 0.000
eta_2 4.292 0.092 46.898 0.000
.math2 0.000
.math3 0.000
.math4 0.000
.math5 0.000
.math6 0.000
.math7 0.000
.math8 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
eta_1 (.15.) 63.704 5.637 11.301 0.000
eta_2 (.16.) 0.699 0.325 2.147 0.032
.math2 (thet) 36.321 1.871 19.413 0.000
.math3 (thet) 36.321 1.871 19.413 0.000
.math4 (thet) 36.321 1.871 19.413 0.000
.math5 (thet) 36.321 1.871 19.413 0.000
.math6 (thet) 36.321 1.871 19.413 0.000
.math7 (thet) 36.321 1.871 19.413 0.000
.math8 (thet) 36.321 1.871 19.413 0.000
Group 2 [1]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta_1 =~
math2 1.000
math3 1.000
math4 1.000
math5 1.000
math6 1.000
math7 1.000
math8 1.000
eta_2 =~
math2 0.000
math3 1.000
math4 2.000
math5 3.000
math6 4.000
math7 5.000
math8 6.000
Covariances:
Estimate Std.Err z-value P(>|z|)
eta_1 ~~
eta_2 (.17.) -0.035 1.144 -0.031 0.975
Intercepts:
Estimate Std.Err z-value P(>|z|)
eta_1 32.733 1.244 26.314 0.000
eta_2 4.905 0.320 15.320 0.000
.math2 0.000
.math3 0.000
.math4 0.000
.math5 0.000
.math6 0.000
.math7 0.000
.math8 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
eta_1 (.15.) 63.704 5.637 11.301 0.000
eta_2 (.16.) 0.699 0.325 2.147 0.032
.math2 (thet) 36.321 1.871 19.413 0.000
.math3 (thet) 36.321 1.871 19.413 0.000
.math4 (thet) 36.321 1.871 19.413 0.000
.math5 (thet) 36.321 1.871 19.413 0.000
.math6 (thet) 36.321 1.871 19.413 0.000
.math7 (thet) 36.321 1.871 19.413 0.000
.math8 (thet) 36.321 1.871 19.413 0.000
Eseguiamo il confronto tra i due modelli.
lavTestLRT(mg_math_lavaan_fitM1, mg_math_lavaan_fitM2) |>
print()
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff
mg_math_lavaan_fitM2 62 15948 15987 243.91
mg_math_lavaan_fitM1 64 15949 15978 249.11 5.2005 0.058601 2
Pr(>Chisq)
mg_math_lavaan_fitM2
mg_math_lavaan_fitM1 0.07425 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Non vi è evidenza che consentire una differenza tra medie tra gruppi migliori l’adattamento del modello.
34.3. Vincoli sulle varianze/covarianze#
Nel modello M3 consentiamo che anche le varianza e le covarianza differiscano tra gruppi, oltre alle medie.
mg_math_lavaan_fitM3 <- sem(mg_math_lavaan_model,
data = nlsy_math_wide,
meanstructure = TRUE,
estimator = "ML",
missing = "fiml",
group = "lb_wght", # to separate groups
group.equal = c(
"loadings", # for constraints
# "means", commented out so can differ
# "lv.variances",
# "lv.covariances",
"residuals"
)
)
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING: some cases are empty and will be ignored:
741”
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING:
due to missing values, some pairwise combinations have less than
10% coverage; use lavInspect(fit, "coverage") to investigate.”
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING:
due to missing values, some pairwise combinations have 0%
coverage; use lavInspect(fit, "coverage") to investigate.”
Warning message in lav_mvnorm_missing_h1_estimate_moments(Y = X[[g]], wt = WT[[g]], :
“lavaan WARNING:
Maximum number of iterations reached when computing the sample
moments using EM; use the em.h1.iter.max= argument to increase the
number of iterations”
Warning message in lav_mvnorm_missing_h1_estimate_moments(Y = X[[g]], wt = WT[[g]], :
“lavaan WARNING:
Maximum number of iterations reached when computing the sample
moments using EM; use the em.h1.iter.max= argument to increase the
number of iterations”
Esaminiamo i risultati.
summary(mg_math_lavaan_fitM3, fit.measures = TRUE) |>
print()
lavaan 0.6.15 ended normally after 57 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 24
Number of equality constraints 13
Number of observations per group: Used Total
0 857 858
1 75 75
Number of missing patterns per group:
0 60
1 25
Model Test User Model:
Test statistic 241.182
Degrees of freedom 59
P-value (Chi-square) 0.000
Test statistic for each group:
0 191.157
1 50.024
Model Test Baseline Model:
Test statistic 887.887
Degrees of freedom 42
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.785
Tucker-Lewis Index (TLI) 0.847
Robust Comparative Fit Index (CFI) 1.000
Robust Tucker-Lewis Index (TLI) 0.320
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -7964.728
Loglikelihood unrestricted model (H1) -7844.138
Akaike (AIC) 15951.457
Bayesian (BIC) 16004.668
Sample-size adjusted Bayesian (SABIC) 15969.732
Root Mean Square Error of Approximation:
RMSEA 0.081
90 Percent confidence interval - lower 0.071
90 Percent confidence interval - upper 0.092
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 0.598
Robust RMSEA 0.000
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.000
P-value H_0: Robust RMSEA <= 0.050 1.000
P-value H_0: Robust RMSEA >= 0.080 0.000
Standardized Root Mean Square Residual:
SRMR 0.124
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Group 1 [0]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta_1 =~
math2 1.000
math3 1.000
math4 1.000
math5 1.000
math6 1.000
math7 1.000
math8 1.000
eta_2 =~
math2 0.000
math3 1.000
math4 2.000
math5 3.000
math6 4.000
math7 5.000
math8 6.000
Covariances:
Estimate Std.Err z-value P(>|z|)
eta_1 ~~
eta_2 0.243 1.147 0.212 0.832
Intercepts:
Estimate Std.Err z-value P(>|z|)
eta_1 35.485 0.365 97.271 0.000
eta_2 4.293 0.091 47.089 0.000
.math2 0.000
.math3 0.000
.math4 0.000
.math5 0.000
.math6 0.000
.math7 0.000
.math8 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
eta_1 61.062 5.692 10.727 0.000
eta_2 0.663 0.326 2.033 0.042
.math2 (thet) 36.276 1.870 19.402 0.000
.math3 (thet) 36.276 1.870 19.402 0.000
.math4 (thet) 36.276 1.870 19.402 0.000
.math5 (thet) 36.276 1.870 19.402 0.000
.math6 (thet) 36.276 1.870 19.402 0.000
.math7 (thet) 36.276 1.870 19.402 0.000
.math8 (thet) 36.276 1.870 19.402 0.000
Group 2 [1]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta_1 =~
math2 1.000
math3 1.000
math4 1.000
math5 1.000
math6 1.000
math7 1.000
math8 1.000
eta_2 =~
math2 0.000
math3 1.000
math4 2.000
math5 3.000
math6 4.000
math7 5.000
math8 6.000
Covariances:
Estimate Std.Err z-value P(>|z|)
eta_1 ~~
eta_2 -3.801 4.912 -0.774 0.439
Intercepts:
Estimate Std.Err z-value P(>|z|)
eta_1 32.850 1.413 23.241 0.000
eta_2 4.881 0.341 14.332 0.000
.math2 0.000
.math3 0.000
.math4 0.000
.math5 0.000
.math6 0.000
.math7 0.000
.math8 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
eta_1 95.283 24.221 3.934 0.000
eta_2 1.297 1.315 0.986 0.324
.math2 (thet) 36.276 1.870 19.402 0.000
.math3 (thet) 36.276 1.870 19.402 0.000
.math4 (thet) 36.276 1.870 19.402 0.000
.math5 (thet) 36.276 1.870 19.402 0.000
.math6 (thet) 36.276 1.870 19.402 0.000
.math7 (thet) 36.276 1.870 19.402 0.000
.math8 (thet) 36.276 1.870 19.402 0.000
Confrontiamo il modello M2 con il modello M3.
lavTestLRT(mg_math_lavaan_fitM2, mg_math_lavaan_fitM3) |>
print()
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff Pr(>Chisq)
mg_math_lavaan_fitM3 59 15952 16005 241.18
mg_math_lavaan_fitM2 62 15948 15987 243.91 2.7283 0 3 0.4354
Non ci sono evidenze che una differenza nelle varianze e nelle covarianze tra gruppi migliori la bontà dell’adattamento del modello ai dati.
34.4. Vincoli sui residui#
Esaminiamo ora il vincolo sulle covarianze residue. Iniziamo a specificare il modello in una nuova forma.
mg_math_lavaan_model4 <- "
# latent variable definitions
#intercept (note intercept is a reserved term)
eta_1 =~ 1*math2
eta_1 =~ 1*math3
eta_1 =~ 1*math4
eta_1 =~ 1*math5
eta_1 =~ 1*math6
eta_1 =~ 1*math7
eta_1 =~ 1*math8
#linear slope
eta_2 =~ 0*math2
eta_2 =~ 1*math3
eta_2 =~ 2*math4
eta_2 =~ 3*math5
eta_2 =~ 4*math6
eta_2 =~ 5*math7
eta_2 =~ 6*math8
# factor variances
eta_1 ~~ start(60)*eta_1
eta_2 ~~ start(.75)*eta_2
# covariances among factors
eta_1 ~~ eta_2
# factor means
eta_1 ~ start(35)*1
eta_2 ~ start(4)*1
# manifest variances (made equivalent by naming theta)
math2 ~~ c(theta1,theta2)*math2
math3 ~~ c(theta1,theta2)*math3
math4 ~~ c(theta1,theta2)*math4
math5 ~~ c(theta1,theta2)*math5
math6 ~~ c(theta1,theta2)*math6
math7 ~~ c(theta1,theta2)*math7
math8 ~~ c(theta1,theta2)*math8
# manifest means (fixed at zero)
math2 ~ 0*1
math3 ~ 0*1
math4 ~ 0*1
math5 ~ 0*1
math6 ~ 0*1
math7 ~ 0*1
math8 ~ 0*1
" # end of model definition
Adattiamo il modello ai dati.
mg_math_lavaan_fitM4 <- sem(mg_math_lavaan_model4,
data = nlsy_math_wide,
meanstructure = TRUE,
estimator = "ML",
missing = "fiml",
group = "lb_wght", # to separate groups
group.equal = c("loadings")
) # for constraints
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING: some cases are empty and will be ignored:
741”
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING:
due to missing values, some pairwise combinations have less than
10% coverage; use lavInspect(fit, "coverage") to investigate.”
Warning message in lav_data_full(data = data, group = group, cluster = cluster, :
“lavaan WARNING:
due to missing values, some pairwise combinations have 0%
coverage; use lavInspect(fit, "coverage") to investigate.”
Warning message in lav_mvnorm_missing_h1_estimate_moments(Y = X[[g]], wt = WT[[g]], :
“lavaan WARNING:
Maximum number of iterations reached when computing the sample
moments using EM; use the em.h1.iter.max= argument to increase the
number of iterations”
Warning message in lav_mvnorm_missing_h1_estimate_moments(Y = X[[g]], wt = WT[[g]], :
“lavaan WARNING:
Maximum number of iterations reached when computing the sample
moments using EM; use the em.h1.iter.max= argument to increase the
number of iterations”
Warning message in lav_object_post_check(object):
“lavaan WARNING: some estimated lv variances are negative”
Esaminiamo i risulati.
summary(mg_math_lavaan_fitM4, fit.measures = TRUE) |>
print()
lavaan 0.6.15 ended normally after 62 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 24
Number of equality constraints 12
Number of observations per group: Used Total
0 857 858
1 75 75
Number of missing patterns per group:
0 60
1 25
Model Test User Model:
Test statistic 237.836
Degrees of freedom 58
P-value (Chi-square) 0.000
Test statistic for each group:
0 190.833
1 47.004
Model Test Baseline Model:
Test statistic 887.887
Degrees of freedom 42
P-value 0.000
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.787
Tucker-Lewis Index (TLI) 0.846
Robust Comparative Fit Index (CFI) 1.000
Robust Tucker-Lewis Index (TLI) 0.294
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -7963.056
Loglikelihood unrestricted model (H1) -7844.138
Akaike (AIC) 15950.111
Bayesian (BIC) 16008.159
Sample-size adjusted Bayesian (SABIC) 15970.048
Root Mean Square Error of Approximation:
RMSEA 0.082
90 Percent confidence interval - lower 0.071
90 Percent confidence interval - upper 0.092
P-value H_0: RMSEA <= 0.050 0.000
P-value H_0: RMSEA >= 0.080 0.607
Robust RMSEA 0.000
90 Percent confidence interval - lower 0.000
90 Percent confidence interval - upper 0.000
P-value H_0: Robust RMSEA <= 0.050 1.000
P-value H_0: Robust RMSEA >= 0.080 0.000
Standardized Root Mean Square Residual:
SRMR 0.124
Parameter Estimates:
Standard errors Standard
Information Observed
Observed information based on Hessian
Group 1 [0]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta_1 =~
math2 1.000
math3 1.000
math4 1.000
math5 1.000
math6 1.000
math7 1.000
math8 1.000
eta_2 =~
math2 0.000
math3 1.000
math4 2.000
math5 3.000
math6 4.000
math7 5.000
math8 6.000
Covariances:
Estimate Std.Err z-value P(>|z|)
eta_1 ~~
eta_2 -0.063 1.161 -0.054 0.957
Intercepts:
Estimate Std.Err z-value P(>|z|)
eta_1 35.481 0.365 97.257 0.000
eta_2 4.297 0.091 47.145 0.000
.math2 0.000
.math3 0.000
.math4 0.000
.math5 0.000
.math6 0.000
.math7 0.000
.math8 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
eta_1 62.287 5.728 10.873 0.000
eta_2 0.774 0.334 2.314 0.021
.math2 (tht1) 35.172 1.904 18.473 0.000
.math3 (tht1) 35.172 1.904 18.473 0.000
.math4 (tht1) 35.172 1.904 18.473 0.000
.math5 (tht1) 35.172 1.904 18.473 0.000
.math6 (tht1) 35.172 1.904 18.473 0.000
.math7 (tht1) 35.172 1.904 18.473 0.000
.math8 (tht1) 35.172 1.904 18.473 0.000
Group 2 [1]:
Latent Variables:
Estimate Std.Err z-value P(>|z|)
eta_1 =~
math2 1.000
math3 1.000
math4 1.000
math5 1.000
math6 1.000
math7 1.000
math8 1.000
eta_2 =~
math2 0.000
math3 1.000
math4 2.000
math5 3.000
math6 4.000
math7 5.000
math8 6.000
Covariances:
Estimate Std.Err z-value P(>|z|)
eta_1 ~~
eta_2 0.745 5.522 0.135 0.893
Intercepts:
Estimate Std.Err z-value P(>|z|)
eta_1 32.800 1.407 23.314 0.000
eta_2 4.873 0.341 14.298 0.000
.math2 0.000
.math3 0.000
.math4 0.000
.math5 0.000
.math6 0.000
.math7 0.000
.math8 0.000
Variances:
Estimate Std.Err z-value P(>|z|)
eta_1 79.627 25.629 3.107 0.002
eta_2 -0.157 1.477 -0.106 0.915
.math2 (tht2) 48.686 8.444 5.766 0.000
.math3 (tht2) 48.686 8.444 5.766 0.000
.math4 (tht2) 48.686 8.444 5.766 0.000
.math5 (tht2) 48.686 8.444 5.766 0.000
.math6 (tht2) 48.686 8.444 5.766 0.000
.math7 (tht2) 48.686 8.444 5.766 0.000
.math8 (tht2) 48.686 8.444 5.766 0.000
Facciamo un confronto tra la bontà di adattamento del modello M3 e del modello M4.
lavTestLRT(mg_math_lavaan_fitM3, mg_math_lavaan_fitM4) |>
print()
Chi-Squared Difference Test
Df AIC BIC Chisq Chisq diff RMSEA Df diff
mg_math_lavaan_fitM4 58 15950 16008 237.84
mg_math_lavaan_fitM3 59 15952 16005 241.18 3.3457 0.070948 1
Pr(>Chisq)
mg_math_lavaan_fitM4
mg_math_lavaan_fitM3 0.06738 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Anche in questo caso non otteniamo un risultato che fornisce evidenza di differenze tra i due gruppi.
34.5. Conclusioni#
In conclusione, possiamo dire che le evidenze presenti suggeriscono che i modelli di crescita latente per di due gruppi hanno parametri uguali per ciò che concerne le saturazioni fattoriali, le medie, le varianze, le covarianze e i residui.
