13. Attendibilità e modello fattoriale

In questo capitolo verrà affrontato il problema di misurare l’attendibilità di uno strumento usando la tecnica dell’analisi fattoriale. Verranno distinti tre diversi modelli che descrivono le relazioni tra gli indicatori e il fattore comune latente (modello congenerico, tau-equivalente, parallelo) e verranno forniti tre diversi indici per descrivere l’attendibilità quale coerenza interna, a seconda del modello ipotizzato: l’indice omega di McDonald, l’indice alpha di Cronbach e l’indice rho che deriva dalla formula “profetica” di Spearman-Brown. Vedremo che l’uso dell’indice alpha di Cronbach è giustificato solo se certe specifiche condizioni sono soddisfatte – e questo succede piuttosto raramente nei dati empirici. Per questa ragione, in generale, è più opportuno usare l’indice omega di McDonald quale misura di consistenza interna.

Un secondo tema importante che verrà affrontato sarà quello dell’uso del punteggio totale del test quale misura del costrutto latente. Questa è una pratica largamente usata, ma solo in parte giustificata. Esamineremo a questo proposito le considerazioni di McNeish e Wolf (2020).

13.1. Teoria classica dei test e analisi fattoriale

McDonald (2013) mostra come la teoria classica dei test possa essere messa in relazione con il modello dell’analisi fattoriale. La figura descrive nei termini del modello fattoriale la relazione che intercorre tra i punteggi \(Y\) ottenuti dalla somministrazione di un test con cinque item e i punteggi veri.

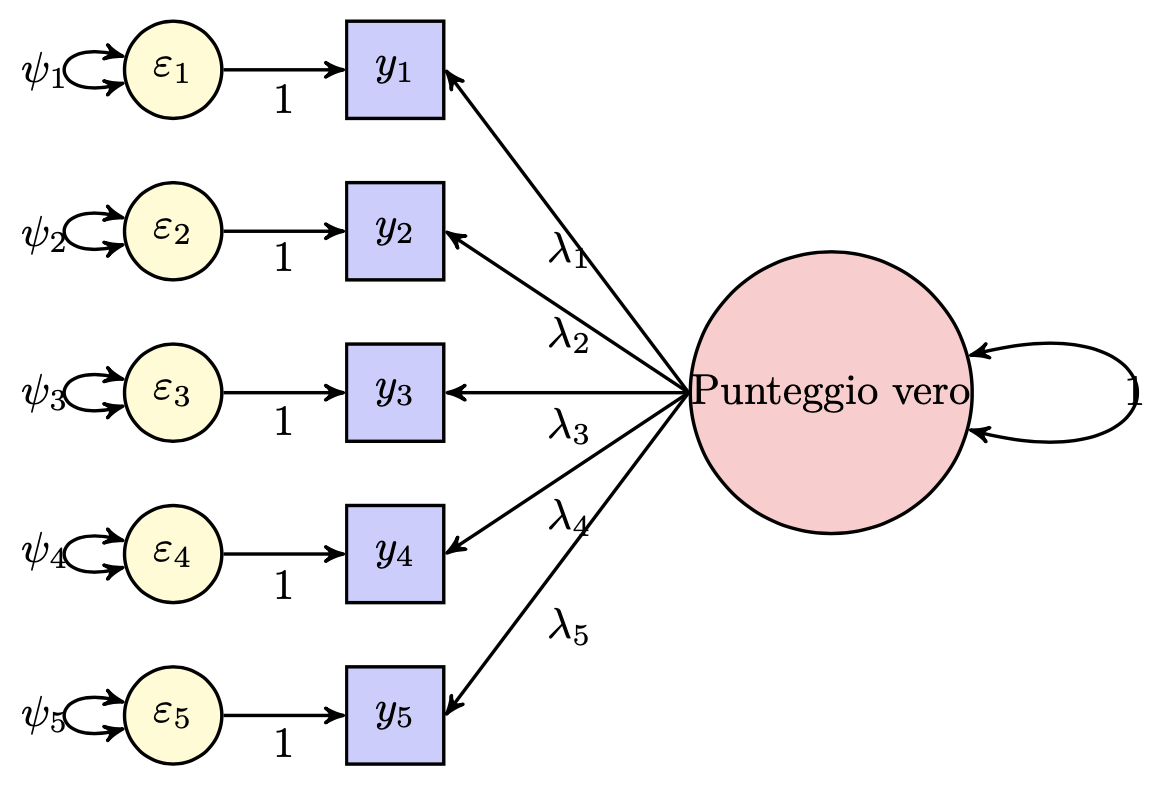
Fig. 13.1 Diagramma di percorso del modello monofattoriale.

Il metodo delle forme parallele proposto dalla teoria classica dei test fornisce una risposta solo in parte soddisfacente al problema della stima del coefficiente di attendibilità. Ricordiamo che il metodo delle forme parallele consiste nel somministrare due questionari \(X\) e \(X^\prime\), espressione dello stesso costrutto, nella stessa occasione allo stesso campione di soggetti. In tali circostanze \(\rho^2_{XT} = \rho_{XX^\prime}\). Affinché la relazione definita dall’equazione precedente sia vera, le due forme del test devono essere parallele, nel senso descritto della teoria classica dei test. In pratica, però, è impossibile somministrare lo stesso test due volte agli stessi rispondenti nelle medesime condizioni. È dunque necessario basare la stima del coefficiente di attendibilità sui dati acquisiti mediante un’unica somministrazione del test.

Vi sono vari metodi per la stima dell’attendibilità nel caso di un’unica somministrazione di un test. Considereremo qui tre metodi che possono essere applicati mediante l’utilizzo dell’analisi fattoriale: l’\(\alpha\) di Cronbach, l’\(\omega\) di McDonald e il metodo di Spearman-Brown. Il coefficiente \(\alpha\) è la misura più utilizzata per la stima dell’attendibilità quale coerenza interna, o omogeneità. Vedremo come tale indice costituisca il limite inferiore dell’attendibilità di un test, se alcune assunzioni sono soddisfatte, mentre risulta uno stimatore distorto dell’attendibilità se le assunzioni che descriveremo risultano violate.

Per discutere i diversi metodi di stima dell’attendibilità quale coerenza interna è prima necessario distinguere tra tre diverse forme che il modello mono-fattoriale può assumere. Queste tre forme sono quelle del modello con indicatori congenerici, \(\tau\)-equivalenti e paralleli.

13.2. Modello fattoriale e CTT

Sia \(X_1, X_2, \dots, X_p\), con \(p>2\), un insieme di item osservati. I punteggi ottenuti su tali item sono costituiti da una componente di punteggio vero e da una componente d’errore:

\[\begin{split} \begin{equation} \begin{aligned} X_1 &=T_1+E_1,\notag\\ X_2 &=T_2+E_2,\notag\\ &\dots\notag\\ X_p &=T_p+E_p.\notag \end{aligned} \end{equation} \end{split}\]

Seguendo McDonald (1999), tale scomposizione in una componente vera e in una componente d’errore può essere espressa nei termini dei parametri del modello fattoriale. L’espressione \(X_i = T_i + E_i\) può infatti essere riscritta come

\[ X_i = \lambda_i \xi + \delta_i, \quad{i=1, \dots, p}, \]

dove \(X_i\) denota il punteggio osservato per l’item \(i\)-esimo, \(\lambda_i\) è il peso fattoriale \(i\)-esimo, \(\xi\) è il fattore comune e \(\delta_i\) è la componente erratica del punteggio osservato \(i\)-esimo. Valgono le assunzioni del modello monofattoriale. Ovvero, si assume che \(\xi\) e \(\delta_i\) siano incorrelati per ciascun item \(i\)-esimo e che \(\delta_i\) e \(\delta_k\) siano incorrelati per ciascuna coppia \(i \neq k\).

13.3. Classi di modelli

Si possono distinguere tre importanti casi del modello mono-fattoriale:

• il modello con indicatori congenerici,

• il modello con indicatori \(\tau\)-equivalenti,

• il modello con indicatori paralleli.

Il modello con indicatori congenerici rappresenta il caso più generale, mentre gli indicatori \(\tau\)-equivalenti e paralleli sono casi particolari, ovvero impongono restrizioni al modello con indicatori congenerici.

13.3.1. Indicatori congenerici

Indicatori congenerici misurano lo stesso costrutto, ma non necessariamente nella stessa misura. Nel caso di indicatori congenerici, nel modello mono-fattoriale non viene imposto alcun vincolo né sulle saturazioni fattoriali né sulle specificità:

\[ \lambda_1\neq \lambda_2 \neq \dots\neq \lambda_p, \]

\[ \psi_{11}\neq \psi_{22} \neq \dots\neq \psi_{pp}. \]

Il modello mono-fattoriale con indicatori congenerici è dunque

(13.2)\[ \begin{equation} X_i = \lambda_i \xi + \delta_i. \end{equation} \]

Dalle assunzioni precedenti possiamo derivare la matrice \(\boldsymbol{\Sigma}\) riprodotta in base al modello congenerico la quale risulta essere uguale a

\[\begin{split} \boldsymbol{\Sigma}=\left[ \begin{array}{ c c c c } \sigma_{11} & \sigma_{12} & \dots & \sigma_{1p}, \\ \sigma_{21} & \sigma_{22} & \dots & \sigma_{2p}. \\ \vdots & \vdots & & \vdots\\ \sigma_{p1} & \sigma_{p2} & \dots & \sigma_{pp} \end{array} \right]. \end{split}\]

Si noti come tutte le varianze e tutte le covarianze siano tra loro diverse.

13.3.2. Indicatori tau-equivalenti

Nel caso di indicatori \(\tau\)-equivalenti, si ha che

\[ \lambda_1=\lambda_2=\dots=\lambda_p=\lambda, \]

\[ \psi_{11}\neq \psi_{22} \neq \dots\neq \psi_{pp}. \]

Il modello monofattoriale con indicatori \(\tau\)-equivalenti diventa dunque

(13.2)\[ \begin{equation} X_i = \lambda \xi + \delta_i, \end{equation} \]

ovvero

(13.3)\[ \begin{equation} X_i = \tau + \delta_i, \end{equation} \]

dove \(\tau=\lambda \xi\) è l’attributo comune scalato nell’unità di misura dell’indicatore. Secondo il modello (13.2), tutte le \(p(p-1)\) covarianze tra gli item del test devono essere uguali, ovvero

(13.4)\[ \begin{equation} \sigma_{ik} = \lambda^2=\sigma^2_T, \end{equation} \]

per \(i\neq k\). Gli elementi sulla diagonale principale della matrice di varianze e covarianze saranno invece

(13.5)\[ \begin{equation} \sigma_{ii} = \lambda^2 + \psi_{ii} =\sigma^2_T + \psi_{ii}. \end{equation} \]

La matrice \(\boldsymbol{\Sigma}\) riprodotta in base al modello \(\tau\)-equivalente è dunque uguale a

(13.6)\[\begin{split} \begin{equation} \boldsymbol{\Sigma}=\left[ \begin{array}{ c c c c } \sigma_{T}^2 + \psi_{11} & \sigma_{T}^2 & \dots & \sigma_{T}^2 \\ \sigma_{T}^2 & \sigma_{T}^2 + \psi_{22} & \dots & \sigma_{T}^2 \\ \vdots & \vdots & & \vdots\\ \sigma_{T}^2 & \sigma_{T}^2 & \dots & \sigma_{T}^2 + \psi_{pp} \end{array} \right]. \end{equation} \end{split}\]

Tutte le covarianze sono uguali, mentre le varianze sono tra loro diverse.

13.3.3. Indicatori paralleli

Nel caso di indicatori paralleli si ha che

\[ \lambda_1=\lambda_2=\dots=\lambda_p=\lambda, \]

\[ \psi_{11}=\psi_{22}=\dots=\psi_{pp}=\psi. \]

Il modello costituito da indicatori paralleli impone dunque un’ulteriore restrizione che riguarda le varianze degli item, ovvero:

\[ \sigma_{ii} = \lambda^2 + \psi =\sigma^2_T + \sigma^2. \]

La struttura di varianze e covarianze imposta dal modello per indicatori paralleli è dunque tale da richiedere l’uguaglianza tra tutte le covarianze tra gli item e l’uguaglianza tra tutte le varianze degli item. La matrice \(\boldsymbol{\Sigma}\) riprodotta in base al modello con indicatori paralleli è dunque uguale a

\[\begin{split} \boldsymbol{\Sigma}=\left[ \begin{array}{ c c c c } \sigma_{T}^2 + \sigma^2 & \sigma_{T}^2 & \dots & \sigma_{T}^2 \\ \sigma_{T}^2 & \sigma_{T}^2 + \sigma^2 & \dots & \sigma_{T}^2 \\ \vdots & \vdots & & \vdots\\ \sigma_{T}^2 & \sigma_{T}^2 & \dots & \sigma_{T}^2 +\sigma^2 \notag \end{array} \right]. \end{split}\]

13.3.4. Indicatori strettamente paralleli

L’aggiunta di un ulteriore vincolo a quelli definiti dal modello costituito da indicatori paralleli, ovvero quello dell’eguaglianza delle medie, definisce gli indicatori detti strettamente paralleli (McDonald, 1999).

13.4. Metodo dei minimi quadrati non pesati

Nel modello uni-fattoriale, la varianza di ciascun indicatore viene scomposta nella somma di due componenti: la componente \(\sigma^2_T\) dovuta all’effetto del fattore latente comune e la componente \(\psi\) dovuta all’effetto del fattore specifico. McDonald (2013) illustra come sia possibile stimare tali componenti dai dati osservati. Tali stime vengono poi utilizzate per calcolare la coerenza interna del test tramite le formule degli indici \(\alpha\) di Cronbach e \(\omega\) di McDonald.

In precedenza abbiamo visto come la varianza del punteggio vero sia uguale alla covarianza tra due forme parallele dello stesso test: \(\sigma^2_T = \sigma_{XX^\prime}\). Se gli indicatori sono \(\tau\)-equivalenti, la matrice la matrice \(\boldsymbol{\Sigma}\) riprodotta dal modello è uguale a

\[\begin{split} \boldsymbol{\Sigma}=\left[ \begin{array}{ c c c c } \sigma_{T}^2 + \psi_{11} & \sigma_{T}^2 & \dots & \sigma_{T}^2 \\ \sigma_{T}^2 & \sigma_{T}^2 + \psi_{22} & \dots & \sigma_{T}^2 \\ \vdots & \vdots & & \vdots\\ \sigma_{T}^2 & \sigma_{T}^2 & \dots & \sigma_{T}^2 + \psi_{pp} \notag \end{array} \right], \end{split}\]

ovvero, tutte le covarianze sono tra loro uguali. Nel caso di indicatori \(\tau\)-equivalenti, dunque, una stima \(\hat{\sigma}^2_T\) di \(\sigma^2_T\) è data dalla media delle covarianze della matrice S:

(13.7)\[ \begin{equation} \hat{\sigma}_T^2 = \frac{1}{p(p-1)} \sideset{}{} {\sum \sum}_{i \neq k} s_{ik}. \end{equation} \]

Tale medoto di stima di \(\sigma^2_T\) viene chiamato “metodo dei minimi quadrati non pesati” (McDonald, 2013).

Inoltre, nel caso di indicatori \(\tau\)-equivalenti, la stima di \(\psi_{ii}\) nella (13.5) è data da

\[ \hat{\psi}_{ii }= s_{ii} - \hat{\sigma}_T^2, \]

per ciascun item.

Nel caso di indicatori paralleli, la stima di \(\sigma^2_T\) è ancora data dalla (13.7), ovvero dalla media delle covarianze della matrice \(\boldsymbol{\Sigma}\). La stima del valore costante \(\psi\) è invece data da

(13.8)\[ \begin{equation} \hat{\psi} = \frac{1}{p} \sum_i (s_{ii} - \hat{\sigma}_T^2) \end{equation} \]

13.5. Varianza del punteggio totale di un test

Il punteggio totale \(Y\) di un test omogeneo è uguale alla somma dei punteggi \(X_i\) sui \(p\) item di cui è composto il test: \(Y = \sum_{i=1}^p X_i.\) Poniamoci ora il problema di descrivere la varianza del punteggio totale del test nei termini dei parametri del modello uni-fattoriale. Nel caso di un modello congenerico ad un fattore comune, la varianza del punteggio totale \(Y\) del test può essere scomposta in due componenti: il quadrato della somma delle saturazioni fattoriali, corrispondentente alla varianza attribuibile al punteggio vero (ovvero la quota di varianza derivante dall’attributo di cui gli item sono indicatori) e la somma delle varianze specifiche dei \(p\) indicatori, corrispondente alla varianza degli errori della misura del punteggio totale del test, ovvero

(13.9)\[ \begin{equation} \mathbb{V}(Y) = \left( \sum_i \lambda_i\right)^2 + \sum_i \psi_{ii} \end{equation} \]

Proof. Per un modello congenerico, la varianza del punteggio totale \(Y\) è uguale a:

\[\begin{split} \begin{equation} \begin{aligned} \mathbb{V}(Y) &= \mathbb{V}\left[ \sum_i \left(\lambda_i \xi + \delta_i\right) \right]\notag\\ &= \mathbb{V}\left[ (\lambda_1 \xi + \delta_1) + (\lambda_2 \xi + \delta_2) + \dots + (\lambda_p \xi + \delta_p) \right]\notag\\ &= \mathbb{V}\left[ \left( \sum_i \lambda_i\right) \xi + \sum_i \delta_i\right]\notag\\ &= \left(\sum_i \lambda_i\right)^2 \underbrace{\mathbb{V}(\xi)}_{=1} + \sum_i \mathbb{V}(\delta_i)\notag\\ &= \left(\sum_i \lambda_i\right)^2 + \sum_i \psi_{ii}.\notag \end{aligned} \end{equation} \end{split}\]

13.6. Stima dell’attendibilità

13.6.1. Coefficiente omega

Avendo scomposto la varianza del punteggio totale di un test come indicato nella (13.9)

\[ \mathbb{V}(Y) = \left( \sum_i \lambda_i\right)^2 + \sum_i \psi_{ii}. \]

McDonald (1999) definisce il coefficiente di attendibilità \(\omega\) come il rapporto tra la varianza “vera” (attribuibile all’attributo comune) e la varianza totale. Nei termini dei parametri del modello uni-fattoriale, il coefficiente \(\omega\) diventa:

(13.10)\[\begin{split} \begin{equation} \begin{aligned} \omega &= \frac{\left( \sum_{i=1}^p \lambda_i \right)^2}{\sigma_Y^2} \notag\\ &= \frac{\left( \sum_{i=1}^p \lambda_i \right)^2}{\left( \sum_{i=1}^p \lambda_i \right)^2 + \sum_{i=1}^p \psi_{ii}} \end{aligned} \end{equation} \end{split}\]

Il coefficiente \(\omega\) consente dunque di stimare il coefficiente di attendibilità nei termini dei parametri del modello fattoriale congenerico, utilizzando i dati ottenuti in un’unica somministrazione del test.

13.6.1.1. Un esempio concreto

Per illustrare la procedura per il calcolo del coefficiente \(\omega\), McDonald (1999) utilizza i dati derivanti dalla somministrazione del test Satisfaction With Life Scale (SWLS) a 215 rispondenti. Tale test è costituito da 14 item ma, per semplificare la discussione, McDonald ne utilizza solo 5.

SWLS <- matrix(
  c(
    2.565, 1.424, 1.481, 1.328, 1.529,
    1.424, 2.493, 1.267, 1.051, 1.308,
    1.481, 1.267, 2.462, 1.093, 1.360,
    1.328, 1.051, 1.093, 2.769, 1.128,
    1.529, 1.308, 1.360, 1.128, 3.355
  ),
  ncol = 5, byrow = TRUE
)
SWLS

A matrix: 5 × 5 of type dbl

2.565	1.424	1.481	1.328	1.529
1.424	2.493	1.267	1.051	1.308
1.481	1.267	2.462	1.093	1.360
1.328	1.051	1.093	2.769	1.128
1.529	1.308	1.360	1.128	3.355

Eseguiamo l’analisi fattoriale con il metodo della massima verosimiglianza:

fa <- factanal(covmat=SWLS, factors=1, n.obs=215)

Le saturazioni fattoriali sono:

fa$load

Loadings:
     Factor1
[1,] 0.817  
[2,] 0.694  
[3,] 0.726  
[4,] 0.591  
[5,] 0.643  

               Factor1
SS loadings      2.438
Proportion Var   0.488

Le specificità sono uguali a

fa$uniq

1. 0.333008655228646
2. 0.518170116026116
3. 0.473239886593545
4. 0.651215124917442
5. 0.586664002068541

Il coefficiente \(\omega\)

\[ \omega = \frac{\left( \sum_{i=1}^p \lambda_i \right)^2}{\left( \sum_{i=1}^p \lambda_i \right)^2 + \sum_{i=1}^p \psi_{ii}} \]

può essere calcolato nel modo seguente:

(sum(fa$load))^2 / (sum((fa$load))^2 + sum(fa$uniq))

0.824547701274471

Nel caso presente, il coefficiente di attendibilità \(\omega=0.82\) ci dice che l’\(82\)% della varianza del punteggio totale \(Y\) del test viene spiegato dal fattore comune latente.

13.6.1.2. Coefficiente \(\omega\) e assunzioni della teoria classica dei test

Il calcolo di \(\omega\) è basato sull’assunzione (tipica della teoria classica dei test) che \(\psi_{ik}=0\) per \(i\neq k\). Tale assunzione però potrebbe non essere soddisfatta nel caso di dati empirici. In tal caso, come indicato da Bollen (1980), la (13.10) diventa

(13.11)\[ \begin{equation} \omega = \frac{\left( \sum_{i=1}^p \lambda_i \right)^2}{\left( \sum_{i=1}^p \lambda_i \right)^2 + \sum_{i=1}^p \psi_{ii} + \sum_{i, k, i\neq k}^p \psi_{ik}}. \end{equation} \]

L’appropriatezza dell’assunzione dell’incorrelazione dei fattori specifici può essere verificata mediante un’analisi fattoriale confermativa. Se vi sono molte coppie di fattori specifici correlati, allora può essere necessario introdurre nel modello dei fattori aggiuntivi che rendano conto di queste covarianze. In questo caso, la scala non sarà più unidimensionale: la presenza di più fattori indica la presenza di più sottoscale. Il problema presentato sopra, tuttavia, non sempre può essere risolto individuando delle sottoscale perché, anche in tal caso, possono rimanere delle covarianze tra i fattori specifici che non sono spiegate dai fattori che individuano le sottoscale. In questi casi, per calcolare \(\omega\) sarà necessario utilizzare la eq:omega2.

McDonald (1999) attribuisce al coefficiente \(\omega\) le seguenti interpretazioni: \(\omega\) è uguale al quadrato della correlazione tra la \(Y\) e il fattore comune \(\xi\) o, in maniera equivalente, tra la \(Y\) e il punteggio vero (in base alla definizione di attendibilità: \(\rho_{XT}^2=\sigma^2_{\tau}/\sigma^2_X\)); \(\omega\) è uguale alla correlazione tra due test \(Y\) e \(Y'\) aventi la stessa somma (o media) delle saturazioni nel modello ad un fattore e la stessa somma (o media) delle varianze specifiche nel modello ad un fattore; \(\omega\) è uguale al quadrato della correlazione tra il punteggio totale di \(p\) item e il punteggio medio di un insieme infinito di item di un dominio omogeneo di cui i \(p\) item costituisciono un sottoinsieme.

13.6.2. Coefficiente \(\alpha\) di Cronbach

Il coefficiente \(\omega\) consente di stimare il coefficiente di attendibilità nel caso di un modello monofattoriale congenerico. Invece, il coefficiente \(\alpha\) fornisce una stima del coefficiente di attendibilità nel caso di un modello con indicatori \(\tau\)-equivalenti.

Se \(p\) item soddisfano il modello di \(\tau\)-equivalenza, la varianza di ciascun item può essere scomposta in una componente attribuibile al valore vero e in una componente d’errore, come indicato nella (13.5), ovvero, \(\sigma_{ii} = \lambda^2 + \psi_{ii} =\sigma^2_T + \sigma^2_i\). In base al principio di \(\tau\)-equivalenza, le varianze e covarianze riprodotte dal modello uni-fattoriale hanno le caratteristiche descritte nella matrice (13.6). Dato che tutti gli item hanno la stessa saturazione fattoriale \(\lambda\), la formula per il calcolo del coefficiente \(\omega\) si riduce a

\[ \omega = \frac{\left( \sum_i \lambda_i \right)^2}{\left( \sum_i \lambda_i \right)^2 + \sum_i \psi_{ii}} = \frac{p^2 \lambda^2}{\sigma^2_Y} = \frac{p^2 \sigma_T^2}{\sigma_Y^2} \]

dove \(Y\) è il punteggio totale del test.

Usando il metodo dei minimi quadrati non pesati, una stima di \(\omega\) può essere ottenuta nel modo seguente:

(13.12)\[ \begin{equation} \hat{\omega} = \frac{p^2 \hat{\sigma}_T^2}{s_Y^2} \end{equation} \]

dove una stima di \(\sigma_T^2\) viene fornita dalla (13.7), ovvero

(13.13)\[ \begin{equation} \hat{\sigma}_T^2 = \frac{1}{p(p-1)} \sideset{}{} {\sum \sum}_{i \neq k} s_{ik} \end{equation} \]

Inserendo la (13.13) nella (13.12), otteniamo

\[ \begin{equation} \hat{\omega} = \frac{p}{p-1}\frac{\sideset{}{} {\sum \sum}_{i \neq k} s_{ik}}{s_Y^2} \end{equation} \]

In conclusione, nel caso di indicatori \(\tau\)-eqivalenti, una stima del coefficiente \(\omega\) è data da

(13.14)\[\begin{split} \begin{equation} \begin{aligned} \hat{\omega} &= \frac{p}{p-1}\frac{\sideset{}{} {\sum \sum}_{i \neq k} s_{ik}}{s_Y^2} \notag\\ &= \frac{p}{p-1}\left(1-\frac{\sum_i s_{ii}}{s_Y^2}\right) \end{aligned} \end{equation} \end{split}\]

La stima dell’attendibilità fornita dalla (13.14) trova il suo corrispettivo per i valori della popolazione nell’equazione seguente:

(13.15)\[ \begin{equation} \begin{aligned} \alpha &= \frac{p}{p-1}\left(1-\frac{\sum_{i=1}^p \sigma_{ii}}{\sigma_Y^2}\right) &= \frac{p}{p-1}\frac{\sum_{i\neq k}^p \mbox{Cov}(X_i, X_k)}{\mathbb{V}(Y)} \end{aligned} \end{equation} \]

La (13.15) definisce quello che è conosciuto come il coefficiente \(\alpha\).

Il coefficiente \(\alpha\) fu scoperto da Guttman nel 1945 e incorrettamente attribuito a Cronbach. Viene spesso chiamato coefficiente \(\alpha\) di Guttman-Cronbach, o G-C \(\alpha\).

Se gli indicatori soddisfano i requisiti del modello di \(\tau\)-equivalenza, i coefficienti \(\alpha\) e \(\omega\) sono uguali. Se il modello di \(\tau\)-equivalenza è appropriato, il coefficiente \(\alpha\) fornisce un limite inferiore del coefficiente \(\omega\) (ovvero, fornisce una sottostima di \(\omega\)): \(\omega \geq \alpha\). A causa del fatto che fornisce una stima conservativa del coefficiente di attendibilità, \(\alpha\) viene preferito ad \(\omega\) da alcuni ricercatori. Si noti però che \(\alpha\) possiede tale carattere conservativo solo nel caso in cui le assunzioni del modello \(\tau\)-equivalente siano soddisfatte.

13.6.2.1. Un esempio concreto

consideriamo nuovamente la matrice di varianze e covarianze SWLS. Il coefficiente \(\alpha\) si calcola usando la (13.14) e, per i dati presenti, risulta essere uguale a

p <- 5
alpha <- (p / (p - 1)) * (1 - tr(SWLS) / sum(SWLS))
alpha

0.81912232833106

Lo stesso risultato si ottiene utilizzando la funzione alpha() contenuta nel pacchetto psych:

alpha(SWLS)

Reliability analysis   
Call: alpha(x = SWLS)

  raw_alpha std.alpha G6(smc) average_r S/N median_r
      0.82      0.82    0.79      0.48 4.6     0.49

    95% confidence boundaries 
      lower alpha upper
Feldt  0.33  0.82  0.98

 Reliability if an item is dropped:
   raw_alpha std.alpha G6(smc) average_r S/N  var.r med.r
V1      0.75      0.76    0.70      0.44 3.1 0.0027  0.44
V2      0.78      0.79    0.74      0.48 3.7 0.0060  0.49
V3      0.78      0.78    0.73      0.47 3.5 0.0055  0.48
V4      0.81      0.81    0.77      0.52 4.3 0.0027  0.52
V5      0.80      0.80    0.75      0.50 3.9 0.0057  0.50

 Item statistics 
      r r.cor r.drop
V1 0.83  0.79   0.71
V2 0.77  0.68   0.62
V3 0.78  0.71   0.64
V4 0.70  0.58   0.53
V5 0.74  0.63   0.57

13.6.2.2. Violazione dell’assunto di tau-equivalenza {#sec:violazione_tau}

Il coefficiente \(\alpha\), la misura di attendibilità maggiormente usata in psicometria, è basato sull’assuzione che il modello di misurazione sia \(\tau\)-equivalente. Come indicato sopra, se tale assunzione è soddisfatta, \(\alpha\) fornisce un limite inferiore dell’attendibilità del test. Nei casi in cui tale assunzione venga violata, però, \(\alpha\) può perdere tale carattere conservativo e può fornire una sovrastima dell’attendibilità del test (Sijtsma, 2009).

NKano e Azuma (2003) riportano i risultati di una simulazione che mette in evidenza le conseguenze che risultano dalla violazione dell’assunzione di incorrelazione tra le componenti specifiche del modello monofattoriale. Questi autori trovano che, quando il principio dell’incorrelazione dei fattori specifici è violato, allora le stime dell’attendibilità ottenute mediante il coefficiente \(\alpha\) sono affette da un errore sistematico. Tale errore sistematico aumenta all’aumentare del numero di coppie di fattori specifici che risultano tra loro correlati. In queste circostanze, dunque, il coefficiente \(\alpha\) non fornisce più una stima conservativa dell’attendibilità.

In conclusione, il coefficiente \(\omega\) fornisce una stima adeguata dell’attendibilità nel caso di un modello di misurazione congenerico. L’utilizzo del coefficiente \(\alpha\) per la stima dell’attendibilità richiede un modello di misurazione \(\tau\)-equivalente. L’esistenza di fattori specifici correlati invalida sia il coefficiente \(\alpha\), sia il coefficiente \(\omega\) calcolato in base alla eq:omega. In tali circostanze l’attendibilità deve essere stimata utilizzando una diversa equazione (Kano & Azuma, 2003; Komaroff, 1997).

Questa discussione mette in evidenza un aspetto importante: il coefficiente \(\alpha\) fornisce una stima conservativa dell’attendibilità di un test solo se le variabili osservate sono associate alle variabili latenti come indicato dal modello di misurazione \(\tau\)-equivalente. Se le assunzioni del modello \(\tau\)-equivalente sono violate (per esempio, l’assunzione dell’incorrelazione degli errori), allora \(\alpha\) porta ad una sovrastima stima dell’attendibilità del test.

Sijtsma (2009), tra gli altri, sconsiglia l’uso di \(\alpha\) per la stima dell’attendibilità del test in quanto, nelle applicazioni reali, le assunzioni di \(\tau\)-equivalenza e dell’incorrelazione degli errori risultano spesso violate. La violazione dell’assunzione di \(\tau\)-equivalenza porta ad una stima conservativa dell’attendibilità, mentre la violazione dell’assunzione dell’incorrelazione degli errori porta ad una stima liberale dell’attendibilità. In entrambi i casi, l’errore sistematico può essere sostanziale.

Un secondo problema è che \(\alpha\) viene spesso preso quale misura della “struttura interna” di un test e quindi come evidenza che gli item del test “misurino la stessa cosa.” Tale interpretazione di \(\alpha\) è sbagliata, in quanto \(\alpha\) non fornisce alcuna informazione a questo proposito. Non è semplice fornire ad \(\alpha\) una chiara interpretazione, anche nel caso in cui siano soddisfatte le assunzioni del modello di misurazione su cui si basa.

13.6.3. La formula “profetica” di Spearman-Brown

La formula “profetica” di Spearman-Brown viene usata per misurare l’attendibilità nel caso di un modello di misurazione costituito da indicatori paralleli. Si considerino \(p\) item paralleli, tali per cui \(\lambda_1=\lambda_2=\dots=\lambda_p=\lambda\) e \(\psi_{11}=\psi_{22}=\dots=\psi_{pp}=\psi\). In tal caso, la quota di varianza del punteggio totale del test che viene spiegata dalla variabile latente è uguale a

\[ \left(\sum_i \lambda_i \right)^2 = (p \lambda)^2 = p^2 \lambda^2. \]

L’attendibilità di un singolo item, che chiamerò \(\rho_1\), è data da

\[ \rho_1 = \frac{\sigma_T^2}{\sigma_T^2+ \sigma_E^2} = \frac{\lambda^2}{\lambda^2 + \psi}. \]

Per \(p\) item paralleli avremo che

\[\begin{split} \begin{equation} \begin{aligned} \rho_p &= \frac{p^2 \lambda^2}{p^2 \lambda^2 + p \psi} \notag\\ &= \frac{p^2 \lambda^2}{ p (p \lambda^2 + \psi)} \notag\\ &= \frac{p \lambda^2}{ p \lambda^2 + \psi} \notag\\ &= \frac{p \lambda^2}{(p-1) \lambda^2 + (\lambda^2 + \psi)}. \notag \end{aligned} \end{equation} \end{split}\]

Ricordando che l’attendibilità di ciascun singolo item è \(\rho_1 = \frac{\lambda^2}{\lambda^2 + \psi}\), abbiamo che

(13.16)\[\begin{split} \begin{equation} \begin{aligned} \rho_p &= \frac{p \frac{\lambda^2}{\lambda^2+\psi}}{(p-1) \frac{\lambda^2}{\lambda^2+\psi} + \frac{\lambda^2 + \psi}{\lambda^2+\psi}} \notag\\ &= \frac{p \rho_1}{(p-1)\rho_1 + 1}. \end{aligned} \end{equation} \end{split}\]

La eq:spearman-brown-der esprime l’attendibilità \(\rho_p\) di un test costituito da \(p\) item paralleli come funzione dell’attendibilità che caratterizza un singolo item. La eq:spearman-brown-der è tradizionalmente conosciuta con il nome di formula “profetica” di Spearman-Brown (Spearman-Brown prophecy formula). Nel caso di item paralleli si ha che

\[ \omega=\alpha=\rho_p. \]

13.6.3.1. Un esempio concreto

Poniamoci il problema di calcolare l’attendibilità del test SWLS utilizzando la formula di Spearman-Brown. Ipotizziamo dunque che gli item della scala SWLS siano paralleli. La matrice di correlazione è:

R <- cov2cor(SWLS)
round(R, 3)

A matrix: 5 × 5 of type dbl

1.000	0.563	0.589	0.498	0.521
0.563	1.000	0.511	0.400	0.452
0.589	0.511	1.000	0.419	0.473
0.498	0.400	0.419	1.000	0.370
0.521	0.452	0.473	0.370	1.000

Seguendo McDonald [McD13], supponiamo di calcolare l’attendibilità di un singolo item (\(\rho_1\)) come la correlazione media tra gli item:

rr <- NULL
p <- 5
k <- 1
for (i in 1:p) {
  for (j in 1:p) {
    if (j != i) {
      rr[k] <- R[i, j]
    }
    k <- k + 1
  }
}
ro_1 <- mean(rr, na.rm = TRUE)
ro_1

0.479759331457527

Applicando la formula di Spearman-Brown, la stima dell’attendibilità del test diventa pari a

(p * ro_1) / ((p - 1) * ro_1 + 1)

0.821776630281859

13.7. Punteggio totale e modello fattoriale parallelo

McNeish e Wolf (2020) richiamano l’attenzione sul fatto che usare il punteggio totale quale misura di un costrutto è possibile solo quando i dati soddisfano i vincoli di un modello fattoriale parallelo.

Consideriamo l’esempio seguente, nel quale McNeish e Wolf (2020) esaminano i dati “classici” di Holzinger and Swineford (1939), i quali si riferiscono ai seguenti item:

• Paragraph comprehension

• Sentence completion

• Word definitions

• Speeded addition

• Speeded dot counting

• Discrimination between curved and straight letters

Leggiamo i dati in R.

d <- rio::import(
  "data/1_Factor_Parallel.csv"
)

McNeish e Wolf (2020) sottolineano il fatto che il punteggio totale

\[ \text{Punteggio totale} = \text{Item 1 + Item 2 + Item 3 + Item 4 + Item 5 + Item 6} \]

rappresenta l’idea che ciasun item fornisca la stessa quantità di informazione relativamente alla misura del costrutto. Ciò può essere specificato da un modello fattoriale nel quale le saturazioni fattoriali degli item sono tutte uguali a 1. Questo corrisponde al modello parallelo che abbiamo discusso in precedenza. In tali circostanze, i punteggi fattoriali del test risultano perfettamente associati al punteggio totale (correlazione uguale a 1). Dunque, se tale modello fattoriale è giustificato dai dati, questo giustifica l’uso del punteggio totale del test quale misura del costrutto.

È facile verificare tali affermazioni. Implementiamo il modello parallelo.

m_parallel <-
  "
  # all loadings are fixed to one
  f1 =~ 1*X4 + 1*X5 + 1*X6 + 1*X7 + 1*X8 + 1*X9
  
  # all residual variances constrained to same value
  X4 ~~ theta*X4
  X5 ~~ theta*X5
  X6 ~~ theta*X6
  X7 ~~ theta*X7
  X8 ~~ theta*X8
  X9 ~~ theta*X9
"

Adattiamo il modello parallelo ai dati forniti dagli autori.

fit_parallel <- sem(m_parallel, data=d)

Calcoliamo il punteggio totale.

d$ts <- with(
  d,
  X4 + X5 + X6 + X7 + X8 + X9
)

Calcoliamo i punteggi fattoriali.

scores <- lavPredict(fit_parallel, method="regression")
d$scores <- as.numeric(scores)

Un diagramma a dispersione tra il punteggio totale e i punteggi fattoriali conferma che i due sono perfettamente associati. Quindi, usare il punteggio totale o i punteggi fattoriali è equivalente.

d |> 
  ggplot(aes(x=ts, y=scores)) + 
  geom_point()

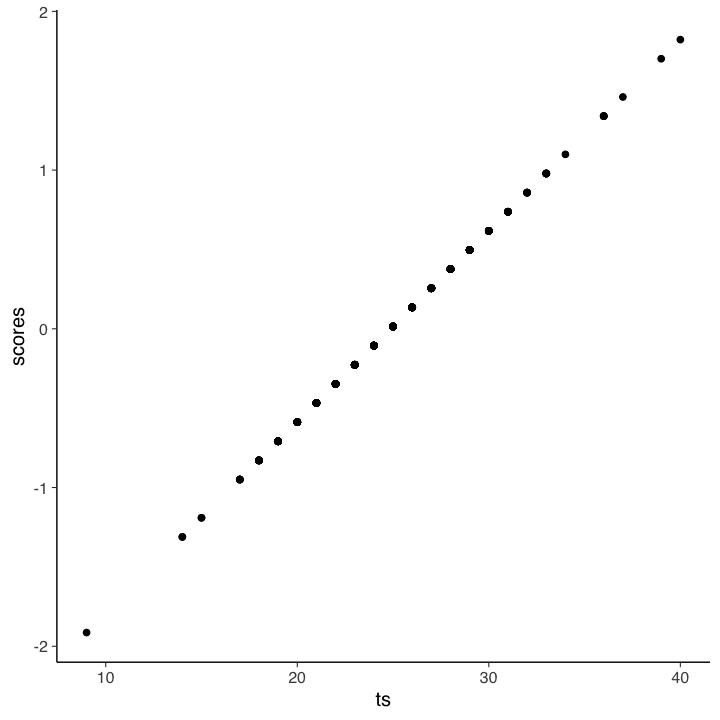
Tuttavia, questa conclusione è valida solo se il modello parallelo è giustificato per i dati. Se esaminiamo l’output di lavaan vediamo che, nel caso presente, questo non è vero.

# report output with fit measures and standardized estimates
out = summary(fit_parallel, fit.measures = TRUE, standardized = TRUE)
print(out)

lavaan 0.6.15 ended normally after 13 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                         7
  Number of equality constraints                     5

  Number of observations                           301

Model Test User Model:
                                                      
  Test statistic                               325.899
  Degrees of freedom                                19
  P-value (Chi-square)                           0.000

Model Test Baseline Model:

  Test statistic                               568.519
  Degrees of freedom                                15
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.446
  Tucker-Lewis Index (TLI)                       0.562

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -2680.931
  Loglikelihood unrestricted model (H1)      -2517.981
                                                      
  Akaike (AIC)                                5365.862
  Bayesian (BIC)                              5373.276
  Sample-size adjusted Bayesian (SABIC)       5366.933

Root Mean Square Error of Approximation:

  RMSEA                                          0.232
  90 Percent confidence interval - lower         0.210
  90 Percent confidence interval - upper         0.254
  P-value H_0: RMSEA <= 0.050                    0.000
  P-value H_0: RMSEA >= 0.080                    1.000

Standardized Root Mean Square Residual:

  SRMR                                           0.206

Parameter Estimates:

  Standard errors                             Standard
  Information                                 Expected
  Information saturated (h1) model          Structured

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  f1 =~                                                                 
    X4                1.000                               0.633    0.551
    X5                1.000                               0.633    0.551
    X6                1.000                               0.633    0.551
    X7                1.000                               0.633    0.551
    X8                1.000                               0.633    0.551
    X9                1.000                               0.633    0.551

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .X4      (thet)    0.920    0.034   27.432    0.000    0.920    0.697
   .X5      (thet)    0.920    0.034   27.432    0.000    0.920    0.697
   .X6      (thet)    0.920    0.034   27.432    0.000    0.920    0.697
   .X7      (thet)    0.920    0.034   27.432    0.000    0.920    0.697
   .X8      (thet)    0.920    0.034   27.432    0.000    0.920    0.697
   .X9      (thet)    0.920    0.034   27.432    0.000    0.920    0.697
    f1                0.400    0.045    8.803    0.000    1.000    1.000

Dunque, per questi dati, il punteggio totale può ovviamente essere calcolato. Ma non fornisce una misura adeguata del costrutto. Dunque, il punteggio totale non dovrebbe essere usato nel caso dei dati ottenuti con questo test.

Gli autori adattano ai dati un modello congenerico.

m_congeneric <- 
'
  #all loadings are uniquely estimated
  f1 =~ NA*X4 + X5 + X6 + X7 + X8 + X9
  #constrain factor variance to 1
  f1 ~~ 1*f1
'

# Fit above model
fit_congeneric <- sem(m_congeneric, data=d)

parameterEstimates(fit_congeneric, standardized = TRUE) %>%
  dplyr::filter(op == "=~") %>%
  dplyr::select(
    "Latent Factor" = lhs,
    Indicator = rhs,
    B = est,
    SE = se,
    Z = z,
    "p-value" = pvalue,
    Beta = std.all
  ) %>%
  knitr::kable(
    digits = 3, booktabs = TRUE, format = "markdown",
    caption = "Factor Loadings"
  )

Table: Factor Loadings

|Latent Factor |Indicator |     B|    SE|      Z| p-value|  Beta|
|:-------------|:---------|-----:|-----:|------:|-------:|-----:|
|f1            |X4        | 0.963| 0.059| 16.274|   0.000| 0.824|
|f1            |X5        | 1.121| 0.067| 16.835|   0.000| 0.846|
|f1            |X6        | 0.894| 0.058| 15.450|   0.000| 0.792|
|f1            |X7        | 0.195| 0.071|  2.767|   0.006| 0.170|
|f1            |X8        | 0.185| 0.063|  2.938|   0.003| 0.180|
|f1            |X9        | 0.278| 0.065|  4.245|   0.000| 0.258|

Si noti che le saturazioni fattoriali standardizzate sono molto diverse tra loro, suggerendo che il punteggio del costrutto si relaziona in modo diverso con ciascun item e che sarebbe inappropriato stimare il punteggio del costrutto assegnando un peso unitario agli item.

McNeish e Wolf (2020) calcolano poi i punteggi fattoriali del modello congenerico.

scores_cong <- lavPredict(fit_congeneric, method="regression")
d$scores_cong <- as.numeric(scores_cong)

Il grafico seguente mostra la relazione tra i punteggi fattoriali e il punteggio totale.

d |> 
  ggplot(aes(x=ts, y=scores_cong)) + 
  geom_point()

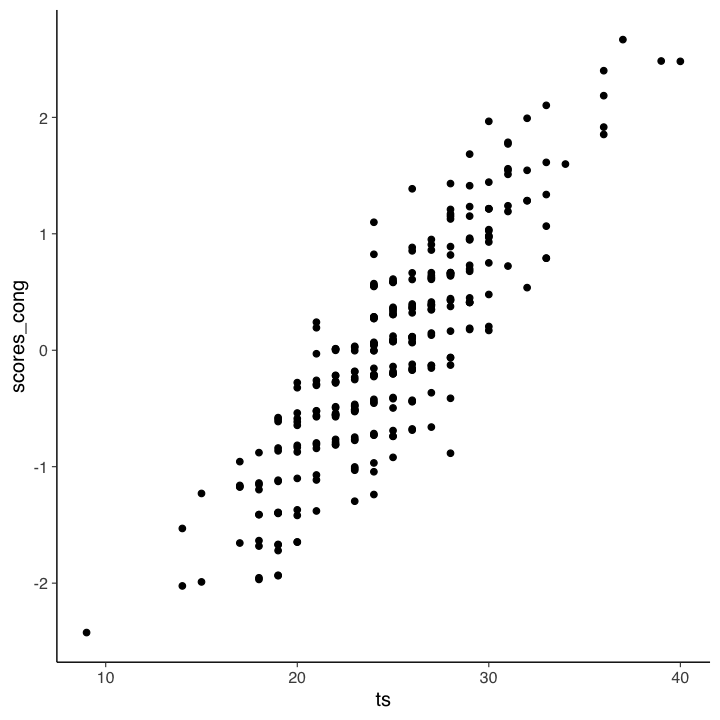
Nel caso presente, il coefficiente di determinazione tra punteggio totale e punteggi fattoriali è 0.77.

cor(d$ts, d$scores_cong)^2

0.765992021080727

Secondo gli autori, ciò significa che due persone con un punteggio totale identico potrebbero avere punteggi di modello congenerico potenzialmente diversi perché hanno raggiunto il loro particolare punteggio totale approvando item diversi. Poiché il modello congenerico assegna pesi diversi agli item, ciascun item contribuisce in modo diverso al punteggio fattoriale del modello congenerico, il che non è vero per il punteggio totale.

Si noti che, per i dati di Holzinger and Swineford (1939), neppure un modello congenerico ad un fattore si dimostra adeguato.

out = summary(fit_congeneric, fit.measures = TRUE, standardized = TRUE)
print(out)

lavaan 0.6.15 ended normally after 16 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        12

  Number of observations                           301

Model Test User Model:
                                                      
  Test statistic                               115.366
  Degrees of freedom                                 9
  P-value (Chi-square)                           0.000

Model Test Baseline Model:

  Test statistic                               568.519
  Degrees of freedom                                15
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.808
  Tucker-Lewis Index (TLI)                       0.680

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -2575.664
  Loglikelihood unrestricted model (H1)      -2517.981
                                                      
  Akaike (AIC)                                5175.328
  Bayesian (BIC)                              5219.813
  Sample-size adjusted Bayesian (SABIC)       5181.756

Root Mean Square Error of Approximation:

  RMSEA                                          0.198
  90 Percent confidence interval - lower         0.167
  90 Percent confidence interval - upper         0.231
  P-value H_0: RMSEA <= 0.050                    0.000
  P-value H_0: RMSEA >= 0.080                    1.000

Standardized Root Mean Square Residual:

  SRMR                                           0.129

Parameter Estimates:

  Standard errors                             Standard
  Information                                 Expected
  Information saturated (h1) model          Structured

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  f1 =~                                                                 
    X4                0.963    0.059   16.274    0.000    0.963    0.824
    X5                1.121    0.067   16.835    0.000    1.121    0.846
    X6                0.894    0.058   15.450    0.000    0.894    0.792
    X7                0.195    0.071    2.767    0.006    0.195    0.170
    X8                0.185    0.063    2.938    0.003    0.185    0.180
    X9                0.278    0.065    4.245    0.000    0.278    0.258

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    f1                1.000                               1.000    1.000
   .X4                0.437    0.056    7.775    0.000    0.437    0.320
   .X5                0.500    0.071    6.998    0.000    0.500    0.285
   .X6                0.474    0.054    8.777    0.000    0.474    0.372
   .X7                1.278    0.105   12.211    0.000    1.278    0.971
   .X8                1.023    0.084   12.204    0.000    1.023    0.967
   .X9                1.080    0.089   12.132    0.000    1.080    0.933

Trascurando le considerazioni sulla struttura fattoriale e esaminando, per esempio, unicamente il coefficiente omega, finiamo per trovare una risposta accettabile, ma sbagliata.

psych::omega(d[, 1:6])

Loading required namespace: GPArotation

Omega 
Call: omegah(m = m, nfactors = nfactors, fm = fm, key = key, flip = flip, 
    digits = digits, title = title, sl = sl, labels = labels, 
    plot = plot, n.obs = n.obs, rotate = rotate, Phi = Phi, option = option, 
    covar = covar)
Alpha:                 0.72 
G.6:                   0.76 
Omega Hierarchical:    0.55 
Omega H asymptotic:    0.65 
Omega Total            0.84 

Schmid Leiman Factor loadings greater than  0.2 
      g  F1*  F2*   F3*   h2   u2   p2
X4 0.73            0.68 1.00 0.00 0.53
X5 0.96                 0.92 0.08 1.00
X6 0.69            0.22 0.54 0.46 0.90
X7           0.56       0.33 0.67 0.03
X8           0.75       0.59 0.41 0.05
X9 0.22      0.49       0.29 0.71 0.16

With Sums of squares  of:
   g  F1*  F2*  F3* 
2.02 0.00 1.11 0.54 

general/max  1.82   max/min =   257.39
mean percent general =  0.44    with sd =  0.43 and cv of  0.97 
Explained Common Variance of the general factor =  0.55 

The degrees of freedom are 0  and the fit is  0 
The number of observations was  301  with Chi Square =  0.03  with prob <  NA
The root mean square of the residuals is  0 
The df corrected root mean square of the residuals is  NA

Compare this with the adequacy of just a general factor and no group factors
The degrees of freedom for just the general factor are 9  and the fit is  0.48 
The number of observations was  301  with Chi Square =  142.26  with prob <  3.5e-26
The root mean square of the residuals is  0.17 
The df corrected root mean square of the residuals is  0.21 

RMSEA index =  0.222  and the 10 % confidence intervals are  0.191 0.255
BIC =  90.9 

Measures of factor score adequacy             
                                                 g   F1*  F2*  F3*
Correlation of scores with factors            0.96  0.08 0.83 0.96
Multiple R square of scores with factors      0.93  0.01 0.68 0.91
Minimum correlation of factor score estimates 0.86 -0.99 0.36 0.83

 Total, General and Subset omega for each subset
                                                 g  F1*  F2*  F3*
Omega total for total scores and subscales    0.84 0.92 0.66 0.86
Omega general for total scores and subscales  0.55 0.92 0.04 0.61
Omega group for total scores and subscales    0.27 0.00 0.61 0.25

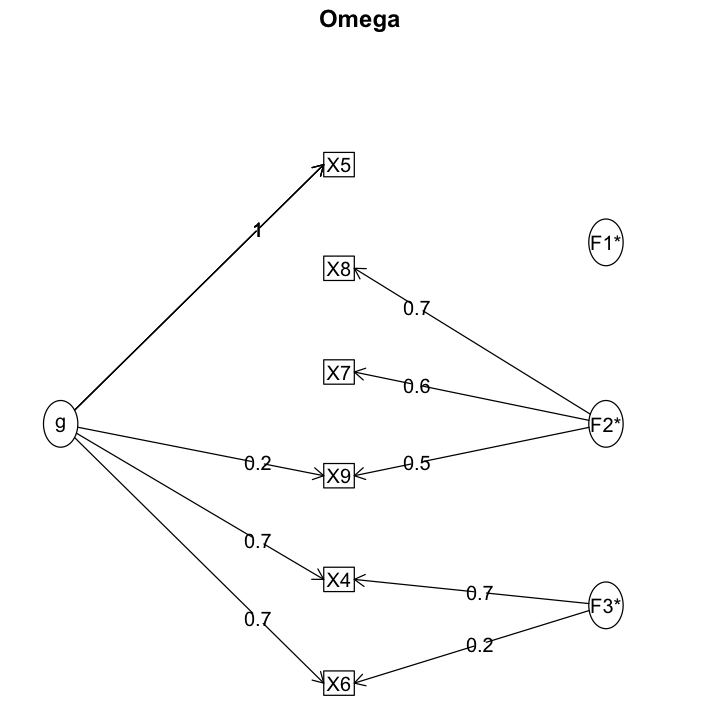
È invece necessario ipotizzare un modello congenerico a due fattori.

m2f_cong <- '
  # all loadings are uniquely estimated on each factor
  f1 =~ NA*X4 + X5 + X6
  f2 =~ NA*X7 + X8 + X9
  
  # constrain factor variancse to 1
  f1 ~~ 1*f1
  f2 ~~ 1*f2
  
  # estimate factor covariance
  f1 ~~ f2
'

# Fit above model
fit_2f_congeneric <- sem(m2f_cong, data=d)

Solo questo modello fornisce un adattamento adeguato ai dati.

out = summary(fit_2f_congeneric, fit.measures = TRUE, standardized = TRUE)
print(out)

lavaan 0.6.15 ended normally after 18 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        13

  Number of observations                           301

Model Test User Model:
                                                      
  Test statistic                                14.736
  Degrees of freedom                                 8
  P-value (Chi-square)                           0.064

Model Test Baseline Model:

  Test statistic                               568.519
  Degrees of freedom                                15
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.988
  Tucker-Lewis Index (TLI)                       0.977

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -2525.349
  Loglikelihood unrestricted model (H1)      -2517.981
                                                      
  Akaike (AIC)                                5076.698
  Bayesian (BIC)                              5124.891
  Sample-size adjusted Bayesian (SABIC)       5083.662

Root Mean Square Error of Approximation:

  RMSEA                                          0.053
  90 Percent confidence interval - lower         0.000
  90 Percent confidence interval - upper         0.095
  P-value H_0: RMSEA <= 0.050                    0.402
  P-value H_0: RMSEA >= 0.080                    0.159

Standardized Root Mean Square Residual:

  SRMR                                           0.035

Parameter Estimates:

  Standard errors                             Standard
  Information                                 Expected
  Information saturated (h1) model          Structured

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  f1 =~                                                                 
    X4                0.965    0.059   16.296    0.000    0.965    0.826
    X5                1.123    0.067   16.845    0.000    1.123    0.847
    X6                0.895    0.058   15.465    0.000    0.895    0.793
  f2 =~                                                                 
    X7                0.659    0.080    8.218    0.000    0.659    0.575
    X8                0.733    0.077    9.532    0.000    0.733    0.712
    X9                0.599    0.075    8.025    0.000    0.599    0.557

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  f1 ~~                                                                 
    f2                0.275    0.072    3.813    0.000    0.275    0.275

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    f1                1.000                               1.000    1.000
    f2                1.000                               1.000    1.000
   .X4                0.433    0.056    7.679    0.000    0.433    0.318
   .X5                0.496    0.072    6.892    0.000    0.496    0.282
   .X6                0.472    0.054    8.732    0.000    0.472    0.371
   .X7                0.881    0.100    8.807    0.000    0.881    0.670
   .X8                0.521    0.094    5.534    0.000    0.521    0.492
   .X9                0.798    0.087    9.162    0.000    0.798    0.689

13.8. Attenuazione

Un altro tema importante associato alla discussione sulla struttura fattoriale e l’attenibilità è quello dell’attenuazione. All’aumentare dell’errore di misurazione, la correlazione tra due variabili tende a diminuire. L’errore di misurazione, dunque, “maschera” l’associazione esistente tra le variabili. Tale fenomeno va sotto il nome di attenuazione.

Lord e Novick (1967) notano che, volendo determinare la relazione esistente tra due costrutti, uno psicologo può costruire opportune scale per misurarli. Se la relazione tra queste scale è lineare, allora il grado di associazione tra le scale può essere misurato dal coefficiente di correlazione. Le scale, però, contengono una componente di errore e, quindi, la correlazione empirica tra le due scale assume un valore minore della “reale” correlazione tra i costrutti. In tali circostanze, possono essere usate opportune formule per stimare il valore della correlazione disattenuata tra i tratti latenti.

Si può dimostrare che la correlazione tra i punteggi veri di due costrutti, \(T_y\) e \(T_y\), può essere espressa nei termini della correlazione \(\rho_{XY}\) tra i punteggi osservati \(X\) e \(Y\), e nei termini dei coefficienti di attenibilità \(\rho_{XX^\prime}\), \(\rho_{YY^\prime}\) dei due test:

(13.17)\[ \begin{equation} \rho(T_X, T_Y) = \frac{\rho_{XY}}{\sqrt{\rho_{XX^\prime} \rho_{YY^\prime}}} \end{equation} \]

Inoltre, può essere dimostrato che la correlazione tra i punteggi di un test e i punteggi veri di un secondo test può essere espressa nei termini delle correlazioni tra i punteggi osservati dei due test e del coefficiente di attendibilità del secondo test:

(13.18)\[ \begin{equation} \rho(X, T_Y) = \frac{\rho_{XY}}{\sqrt{\rho_{YY^\prime}}}. \end{equation} \]

13.8.1. Correlazioni disattenuate

Le (13.17) e (13.18) consentono di calcolare le cosiddette correlazioni disattenuate. L’idea è che le correlazioni tra i punteggi veri di due test sono sottostimate dalle correlazioni tra i punteggi osservati dei test, a causa dell’errore di misura. Se le attendibilità dei test sono conosciute, le (13.17) e (13.18) possono essere usate per stimare le correlazioni tra i corrispondenti punteggi veri. La teoria dell’attenuazione costituisce un’ulteriore applicazione del coefficiente di attendibilità nell’ambito della teoria classica dei test.

Le correlazioni disattenuate sono state usate già a partire dal 1904 da Spearman. Nell’esempio di Spearman, \(X\) era una misura di discriminazione dell’altezza di un suono (pitch discrimination) e \(Y\) era una misura di intelligenza fornita da un insegnante. La correlazione tra queste due misure era \(\hat{\rho}_{XY}=0.38\). Le attendibilità delle due misure erano pari a, rispettivamente, \(\hat{\rho}_{XX'}= 0.25\) e \(\hat{\rho}_{YY'}= 0.55\). In base alla (13.18)

\[ \rho(X, T_Y) = \frac{\rho_{XY}}{\sqrt{\rho_{YY^\prime}}} \]

la correlazione predetta tra i valori veri di pitch discrimination e i valori empirici dell’intelligenza è

\[ \hat{\rho}(X, T_Y) =\frac{0.38}{\sqrt{0.25}}=0.76. \]

In base alla (13.17)

\[ \rho(T_X, T_Y) = \frac{\rho_{XY}}{\sqrt{\rho_{XX'} \rho_{YY'}}} \]

la correlazione tra i valori veri di pitch discrimination e i valori veri dell’intelligenza è

\[ \hat{\rho}(T_X, T_Y) =\frac{0.38}{\sqrt{0.25 \times 0.55}}=1.025. \]

Si noti come i limiti di questa procedura emergano già dall’esempio fornito da Spearman: le correlazioni disattenuate possono facilmente produrre una sovrastima.

Questa formula originò una controversia tra Charles Spearman e Karl Pearson. In un suo articolo del 1904 (lo stesso anno dei famosi articoli di Spearman), Pearson riportò diverse correlazioni nell’intorno di 0.5 che riguardavano la misurazione empirica di caratteristiche quali la vivacità e l’introspezione. Spearman criticò l’articolo di Pearson affermando che le osservazioni probabilmente contenevano un sostanziale errore di misurazione, il che determinava il fatto che fossero così basse. Le corrispondenti correlazioni disattenuate erano, secondo Spearman, probabilmente molto più alte. Tale critica venne del tutto ignorata da Pearson sulla base del fatto che la formula di Spearman poteva condurre a correlazioni maggiori di uno. Inoltre, Pearson non accettava i riferimenti a quantità inosservabili. Spearman, d’altra parte, eseguì diversi studi su variabili psicologiche alle quali applicò la sua formula per le correlazioni disattenuate. In molti casi, trovò che le correlazioni disattenuate erano vicine ad uno. Questo suggeriva che tali variabili psicologiche erano indicatori dello stesso fenomeno. Queste considerazioni spinsero Spearman a procedere in questa direzione, giungendo ad inventare l’analisi fattoriale così com’è riportata nell’articolo del 1904 “General intelligence”, objectively determined and measured.

McDonald (1999) afferma che le correlazioni disattenuate devono essere usate con cautela. Un metodo migliore per calcolare le correlazioni tra le variabili latenti (ovvero, le correlazioni non “inquinate” dagli errori di misura) è quello di costruire un modello di equazioni strutturali nel quale diverse ipotesi possono essere direttamente verificate, compresa quella della correlazione tra le variabili latenti.

13.9. Attendibilità e scala di misura

McDonald (2013) fa notare che i coefficienti \(\omega\) e \(\alpha\), ma non il coefficiente di Spearman-Brown, dipendono dalla scala di misura degli item. Stimare \(\omega\) utilizzando una matrice di correlazione anziché una matrice di varianze e di covarianze è equivalente a stimare il coefficiente di attendibilità di una somma di item standardizzati. Il risultato ottenuto mediante \(\omega\) e \(\alpha\) non si generalizza però al caso in cui si voglia valutare l’attendibilità del punteggio totale di un test calcolato sui valori grezzi degli item.

Il modello ad un fattore comune non dipende dall’unità di misura degli indicatori e può essere adattato sia ad una matrice di correlazione sia ad una matrice di varianze e di covarianze. Il calcolo dei coefficienti \(\omega\) e \(\alpha\), invece, deve essere fatto sulla soluzione trovata utilizzando una matrice di varianze e di covarianze.

13.10. Quale indice usare?

L’indice di attendibilità più diffuso in letteratura è il coefficiente \(\alpha\) di Cronbach. Affinché \(\alpha\) fornisca una stima dell’attendibilità del test, però, gli item devono essere \(\tau\)-equivalenti. Il modello di \(\tau\)-equivalenza richiede l’unidimensionalità del tratto latente. In pratica, tale assunzione viene spesso violata, dato che la maggior parte dei test, oltre ad un fattore generale, misurano anche altri fattori. Anche nel caso di un test unidimensionale, le comunalità degli item non sono mai uguali tra loro, violando così l’assunzione di \(\tau\)-equivalenza. In tali circostanze, se risulta soddisfatta l’assunzione di incorrelazione degli errori, il coefficiente \(\alpha\) sottostima l’attendibilità del test. Se invece l’assunzione di incorrelazione degli errori non risulta soddisfatta, allora il coefficiente \(\alpha\) sovrastima l’attendibilità del test. Per tali ragioni, l’utilità del coefficiente \(\alpha\) di Cronbach è molto limitata e, in generale, è preferibile usare il coefficiente \(\omega\) (McDonald, 1999). Altre alternative sono gli indici \(glb\) (Greatest Lower Bound; si veda, ad esempio, Ten Berge e Sočan, 2004) e \(\beta\) (Revelle, 1979).