10. Il modello multifattoriale

10.1. Modello multifattoriale: fattori ortogonali

La teoria dei due fattori ha orientato per diversi anni le ricerche sull’intelligenza, finché Thurstone (1945) non propose una sua modifica, conosciuta come teoria multifattoriale. Secondo Thurstone la covariazione tra le variabili manifeste non può essere spiegata da un unico fattore generale. Invece è necessario ipotizzare l’azione causale di diversi fattori, definiti comuni, i quali si riferiscono solo ad alcune delle variabili considerate.

Il modello plurifattoriale assume che ciascuna variabile manifesta sia espressa come funzione lineare di un certo numero \(m\) di fattori comuni, \(\xi_1, \xi_2, \dots, \xi_m\), responsabili della correlazione con le altre variabili, e di un solo fattore specifico (termine d’errore), responsabile della variabilità della variabile stessa. Per \(p\) variabili manifeste, \(Y_1, Y_2, \dots, Y_p\), il modello fattoriale diventa quello indicato dal sistema di equazioni lineari descritto di seguito. Idealmente, \(m\) dovrebbe essere molto più piccolo di \(p\) così da consentire una descrizione parsimoniosa delle variabili manifeste in funzione di pochi fattori soggiacenti.

Le variabili manifeste \(Y\) sono indicizzate da \(i = 1, \dots, p.\) Le variabili latenti \(\xi\) (fattori) sono indicizzate da \(j = 1, \dots, m.\) I fattori specifici \(\delta\) sono indicizzati da \(i = 1, \dots, p.\) Le saturazioni fattoriali si distinguono dunque tramite due indici, \(i\) e \(j\): il primo indice si riferisce alle variabili manifeste, il secondo si riferisce ai fattori latenti.

Indichiamo con \(\mu_i\), con \(i=1, \dots, p\) le medie delle \(p\) variabili manifeste \(Y_1, Y_2, \dots, Y_p\). Se non vi è alcun effetto delle variabili comuni latenti, allora la variabile \(Y_{ijk}\), dove \(k\) è l’indice usato per i soggetti, sarà uguale a:

\[\begin{split} \begin{equation} \begin{cases} Y_{1k} &= \mu_1 + \delta_{1k} \\ &\vdots\\ Y_{ik} &= \mu_i + \delta_{ik}\\ &\vdots\\ Y_{pk} &= \mu_p + \delta_{pk} \notag \end{cases} \end{equation} \end{split}\]

Se invece le variabili manifeste rappresentano la somma dell’effetto causale di \(m\) fattori comuni e di \(p\) fattori specifici, allora possiamo scrivere:

\[\begin{split} \begin{equation} \begin{cases} Y_1 - \mu_1 &= \lambda_{11}\xi_1 + \dots + \lambda_{1k}\xi_k \dots +\lambda_{1m}\xi_m + \delta_1 \\ &\vdots\\ Y_i - \mu_i &= \lambda_{i1}\xi_1 + \dots + \lambda_{ik}\xi_k \dots +\lambda_{im}\xi_m + \delta_i\\ &\vdots\\ Y_p - \mu_p &= \lambda_{p1}\xi_1 + \dots + \lambda_{pk}\xi_k \dots +\lambda_{pm}\xi_m + \delta_p \notag \end{cases} \end{equation} \end{split}\]

Nel precedente sistema di equazioni lineari,

• \(\xi_j\), con \(j=1, \dots, m\), rappresenta la \(j\)-esima variabile inosservabile a fattore comune (ossia il \(j\)-esimo fattore comune a tutte le variabili \(Y_i\));

• \(\lambda_{ij}\) rappresenta il parametro, detto saturazione o peso fattoriale, che riflette l’importanza del \(j\)-esimo fattore comune nella composizione della \(i\)-esima variabile osservabile;

• \(\delta_i\) rappresenta il fattore specifico (o unico) di ogni variabile manifesta \(Y_i\).

In conclusione, secondo il modello multifattoriale, le variabili manifeste \(Y_i\), con \(i=1, \dots, p\), sono il risultato di una combinazione lineare di \(m < p\) fattori inosservabili ad esse comuni \(\xi_j\), con \(j=1, \dots, m\), e di \(p\) fattori specifici \(\delta_i\), con \(i=1, \dots, p\), anch’essi inosservabili e di natura residua.

10.1.1. Assunzioni del modello multifattoriale

Le variabili inosservabili a fattore comune \(\xi_j\), con \(j=1, \dots, m\), in quanto latenti, non possiedono unità di misura. Pertanto, per semplicità si assume che abbiano media zero, \(\mathbb{E}(\xi_j)=0\), abbiano varianza unitaria, \(\mathbb{V} (\xi_j)= \mathbb{E}(\xi_j^2) - [\mathbb{E}(\xi_j)]^2=1\), e siano incorrelate tra loro, \(Cov(\xi_j, \xi_h)=0\), con \(j, h = 1, \dots, m; \;j \neq h\). Si assume inoltre che le variabili a fattore specifico \(\delta_i\) siano tra loro incorrelate, \(Cov(\delta_i,\delta_k)=0\), con \(i, k = 1, \dots, p, \; i \neq k\), abbiano media zero, \(\mathbb{E}(\delta_i)=0\), e varianza uguale a \(\mathbb{V} (\delta_i) = \psi_{ii}\). La varianza \(\psi_{ii}\) è detta varianza specifica o unicità della \(i\)-esima variabile manifesta \(Y_i\). Si assume infine che i fattori specifici siano linearmente incorrelati con i fattori comuni, ovvero \(Cov(\xi_j, \delta_i)=0\) per ogni \(j=1, \dots, m\) e per ogni \(i=1\dots,p\).

10.1.2. Interpretazione dei parametri del modello

10.1.2.1. Covarianza tra variabili e fattori

Nell’ipotesi che le variabili \(Y_i\) abbiano media nulla, la covarianza tra \(Y_i\) e \(\xi_j\) è uguale alla saturazione fattoriale \(\lambda_{ij}\):

\[\begin{split} \begin{equation} \begin{aligned} Cov(Y_i, \xi_j) &= \mathbb{E}(Y_i \xi_j)\notag\\ &=\mathbb{E}\left[(\lambda_{i1} \xi_1 + \dots + \lambda_{im} \xi_m + \delta_i)\xi_j \right]\notag\\ &= \lambda_{i1}\underbrace{\mathbb{E}(\xi_1\xi_j)}_{=0} + \dots + \lambda_{ij}\underbrace{\mathbb{E}(\xi_j^2)}_{=1} + \dots \notag\\ & \; + \lambda_{im}\underbrace{\mathbb{E}(\xi_m\xi_j)}_{=0} + \underbrace{\mathbb{E}(\delta_i \xi_j)}_{=0}\notag\\ &= \lambda_{ij}.\notag \end{aligned} \end{equation} \end{split}\]

Anche nel modello multifattoriale, dunque, le saturazioni fattoriali rappresentano le covarianze tra le variabili e i fattori:

\[ Cov(Y_i, \xi_j) = \lambda_{ij} \qquad i=1, \dots, p; \quad j= 1, \dots, m. \]

Naturalmente, se le variabili sono standardizzate, le saturazioni fattoriali diventano correlazioni:

\[ r_{ij} = \lambda_{ij}. \]

10.1.2.2. Espressione fattoriale della varianza

Come nel modello monofattoriale, la varianza delle variabili manifeste si decompone in una componente dovuta ai fattori comuni, chiamata comunalità, e in una componente specifica alle \(Y_i\), chiamata unicità. Nell’ipotesi che le variabili \(Y_i\) abbiano media nulla, la varianza di \(Y_i\) è uguale a

(10.1)\[ \begin{equation} \begin{aligned} \mathbb{V} (Y_i) &=\mathbb{E}\left[ (\lambda_{i1} \xi_1 + \dots + \lambda_{im} \xi_m + \delta_i)^2 \right]. \end{aligned} \end{equation} \]

Come si sviluppa il polinomio precedente? Il quadrato di un polinomio è uguale alla somma dei quadrati di tutti i termini più il doppio prodotto di ogni termine per ciascuno di quelli che lo seguono. Il valore atteso del quadrato del primo termine è uguale a \(\lambda_{i1}^2\mathbb{E}(\xi_1^2)\) ma, essendo la varianza di \(\xi_1\) uguale a \(1\), otteniamo semplicemente \(\lambda_{i1}^2\). Lo stesso vale per i quadrati di tutti i termini seguenti tranne l’ultimo. Infatti, \(\mathbb{E}(\delta_i^2)=\psi_{ii}\). Per quel che riguarda i doppi prodotti, sono tutti nulli. In primo luogo perché, nel caso di fattori ortogonali, la covarianza tra i fattori comuni è nulla, \(\mathbb{E}(\xi_j \xi_h)=0\), con \(j \neq h\). In secondo luogo perché il fattori comuni cono incorrelati con i fattori specifici, quindi \(\mathbb{E}(\delta_i \xi_j)=0\).

In conclusione,

\[\begin{split} \begin{equation} \begin{aligned} \mathbb{V}(Y_i) &= \lambda_{i1}^2 + \lambda_{i2}^2 + \dots + \lambda_{im}^2 + \psi_{ii} \notag\\ &= \sum_{j=1}^m \lambda_{ij}^2 + \psi_{ii}\notag\\ &= h_i^2 + \psi_{ii}\notag\\ &=\text{communalità} + \text{unicità},\notag \end{aligned} \end{equation} \end{split}\]

la varianza della variabile manifesta \(Y_i\) è suddivisa in due parti: il primo addendo è definito comunalità poiché rappresenta la parte di variabilità della \(Y_i\) spiegata dai fattori comuni; il secondo addendo è invece definito varianza specifica (o unicità) poiché esprime la parte di variabilità della \(Y_i\) non spiegata dai fattori comuni.

10.1.2.3. Espressione fattoriale della covarianza

Quale esempio, consideriamo il caso di \(p=5\) variabili osservabili e \(m=2\) fattori ortogonali. Se le variabili manifeste sono ‘centrate’ (ovvero, se a ciascuna di esse sottraiamo la rispettiva media), allora il modello multifattoriale diventa

\[\begin{split} \begin{equation} \begin{aligned} Y_1 &= \lambda_{11} \xi_1 + \lambda_{12} \xi_2 + \delta_1,\notag\\ Y_2 &= \lambda_{21} \xi_1 + \lambda_{22} \xi_2 + \delta_2,\notag\\ Y_3 &= \lambda_{31} \xi_1 + \lambda_{32} \xi_2 + \delta_3,\notag\\ Y_4 &= \lambda_{41} \xi_1 + \lambda_{42} \xi_2 + \delta_4,\notag\\ Y_5 &= \lambda_{51} \xi_1 + \lambda_{52} \xi_2 + \delta_5.\notag \end{aligned} \end{equation} \end{split}\]

Nell’ipotesi che le variabili \(Y_i\) abbiano media nulla, la covarianza tra \(Y_1\) e \(Y_2\), ad esempio, è uguale a:

\[\begin{split} \begin{equation} \begin{aligned} Cov(Y_1, Y_2) &= \mathbb{E}\left( Y_1 Y_2\right) \notag\\ &= \mathbb{E}\left[ (\lambda_{11} \xi_1 + \lambda_{12} \xi_2 + \delta_1) (\lambda_{21} \xi_1 + \lambda_{22} \xi_2 + \delta_2) \right]\notag\\ &= \lambda_{11} \lambda_{21} \mathbb{E}(\xi_1^2) + \lambda_{11} \lambda_{22} \mathbb{E}(\xi_1 \xi_2) +\notag \lambda_{11} \mathbb{E}(\xi_1 \delta_2) +\notag\\ &\quad \lambda_{12} \lambda_{21}\mathbb{E}(\xi_1 \xi_2)\, + \lambda_{12} \lambda_{22}\mathbb{E}(\xi^2_2)\, + \lambda_{12} \mathbb{E}(\xi_2\delta_2) +\notag\\ &\quad \lambda_{21} \mathbb{E}(\xi_1\delta_1) +\notag \lambda_{22} \mathbb{E}(\xi_2\delta_1) + \mathbb{E}(\delta_1 \delta_2)\notag\\ &= \lambda_{11} \lambda_{21} + \lambda_{12} \lambda_{22}.\notag \end{aligned} \end{equation}\end{split}\]

In conclusione, la covarianza tra le variabili manifeste \(Y_l\) e \(Y_m\) riprodotta dal modello è data dalla somma dei prodotti delle saturazioni \(\lambda_l \lambda_m\) nei due fattori.

Esempio. Consideriamo i dati riportati da Brown [Bro15], ovvero otto misure di personalità raccolte su un campione di 250 pazienti che hanno concluso un programma di psicoterapia. Le scale sono le seguenti:

• anxiety (N1),

• hostility (N2),

• depression (N3),

• self-consciousness (N4),

• warmth (E1),

• gregariousness (E2),

• assertiveness (E3),

• positive emotions (E4).

varnames <- c("N1", "N2", "N3", "N4", "E1", "E2", "E3", "E4")
sds <- '5.7  5.6  6.4  5.7  6.0  6.2  5.7  5.6'

cors <- '
 1.000
 0.767  1.000 
 0.731  0.709  1.000 
 0.778  0.738  0.762  1.000 
-0.351  -0.302  -0.356  -0.318  1.000 
-0.316  -0.280  -0.300  -0.267  0.675  1.000 
-0.296  -0.289  -0.297  -0.296  0.634  0.651  1.000 
-0.282  -0.254  -0.292  -0.245  0.534  0.593  0.566  1.000'

psychot_cor_mat <- getCov(cors, names = varnames)
n <- 250

Eseguiamo l’analisi fattoriale esplorativa con il metodo della massima verosimiglianza ipotizzando due fattori comuni incorrelati:

n_facs <- 2
fit_efa <- factanal(
  covmat = psychot_cor_mat,
  factors = n_facs,
  rotation = "varimax",
  n.obs = n
)

Esaminiamo le saturazioni fattoriali:

lambda <- fit_efa$loadings
print(lambda)

Loadings:
   Factor1 Factor2
N1  0.854  -0.228 
N2  0.826  -0.194 
N3  0.811  -0.233 
N4  0.865  -0.186 
E1 -0.202   0.773 
E2 -0.139   0.829 
E3 -0.158   0.771 
E4 -0.147   0.684 

               Factor1 Factor2
SS loadings      2.923   2.526
Proportion Var   0.365   0.316
Cumulative Var   0.365   0.681

La soluzione fattoriale conferma la presenza di due fattori: il primo fattore satura sulle scale di neutoricismo, il secono sulle scale di estroversione.

La correlazione riprodotta \(r_{12}\) è uguale a \(\lambda_{11}\lambda_{21} + \lambda_{12}\lambda_{22}\)

lambda[1, 1] * lambda[2, 1] + lambda[1, 2] * lambda[2, 2]

0.74928439937518

e corrisponde da vicino alla correlazione osservata 0.767.

L’intera matrice di correlazioni riprodotte è \(\boldsymbol{\Lambda} \boldsymbol{\Lambda}^{\mathsf{T}} + \boldsymbol{\psi}\):

Rr <- lambda %*% t(lambda) + diag(fit_efa$uniq)
Rr %>% 
  round(3)

A matrix: 8 × 8 of type dbl

	N1	N2	N3	N4	E1	E2	E3	E4
N1	1.000	0.749	0.745	0.781	-0.348	-0.307	-0.311	-0.281
N2	0.749	1.000	0.715	0.751	-0.317	-0.276	-0.281	-0.254
N3	0.745	0.715	1.000	0.745	-0.344	-0.306	-0.308	-0.279
N4	0.781	0.751	0.745	1.000	-0.318	-0.274	-0.280	-0.254
E1	-0.348	-0.317	-0.344	-0.318	1.000	0.669	0.628	0.558
E2	-0.307	-0.276	-0.306	-0.274	0.669	1.000	0.661	0.587
E3	-0.311	-0.281	-0.308	-0.280	0.628	0.661	1.000	0.550
E4	-0.281	-0.254	-0.279	-0.254	0.558	0.587	0.550	1.000

La differenza tra la matrice di correlazioni riprodotte e la matrice di correlazioni osservate è uguale a:

(psychot_cor_mat - Rr) %>% 
  round(3)

A matrix: 8 × 8 of type dbl

	N1	N2	N3	N4	E1	E2	E3	E4
N1	0.000	0.018	-0.014	-0.003	-0.003	-0.009	0.015	-0.001
N2	0.018	0.000	-0.006	-0.013	0.015	-0.004	-0.008	0.000
N3	-0.014	-0.006	0.000	0.017	-0.012	0.006	0.011	-0.013
N4	-0.003	-0.013	0.017	0.000	0.000	0.007	-0.016	0.009
E1	-0.003	0.015	-0.012	0.000	0.000	0.006	0.006	-0.024
E2	-0.009	-0.004	0.006	0.007	0.006	0.000	-0.010	0.006
E3	0.015	-0.008	0.011	-0.016	0.006	-0.010	0.000	0.016
E4	-0.001	0.000	-0.013	0.009	-0.024	0.006	0.016	0.000

Esempio. Consideriamo nuovamente i dati precedenti ma, in questo caso, eseguiamo un’analisi fattoriale confermativa. Usando lavaan il modello diventa:

cfa_mod <- "
  N =~ N1 + N2 + N3 + N4
  E =~ E1 + E2 + E3 + E4
"

fit_cfa <- lavaan::cfa(
  cfa_mod,
  sample.cov = psychot_cor_mat,
  sample.nobs = n,
  orthogonal = TRUE,
  std.lv = TRUE
)

Il path diagram si ottiene nel modo seguente:

semPaths(
  fit_cfa,
  "std", 
  posCol = c("black"),
  edge.label.cex = 1.2, 
  sizeMan = 7
  )

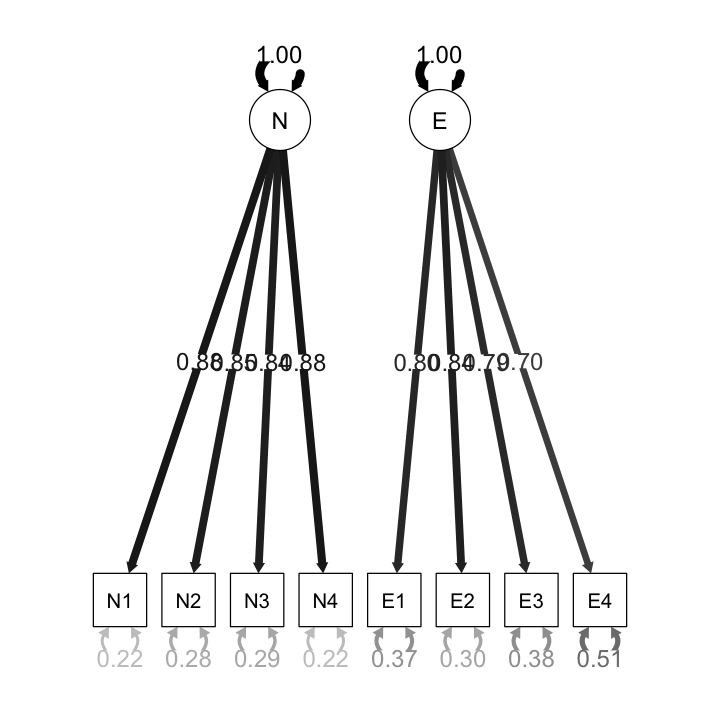
Esaminiamo le saturazioni fattoriali:

parameterEstimates(fit_cfa, standardized = TRUE) %>%
  dplyr::filter(op == "=~") %>%
  dplyr::select(
    "Latent Factor" = lhs, 
    Indicator = rhs, 
    B = est, 
    SE = se, 
    Z = z, 
    "p-value" = pvalue, 
    Beta = std.all) %>%
  knitr::kable(digits = 3, booktabs = TRUE, format = "markdown", 
               caption = "Factor Loadings")

Table: Factor Loadings

|Latent Factor |Indicator |     B|    SE|      Z| p-value|  Beta|
|:-------------|:---------|-----:|-----:|------:|-------:|-----:|
|N             |N1        | 0.882| 0.051| 17.422|       0| 0.884|
|N             |N2        | 0.847| 0.052| 16.340|       0| 0.849|
|N             |N3        | 0.840| 0.052| 16.134|       0| 0.842|
|N             |N4        | 0.882| 0.051| 17.432|       0| 0.884|
|E             |E1        | 0.795| 0.056| 14.276|       0| 0.796|
|E             |E2        | 0.838| 0.054| 15.369|       0| 0.839|
|E             |E3        | 0.788| 0.056| 14.097|       0| 0.789|
|E             |E4        | 0.697| 0.058| 11.942|       0| 0.699|

Il risultato sembra sensato: le saturazioni su ciascun fattore sono molto alte. Tuttavia, la matrice delle correlazioni residue

cor_table <- residuals(fit_cfa, type = "cor")$cov
knitr::kable(
  cor_table, 
  digits = 3, 
  format = "markdown", 
  booktabs = TRUE
)

|   |     N1|     N2|     N3|     N4|     E1|     E2|     E3|     E4|
|:--|------:|------:|------:|------:|------:|------:|------:|------:|
|N1 |  0.000|  0.017| -0.013| -0.003| -0.351| -0.316| -0.296| -0.282|
|N2 |  0.017|  0.000| -0.006| -0.012| -0.302| -0.280| -0.289| -0.254|
|N3 | -0.013| -0.006|  0.000|  0.018| -0.356| -0.300| -0.297| -0.292|
|N4 | -0.003| -0.012|  0.018|  0.000| -0.318| -0.267| -0.296| -0.245|
|E1 | -0.351| -0.302| -0.356| -0.318|  0.000|  0.007|  0.006| -0.022|
|E2 | -0.316| -0.280| -0.300| -0.267|  0.007|  0.000| -0.011|  0.007|
|E3 | -0.296| -0.289| -0.297| -0.296|  0.006| -0.011|  0.000|  0.015|
|E4 | -0.282| -0.254| -0.292| -0.245| -0.022|  0.007|  0.015|  0.000|

rivela che il modello ipotizzato dall’analisi fattoriale confermativa non è adeguato.

10.2. Modello fattoriale: Fattori obliqui

Anche nel caso di fattori comuni correlati è possibile esprimere nei termini dei parametri del modello la covarianza teorica tra una variabile manifesta \(Y_i\) e uno dei fattori comuni, la covarianza teorica tra due variabili manifeste, e la comunalità di ciascuna variabile manifesta. Dato però che i fattori comuni risultano correlati, l’espressione fattoriale di tali quantità è più complessa che nel caso di fattori comuni ortogonali.

10.2.1. Covarianza teorica tra variabili e fattori

In base al modello multifattoriale con \(m\) fattori comuni la variabile \(Y_i\) è

\[ Y_i = \lambda_{i1} \xi_1 + \dots + \lambda_{im} \xi_m + \delta_i. (\#eq:mod-multifact) \]

Poniamoci il problema di trovare la covarianza teorica tra la variabile manifesta \(Y_i\) e il fattore comune \(\xi_j\). Come in precedenza, il problema si riduce a quello di trovare \(\mathbb{E}(Y_i \xi_j)\). Ne segue che

\[\begin{split} \begin{equation} \begin{aligned} Cov(Y_i, \xi_j) &= \mathbb{E}(Y_i \xi_j)\notag\\ &=\mathbb{E}\left[(\lambda_{i1} \xi_1 + \dots + \lambda_{ij} \xi_j + \dots + \lambda_{im} \xi_m + \delta_i)\xi_j \right]\notag\\ &= \lambda_{i1}\underbrace{\mathbb{E}(\xi_1\xi_j)}_{\neq 0} + \dots + \lambda_{ij}\underbrace{\mathbb{E}(\xi_j^2)}_{=1} + \dots \notag\\ & \quad + \lambda_{im}\underbrace{\mathbb{E}(\xi_m\xi_j)}_{\neq 0} + \underbrace{\mathbb{E}(\delta_i \xi_j)}_{=0}\notag\\ &= \lambda_{ij} + \lambda_{i1} Cov(\xi_1, \xi_j) + \dots + \lambda_{im} Cov(\xi_m, \xi_j). \end{aligned} \end{equation} \end{split}\]

Ad esempio, nel caso di tre fattori comuni \(\xi_1, \xi_2, \xi_3\), la covarianza tra \(Y_1\) e \(\xi_{1}\) diventa

\[ \lambda_{11} + \lambda_{12}Cov(\xi_1, \xi_2) + \lambda_{13}Cov(\xi_1, \xi_3). \]

10.2.2. Espressione fattoriale della varianza

Poniamoci ora il problema di trovare la varianza teorica della variabile manifesta \(Y_i\). In base al modello fattoriale, la variabile \(Y_i\) è specificata come nella @ref(eq:mod-multifact). La varianza di \(Y_i\) è \(\mathbb{V}(Y_i) = \mathbb{E}(Y_i^2) -[\mathbb{E}(Y_i)]^2\). Però, avendo espresso \(Y_i\) nei termini della differenza dalla sua media, l’espressione della varianza si riduce a \(\mathbb{V}(Y_i) = \mathbb{E}(Y_i^2)\). Dobbiamo dunque sviluppare l’espressione

\[ \mathbb{E}(Y_i^2) = \mathbb{E}[(\lambda_{i1} \xi_1 + \dots + \lambda_{im} \xi_m + \delta_i)^2]. \]

In conclusione, la varianza teorica di \(Y_i\) è uguale a

\[\begin{split} \begin{equation} \begin{split} \mathbb{V}(Y_i) &= \lambda_{i1}^2 + \lambda_{i2}^2 + \dots + \lambda_{im}^2 + \\ &\quad 2 \lambda_{i1} \lambda_{i2} Cov(\xi_1, \xi_2) + \dots + 2 \lambda_{i,m-1} \lambda_{im} Cov(\xi_{m-1}, \xi_m) + \\ &\quad \psi_{ii}.\notag \end{split} \end{equation} \end{split}\]

Ad esempio, nel caso di tre fattori comuni, \(\xi_1, \xi_2, \xi_3\), la varianza di \(Y_1\) è

\[\begin{split} \begin{equation} \begin{split} \mathbb{V}(Y_1) = &\lambda_{11}^2 + \lambda_{12}^2 + \lambda_{13}^2 +\\ &\quad 2 \lambda_{11} \lambda_{12} Cov(\xi_1, \xi_2) + \\ &\quad 2 \lambda_{11} \lambda_{13} Cov(\xi_1, \xi_3) + \\ &\quad 2 \lambda_{12} \lambda_{13} Cov(\xi_2, \xi_3) + \\ &\quad \psi_{11}. \notag \end{split} \end{equation} \end{split}\]

10.2.3. Covarianza teorica tra due variabili

Consideriamo ora il caso più semplice di due soli fattori comuni correlati e calcoliamo la covarianza tra \(Y_1\) e \(Y_2\):

\[\begin{split} \begin{equation} \begin{aligned} \mathbb{E}(Y_1 Y_2) =\mathbb{E}[(&\lambda_{11}\xi_1 + \lambda_{12}\xi_2+\delta_1) (\lambda_{21}\xi_1 + \lambda_{22}\xi_2+\delta_2)]\notag\\ =\mathbb{E}( &\lambda_{11}\lambda_{21}\xi_1^2 + \lambda_{11}\lambda_{22}\xi_1\xi_2 + \lambda_{11}\xi_1\delta_2 +\notag\\ +&\lambda_{12}\lambda_{21}\xi_1\xi_2 + \lambda_{12}\lambda_{22}\xi_2^2 + \lambda_{12}\xi_2\delta_2 +\notag\\ +&\lambda_{21}\xi_1\delta_1 + \lambda_{22}\xi_2\delta_1 + \delta_1\delta_2).\notag \end{aligned} \end{equation} \end{split}\]

Distribuendo l’operatore di valore atteso, dato che \(\mathbb{E}(\xi^2)=1\) e \(\mathbb{E}(\xi \delta)=0\), otteniamo

\[ Cov(Y_1, Y_2) = \lambda_{11} \lambda_{21} + \lambda_{12} \lambda_{22} + \lambda_{12} \lambda_{21}Cov(\xi_1, \xi_2) +\lambda_{11} \lambda_{22}Cov(\xi_1, \xi_2). \]

In termini matriciali si scrive

\[ \boldsymbol{\Sigma} =\boldsymbol{\Lambda} \boldsymbol{\Phi} \boldsymbol{\Lambda}^{\mathsf{T}} + \boldsymbol{\Psi}, \]

dove \(\boldsymbol{\Phi}\) è la matrice di ordine \(m \times m\) di varianze e covarianze tra i fattori comuni e \(\boldsymbol{\Psi}\) è una matrice diagonale di ordine \(p\) con le unicità delle variabili.

Esempio. Consideriamo nuovamente i dati esaminati negli esercizi precedenti, ma questa volta il modello consente una correlazione tra i due fattori comuni:

fit2_cfa <- lavaan::cfa(
  cfa_mod,
  sample.cov = psychot_cor_mat,
  sample.nobs = n,
  orthogonal = FALSE,
  std.lv = TRUE
)

Visualizziamo il modello nel modo seguente:

semPaths(
  fit2_cfa,
  "std", 
  posCol = c("black"),
  edge.label.cex = 1.1, 
  sizeMan = 7
  )

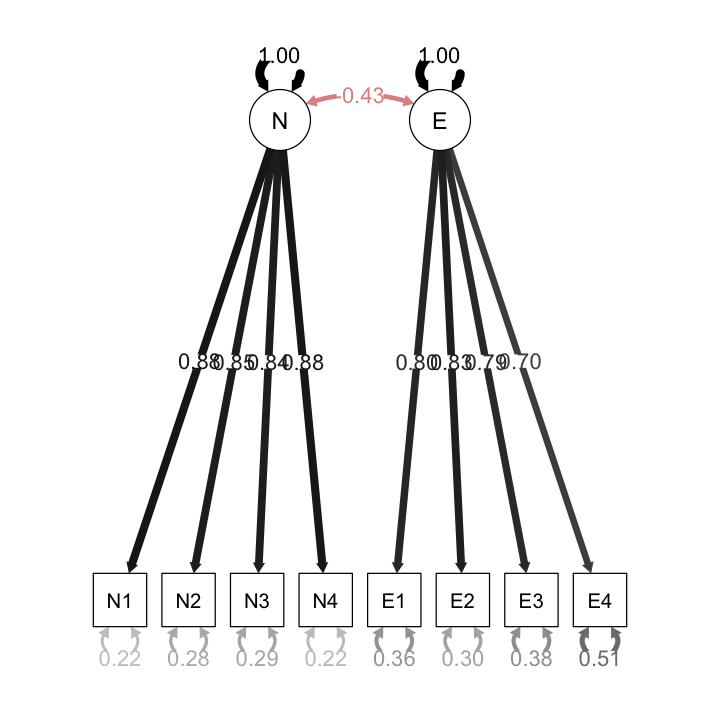
Esaminiamo le saturazioni fattoriali:

parameterEstimates(fit2_cfa, standardized = TRUE) %>%
  dplyr::filter(op == "=~") %>%
  dplyr::select(
    "Latent Factor" = lhs, 
    Indicator = rhs, 
    B = est, 
    SE = se, 
    Z = z, 
    "p-value" = pvalue, 
    Beta = std.all) %>%
  knitr::kable(digits = 3, booktabs = TRUE, format = "markdown", 
               caption = "Factor Loadings")

Table: Factor Loadings

|Latent Factor |Indicator |     B|    SE|      Z| p-value|  Beta|
|:-------------|:---------|-----:|-----:|------:|-------:|-----:|
|N             |N1        | 0.883| 0.051| 17.472|       0| 0.885|
|N             |N2        | 0.847| 0.052| 16.337|       0| 0.849|
|N             |N3        | 0.842| 0.052| 16.190|       0| 0.844|
|N             |N4        | 0.880| 0.051| 17.381|       0| 0.882|
|E             |E1        | 0.800| 0.055| 14.465|       0| 0.802|
|E             |E2        | 0.832| 0.054| 15.294|       0| 0.834|
|E             |E3        | 0.788| 0.056| 14.150|       0| 0.789|
|E             |E4        | 0.698| 0.058| 11.974|       0| 0.699|

Le saturazioni sono simili a quelle che abbiamo trovato in precedenza, In questo caso, però, la matrice delle correlazioni residue è adeguata:

cor_table <- residuals(fit2_cfa, type = "cor")$cov
knitr::kable(
  cor_table, 
  digits = 3, 
  format = "markdown", 
  booktabs = TRUE
)

|   |     N1|     N2|     N3|     N4|     E1|     E2|     E3|     E4|
|:--|------:|------:|------:|------:|------:|------:|------:|------:|
|N1 |  0.000|  0.016| -0.015| -0.002| -0.042|  0.005|  0.008| -0.013|
|N2 |  0.016|  0.000| -0.007| -0.010| -0.006|  0.028|  0.002|  0.004|
|N3 | -0.015| -0.007|  0.000|  0.018| -0.062|  0.006| -0.007| -0.035|
|N4 | -0.002| -0.010|  0.018|  0.000| -0.010|  0.053|  0.007|  0.023|
|E1 | -0.042| -0.006| -0.062| -0.010|  0.000|  0.006|  0.001| -0.027|
|E2 |  0.005|  0.028|  0.006|  0.053|  0.006|  0.000| -0.007|  0.010|
|E3 |  0.008|  0.002| -0.007|  0.007|  0.001| -0.007|  0.000|  0.014|
|E4 | -0.013|  0.004| -0.035|  0.023| -0.027|  0.010|  0.014|  0.000|

Esempio. Esaminiamo più da vicino la matrice di correlazioni riprodotta dal modello, nel caso di fattori obliqui. Le saturazioni fattoriali sono:

lambda <- inspect(fit2_cfa, what="std")$lambda
lambda

A lavaan.matrix: 8 × 2 of type dbl

	N	E
N1	0.8848214	0.0000000
N2	0.8485128	0.0000000
N3	0.8436432	0.0000000
N4	0.8819736	0.0000000
E1	0.0000000	0.8018485
E2	0.0000000	0.8337599
E3	0.0000000	0.7894530
E4	0.0000000	0.6990366

La matrice di intercorrelazoni fattoriali è

Phi <- inspect(fit2_cfa, what="std")$psi
Phi

A lavaan.matrix.symmetric: 2 × 2 of type dbl

	N	E
N	1.000000	-0.434962
E	-0.434962	1.000000

Le varianze residue sono:

Psi <- inspect(fit2_cfa, what="std")$theta
Psi

A lavaan.matrix.symmetric: 8 × 8 of type dbl

	N1	N2	N3	N4	E1	E2	E3	E4
N1	0.217091	0.0000000	0.0000000	0.0000000	0.000000	0.0000000	0.000000	0.0000000
N2	0.000000	0.2800261	0.0000000	0.0000000	0.000000	0.0000000	0.000000	0.0000000
N3	0.000000	0.0000000	0.2882661	0.0000000	0.000000	0.0000000	0.000000	0.0000000
N4	0.000000	0.0000000	0.0000000	0.2221225	0.000000	0.0000000	0.000000	0.0000000
E1	0.000000	0.0000000	0.0000000	0.0000000	0.357039	0.0000000	0.000000	0.0000000
E2	0.000000	0.0000000	0.0000000	0.0000000	0.000000	0.3048445	0.000000	0.0000000
E3	0.000000	0.0000000	0.0000000	0.0000000	0.000000	0.0000000	0.376764	0.0000000
E4	0.000000	0.0000000	0.0000000	0.0000000	0.000000	0.0000000	0.000000	0.5113478

Mediante i parametri del modello la matrice di correlazione si riproduce nel modo seguente:

\[ \boldsymbol{\Sigma} =\boldsymbol{\Lambda} \boldsymbol{\Phi} \boldsymbol{\Lambda}^{\mathsf{T}} + \boldsymbol{\Psi}. \]

In \(\textsf{R}\) scriviamo:

R_hat <- lambda %*% Phi %*% t(lambda) + Psi
R_hat %>% 
  round(3)

A lavaan.matrix.symmetric: 8 × 8 of type dbl

	N1	N2	N3	N4	E1	E2	E3	E4
N1	1.000	0.751	0.746	0.780	-0.309	-0.321	-0.304	-0.269
N2	0.751	1.000	0.716	0.748	-0.296	-0.308	-0.291	-0.258
N3	0.746	0.716	1.000	0.744	-0.294	-0.306	-0.290	-0.257
N4	0.780	0.748	0.744	1.000	-0.308	-0.320	-0.303	-0.268
E1	-0.309	-0.296	-0.294	-0.308	1.000	0.669	0.633	0.561
E2	-0.321	-0.308	-0.306	-0.320	0.669	1.000	0.658	0.583
E3	-0.304	-0.291	-0.290	-0.303	0.633	0.658	1.000	0.552
E4	-0.269	-0.258	-0.257	-0.268	0.561	0.583	0.552	1.000

Le correlazioni residue sono:

(psychot_cor_mat - R_hat) %>% 
  round(3)

A lavaan.matrix.symmetric: 8 × 8 of type dbl

	N1	N2	N3	N4	E1	E2	E3	E4
N1	0.000	0.016	-0.015	-0.002	-0.042	0.005	0.008	-0.013
N2	0.016	0.000	-0.007	-0.010	-0.006	0.028	0.002	0.004
N3	-0.015	-0.007	0.000	0.018	-0.062	0.006	-0.007	-0.035
N4	-0.002	-0.010	0.018	0.000	-0.010	0.053	0.007	0.023
E1	-0.042	-0.006	-0.062	-0.010	0.000	0.006	0.001	-0.027
E2	0.005	0.028	0.006	0.053	0.006	0.000	-0.007	0.010
E3	0.008	0.002	-0.007	0.007	0.001	-0.007	0.000	0.014
E4	-0.013	0.004	-0.035	0.023	-0.027	0.010	0.014	0.000

Questo risultato riproduce ciò che abbiamo trovato estraendo la matrice di correlazioni residue dall’oggetto creato dal lavaan::cfa mediante l’istruzione residuals(fit2_cfa, type = "cor")$cov.

Per fare un esempio relativo alla correlazione tra due indicatori, calcoliamo la correlazione predetta dal modello tra le variabili \(Y_1\) e \(Y_2\):

lambda[1, 1] * lambda[2, 1] + lambda[1, 2] * lambda[2, 2] +
  lambda[1, 1] * lambda[2, 2] * Phi[1, 2] + 
  lambda[1, 2] * lambda[2, 1] * Phi[1, 2]

0.750782309575684

Questo valore si avvicina al valore contenuto dell’elemento (1, 2) della matrice di correlazioni osservate:

psychot_cor_mat[1, 2]

0.767

Usando le funzonalità di lavaan la matrice di correlazione predetta si ottiene con:

fitted(fit2_cfa)$cov |>
    print()

       N1     N2     N3     N4     E1     E2     E3     E4
N1  0.996                                                 
N2  0.748  0.996                                          
N3  0.743  0.713  0.996                                   
N4  0.777  0.745  0.741  0.996                            
E1 -0.307 -0.295 -0.293 -0.306  0.996                     
E2 -0.320 -0.306 -0.305 -0.319  0.666  0.996              
E3 -0.303 -0.290 -0.289 -0.302  0.630  0.656  0.996       
E4 -0.268 -0.257 -0.255 -0.267  0.558  0.580  0.550  0.996

La matrice dei residui è

resid(fit2_cfa)$cov |>
    print()

       N1     N2     N3     N4     E1     E2     E3     E4
N1  0.000                                                 
N2  0.016  0.000                                          
N3 -0.015 -0.007  0.000                                   
N4 -0.002 -0.010  0.018  0.000                            
E1 -0.042 -0.006 -0.062 -0.010  0.000                     
E2  0.005  0.028  0.006  0.053  0.006  0.000              
E3  0.008  0.002 -0.007  0.007  0.001 -0.007  0.000       
E4 -0.013  0.004 -0.035  0.023 -0.026  0.010  0.014  0.000

La matrice dei residui standardizzati è

resid(fit2_cfa, type = "standardized")$cov |>
    print()

       N1     N2     N3     N4     E1     E2     E3     E4
N1  0.000                                                 
N2  1.674  0.000                                          
N3 -1.769 -0.569  0.000                                   
N4 -0.350 -1.152  1.746  0.000                            
E1 -1.214 -0.161 -1.646 -0.294  0.000                     
E2  0.154  0.794  0.168  1.626  0.637  0.000              
E3  0.219  0.062 -0.191  0.193  0.075 -0.693  0.000       
E4 -0.314  0.092 -0.824  0.552 -1.481  0.624  0.690  0.000

I valori precedenti possono essere considerati come punti z, dove i valori con un valore assoluto maggiore di 2 possono essere ritenuti problematici. Tuttavia, è importante considerare che in questo modo si stanno eseguendo molteplici confronti, pertanto, si dovrebbe considerare l’opportunità di applicare una qualche forma di correzione per i confronti multipli.

## EFA con `lavaan`

Una funzionalità sperimentale di `lavaan` (ancora non ufficiale) è quella che consente di svolgere l'analisi fattoriale esplorativa con la funzione `efa()`. Consideriamo nuovamente i dati di @brown2015confirmatory, ovvero otto misure di personalità raccolte su un campione di 250 pazienti che hanno concluso un programma di psicoterapia.

Definiamo un modello ad un solo fattore comune.

# 1-factor model
f1 <- '
efa("efa")*f1 =~ N1 + N2 + N3 + N4 + E1 + E2 + E3 + E4
'

Definiamo un modello con due fattori comuni.

# 2-factor model
f2 <- '
efa("efa")*f1 +
efa("efa")*f2 =~ N1 + N2 + N3 + N4 + E1 + E2 + E3 + E4
'

Adattiamo ai dati il modello ad un fattore comune.

efa_f1 <-
  cfa(
    model = f1,
    sample.cov = psychot_cor_mat,
    sample.nobs = 250,
    rotation = "oblimin"
  )

Esaminiamo la soluzione ottenuta.

summary(
  efa_f1,
  fit.measures = TRUE,
  standardized = TRUE,
  rsquare = TRUE
) |>
  print()

lavaan 0.6.15 ended normally after 2 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        16

  Rotation method                      OBLIMIN OBLIQUE
  Oblimin gamma                                      0
  Rotation algorithm (rstarts)                GPA (30)
  Standardized metric                             TRUE
  Row weights                                     None

  Number of observations                           250

Model Test User Model:
                                                      
  Test statistic                               375.327
  Degrees of freedom                                20
  P-value (Chi-square)                           0.000

Model Test Baseline Model:

  Test statistic                              1253.791
  Degrees of freedom                                28
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.710
  Tucker-Lewis Index (TLI)                       0.594

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -2394.637
  Loglikelihood unrestricted model (H1)      -2206.974
                                                      
  Akaike (AIC)                                4821.275
  Bayesian (BIC)                              4877.618
  Sample-size adjusted Bayesian (SABIC)       4826.897

Root Mean Square Error of Approximation:

  RMSEA                                          0.267
  90 Percent confidence interval - lower         0.243
  90 Percent confidence interval - upper         0.291
  P-value H_0: RMSEA <= 0.050                    0.000
  P-value H_0: RMSEA >= 0.080                    1.000

Standardized Root Mean Square Residual:

  SRMR                                           0.187

Parameter Estimates:

  Standard errors                             Standard
  Information                                 Expected
  Information saturated (h1) model          Structured

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  f1 =~ efa                                                             
    N1                0.879    0.051   17.333    0.000    0.879    0.880
    N2                0.841    0.052   16.154    0.000    0.841    0.842
    N3                0.841    0.052   16.175    0.000    0.841    0.843
    N4                0.870    0.051   17.065    0.000    0.870    0.872
    E1               -0.438    0.062   -7.041    0.000   -0.438   -0.439
    E2               -0.398    0.063   -6.327    0.000   -0.398   -0.398
    E3               -0.398    0.063   -6.342    0.000   -0.398   -0.399
    E4               -0.364    0.063   -5.746    0.000   -0.364   -0.364

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .N1                0.224    0.028    7.915    0.000    0.224    0.225
   .N2                0.289    0.033    8.880    0.000    0.289    0.290
   .N3                0.288    0.032    8.866    0.000    0.288    0.289
   .N4                0.239    0.029    8.174    0.000    0.239    0.240
   .E1                0.804    0.073   10.963    0.000    0.804    0.807
   .E2                0.838    0.076   11.008    0.000    0.838    0.841
   .E3                0.837    0.076   11.007    0.000    0.837    0.841
   .E4                0.864    0.078   11.041    0.000    0.864    0.867
    f1                1.000                               1.000    1.000

R-Square:
                   Estimate
    N1                0.775
    N2                0.710
    N3                0.711
    N4                0.760
    E1                0.193
    E2                0.159
    E3                0.159
    E4                0.133

Adattiamo ai dati il modello a due fattori comuni.

efa_f2 <-
  cfa(
    model = f2,
    sample.cov = psychot_cor_mat,
    sample.nobs = 250,
    rotation = "oblimin"
  )

Esaminiamo la soluzione ottenuta.

summary(
  efa_f2,
  fit.measures = TRUE,
  standardized = TRUE,
  rsquare = TRUE
) |>
  print()

lavaan 0.6.15 ended normally after 1 iteration

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        23

  Rotation method                      OBLIMIN OBLIQUE
  Oblimin gamma                                      0
  Rotation algorithm (rstarts)                GPA (30)
  Standardized metric                             TRUE
  Row weights                                     None

  Number of observations                           250

Model Test User Model:
                                                      
  Test statistic                                 9.811
  Degrees of freedom                                13
  P-value (Chi-square)                           0.709

Model Test Baseline Model:

  Test statistic                              1253.791
  Degrees of freedom                                28
  P-value                                        0.000

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    1.000
  Tucker-Lewis Index (TLI)                       1.006

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -2211.879
  Loglikelihood unrestricted model (H1)      -2206.974
                                                      
  Akaike (AIC)                                4469.758
  Bayesian (BIC)                              4550.752
  Sample-size adjusted Bayesian (SABIC)       4477.840

Root Mean Square Error of Approximation:

  RMSEA                                          0.000
  90 Percent confidence interval - lower         0.000
  90 Percent confidence interval - upper         0.048
  P-value H_0: RMSEA <= 0.050                    0.957
  P-value H_0: RMSEA >= 0.080                    0.001

Standardized Root Mean Square Residual:

  SRMR                                           0.010

Parameter Estimates:

  Standard errors                             Standard
  Information                                 Expected
  Information saturated (h1) model          Structured

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  f1 =~ efa                                                             
    N1                0.874    0.053   16.592    0.000    0.874    0.876
    N2                0.851    0.055   15.551    0.000    0.851    0.853
    N3                0.826    0.054   15.179    0.000    0.826    0.828
    N4                0.896    0.053   16.802    0.000    0.896    0.898
    E1               -0.046    0.040   -1.138    0.255   -0.046   -0.046
    E2                0.035    0.034    1.030    0.303    0.035    0.035
    E3                0.000    0.040    0.010    0.992    0.000    0.000
    E4               -0.006    0.049   -0.131    0.896   -0.006   -0.006
  f2 =~ efa                                                             
    N1               -0.017    0.032   -0.539    0.590   -0.017   -0.017
    N2                0.011    0.035    0.322    0.748    0.011    0.011
    N3               -0.035    0.036   -0.949    0.343   -0.035   -0.035
    N4                0.031    0.031    0.994    0.320    0.031    0.031
    E1                0.776    0.059   13.125    0.000    0.776    0.778
    E2                0.854    0.058   14.677    0.000    0.854    0.855
    E3                0.785    0.060   13.106    0.000    0.785    0.787
    E4                0.695    0.063   10.955    0.000    0.695    0.697

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  f1 ~~                                                                 
    f2               -0.432    0.059   -7.345    0.000   -0.432   -0.432

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .N1                0.218    0.028    7.790    0.000    0.218    0.219
   .N2                0.279    0.032    8.693    0.000    0.279    0.280
   .N3                0.287    0.032    8.907    0.000    0.287    0.289
   .N4                0.216    0.029    7.578    0.000    0.216    0.217
   .E1                0.361    0.044    8.226    0.000    0.361    0.362
   .E2                0.292    0.043    6.787    0.000    0.292    0.293
   .E3                0.379    0.046    8.315    0.000    0.379    0.381
   .E4                0.509    0.053    9.554    0.000    0.509    0.511
    f1                1.000                               1.000    1.000
    f2                1.000                               1.000    1.000

R-Square:
                   Estimate
    N1                0.781
    N2                0.720
    N3                0.711
    N4                0.783
    E1                0.638
    E2                0.707
    E3                0.619
    E4                0.489

Anche se abbiamo introdotto finora soltanto la misura di bontà di adattamento del chi-quadrato, aggiungiamo qui il calcolo di altre misure di bontà di adattamento che discuteremo in seguito.

# define the fit measures
fit_measures_robust <- c(
  "chisq", "df", "pvalue", 
  "cfi", "rmsea", "srmr"
)

Confrontiamo le misure di bontà di adattamento del modello che ipotizza un solo fattore comune e il modello che ipotizza la presenza di due fattori comuni.

# collect them for each model
rbind(
  fitmeasures(efa_f1, fit_measures_robust),
  fitmeasures(efa_f2, fit_measures_robust)
) %>%
  # wrangle
  data.frame() %>%
  mutate(
    chisq = round(chisq, digits = 0),
    df = as.integer(df),
    pvalue = ifelse(pvalue == 0, "< .001", pvalue)
  ) %>%
  mutate_at(vars(cfi:srmr), ~ round(., digits = 3))

A data.frame: 2 × 6

chisq	df	pvalue	cfi	rmsea	srmr
<dbl>	<int>	<chr>	<dbl>	<dbl>	<dbl>
375	20	< .001	0.71	0.267	0.187
10	13	0.709310449320098	1.00	0.000	0.010

L’evidenza empirica supporta la superiorità del modello a due fattori rispetto a quello ad un solo fattore comune. In particolare, l’analisi fattoriale esplorativa svolta mediante la funzione efa() evidenzia la capacità del modello a due fattori di fornire una descrizione adeguata della struttura dei dati e di distinguere in modo sensato tra i due fattori ipotizzati.

Esercizio. Si utilizzino i dati dass21.txt che corrispondono alla somministrazione del test DASS-21 a 334 partecipanti. Lo schema di codifica si può trovare seguendo questo link. Si adatti ai dati un modello a tre fattori usando l’analisi fattoriale esplorativa con la funzione lavaan::efa(). Usando le saturazioni fattoriali e la matrice di inter-correlazioni fattoriali, si trovi la matrice di correlazioni riprodotta dal modello. Senza usare l’albebra matriciale, si trovi la correlazione predetta tra gli indicatori DASS-1 e DASS-2.