18. Il numero dei fattori#
L’analisi fattoriale esplorativa (EFA) rappresenta uno dei modelli statistici più impiegati in psicologia, risultando fondamentale per la validazione delle scale di misurazione, l’individuazione delle dimensioni latenti e la sintesi dei dati. Tuttavia, uno dei problemi principali nell’EFA riguarda la scelta del numero di fattori da considerare, poiché l’aggiunta di nuovi fattori può sempre migliorare l’adattamento ai dati, rendendo complesso definire un criterio statistico per determinare il numero ottimale di fattori.
La maggior parte dei metodi esistenti per selezionare il numero di fattori può essere diviso in due categorie.
I metodi della prima categoria analizzano gli autovalori della matrice di covarianza per determinare il numero di fattori.
La seconda categoria affronta la stima del numero di fattori come un problema di selezione di modelli. Poiché il modello fattoriale con il maggior numero di fattori si adatta sempre meglio ai dati, la stima del numero di fattori nella popolazione richiede un compromesso tra adattamento del modello e parsimonia della soluzione.
Esistono altri metodi oltre alle due categorie principali: il metodo Very Simple Structure (VSS) che cerca di recuperare strutture facilmente interpretabili e l’analisi grafica esplorativa (EGA) che stima una matrice di correlazione parziale regolarizzata e applica un algoritmo di rilevamento della comunità per determinare il numero di fattori.
18.1. Metodi basati sugli autovalori#
Sono stati proposti quattro criteri basati sugli autovalori per determinare il numero \(m\) di fattori da estrarre (Rencher, 2002).
Scegliere \(m\) tale per cui la varianza spiegata dal modello fattoriale superi una soglia predeterminata, per esempio l’80% della varianza totale, \(tr(\textbf{S})\) o \(tr(\textbf{R})\).
Scegliere \(m\) uguale al numero di autovalori aventi un valore maggiore del valore medio degli autovalori. Per R il valore medio degli autovalori è \(1\); per S è \(\sum_{j=1}^p \theta_j/p\).
Usare lo scree test.
Mediante la statistica \(\chi^2\), valutare l’ipotesi che \(m\) sia il numero corretto di fattori, \(H_0: \boldsymbol{\Sigma} = \boldsymbol{\Lambda} \boldsymbol{\Lambda}^{\mathsf{T}} + \boldsymbol{\Psi}\), dove \(\boldsymbol{\Lambda}\) è di ordine \(p \times m\).
18.1.1. Quota di varianza spiegata#
Il primo criterio si applica soprattutto al metodo delle componenti principali. La proporzione della varianza capionaria spiegata dal fattore \(j\)-esimo estratto da S è uguale a
Nel caso in cui i fattori vengano estratti da R avremo
Nel caso di fattori incorrelati, ciascun fattore contribuisce con una quota complessiva di varianza spiegata pari alla somma dei quadrati delle saturazioni fattoriali contenute nella matrice \(\hat{\boldsymbol{\Lambda}}\): \(\sum_{i=1}^p\sum_{j=1}^m\hat{\lambda}_{ij}^2\). Nel caso del metodo delle componenti principali, tale somma è anche uguale alla somma dei primi \(m\) autovalori, o alla somma di tutte le \(p\) comunalità:
Sulla base di queste considerazioni, il numero \(m\) di fattori viene scelto in modo da spiegare una quota sufficientemente grande di S o \(p\).
Il numero dei fattori può essere determinato in questo modo anche nel caso in cui l’analisi fattoriale venga eseguita con il metodo dei fattori principali (ovvero, nel caso in cui vengano usate le stime delle comunalità per generare la matrice ridotta \(\textbf{S} - \hat{\boldsymbol{\Psi}}\) o \(\textbf{R} - \hat{\boldsymbol{\Psi}}\)). In questo caso, però, è possibile che alcuni autovalori della matrice \(\textbf{S} - \hat{\boldsymbol{\Psi}}\) o \(\textbf{R} - \hat{\boldsymbol{\Psi}}\) assumano valore negativo. In tali circostanze, è possibile che la proporzione cumulativa della varianza \(\sum_{j=1}^m \theta_j / \sum_{j=1}^p \theta_j\) assuma un valore maggiore di \(1.0\) per \(j < p\).
La proporzione cumulativa della varianza si riduce poi a \(1.0\) quando vengono considerati anche i successivi autovalori negativi. Di conseguenza, può succedere che, utilizzando la matrice \(\textbf{S} - \hat{\boldsymbol{\Psi}}\) o \(\textbf{R} - \hat{\boldsymbol{\Psi}}\), il criterio definito in base alla quota della varianza spiegata venga raggiunto per un valore \(m\) minore di quello che verrebbe trovato utilizzando la matrice S o R.
Nel caso del metodo dei fattori principali iterato, \(m\) viene specificato precedentemente a ciascuna iterazione e \(\sum_{i} \hat{h}^2_i\) viene ottenuto dopo ciascuna iterazione calcolando \(\text{tr}(\textbf{S} - \hat{\boldsymbol{\Psi}})\). Per scegliere \(m\), come per il metodo delle componenti principali, possono essere usati gli autovalori di S o R.
18.1.2. Valore medio degli autovalori#
Il calcolo del valore medio degli autovalori è una procedura euristica implementata in molti software. In una variante di tale metodo, \(m\) viene scelto in modo tale da uguagliare il numero degli autovalori positivi della matrice ridotta \(\textbf{R} - \hat{\boldsymbol{\Psi}}\) (in tale matrice vi sono solitamente degli autovalori negativi). Tale variante ha però lo svantaggio di produrre solitamente un numero di fattori troppo grande.
18.1.3. Scree test#
Lo scree test si basa su un grafico che rappresenta gli autovalori di S o R ordinati in modo decrescente in funzione del numero dei fattori. I punti che rappresentano gli autovalori vengono collegati con una spezzata. Il valore m viene determinato in corrispondenza del fattore oltre il quale il dislivello tra fattori successivi diventa esiguo e la spezzata tende a diventare orizzontale.
18.1.4. Parallel analysis#
La Parallel Analysis si basa sul confronto tra gli autovalori empirici della matrice di correlazione delle variabili originali e quelli generati da un campione casuale di variabili standardizzate. In questo modo si tiene conto delle variazioni dovute agli errori di campionamento. Poiché anche in presenza di variabili incorrelate la matrice di correlazione presenta sempre autovalori maggiori di uno a causa della variabilità campionaria, il confronto tra gli autovalori empirici e quelli generati dalla Parallel Analysis permette di individuare il numero di fattori significativi. Una simulazione di Monte Carlo su una matrice di correlazione di \(p=10\) variabili casuali mutuamente indipendenti, ciascuna con \(n=20\) osservazioni, può essere utilizzata per illustrare la procedura.
n <- 20
nsim <- 1000
e1 <- rep(0, nsim)
for (i in 1:nsim) {
Y <- cbind(
rnorm(n), rnorm(n), rnorm(n), rnorm(n), rnorm(n),
rnorm(n), rnorm(n), rnorm(n), rnorm(n), rnorm(n)
)
e <- eigen(cor(Y))
e1[i] <- e$values[1]
}
max(e1)
Per i dati di questa simulazione, l’autovalore maggiore ha un valore pari a \(3.35\), anche se i dati sono del tutto casuali. La Parallel Analysis tiene conto di questo fatto e determina \(m\) confrontando gli autovalori empirici con le loro “controparti casuali.” Vanno a determinare \(m\) solo gli autovalori empirici che hanno un valore superiore ai corrispondenti autovalori generati da una matrice di dati dello stesso ordine composta da colonne mutualmente incorrelate. Nel caso di questa simulazione di Monte Carlo, se l’autovalore maggiore derivato da una matrice di numeri casuali ha un valore di \(3.35\), verranno considerati solo gli autovalori empirici che superano questo valore per determinare il numero di fattori.
18.2. Metodi basati sul confronto tra modelli#
Il confronto tra modelli può essere eseguito usando varie statistiche. Una scelta popolare per stimare il numero di fattori nella EFA è il Criterio d’Informazione Bayesiano (BIC; Schwarz, 1978), introdotto come un miglioramento rispetto al Criterio d’Informazione di Akaike (AIC; Akaike, 1973). Un’alternativa è l’indice RMSEA, che può essere considerato come una stima della mancanza di adattamento che tiene in considerazione i gradi di libertà del modello (Browne e Cudeck, 1992). Un altro metodo di questo tipo è il test Minimum Average Partial (MAP), che stima le correlazioni parziali residue medie per diversi numeri di fattori e seleziona quello con il valore più basso (Velicer, 1976).
18.2.1. Test del rapporto di verosimiglianze#
In questo test si confrontano due ipotesi: l’ipotesi nulla \(H_0\) e l’ipotesi alternativa \(H_1\), per valutare la bontà di adattamento di un modello fattoriale a una matrice di covarianza delle variabili oggetto di osservazione campionaria \(Y\). L’ipotesi nulla postula che la struttura di interdipendenza di \(Y\) può essere spiegata da \(m\) fattori comuni, mentre l’alternativa postula che i fattori comuni non sono sufficienti per spiegare la matrice di covarianza \(\boldsymbol{\Sigma}\).
Il test si basa sulla statistica del chi-quadrato con gradi di libertà pari a \(\nu = \frac{1}{2}[(p-m)^2-(p-m)]\), dove \(p\) è il numero di variabili e \(m\) è il numero di fattori. In pratica, si inizia con \(m^*=1\) e si valuta l’ipotesi \(H_0\) per \(m^*\). Se \(H_0\) non viene rifiutata, il procedimento si arresta. In caso contrario, si considera \(m^*+1\) e si ripete il test finché \(H_0\) viene accettata o finché si raggiunge il valore minimo di gradi di libertà pari a zero.
Il test del rapporto di verosimiglianze è particolarmente indicato quando il numero di osservazioni è grande, ma la sua applicazione è limitata dalle dimensioni del campione. In alternativa, è possibile utilizzare gli indici AIC, BIC e RMSEA per scegliere la soluzione con il valore più piccolo di tali statistiche. Tuttavia, questi indici non forniscono un test statistico per il confronto tra modelli.
In pratica, si può considerare il valore \(m\) indicato dal test come il limite superiore del numero di fattori che sono importanti dal punto di vista pratico.
18.2.2. Minimizzazione dell’out-of-sample prediction error#
Recentemente è stato proposto un nuovo metodo per stimare il numero di fattori in EFA che affronta il problema come un problema di selezione del modello [HvB22]. L’obiettivo è confrontare i modelli con 1, 2, …, p fattori, dove \(p\) è il numero di variabili, e selezionare il modello con l’errore di previsione atteso più basso nella popolazione. Tuttavia, questo è un compito non banale perché il modello che minimizza l’errore di previsione nel campione non minimizza sempre l’errore di previsione nella popolazione.
Intuitivamente, questo problema viene affrontato suddividendo il campione di dati in due insiemi: un set di training e un set di test. Il set di training viene utilizzato per stimare i parametri del modello, le cui previsioni vengono poi verificate utilizzando i dati di test (non utilizzati per la stima dei parametri). Questo calcolo dell’errore di previsione fuori campione viene ripetuto diverse volte, suddividendo ogni volta in modo casuale il campione negli insiemi di training e test. Tale metodo per stimare il numero di fattori è implementato nel pacchetto R fspe.
Esempio. Per confrontare i metodi discussi per la scelta del numero \(m\) di fattori usiamo una matrice di correlazioni calcolata sulle sottoscale della WAIS. Le 11 sottoscale del test sono le seguenti:
X1 = Information
X2 = Comprehension
X3 = Arithmetic
X4 = Similarities
X5 = Digit.span
X6 = Vocabulary
X7 = Digit.symbol
X8 = Picture.completion
X9 = Block.design
X10 = Picture.arrangement
X11 = Object.
I dati sono stati ottenuti dal manuale della III edizione.
varnames <- c(
"IN", "CO", "AR", "SI", "DS", "VO", "SY", "PC",
"BD", "PA", "OA", "AG", "ED"
)
temp <- matrix(c(
1, 0.67, 0.62, 0.66, 0.47, 0.81, 0.47, 0.60, 0.49, 0.51, 0.41,
-0.07, 0.66, .67, 1, 0.54, 0.60, 0.39, 0.72, 0.40, 0.54, 0.45,
0.49, 0.38, -0.08, 0.52, .62, .54, 1, 0.51, 0.51, 0.58, 0.41,
0.46, 0.48, 0.43, 0.37, -0.08, 0.49, .66, .60, .51, 1, 0.41,
0.68, 0.49, 0.56, 0.50, 0.50, 0.41, -0.19, 0.55, .47, .39, .51,
.41, 1, 0.45, 0.45, 0.42, 0.39, 0.42, 0.31, -0.19, 0.43,
.81, .72, .58, .68, .45, 1, 0.49, 0.57, 0.46, 0.52, 0.40, -0.02,
0.62, .47, .40, .41, .49, .45, .49, 1, 0.50, 0.50, 0.52, 0.46,
-0.46, 0.57, .60, .54, .46, .56, .42, .57, .50, 1, 0.61, 0.59,
0.51, -0.28, 0.48, .49, .45, .48, .50, .39, .46, .50, .61, 1,
0.54, 0.59, -0.32, 0.44, .51, .49, .43, .50, .42, .52, .52, .59,
.54, 1, 0.46, -0.37, 0.49, .41, .38, .37, .41, .31, .40, .46, .51,
.59, .46, 1, -0.28, 0.40, -.07, -.08, -.08, -.19, -.19, -.02,
-.46, -.28, -.32, -.37, -.28, 1, -0.29, .66, .52, .49, .55, .43,
.62, .57, .48, .44, .49, .40, -.29, 1
), nrow = 13, ncol = 13, byrow = TRUE)
colnames(temp) <- varnames
rownames(temp) <- varnames
wais_cor <- temp[1:11, 1:11]
wais_cor
| IN | CO | AR | SI | DS | VO | SY | PC | BD | PA | OA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| IN | 1.00 | 0.67 | 0.62 | 0.66 | 0.47 | 0.81 | 0.47 | 0.60 | 0.49 | 0.51 | 0.41 |
| CO | 0.67 | 1.00 | 0.54 | 0.60 | 0.39 | 0.72 | 0.40 | 0.54 | 0.45 | 0.49 | 0.38 |
| AR | 0.62 | 0.54 | 1.00 | 0.51 | 0.51 | 0.58 | 0.41 | 0.46 | 0.48 | 0.43 | 0.37 |
| SI | 0.66 | 0.60 | 0.51 | 1.00 | 0.41 | 0.68 | 0.49 | 0.56 | 0.50 | 0.50 | 0.41 |
| DS | 0.47 | 0.39 | 0.51 | 0.41 | 1.00 | 0.45 | 0.45 | 0.42 | 0.39 | 0.42 | 0.31 |
| VO | 0.81 | 0.72 | 0.58 | 0.68 | 0.45 | 1.00 | 0.49 | 0.57 | 0.46 | 0.52 | 0.40 |
| SY | 0.47 | 0.40 | 0.41 | 0.49 | 0.45 | 0.49 | 1.00 | 0.50 | 0.50 | 0.52 | 0.46 |
| PC | 0.60 | 0.54 | 0.46 | 0.56 | 0.42 | 0.57 | 0.50 | 1.00 | 0.61 | 0.59 | 0.51 |
| BD | 0.49 | 0.45 | 0.48 | 0.50 | 0.39 | 0.46 | 0.50 | 0.61 | 1.00 | 0.54 | 0.59 |
| PA | 0.51 | 0.49 | 0.43 | 0.50 | 0.42 | 0.52 | 0.52 | 0.59 | 0.54 | 1.00 | 0.46 |
| OA | 0.41 | 0.38 | 0.37 | 0.41 | 0.31 | 0.40 | 0.46 | 0.51 | 0.59 | 0.46 | 1.00 |
Il primo metodo per la determinazione di \(m\) richiede di estrarre tanti fattori quanti sono necessari per spiegare una quota predeterminata della varianza totale. Supponiamo di porre il criterio pari all’80% della varianza totale.
out <- eigen(wais_cor)
sum(out$val[1:4]) / sum(out$val)
sum(out$val[1:5]) / sum(out$val)
La soluzione ottenuta in questo modo ci porterebbe a mantenere \(m=5\) fattori.
Il secondo metodo suggerisce di mantenere tutti gli autovalori superiori al valore medio degli autovalori (che, nel caso di R è uguale a \(1\)).
print(round(out$values, 3))
[1] 6.074 1.015 0.746 0.587 0.508 0.431 0.423 0.377 0.351 0.310 0.177
Nel caso presente, \(m=2\).
Lo scree test può essere eseguito creando il grafico seguente.
n <- dim(wais_cor)[1]
scree_tb <- tibble(
x = 1:n,
y = sort(eigen(wais_cor)$value, decreasing = TRUE)
)
scree_plot <- scree_tb |>
ggplot(aes(x, y)) +
geom_point() +
geom_line() +
theme_minimal() +
scale_x_continuous(breaks = 1:n) +
ggtitle("Scree plot")
scree_plot
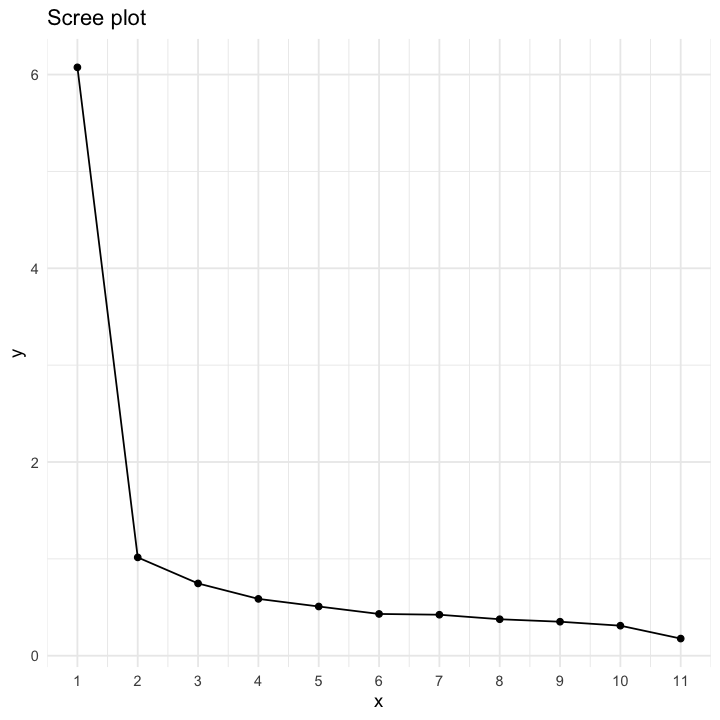
Lo scree test suggerisce la presenza di un unico fattore comune.
La versione della Parallel Analysis può essere eseguita con la funzione paran() contenuta nel pacchetto paran.
paran(wais_cor, graph = TRUE)
Using eigendecomposition of correlation matrix.
Computing: 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%
Results of Horn's Parallel Analysis for component retention
330 iterations, using the mean estimate
--------------------------------------------------
Component Adjusted Unadjusted Estimated
Eigenvalue Eigenvalue Bias
--------------------------------------------------
1 1.647667 3.765744 2.118077
--------------------------------------------------
Adjusted eigenvalues > 1 indicate dimensions to retain.
(1 components retained)
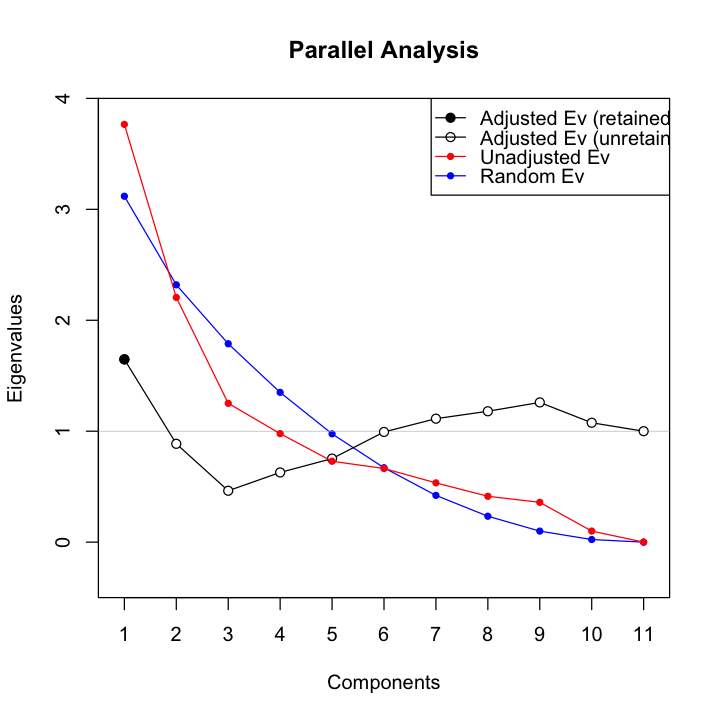
La Parallel Analysis indica una soluzione a \(m=1\) fattore.
Il test inferenziale relativo al numero di fattori basato sulla statistica \(\chi^2\) può essere eseguito nel modo seguente.
factanal(covmat=wais_cor, factors=4, n.obs=933)
factanal(covmat=wais_cor, factors=5, n.obs=933)
Call:
factanal(factors = 4, covmat = wais_cor, n.obs = 933)
Uniquenesses:
IN CO AR SI DS VO SY PC BD PA OA
0.229 0.387 0.005 0.416 0.645 0.137 0.005 0.375 0.331 0.492 0.519
Loadings:
Factor1 Factor2 Factor3 Factor4
IN 0.758 0.306 0.279 0.157
CO 0.672 0.312 0.229 0.107
AR 0.368 0.247 0.886 0.120
SI 0.602 0.376 0.193 0.207
DS 0.315 0.288 0.331 0.252
VO 0.851 0.242 0.208 0.192
SY 0.238 0.359 0.144 0.888
PC 0.432 0.623 0.143 0.172
BD 0.237 0.733 0.217 0.168
PA 0.367 0.539 0.150 0.245
OA 0.207 0.620 0.133 0.190
Factor1 Factor2 Factor3 Factor4
SS loadings 2.826 2.264 1.233 1.137
Proportion Var 0.257 0.206 0.112 0.103
Cumulative Var 0.257 0.463 0.575 0.678
Test of the hypothesis that 4 factors are sufficient.
The chi square statistic is 35.4 on 17 degrees of freedom.
The p-value is 0.00551
Call:
factanal(factors = 5, covmat = wais_cor, n.obs = 933)
Uniquenesses:
IN CO AR SI DS VO SY PC BD PA OA
0.235 0.389 0.117 0.419 0.600 0.109 0.277 0.308 0.334 0.472 0.456
Loadings:
Factor1 Factor2 Factor3 Factor4 Factor5
IN 0.745 0.264 0.301 0.192 0.118
CO 0.667 0.278 0.244 0.129 0.111
AR 0.378 0.236 0.814 0.145
SI 0.591 0.332 0.207 0.252 0.121
DS 0.288 0.208 0.366 0.341 0.155
VO 0.865 0.216 0.207 0.229
SY 0.251 0.364 0.153 0.708
PC 0.425 0.548 0.156 0.216 0.375
BD 0.246 0.708 0.230 0.201 0.107
PA 0.355 0.457 0.163 0.325 0.245
OA 0.211 0.664 0.128 0.205
Factor1 Factor2 Factor3 Factor4 Factor5
SS loadings 2.799 1.986 1.176 1.043 0.280
Proportion Var 0.254 0.181 0.107 0.095 0.025
Cumulative Var 0.254 0.435 0.542 0.637 0.662
Test of the hypothesis that 5 factors are sufficient.
The chi square statistic is 12.46 on 10 degrees of freedom.
The p-value is 0.256
Il test del \(\chi^2\) indica una soluzione a sei fattori.
Per concludere, si potrebbe usare il metodo basato sulla minimizzazione dell’errore di previsione. Tuttavia, non possiamo applicare tale metodo ai dati dell’esempio in quanto sarebbe necessario disporre dei dati grezzi (la matrice di correlazioni non è sufficiente). Allo scopo di illustrare la procedura relativa al metodo basato sulla minimizzazione dell’errore di previsione useremo qui un set di dati diverso, ovvero holzinger19.
data(holzinger19)
suppressWarnings(
fspe_out <- fspe(
data = holzinger19,
maxK = 10,
nfold = 10,
rep = 10,
method = "PE"
)
)
|
| | 0%
Loading required namespace: GPArotation
|
|------- | 10%
|
|-------------- | 20%
|
|--------------------- | 30%
|
|---------------------------- | 40%
par(mar=c(4,4,1,1))
plot.new()
plot.window(xlim=c(1, 10), ylim=c(.6, .8))
axis(1, 1:10)
axis(2, las=2)
abline(h=min(fspe_out$PEs), col="grey")
lines(fspe_out$PEs, lty=2)
points(fspe_out$PEs, pch=20, cex=1.5)
title(xlab="Number of Factors", ylab="Prediction Error")

Per i dati holzinger19, il metodo di Haslbeck and van Bork [HvB22] produce dunque una soluzione a 4 fattori.
18.3. Considerazioni conclusive#
In generale, la scelta del numero di fattori \(m\) non è sempre ovvia e rappresenta un limite dell’analisi fattoriale. Per affrontare questo problema, tradizionalmente si utilizza uno strumento come lo scree test per valutare la proporzione di varianza spiegata di ciascun item e l’interpretabilità della soluzione ottenuta dopo una rotazione adeguata. Tuttavia, poiché la scelta di \(m\) è soggettiva, i limiti della soluzione ottenuta sono evidenti. In alcuni casi, la scelta di \(m\) può essere più certa quando tutti i metodi forniscono la stessa risposta. Un’alternativa più moderna potrebbe essere l’uso di un metodo basato sulla minimizzazione dell’errore di previsione come quello descritto da Haslbeck and van Bork [HvB22]. In questo modo, si potrebbe ottenere una soluzione più affidabile e oggettiva.
