3. Fondamenti teorici#

3.1. Valutazione psicometrica come ragionamento inferenziale#

Inizialmente, i test psicometrici possono sembrare semplici strumenti di valutazione. Tuttavia, la valutazione psicologica e neuropsicologica va ben oltre l’assegnazione di punteggi. Questa pratica implica l’analisi delle osservazioni sul comportamento, le parole e le azioni delle persone per ottenere una comprensione più profonda di aspetti che non possono essere direttamente osservati. In particolare, la valutazione psicologica e neuropsicologica utilizza modelli probabilistici per formulare spiegazioni, previsioni e conclusioni.

Un secolo fa, la relazione tra le prestazioni osservate e l’abilità inosservabile del rispondente iniziò ad essere formalizzata in termini di errore di misurazione. Gulliksen [Gul61] descrisse il problema centrale della teoria dei test come la relazione tra l’abilità dell’individuo e il suo punteggio osservato sul test (p. 101). Questa caratterizzazione rimane valida ancora oggi, con una definizione adeguatamente ampia di “abilità” e “punteggio sul test” che possa comprendere le diverse forme di valutazione psicologica e neuropsicologica. Comprendere e rappresentare la relazione tra le prestazioni osservate e l’abilità soggiacente è quindi fondamentale per il ragionamento impiegato nella valutazione psicologica e neuropsicologica.

A causa dell’errore di misurazione, il ragionamento impiegato nella valutazione psicologica e neuropsicologica è un esempio di ragionamento in condizioni di incertezza. La natura imperfetta della misurazione e l’incompletezza delle informazioni disponibili rendono le nostre inferenze incerte e sempre soggette a revisione. Il passaggio dalle osservazioni parziali (ciò che vediamo un paziente dire, fare o produrre) alle conclusioni generali (la “vera” abilità del paziente) è necessariamente incerto e le nostre inferenze sono sempre soggette ad errori.

Per affrontare questa incertezza sulla relazione tra le prestazioni osservate e l’abilità soggiacente, molti progressi nella teoria psicometrica sono stati resi possibili trattando lo studio della relazione tra le risposte agli item di un test e il tratto ipotizzato di un individuo come un problema di inferenza statistica [Lew86]. [Sam83] ha anche proposto una connessione diretta tra errore di misura e approccio probabilistico, sostenendo che la natura complessa dei fattori che influenzano le reazioni di uno studente a uno stimolo rende necessario gestire la situazione in termini di relazione probabilistica tra i due.

Il punto di vista che sottolinea l’utilità di utilizzare il linguaggio e gli strumenti della teoria della probabilità per comunicare il carattere parziale dei dati e l’incertezza delle inferenze è diventato dominante nella psicometria moderna.

I reattivi psicologici possono essere costruiti e validati mediante vari approcci probabilistici, tra cui la Teoria Classica dei Test (CTT) e la Teoria di Risposta all’Item (IRT). Recentemente, il problema della valutazione psicologica è stato anche formulato in un’ottica bayesiana. In questo corso esamineremo la CTT e i suoi sviluppi più recenti.

3.2. La Teoria Classica#

La CTT nasce alla fine dell’Ottocento (Alfred Binet e altri, 1894) allo scopo di studiare l’attendibilità (o affidabilità) e la validità dei risultati dei questionari utilizzati per valutare le caratteristiche psico-sociali, non direttamente osservabili, delle persone esaminate.

Note

  • L’affidabilità è stata definita alternativamente come la correlazione al quadrato tra i punteggi veri e osservati (ad esempio, lord1968statistical, p. 61) o come il rapporto tra la varianza del punteggio vero di una scala e la sua varianza totale (ad esempio, McDonald, 1999). Queste definizioni sono matematicamente equivalenti quando la varianza del punteggio osservato è positiva, e entrambe presuppongono l’accesso alla varianza del punteggio vero di una scala. Poiché la varianza del punteggio vero è sconosciuta e può essere solo stimata dai dati osservati, la maggior parte delle stime di affidabilità si basa sull’assunzione che le covarianze osservate rappresentino necessariamente la varianza del punteggio vero.

  • La validità di un test psicometrico si riferisce alla misura in cui il test effettivamente misura ciò che si propone di misurare. La validità di un test è una valutazione della sua capacità di raggiungere i suoi obiettivi e può essere valutata attraverso una serie di evidenze empiriche. Alcuni tipi comuni di validità includono:

    1. Validità di contenuto: si riferisce al grado in cui il contenuto del test rappresenta adeguatamente il costrutto che si intende misurare.

    2. Validità di criterio: si riferisce al grado di associazione tra i punteggi del test e un criterio esterno che dovrebbe essere correlato al costrutto misurato. Può essere divisa in due sottocategorie:

      • Validità predittiva: si riferisce alla capacità del test di predire il comportamento o il risultato futuro correlato al costrutto in esame.

      • Validità concurrente: si riferisce alla correlazione tra i punteggi del test e il criterio esterno che è contemporaneamente misurato.

    3. Validità di costrutto: si riferisce alla capacità del test di misurare il costrutto o la caratteristica psicologica specifica che si intende valutare.

    4. Validità convergente e discriminante: si riferisce all’associazione del test con altre misure che dovrebbero essere correlate (validità di convergenza) o non correlate (validità di discriminazione) al costrutto misurato.

L’impiego su vasta scala e lo sviluppo della CTT ha inizio negli anni Trenta, anche se il modello formale su cui tale teoria si basa viene proposta da Spearman all’inizio del Novecento [Spe04]. La tecnica dell’analisi fattoriale esplorativa (Exploratory Factor Analysis, EFA), verrà poi affinata da Thurstone [Thu47] alla fine della seconda guerra mondiale. Tra la fine degli anni ‘60 e gli inizi degli anni ‘70, Jöreskog [Joreskog69] sviluppa l’analisi fattoriale confermativa (Confirmatory Factor Analysis, CFA). Negli anni ‘70, l’analisi fattoriale viene integrata con la path analysis nel lavoro di Jöreskog [Joreskog78] che dà origine ai modelli di equazioni strutturali (Structural Equation Modeling, SEM).

Iniziamo qui ad esaminare queste tecniche psicometriche prendendo in esame, per prima, la teoria classica dei test. Seguiremo la trattazione proposta da Lord and Novick [LN68].

L’equazione fondamentale alla quale si riconduce la teoria classica dei test è quella che ipotizza una relazione lineare e additiva tra il punteggio osservato di un test (\(X\)), la misura della variabile latente (\(T\)) e la componente casuale dell’errore (\(E\)). L’aspetto cruciale nella CTT riguarda la varianza dell’errore. Minore è la varianza dell’errore, più accuratamente il punteggio reale viene riflesso dai nostri punteggi osservati. In un mondo perfetto, tutti i valori di errore sarebbero uguali a 0. Cioè, ogni partecipante otterrebbe il punteggio esatto. Questo però non è possibile. Pertanto, abbiamo una certa varianza negli errori. La corrispondente deviazione standard di tali errori ha il un nome: si chiama errore standard di misurazione, indicato da \(\sigma_E\). Uno dei principali obiettivi della CTT è quello di ottenere una stima di \(\sigma_E\) in modo da potere valutare la qualità di una scala psicometrica.

3.3. Le due componenti del punteggio osservato#

CTT si occupa delle relazioni tra \(X\), \(T\) ed \(E\). La CTT si basa su un modello relativamente semplice in cui il punteggio osservato, il punteggio vero (cioè l’abilità inosservabile del rispondente) e l’errore aleatorio di misurazione sono legati da una relazione lineare. Indicati con \(T_{\nu j}\) (true score) l’abilità latente da misurare dell’individuo \(\nu\) nella prova \(j\), con \(X_{\nu j}\) la variabile osservata (observed score) per l’individuo \(\nu\) nella prova \(j\) e con \(E_{\nu j}\) l’errore aleatorio di misurazione, il modello è

(3.1)#\[ \begin{equation} X_{\nu j} = T_{\nu} + E_{\nu j}. \end{equation} \]

Dunque, in base all’eq. (3.1) il punteggio osservato \(X_{\nu j}\) differisce da quello vero \(T_{\nu j}\) a causa di una componente di errore casuale la quale viene assunta essere \(E_{\nu j} \sim \mathcal{N}(0, \sigma_E)\). Uno degli obiettivi centrali della CTT è quello di quantificare l’entità di tale errore (ovvero, di stimare \(\sigma_E\)). Vedremo come questa quantificazione verrà fornita in due forme: l’attendibilità del test e la stima dell’errore standard della misurazione. Si notino le similarità tra queste due misure della CTT e le misure di bontà di adattamento del modello di regressione lineare.

  • L’attendibilità (o affidabilità) rappresenta l’accuratezza con cui un test può misurare il punteggio vero (Coaley, 2014) e corrisponde al rapporto tra la varianza dei punteggi veri e la varianza dei punteggi osservati:

    • se l’attendibilità è grande, \(\sigma_E\) è piccolo – \(X\) ha un piccolo errore di misurazione e sarà vicino a \(T\).

    • se l’attendibilità è piccola, \(\sigma_E\) è grande – \(X\) presenta un grande errore di misurazione e si discosterà molto da \(T\).

  • La stima dell’errore standard della misurazione è una stima della deviazione standard della variabile casuale \(E\) (ovvero \(\sigma_E\)) che corrompe i punteggi veri.

Vedremo in seguito in che senso l’attendibilità della CTT possa essere messa in relazione con il coefficiente di determinazione del modello statistico della regressione lineare e come l’errore standard della misurazione della CTT possa essere messo in relazione con l’errore standard della regressione.

3.3.1. Il punteggio vero#

L’eq. (3.1) ci dice che il punteggio osservato è dato dalla somma di due componenti: una componente sistematica (il punteggio vero) e una componente aleatoria (l’errore di misurazione). Ma che cos’è il punteggio vero? CTT attribuisce diverse interpretazioni al punteggio vero.

  • La CTT considera un reattivo psicologico come una selezione casuale di item da un universo/popolazione di item attinenti al costrutto da misurare Nunnally [Nun94]; Kline [Kli13]. Se il reattivo psicologico viene concepito in questo modo, il punteggio vero diventa il punteggio che un rispondente otterrebbe se fosse misurato su tutto l’universo degli item del costrutto. In questo senso, l’errore di misurazione riflette il grado in cui gli item che costituiscono il test non riescono a rappresentare l’intero universo degli item attinenti al costrutto.

  • In maniera equivalente, il punteggio vero può essere concepito come il punteggio non “distorto” da componenti estranee al costrutto, ovvero da effetti di apprendimento, fatica, memoria, motivazione, eccetera. Essendo concepita come del tutto casuale (ovvero, priva di qualunque natura sistematica), la componente aleatoria non introduce alcun bias nella tendenza centrale della misurazione (la media di \(E\) viene assunta essere uguale a 0).

  • In termini puramente statistici, il punteggio vero è un punteggio inosservabile che corrisponde al valore atteso di infinite realizzazioni del punteggio ottenuto:

\[ T = \mathbb{E}(X) \equiv \mu_X \equiv \mu_{T}. \]

Combinando la seconda e la terza definizione presentate sopra, lord1968statistical concepiscono il punteggio vero come la media dei punteggi che un soggetto otterrebbe se il test venisse somministrato ripetutamente nelle stesse condizioni, in assenza di effetti di apprendimento e/o fatica.

3.3.2. Somministrazioni ripetute#

Nella formulazione del modello della CTT si possono distinguere due tipi di esperimenti aleatori: uno che considera l’unità di osservazione (l’individuo) come campionaria, l’altro che considera il punteggio, per un determinato individuo, come una variabile casuale. Un importante risultato è dato dall’unione di questi due esperimenti casuali, ovvero dalla dimostrazione che i risultati della CTT, la quale è stata sviluppata ipotizzando ipotetiche somministrazioni ripetute del test allo stesso individuo sotto le medesime condizioni, si generalizzano al caso di una singola somministrazione del test ad un campione di individui [AY01]. In base a questo risultato, se consideriamo la somministrazione del test ad una popolazione di individui, allora diventa più facile assegnare un contenuto empirico alle quantità discusse dalla CTT:

  • \(\sigma^2_X\) è la varianza del punteggio osservato nella popolazione,

  • \(\sigma^2_T\) è la varianza dei punteggio vero nella popolazione,

  • \(\sigma^2_E\) è la varianza della componente d’errore nella popolazione.

3.3.3. Le assunzioni sul punteggio ottenuto#

La CTT assume che la media del punteggio osservato \(X\) sia uguale alla media del punteggio vero,

(3.2)#\[ \mu_X \equiv \mu_{T}, \]

in altri termini, assume che il punteggio osservato fornisca una stima statisticamente corretta dell’abilità latente (punteggio vero).

In pratica, il punteggio osservato non sarà mai uguale all’abilità latente, ma corrisponde solo ad uno dei possibili punteggi che il soggetto può ottenere, subordinatamente alla sua abilità latente. L’errore della misura è la differenza tra il punteggio osservato e il punteggio vero:

\[E \equiv X - T.\]

In base all’assunzione secondo cui il valore atteso dei punteggi è uguale alla media del valore vero, segue che

\[ \mathbb{E}(E) = \mathbb{E}(X - T) = \mathbb{E}(X) - \mathbb{E}(T) = \mu_{T} - \mu_{T} = 0, \]

ovvero, il valore atteso degli errori è uguale a zero.

3.4. L’errore standard della misurazione \(\sigma_E\)#

La radice quadrata della varianza degli errori di misurazione, ovvero la deviazione standard degli errori, \(\sigma_E\), è la quantità fondamentale della CTT ed è chiamata errore standard della misurazione. La stima dell’errore standard della misurazione costituisce uno degli obiettivi più importanti della CTT.

Ricordiamo che la deviazione standard indica quanto i dati di una distribuzione si discostano dalla media di quella distribuzione. È simile allo scarto tipico, ovvero la distanza media tra i valori della distribuzione e la loro media. Possiamo dunque utilizzare questa proprietà per descrivere il modo in cui la CTT interpreta la quantità \(\sigma_E\): l’errore standard della misurazione \(\sigma_E\) ci dice qual è, approssimativamente, la quantità attesa di variazione del punteggio osservato, se il test venisse somministrato ripetute volte al medesimo rispondente sotto le stesse condizioni (ovvero, in assenza di effetti di apprendimento o di fatica).

3.5. Assiomi della Teoria Classica#

La CTT assume che gli errori siano delle variabili casuali incorrelate tra loro

\[ \rho(E_i, E_k \mid T) = 0, \qquad\text{con}\; i \neq k, \]

e incorrelate con il punteggio vero,

\[ \rho(E, T) = 0, \]

le quali seguono una distribuzione gaussiana con media zero e deviazione standard pari a \(\sigma_E\):

\[ E \sim \mathcal{N}(0, \sigma_E). \]

La quantità \(\sigma_E\) è appunto l’errore standard della misurazione. Sulla base di tali assunzioni la CTT deriva la formula dell’attendibilità di un test.

Si noti che le assunzioni della CTT hanno una corrispondenza puntuale con le assunzioni su cui si basa il modello di regressione lineare.

3.6. L’attendibilità del test#

In questa sezione vedremo come il coefficiente di attendibilità (altri termini che vengono usati sono: affidabilità, costanza, credibilità) fornisce una stima della quota della varianza del punteggio osservato che può essere attribuita all’abilità latente (“punteggio vero”, cioè privo di errore di misurazione). In generale, un coefficiente di attendibilità maggiore di 0.80 viene ritenuto soddisfacente perché indica che l’80% o più della varianza dei punteggi ottenuti è causata da ciò che il test intende misurare, anziché dall’errore di misurazione.

Per definire l’attendibilità, la CTT si serve di due quantità:

  • la varianza del punteggio osservato,

  • la correlazione tra punteggio osservato e punteggio vero.

Vediamo ora come queste quantità possano essere ottenute sulla base delle assunzioni del modello statistico che sta alla base della CTT.

3.6.1. La varianza del punteggio osservato#

La varianza del punteggio osservato \(X\) è uguale alla somma della varianza del punteggio vero e della varianza dell’errore di misurazione:

(3.3)#\[ \sigma^2_X = \sigma_T^2 + \sigma_E^2. \]

Proof. La varianza del punteggio osservato è uguale a

(3.4)#\[ \sigma^2_X = \mathbb{V}(T+E) = \sigma_T^2 + \sigma_E^2 + 2 \sigma_{TE}. \]

Dato che \(\sigma_{TE}=\rho_{TE}\sigma_T \sigma_E=0\), in quanto \(\rho_{TE}=0\), ne segue che

\[ \sigma^2_X = \sigma_T^2 + \sigma_E^2. \]

3.6.2. La covarianza tra punteggio osservato e punteggio vero#

La covarianza tra punteggio osservato \(X\) e punteggio vero \(T\) è uguale alla varianza del punteggio vero:

(3.5)#\[ \sigma_{X T} = \sigma_T^2. \]

Proof. La covarianza tra punteggio osservato e punteggio vero è uguale a

\[\begin{split} \begin{aligned} \sigma_{X T} &= \mathbb{E}(XT) - \mathbb{E}(X)\mathbb{E}(T)\notag\\ &= \mathbb{E}[(T+E)T] - \mathbb{E}(T+E)\mathbb{E}(T)\notag\\ &= \mathbb{E}(T^2) + \underbrace{\mathbb{E}(ET)}_{=0} - [\mathbb{E}(T)]^2 - \underbrace{\mathbb{E}(E)}_{=0} \mathbb{E}(T)\notag\\ &=\mathbb{E}(T^2) - [\mathbb{E}(T)]^2\notag \\ &= \sigma_T^2. \end{aligned} \end{split}\]

3.6.3. Correlazione tra punteggio osservato e punteggio vero#

La correlazione tra punteggio osservato \(X\) e punteggio vero \(T\) è uguale al rapporto tra la covarianza tra \(X\) e \(T\) divisa per il prodotto delle due deviazioni standard:

(3.6)#\[ \rho_{XT} = \frac{\sigma_{XT}}{\sigma_X \sigma_T} = \frac{\sigma^2_{T}}{\sigma_X \sigma_T} = \frac{\sigma_{T}}{\sigma_X}. \]

Dunque, la correlazione tra il punteggio osservato e il punteggio vero è uguale al rapporto tra la deviazione standard dei punteggi veri e la deviazione standard dei punteggi osservati.

3.6.4. Definizione e significato dell’attendibilità#

Sulla base della eq-sd-ratio giungiamo alla definizione dell’attendibilità. La CTT definisce attendibilità di un test (o di un item) come il rapporto tra la varianza del punteggio vero e la varianza del punteggio osservato, ovvero come il quadrato della correlazione tra punteggio osservato \(X\) e punteggio vero \(T\):

(3.7)#\[ \begin{equation} \rho_{XT}^2 = \frac{\sigma_{T}^2}{\sigma_X^2}. \end{equation} \]

Questa è la quantità fondamentale della CTT e misura il grado di variazione del punteggio vero rispetto alla variazione del punteggio osservato. Dato che \(\sigma^2_X = \sigma_T^2 + \sigma_E^2\), in base alla eq-reliability-1 possiamo scrivere

(3.8)#\[ \begin{equation} \rho_{XT}^2 = \frac{\sigma_{T}^2}{\sigma_X^2} =\frac{\sigma_{X}^2 - \sigma^2_E}{\sigma_X^2} = 1-\frac{\sigma_{E}^2}{\sigma_X^2}. \end{equation} \]

La (3.8) ci dice che il coefficiente di attendibilità assume valore \(1\) se la varianza degli errori \(\sigma_{E}^2\) è nulla e assume valore \(0\) se la varianza degli errori è uguale alla varianza del punteggio osservato. Il coefficiente di attendibilità è dunque un numero puro contenuto nell’intervallo compreso tra \(0\) e \(1\).

3.7. Attendibilità e modello di regressione lineare#

In parole semplici, la CTT (Teoria Classica dei Test) si basa sul modello di regressione lineare, dove i punteggi osservati sono considerati come variabile dipendente e i punteggi veri come variabile indipendente. Il coefficiente di attendibilità \(\rho_{XT}^2\) rappresenta la proporzione di varianza nella variabile dipendente spiegata dalla variabile indipendente in un modello di regressione lineare con una pendenza unitaria e un’intercetta di zero. In altre parole, il coefficiente di attendibilità è equivalente al coefficiente di determinazione del modello di regressione.

3.7.1. Simulazione#

Per dare un contenuto concreto alle affermazioni precedenti, consideriamo la seguente simulazione svolta in \(\textsf{R}\). In tale simulazione il punteggio vero \(T\) e l’errore \(E\) sono creati in modo tale da soddisfare i vincoli della CTT: \(T\) e \(E\) sono variabili casuali gaussiane tra loro incorrelate. Nella simulazione generiamo 100 coppie di valori \(X\) e \(T\) con i seguenti parametri: \(T \sim \mathcal{N}(\mu_T = 12, \sigma^2_T = 6)\), \(E \sim \mathcal{N}(\mu_E = 0, \sigma^2_T = 3)\):

set.seed(12345)
library("MASS")

n <- 100
Sigma <- matrix(c(6, 0, 0, 3), byrow = TRUE, ncol = 2)
Sigma
mu <- c(12, 0)
mu
Y <- mvrnorm(n, mu, Sigma, empirical = TRUE)
T <- Y[, 1]
E <- Y[, 2]

Attaching package: ‘MASS’

The following object is masked from ‘package:patchwork’:

    area

The following object is masked from ‘package:dplyr’:

    select
A matrix: 2 × 2 of type dbl
60
03
  1. 12
  2. 0

Le istruzioni precedenti (empirical = TRUE) creano un campione di valori nei quali le medie e la matrice di covarianze assumono esattamente i valori richiesti. Possiamo dunque immaginare tale insieme di dati come la “popolazione”.

Secondo la CTT, il punteggio osservato è \(X = T + E\). Simuliamo dunque il punteggio osservato \(X\) come:

X <- T + E

Le prime 6 osservazioni così ottenute sono:

head(cbind(T, E, X))
A matrix: 6 × 3 of type dbl
TEX
12.825569-0.0501994812.775370
11.888097 2.2613869014.149484
11.622652-0.8558436110.766808
9.445738 1.7202317511.165970
12.794828 0.0975796312.892407
7.425294-0.50493930 6.920355

Un diagramma di dispersione è fornito nella figura seguente:

tibble(X, T) %>%
  ggplot(aes(X, T)) +
  geom_point()
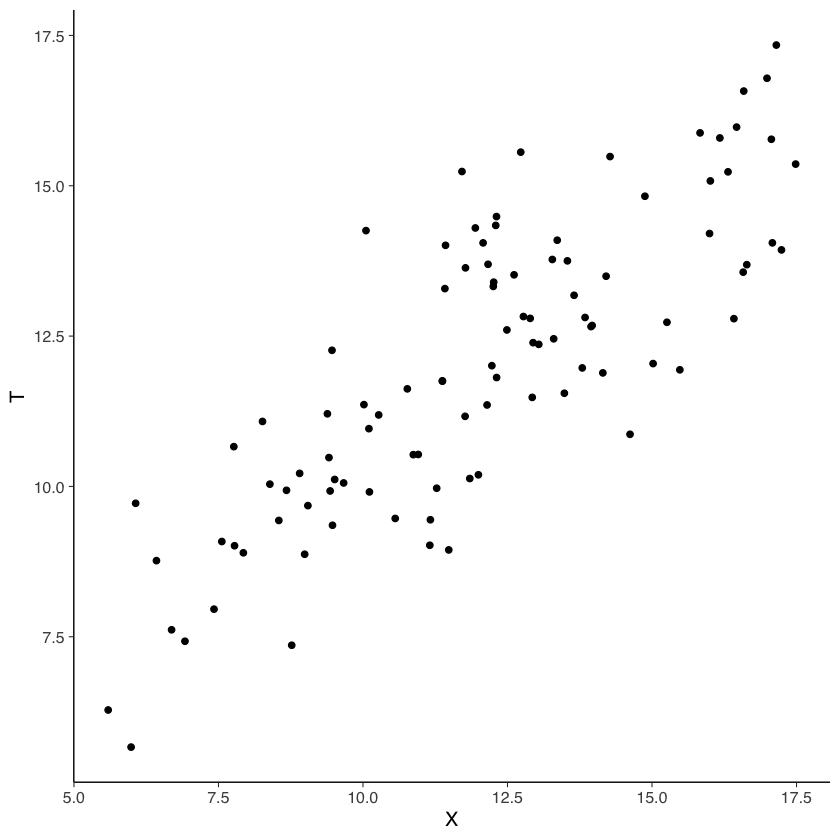
_images/36de510aa33431d8fa8f6c77c9e22cc00cc0152eea2d84ea628c26a2a1f1232c.png

Secondo la CTT, il valore atteso di \(T\) è uguale al valore atteso di \(X\). Verifichiamo questa assunzione nei nostri dati:

mean(T)
mean(X)
12
12

L’errore deve avere media zero, varianza \(\sigma_E^2\) e deve essere incorrelato con \(T\):

mean(E)
var(E)
cor(T, E)
9.27394012278926e-17
3
-1.53436207573137e-16

Ricordiamo che la radice quadrata della varianza degli errori è l’errore standard della misurazione, \(\sigma_E\). La quantità \(\sqrt{\sigma_E^2}\) fornisce una misura della dispersione del punteggio osservato attorno al valore vero, nella condizione ipotetica di ripetute somministrazioni del test:

sqrt(3)
1.73205080756888

Dato che \(T\) e \(E\) sono incorrelati, ne segue che la varianza del punteggio osservato \(X\) è uguale alla somma della varianza del punteggio vero \(T\) e della varianza degli errori \(E\):

var(X)
var(T) + var(E)
9
9

La varianza del punteggio vero \(T\) è uguale alla covarianza tra il punteggio vero \(T\) e il punteggio osservato \(X\):

var(T)
cov(T, X)
6
6

La correlazione tra punteggio osservato e punteggio vero è uguale al rapporto tra la deviazione standard del punteggio vero e la deviazione standard del punteggio osservato:

cor(X, T)
sd(T) / sd(X)
0.816496580927726
0.816496580927726

Per la CTT, l’attendibilità è uguale al quadrato del coefficiente di correlazione tra il punteggio vero \(T\) e il punteggio osservato \(X\), ovvero:

cor(X, T)^2
0.666666666666666

La motivazione di questa simulazione è quella di mettere in relazione il coefficiente di attendibilità, calcolato con la formula della CTT (come abbiamo fatto sopra), con il modello di regressione lineare. Analizziamo dunque i dati della simulazione mediante il seguente modello di regressione lineare:

\[ X = a + b T + E. \]

Usando \(\textsf{R}\) otteniamo:

fm <- lm(X ~ T)
summary(fm)

Call:
lm(formula = X ~ T)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.2022 -1.0875 -0.0178  1.1394  3.7528 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 2.842e-15  8.746e-01       0        1    
T           1.000e+00  7.143e-02      14   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.741 on 98 degrees of freedom
Multiple R-squared:  0.6667,	Adjusted R-squared:  0.6633 
F-statistic:   196 on 1 and 98 DF,  p-value: < 2.2e-16

Si noti che la retta di regressione ha intercetta 0 e pendenza 1. Questo è coerente con l’assunzione \(\mathbb{E}(X) = \mathbb{E}(T)\). Ma il risultato più importante di questa simulazione è che il coefficiente di determinazione (\(R^2\) = 0.67) del modello di regressione \(X = 0 + 1 \times T + E\) è identico al coefficiente di attendibilità calcolato con la formula \(\rho_{XT}^2 = \frac{\sigma_{T}^2}{\sigma_X^2}\):

var(T) / var(X)
0.666666666666667

Ciò ci consente di interpretare il coefficiente di attendibilità nel modo seguente: l’attendibilità di un test non è altro che la quota di varianza del punteggio osservato \(X\) che viene spiegata dalla regressione di \(X\) sul punteggio vero \(T\) in un modello di regressione lineare dove \(\alpha\) = 0 e \(\beta\) = 1.

3.8. Misurazioni parallele e affidabilità#

L’equazione \(\rho_{XT}^2 = \frac{\sigma_{T}^2}{\sigma_X^2}\) definisce il coefficiente di attendibilità ma non ci fornisce gli strumenti per calcolarlo in pratica, dato che la varianza del punteggio vero \(\sigma_{T}^2\) è una quantità incognita. Il metodo utilizzato dalla CTT per ottenere una stima empirica dell’attendibilità è quello delle forme parallele del test: se è possibile elaborare versioni alternative dello stesso test che risultino equivalenti tra loro in termini di contenuto, modalità di risposta e caratteristiche statistiche, allora diventa anche possibile stimare il coefficiente di attendibilità.

Secondo la CTT, due test \(X=T+E\) e \(X^\prime=T^\prime+E^\prime\) si dicono misurazioni parallele della stessa abilità latente se

  • \(T = T^\prime\),

  • \(\mathbb{V}(E) = \mathbb{V}(E^\prime)\).

Da tali assunzioni segue che \(\mathbb{E}(X) = \mathbb{E}(X^\prime)\).

Proof. Dato che \(\mathbb{E}(X) = T\) e che \(\mathbb{E}(X^\prime) = T\), è immediato vedere che \(\mathbb{E}(X) =\mathbb{E}(X^\prime)\) in quanto \(\mathbb{E}(E) = \mathbb{E}(E^\prime) = 0\).

In maniera corrispondente, anche le varianze dei punteggi osservati di due misurazioni parallele devono essere uguali, \(\mathbb{V}(X) = \mathbb{V}(X^\prime)\).

Proof. Per \(X\) abbiamo che \(\mathbb{V}(X) = \mathbb{V}(T + E) = \mathbb{V}(T) + \mathbb{V}(E)\); per \(X^\prime\) abbiamo che \(\mathbb{V}(X^\prime) = \mathbb{V}(T^\prime + E^\prime) = \mathbb{V}(T^\prime) + \mathbb{V}(E^\prime)\). Dato che \(\mathbb{V}(E) = \mathbb{V}(E^\prime)\) e che \(T = T^\prime\), ne segue che \(\mathbb{V}(X) = \mathbb{V}(X^\prime)\).

Per costruzione, inoltre, gli errori \(E\) e \(E^\prime\) devono essere incorrelati con \(T\) e tra loro.

3.8.1. La correlazione tra due forme parallele del test#

Dimostriamo ora che, in base alle assunzioni della CTT, la correlazione tra due forme parallele del test è uguale al rapporto tra la varianza del punteggio vero e la varianza del punteggio osservato.

Proof. Assumendo, senza perdita di generalità, che \(\mathbb{E}(X)=\mathbb{E}(X')=\mathbb{E}(T)=0\), possiamo scrivere

\[\begin{split} \begin{equation} \begin{aligned} \rho_{X X^\prime} &= \frac{\sigma(X, X^\prime)}{\sigma(X) \sigma(X^\prime)}\notag\\ &= \frac{\mathbb{E}(XX^\prime)}{\sigma(X) \sigma(X^\prime)}\notag\\ &=\frac{\mathbb{E}[(T+E)(T+E^\prime)]}{\sigma(X) \sigma(X^\prime)}\notag\\ &=\frac{\mathbb{E}(T^2)+\mathbb{E}(TE^\prime)+\mathbb{E}(TE)+ \mathbb{E}(EE^\prime)}{\sigma(X) \sigma(X^\prime)}.\notag \end{aligned} \end{equation} \end{split}\]

Ma \(\mathbb{E}(TE) = \mathbb{E}(TE^\prime) = \mathbb{E}(EE^\prime)=0\). Inoltre, \(\sigma(X) =\sigma(X^\prime)= \sigma_X\). Dunque,

\[ \begin{equation} \rho_{X X^\prime} =\frac{\mathbb{E}(T^2)}{\sigma_X \sigma_X} = \frac{\sigma^2_T}{\sigma^2_X}. (\#eq:3-3-5) \end{equation} \]

Si noti come la @ref(eq:3-3-5) e l’equazione che definisce il coefficiente di attendibilità, ovvero \(\rho_{XT}^2 = \frac{\sigma_{T}^2}{\sigma_X^2}\), riportano tutte e due la stessa quantità a destra dell’uguale. Otteniamo così un importante risultato: il coefficiente di attendibilità, ovvero il quadrato del coefficiente di correlazione tra il punteggio osservato e il punteggio vero, è uguale alla correlazione tra il valore osservato di due misurazioni parallele:

(3.9)#\[ \begin{equation} \rho^2_{XT} = \rho_{XX^\prime}. \end{equation} \]

Tale risultato è importante perché consente di esprimere la quantità inosservabile \(\rho^2_{XT}\) nei termini della quantità \(\rho_{XX^\prime}\) che può essere calcolata sulla base dei punteggi osservati di due forme parallele del test. Quindi, la stima di \(\rho^2_{XT}\) si riduce alla stima di \(\rho^2_{XX^\prime}\). Per questa ragione, la {}ref{eq-rho2xt-rhoxx} è forse la formula più importante della CTT. Inoltre, è importante notare che l’eq. eq:rho2xt-rhoxx fornisce la giustificazione per l’utilizzo della correlazione split-half come misura di attendibilità.

3.8.2. La correlazione tra punteggio osservato e punteggio vero#

Consideriamo ora la correlazione tra punteggio osservato e punteggio vero. La eq-rho2xt-rhoxx si può scrivere come

\[ \rho_{XT} = \sqrt{\rho_{XX^\prime}}. \]

In altri termini: la radice quadrata del coefficiente di attendibilità è uguale alla correlazione tra il punteggio osservato e il punteggio vero.

3.8.3. I fattori che influenzano l’attendibilità#

Considerando le tre equazioni

\[ \rho^2_{XT} = \rho_{XX'},\quad \rho_{XT}^2 = \frac{\sigma_{T}^2}{\sigma_X^2}, \quad \rho_{XT}^2 = 1-\frac{\sigma_{E}^2}{\sigma_X^2}, \]

possiamo dire che ci sono tre modi equivalenti per concludere che l’attendibilità di un test è alta. La attendibilità di un test è considerata alta se si verificano le seguenti condizioni:

-La correlazione tra le forme parallele del test è alta.

  • La varianza del punteggio vero è grande rispetto alla varianza del punteggio osservato.

  • La varianza dell’errore di misura è piccola rispetto alla varianza del punteggio osservato.

Queste considerazioni sono importanti per la progettazione di un test. In particolare, l’equazione \(\rho^2_{XT} = \rho_{XX'}\) fornisce un criterio per la selezione degli item da includere nel test. Se interpretiamo \(\rho_{XX'}\) come la correlazione tra due item, allora gli item che hanno la correlazione più alta tra di loro dovrebbero essere inclusi nel test. In questo modo, l’attendibilità del test aumenta perché gli item inclusi sono maggiormente correlati con il punteggio vero.

3.9. Metodi alternativi per la stima del coefficiente di attendibilità#

In pratica, come si stima l’affidabilità di un test? Per stimare l’affidabilità di un test, esistono diversi metodi. Uno di questi consiste nella somministrazione dello stesso test a un gruppo di individui in due momenti diversi, in modo da calcolare la correlazione dei punteggi totali ottenuti (test-retest reliability).Questo metodo può essere giustificato in due modi diversi mcdonald2013test.

  • Il primo si basa sull’assunzione che il valore vero non varia tra le due somministrazioni del test. In tal caso, gli errori commessi dai partecipanti durante le due somministrazioni sono indipendenti tra loro e la correlazione tra i punteggi totali ci fornisce una stima del coefficiente di correlazione tra gli item del test. Tuttavia, non è possibile distinguere questa situazione ideale dal caso in cui viene violata l’assunzione di invarianza del punteggio vero.

  • Il secondo metodo si basa sulla definizione del punteggio vero di retest come la componente del punteggio osservato che non varia tra le due somministrazioni. In questo caso, il coefficiente di attendibilità viene concepito come un coefficiente di stabilità temporale, che diminuisce all’aumentare dell’intervallo di tempo tra le due somministrazioni.

Il metodo test-retest ha il limite di fornire solo un sottoinsieme delle informazioni che verrebbero raccolte da uno studio longitudinale che copre un periodo di tempo maggiore. Se fosse possibile eseguire uno studio di questo tipo, potremmo trovare la funzione che descrive la variazione del punteggio osservato in funzione del tempo. In generale, tale funzione non può essere descritta da un singolo parametro. Resta dunque aperta la domanda di quale sia relazione tra questa funzione e il coefficiente di attendibilità.

Se sono disponibili due forme parallele dello stesso test, l’affidabilità può essere calcolata mediante il coefficiente di correlazione dei punteggi totali dei due test (parallel-forms reliability), valendo l’uguaglianza \(\rho_{XX^\prime} = \rho^2_{XT}\). Anche questo metodo, come il metodo del test-retest, non è esente da errori.

Il metodo di stima più diffuso è quello dell’attendibilità come consistenza interna (internal consistency reliability), originariamente ricavato da Kuder and Richardson [KR37] per item dicotomici e poi generalizzato da Cronbach [Cro51] per item a risposte ordinali. L’idea su cui si basa consiste nel fatto che ogni singolo item del test, se confrontato con tutti gli altri, può essere usato per stimare l’affidabilità del test. L’analisi degli item valuta dunque quanto gli item del test misurano lo stesso costrutto.