6  Variabili casuali

Introduzione

Finora abbiamo studiato le probabilità di eventi discreti, come vincere il gioco di Monty Hall o ricevere una diagnosi medica accurata. Tuttavia, molte situazioni pratiche richiedono una comprensione più sottile e quantitativa dell’incertezza. Invece di chiederci semplicemente se qualcosa accadrà, spesso abbiamo bisogno di sapere con quale frequenza accadrà, per quanto tempo durerà o quale valore numerico possiamo aspettarci.

Per esempio, potremmo voler determinare quanti tentativi sono necessari prima che un concorrente vinca in uno scenario simile a quello del gioco di Monty Hall o stimare la durata attesa di un trattamento medico. Allo stesso modo, giocando per molte ore con un dado sbilanciato, potremmo essere interessati a calcolare la perdita finanziaria media che possiamo aspettarci nel lungo periodo.

Queste domande richiedono un approccio più sofisticato rispetto alla semplice valutazione della probabilità di eventi isolati. Implicano la quantificazione di risultati numerici che emergono da processi casuali. Per affrontare in modo sistematico questo tipo di problemi, introduciamo il concetto fondamentale di variabile casuale.

Una variabile casuale è, in sostanza, una funzione che associa un valore numerico a ogni possibile risultato di un esperimento casuale. Questo potente strumento matematico ci permette di tradurre l’incertezza qualitativa in quantità misurabili e di calcolare valori attesi, varianze e altre caratteristiche distributive. Grazie alle variabili casuali, possiamo non solo prevedere se un evento si verificherà, ma anche come si manifesterà numericamente quando si verifica.

In questo capitolo esploreremo le proprietà fondamentali delle variabili casuali, gettando le basi per affrontare le questioni pratiche che richiedono una comprensione quantitativa del comportamento aleatorio nei sistemi complessi.

Panoramica del capitolo

• Le definizioni e le caratteristiche delle variabili casuali discrete e continue, e le relative distribuzioni di probabilità.
• Come calcolare e interpretare il valore atteso di variabili casuali, sia discrete che continue.
• Determinare e comprendere la varianza e la deviazione standard di variabili casuali.

ConsiglioPrerequisiti

Per seguire al meglio questo capitolo, è consigliato aver letto i seguenti riferimenti:

• l’appendice Appendice F;
• il capitolo Random Variables and Probability Distributions in Chan & Kroese (2025);
• il capitolo Random variables and their distributions in Blitzstein & Hwang (2019);
  
• il capitolo Random Variables and Distributions in Schervish & DeGroot (2014).

AttenzionePreparazione del Notebook

here::here("code", "_common.R") |> 
  source()

6.1 Definizione di variabile casuale

Nel linguaggio del calcolo delle probabilità, una variabile casuale rappresenta un ponte formale tra il mondo degli eventi qualitativi e quello dell’analisi numerica. Essa formalizza l’idea di assegnare un valore numerico a ciascun possibile risultato di un esperimento aleatorio, trasformando così esiti anche non numerici — come il seme di una carta da gioco o l’esito di un test medico — in quantità misurabili. Questa traduzione in valori numerici è fondamentale per applicare gli strumenti propri della teoria della probabilità e dell’analisi statistica allo studio dei fenomeni aleatori.

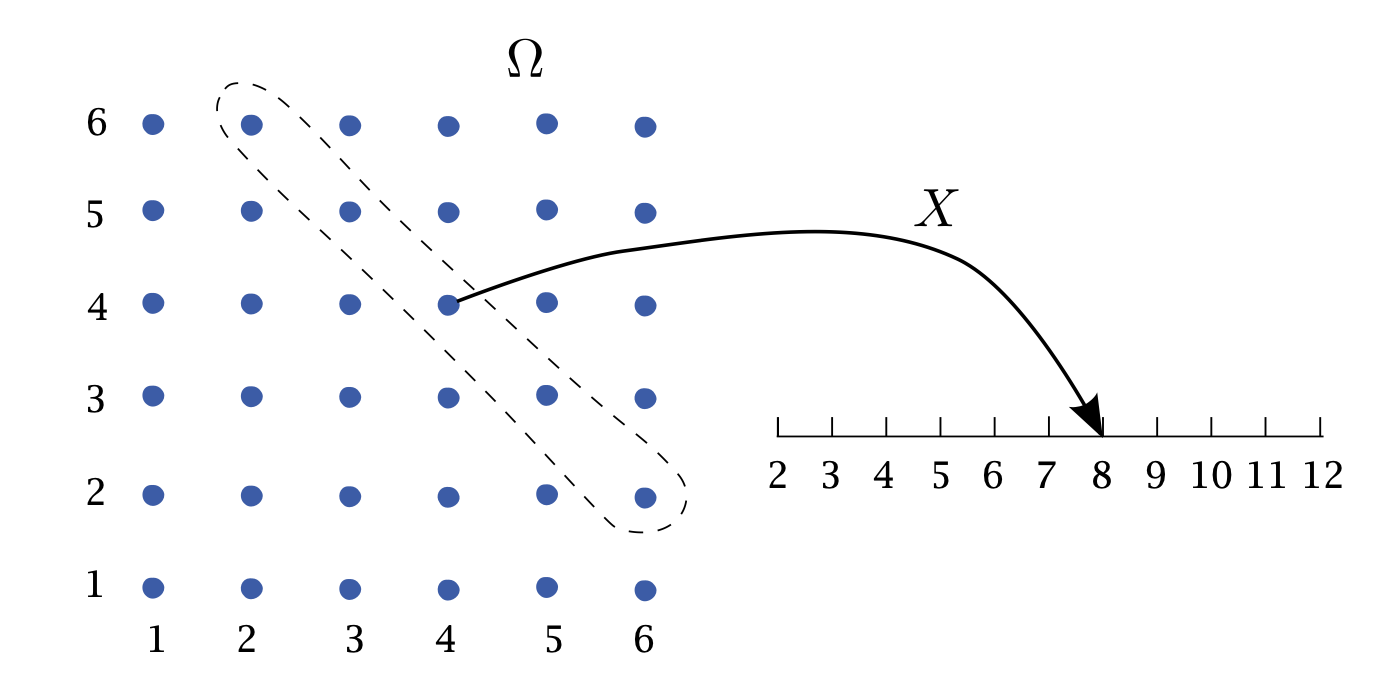
In termini formali, sia \(\Omega\) uno spazio campionario, ovvero l’insieme di tutti i possibili risultati di un esperimento. Una variabile casuale \(X\) è una funzione
\[ X : \Omega \longrightarrow \mathbb{R} \] che assegna a ogni elemento \(\omega \in \Omega\) un unico numero reale \(X(\omega)\).

Ad esempio, nel lancio di una moneta, dove \(\Omega = \{T, C\}\), potremmo definire una variabile casuale \(X\) tale che \(X(T) = 1\) e \(X(C) = 0\). In questo modo, un esito qualitativo viene codificato numericamente, permettendo di calcolare proprietà come il valore atteso o la varianza, e facilitando operazioni altrimenti complesse o impossibili su oggetti non numerici.

Grazie a questa definizione, è possibile modellare matematicamente il comportamento aleatorio e analizzare attraverso un quadro analitico coerente fenomeni probabilistici anche molto diversi tra loro.

NotaEsempio

Lanciamo due dadi equilibrati e annotiamo la somma dei valori delle loro facce. Ogni lancio genera una coppia di valori \((i,j)\), dove \(i\) è il risultato del primo dado e \(j\) il risultato del secondo dado. Lo spazio campionario completo dei possibili esiti è:

\[ \Omega = \{(1,1), (1,2), \dots, (6,5), (6,6)\}. \]

Definiamo una variabile casuale \(X\) che associa ciascun esito \((i,j)\) alla somma dei valori ottenuti dai due dadi, cioè:

\[ X(i,j) = i + j. \]

Ad esempio, se il primo dado mostra 4 e il secondo dado mostra 4, allora l’esito è \((4,4)\) e la variabile casuale \(X\) assume il valore 8.

La variabile aleatoria \(X\) rappresenta la somma di due dadi (figura tratta da Chan & Kroese, 2025).

Consideriamo il valore specifico \(X=8\): questo valore può essere ottenuto attraverso cinque diversi esiti dello spazio campionario: \((2,6), (3,5), (4,4), (5,3), (6,2)\). Indichiamo con \(\{X=8\}\) l’insieme di questi esiti. Poiché tutti gli esiti in \(\Omega\) sono equiprobabili, possiamo calcolare la probabilità di ottenere una somma pari a 8 come:

\[ P(X=8) = \frac{5}{36}. \]

6.2 Tipologie di variabili casuali

Le variabili casuali si dividono in due categorie principali:

6.2.1 Variabili casuali discrete

Una variabile casuale discreta assume un insieme finito o numerabile di valori. Gli esempi includono il numero di teste ottenute in lanci di moneta o la somma dei risultati di due dadi. Per queste variabili, la funzione di massa di probabilità (PMF) assegna a ciascun valore \(x\) la probabilità \(P(X = x)\).

Esempio 6.1 Nel lancio di due dadi, la variabile \(X\) (somma dei punti) può assumere valori interi da 2 a 12. La distribuzione di \(X\) si ottiene contando i casi favorevoli per ciascun valore e dividendo per il numero totale di esiti (36).

6.2.2 Variabili casuali continue

Una variabile casuale continua può assumere infiniti valori in un intervallo (ad esempio, l’altezza di una persona). In questo caso non si assegna una probabilità a un singolo valore (che risulterebbe essere zero), ma si definisce una funzione di densità di probabilità (PDF), tale che l’integrale della funzione su un intervallo fornisce la probabilità che la variabile cada in quell’intervallo.

Esempio 6.2 Considera una variabile \(X\) che rappresenta l’altezza in centimetri. Invece di \(P(X = 170)\), calcoliamo probabilità come \(P(170 \leq X \leq 180)\) mediante l’integrale della PDF in quell’intervallo.

6.3 Notazione convenzionale

Nella teoria della probabilità si adotta una convenzione chiara per distinguere una variabile casuale dal suo valore osservato o realizzato:

• la variabile casuale viene indicata con lettere maiuscole (es. \(X\));
• il valore specifico assunto dalla variabile casuale viene indicato con lettere minuscole (es. \(x\)).

Questa convenzione aiuta a evitare ambiguità, soprattutto quando si definiscono:

• probabilità cumulative: \(P(X \leq x)\);
• valore atteso: \(E[X]\);
• funzioni di densità o massa di probabilità: \(f_X(x)\).

6.4 Variabili casuali multiple

In molti esperimenti, è utile considerare contemporaneamente più variabili casuali. Ad esempio, supponiamo di lanciare una moneta equilibrata tre volte. Definiamo tre variabili casuali indipendenti \(X_1\), \(X_2\) e \(X_3\), ciascuna associata all’esito di un lancio:

\[ P(X_n = 1) = 0.5 \quad (\text{testa}), \qquad P(X_n = 0) = 0.5 \quad (\text{croce}), \quad n = 1, 2, 3. \] Possiamo poi definire una nuova variabile casuale derivata, ad esempio:

\[ Z = X_1 + X_2 + X_3, \] che rappresenta il numero totale di teste ottenute nei tre lanci. In questo scenario, \(Z\) è una variabile casuale discreta che può assumere esclusivamente i valori 0, 1, 2 o 3.

6.5 Distribuzione di probabilità

Definizione 6.1 La distribuzione di probabilità di una variabile casuale descrive come le probabilità sono assegnate ai possibili valori (o intervalli di valori) della variabile.

6.5.1 Funzione di massa di probabilità (PMF) per variabili discrete

Per una variabile casuale discreta \(X\), la distribuzione è definita tramite la funzione di massa di probabilità (PMF), indicata con \(f(x)\), dove:

\[ f(x) = P(X = x). \]

Nota la PMF, è possibile calcolare la probabilità di qualsiasi evento associato a \(X\). Ad esempio, per un insieme \(B\) di valori:

\[ P(X \in B) = \sum_{x \in B} f(x). \]

NotaEsempio

Consideriamo nuovamente il lancio di due dadi, definendo \(X\) come la somma dei loro valori. La tabella seguente mostra chiaramente tutti i casi possibili, il numero di combinazioni per ogni somma, e la relativa probabilità:

\(X\)	Casi Favorevoli	Numero di Casi	\(P(X = x)\)
2	\((1,1)\)	1	\(\frac{1}{36}\)
3	\((1,2), (2,1)\)	2	\(\frac{2}{36} = \frac{1}{18}\)
4	\((1,3), (2,2), (3,1)\)	3	\(\frac{3}{36} = \frac{1}{12}\)
5	\((1,4), (2,3), (3,2), (4,1)\)	4	\(\frac{4}{36} = \frac{1}{9}\)
6	\((1,5), (2,4), (3,3), (4,2), (5,1)\)	5	\(\frac{5}{36}\)
7	\((1,6), (2,5), (3,4), (4,3), (5,2), (6,1)\)	6	\(\frac{6}{36} = \frac{1}{6}\)
8	\((2,6), (3,5), (4,4), (5,3), (6,2)\)	5	\(\frac{5}{36}\)
9	\((3,6), (4,5), (5,4), (6,3)\)	4	\(\frac{4}{36} = \frac{1}{9}\)
10	\((4,6), (5,5), (6,4)\)	3	\(\frac{3}{36} = \frac{1}{12}\)
11	\((5,6), (6,5)\)	2	\(\frac{2}{36} = \frac{1}{18}\)
12	\((6,6)\)	1	\(\frac{1}{36}\)

Per esempio, la probabilità di ottenere una somma pari a 7 è \(\frac{1}{6}\) perché ci sono 6 combinazioni favorevoli su 36 possibili.

6.5.2 Funzione di distribuzione cumulativa (CDF)

Definizione 6.2 La funzione di distribuzione cumulativa (CDF) di una variabile casuale \(X\) è definita come: \[ F(x) = P(X \leq x). \] La CDF indica la probabilità che \(X\) assuma valori minori o uguali a un valore specifico \(x\).

6.5.3 Proprietà della CDF (funzione di ripartizione)

La CDF descrive la probabilità che una variabile casuale \(X\) assuma un valore minore o uguale a \(x\). Per capirla in psicologia (ad esempio, per analizzare dati di test, questionari, o esperimenti), bastano tre idee chiave:

1. Non diminuisce mai:
   Se consideriamo valori \(x\) sempre più grandi, la probabilità cumulata non può diminuire.
   • Esempio: Se la CDF a \(x = 50\) in un test è \(0.7\), a \(x = 60\) sarà almeno \(0.7\) (potrebbe salire, ma non scendere).
     
   • Perché? Aggiungendo nuovi risultati (es.: punteggi più alti), la probabilità totale può solo aumentare o restare uguale.
2. Estremi prevedibili:
   • Per valori molto bassi (es.: \(x \to -\infty\)), la probabilità cumulata è 0: non esistono punteggi infinitamente bassi.
     
   • Per valori molto alti (es.: \(x \to +\infty\)), la probabilità cumulata è 1: tutti i possibili risultati sono inclusi.
     
   • Esempio: In una scala Likert da 1 a 5, la CDF a \(x = 0\) è 0, e a \(x = 10\) è 1.
3. Niente salti “a sorpresa” verso destra:
   La CDF è costruita in modo che, se ci spostiamo di pochissimo a destra di un punto \(x\), la probabilità cumulata non crolla improvvisamente.
   • Esempio:
     Supponiamo che in un questionario, il punteggio \(x = 10\) corrisponda a una certa probabilità cumulata (es.: \(0.8\)). Se ci spostiamo di un millesimo a destra (es.: \(x = 10.001\)), la probabilità rimane \(0.8\), a meno che \(10.001\) non sia un punteggio valido.
     
   • A cosa serve? Garantisce coerenza: se un punteggio \(x\) ha una certa probabilità, questa non viene “persa” spostandosi di poco a destra.

6.5.4 CDF per variabili discrete

In psicologia, spesso lavoriamo con dati discreti (es.: risposte a item di un test, come “1 = Mai” a “5 = Sempre”). In questi casi:

• La CDF si calcola sommando le probabilità di tutti i valori \(\leq x\).
  
• Esempio: Se in una scala da 1 a 5, il 30% degli studenti risponde 1 o 2, allora \(F(2) = 0.3\).
  
• Graficamente: La CDF avrà “gradini” nei punti corrispondenti ai valori possibili (es.: 1, 2, 3, 4, 5).

6.5.4.1 Perché serve saperlo?

Queste proprietà aiutano a:

1. Interpretare grafici cumulativi (es.: quanto è probabile che un partecipante abbia un punteggio \(\leq\) 20?).
   
2. Evitare errori logici (es.: non ha senso aspettarsi un calo della probabilità cumulata all’aumentare di \(x\)).
   
3. Leggere correttamente salti nei dati discreti (es.: un gradino in \(x = 4\) indica un accumulo di probabilità in quel punto).

NotaEsempio

Riprendendo l’esempio della variabile casuale \(X\) definita come la somma di due dadi, possiamo riassumere PMF e CDF in una tabella unica:

\(x\)	\(P(X = x)\)	\(F(x)\)
2	\(\frac{1}{36}\)	\(\frac{1}{36}\)
3	\(\frac{2}{36}\)	\(\frac{3}{36}\)
4	\(\frac{3}{36}\)	\(\frac{6}{36}\)
5	\(\frac{4}{36}\)	\(\frac{10}{36}\)
6	\(\frac{5}{36}\)	\(\frac{15}{36}\)
7	\(\frac{6}{36}\)	\(\frac{21}{36}\)
8	\(\frac{5}{36}\)	\(\frac{26}{36}\)
9	\(\frac{4}{36}\)	\(\frac{30}{36}\)
10	\(\frac{3}{36}\)	\(\frac{33}{36}\)
11	\(\frac{2}{36}\)	\(\frac{35}{36}\)
12	\(\frac{1}{36}\)	\(1\)

6.5.5 Simulazione della distribuzione di probabilità

Spesso, anche se è possibile calcolare analiticamente la distribuzione di probabilità (come nel caso dei due dadi), può essere utile ottenere una stima empirica attraverso la simulazione. Questo approccio prevede di ripetere l’esperimento molte volte e di analizzare le frequenze relative dei risultati ottenuti.

NotaEsempio

Simulazione del lancio di due dadi in R.

1. Simulare il lancio di un singolo dado

# Funzione per simulare un dado a sei facce
lancia_dado <- function() {
  sample(1:6, 1)
}

2. Simulare il lancio di due dadi

# Funzione per simulare il lancio di due dadi ripetuto n volte
lancia_due_dadi <- function(n) {
  risultati <- numeric(n)
  
  for (i in 1:n) {
    risultati[i] <- lancia_dado() + lancia_dado()
  }
  
  risultati
}

3. Eseguire la simulazione

# Numero totale di simulazioni
numero_lanci <- 100000

# Simulazione dei lanci
risultati_simulazione <- lancia_due_dadi(numero_lanci)

# Visualizza i primi 20 risultati
cat("Primi 20 risultati:", risultati_simulazione[1:20], "\n")
#> Primi 20 risultati: 5 5 4 5 5 8 5 8 6 12 7 7 6 9 7 7 11 10 7 6

4. Calcolare e visualizzare la distribuzione empirica

# Calcola la frequenza assoluta per ciascuna somma
frequenze_assolute <- table(risultati_simulazione)
frequenze_assolute
#> risultati_simulazione
#>     2     3     4     5     6     7     8     9    10    11    12 
#>  2919  5489  8216 11140 13909 16884 13931 11059  8248  5408  2797

# Calcola direttamente le frequenze relative (probabilità empiriche)
probabilita_empiriche <- frequenze_assolute / numero_lanci
probabilita_empiriche
#> risultati_simulazione
#>      2      3      4      5      6      7      8      9     10     11     12 
#> 0.0292 0.0549 0.0822 0.1114 0.1391 0.1688 0.1393 0.1106 0.0825 0.0541 0.0280

# Crea una tabella finale chiara e semplice
distribuzione_empirica <- data.frame(
  Somma = as.numeric(names(probabilita_empiriche)),
  Probabilita = as.vector(probabilita_empiriche)
)

# Mostra la distribuzione empirica
print(distribuzione_empirica)
#>    Somma Probabilita
#> 1      2      0.0292
#> 2      3      0.0549
#> 3      4      0.0822
#> 4      5      0.1114
#> 5      6      0.1391
#> 6      7      0.1688
#> 7      8      0.1393
#> 8      9      0.1106
#> 9     10      0.0825
#> 10    11      0.0541
#> 11    12      0.0280

Chiarimento sintetico dei concetti chiave.

• Cos’è una simulazione?
  È un esperimento realizzato al computer che replica più volte un evento casuale per osservare i possibili risultati e la loro frequenza.

• Distribuzione empirica
  È la frequenza con cui ogni risultato (in questo caso, la somma di due dadi) appare nella simulazione. Con più simulazioni, questa distribuzione si avvicina sempre di più a quella prevista dalla teoria.

• Probabilità teorica ed empirica
  La probabilità teorica è calcolata matematicamente: ad esempio, la somma “7” è teoricamente più frequente perché ci sono più modi di ottenerla (6+1, 5+2, 4+3, ecc.).
  La probabilità empirica, invece, si ottiene dalla simulazione pratica, ed è una buona approssimazione della probabilità teorica quando il numero di prove è grande.

6.6 Distribuzioni per variabili continue

Definizione 6.3 Una variabile casuale continua è una variabile aleatoria \(X\) caratterizzata da una distribuzione di probabilità continua. Formalmente, \(X\) si definisce continua se soddisfa le seguenti proprietà:

1. Esistenza della funzione di densità (pdf):
   Esiste una funzione non negativa \(f(x)\), detta funzione di densità di probabilità (pdf, dall’inglese probability density function), tale che:

   • \(f(x) \geq 0\) per ogni \(x \in \mathbb{R}\);
     
   • L’area totale sotto la curva di \(f(x)\) è pari a 1:
     \[ \int_{-\infty}^{+\infty} f(x) \, dx = 1. \]

2. Calcolo delle probabilità tramite integrazione:
   Per ogni intervallo \((a, b] \subseteq \mathbb{R}\) (con \(a < b\)), la probabilità che \(X\) assuma valori in \((a, b]\) è data dall’integrale della pdf su tale intervallo:

   \[ P(a < X \leq b) = \int_{a}^{b} f(x) \, dx. \]

   Questa probabilità coincide anche con la differenza della funzione di ripartizione (CDF, cumulative distribution function) \(F(x) = P(X \leq x)\) agli estremi dell’intervallo:

   \[ P(a < X \leq b) = F(b) - F(a). \]

6.6.1 Proprietà chiave delle variabili continue

• Probabilità in un punto nulla:
  A differenza delle variabili discrete, per una variabile continua la probabilità di assumere un valore esatto \(x_0\) è sempre zero:

  \[ P(X = x_0) = 0. \]

  Questo avviene perché la probabilità è legata all’area sotto la curva \(f(x)\), e un singolo punto ha “larghezza zero”, risultando in un’area nulla. Di conseguenza, per variabili continue:

  \[ P(a \leq X \leq b) = P(a < X \leq b) = P(a \leq X < b) = P(a < X < b). \]

• Interpretazione della densità:
  La funzione \(f(x)\) non rappresenta direttamente una probabilità, ma descrive come la probabilità si distribuisce nello spazio campionario. Valori maggiori di \(f(x)\) indicano regioni in cui è più probabile che \(X\) assuma valori (densità di probabilità).

• Modellizzazione di fenomeni continui:
  Le distribuzioni continue sono utilizzate per rappresentare grandezze misurabili con precisione arbitraria, come tempo, lunghezze, o temperature. Esempi comuni includono la distribuzione normale, esponenziale e uniforme continua.

Riflessioni conclusive

In questo capitolo abbiamo introdotto e approfondito il concetto fondamentale di variabile casuale, illustrando come questo strumento permetta di formalizzare e analizzare matematicamente fenomeni casuali complessi. Attraverso esempi intuitivi, come il lancio di dadi o la simulazione di situazioni reali, abbiamo osservato come le variabili casuali consentano di tradurre domande astratte in analisi concrete e interpretabili.

Abbiamo esaminato le due principali tipologie di variabili casuali—discrete e continue—e discusso le relative distribuzioni di probabilità. Le distribuzioni discrete, caratterizzate da una funzione di massa di probabilità (PMF), si prestano particolarmente bene a modellare situazioni in cui gli eventi possono essere enumerati (come punteggi in test psicologici o risultati di giochi). Al contrario, le distribuzioni continue, descritte dalla funzione di densità di probabilità (PDF), sono essenziali per modellare misure precise, come l’altezza o il tempo, dove il numero di possibili valori è teoricamente infinito.

Un aspetto importante trattato è la funzione di distribuzione cumulativa (CDF), che fornisce una descrizione completa della distribuzione di una variabile casuale, facilitando la comprensione intuitiva della probabilità che un evento accada entro certi limiti. Conoscere le proprietà della CDF aiuta a prevenire errori comuni nella sua interpretazione e a trarre conclusioni più affidabili dai dati empirici.

Infine, attraverso l’utilizzo della simulazione, abbiamo mostrato come sia possibile avvicinarsi empiricamente a una distribuzione teorica, confermando e visualizzando in modo pratico e immediato concetti astratti. Questa capacità di simulare e verificare empiricamente le distribuzioni è estremamente utile, soprattutto quando i modelli teorici diventano troppo complessi da risolvere analiticamente.

Nei prossimi capitoli approfondiremo ulteriormente questi concetti, esaminando alcune distribuzioni di probabilità specifiche che sono comunemente usate nella ricerca psicologica e nelle applicazioni pratiche. Questo ci permetterà di passare da una conoscenza teorica delle variabili casuali a una competenza concreta nel loro utilizzo e nella loro interpretazione, sviluppando strumenti che miglioreranno le nostre capacità di analisi e di decisione in ambito psicologico e statistico.

ImportanteProblemi 1

Consiglio gli esercizi di base disponibili nella seguente pagina web.

ImportanteProblemi 2

Esercizi sulla distribuzione normale, risolvibili usando R, sono disponibili sulla seguente pagina web.

NotaInformazioni sull’ambiente di sviluppo

sessionInfo()
#> R version 4.5.1 (2025-06-13)
#> Platform: aarch64-apple-darwin20
#> Running under: macOS Tahoe 26.0
#> 
#> Matrix products: default
#> BLAS:   /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRblas.0.dylib 
#> LAPACK: /Library/Frameworks/R.framework/Versions/4.5-arm64/Resources/lib/libRlapack.dylib;  LAPACK version 3.12.1
#> 
#> locale:
#> [1] C.UTF-8/UTF-8/C.UTF-8/C/C.UTF-8/C.UTF-8
#> 
#> time zone: Europe/Rome
#> tzcode source: internal
#> 
#> attached base packages:
#> [1] stats     graphics  grDevices utils     datasets  methods   base     
#> 
#> other attached packages:
#>  [1] pillar_1.11.1         tinytable_0.13.0      patchwork_1.3.2      
#>  [4] ggdist_3.3.3          tidybayes_3.0.7       bayesplot_1.14.0     
#>  [7] ggplot2_4.0.0         reliabilitydiag_0.2.1 priorsense_1.1.1     
#> [10] posterior_1.6.1       loo_2.8.0             rstan_2.32.7         
#> [13] StanHeaders_2.32.10   brms_2.23.0           Rcpp_1.1.0           
#> [16] sessioninfo_1.2.3     conflicted_1.2.0      janitor_2.2.1        
#> [19] matrixStats_1.5.0     modelr_0.1.11         tibble_3.3.0         
#> [22] dplyr_1.1.4           tidyr_1.3.1           rio_1.2.3            
#> [25] here_1.0.2           
#> 
#> loaded via a namespace (and not attached):
#>  [1] svUnit_1.0.8          tidyselect_1.2.1      farver_2.1.2         
#>  [4] S7_0.2.0              fastmap_1.2.0         TH.data_1.1-4        
#>  [7] tensorA_0.36.2.1      digest_0.6.37         timechange_0.3.0     
#> [10] estimability_1.5.1    lifecycle_1.0.4       survival_3.8-3       
#> [13] magrittr_2.0.4        compiler_4.5.1        rlang_1.1.6          
#> [16] tools_4.5.1           knitr_1.50            bridgesampling_1.1-2 
#> [19] htmlwidgets_1.6.4     curl_7.0.0            pkgbuild_1.4.8       
#> [22] RColorBrewer_1.1-3    abind_1.4-8           multcomp_1.4-28      
#> [25] withr_3.0.2           purrr_1.1.0           grid_4.5.1           
#> [28] stats4_4.5.1          colorspace_2.1-1      xtable_1.8-4         
#> [31] inline_0.3.21         emmeans_1.11.2-8      scales_1.4.0         
#> [34] MASS_7.3-65           cli_3.6.5             mvtnorm_1.3-3        
#> [37] rmarkdown_2.29        ragg_1.5.0            generics_0.1.4       
#> [40] RcppParallel_5.1.11-1 cachem_1.1.0          stringr_1.5.2        
#> [43] splines_4.5.1         parallel_4.5.1        vctrs_0.6.5          
#> [46] V8_7.0.0              Matrix_1.7-4          sandwich_3.1-1       
#> [49] jsonlite_2.0.0        arrayhelpers_1.1-0    systemfonts_1.2.3    
#> [52] glue_1.8.0            codetools_0.2-20      distributional_0.5.0 
#> [55] lubridate_1.9.4       stringi_1.8.7         gtable_0.3.6         
#> [58] QuickJSR_1.8.0        htmltools_0.5.8.1     Brobdingnag_1.2-9    
#> [61] R6_2.6.1              textshaping_1.0.3     rprojroot_2.1.1      
#> [64] evaluate_1.0.5        lattice_0.22-7        backports_1.5.0      
#> [67] memoise_2.0.1         broom_1.0.10          snakecase_0.11.1     
#> [70] rstantools_2.5.0      gridExtra_2.3         coda_0.19-4.1        
#> [73] nlme_3.1-168          checkmate_2.3.3       xfun_0.53            
#> [76] zoo_1.8-14            pkgconfig_2.0.3

Bibliografia

Blitzstein, J. K., & Hwang, J. (2019). Introduction to probability. CRC Press.

Chan, J. C. C., & Kroese, D. P. (2025). Statistical Modeling and Computation (2ª ed.). Springer.

Schervish, M. J., & DeGroot, M. H. (2014). Probability and statistics (Vol. 563). Pearson Education London, UK: