here::here("code", "_common.R") |>
source()
# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(ggplot2, dplyr, tidyr, patchwork)5 Il teorema di Bayes
“It is, without exaggeration, perhaps the most important single equation in history.”
– Tom Chivers (2024)
Introduzione
Il teorema di Bayes rappresenta il culmine naturale del framework bayesiano che abbiamo costruito progressivamente nei capitoli precedenti. Tale sviluppo concettuale si basa su solide fondamenta: la concezione della probabilità come grado di credenza razionale in uno stato di informazione (Capitolo 1), la comprensione degli assiomi come vincoli di coerenza tra credenze (Capitolo 2), il riconoscimento dell’equiprobabilità come caso speciale derivante dalla simmetria epistemica (Capitolo 3) e l’identificazione della probabilità condizionata come meccanismo fondamentale di aggiornamento delle credenze (Capitolo 4).
Il teorema di Bayes emerge direttamente dalla definizione di probabilità condizionata e fornisce la soluzione formale al problema fondamentale dell’inferenza induttiva: come aggiornare razionalmente le credenze riguardanti ipotesi o cause non direttamente osservabili alla luce di evidenze empiriche osservate.
In questo capitolo esploreremo il teorema non solo come formula tecnica, ma anche come principio di razionalità epistemica, ovvero il modo ottimale per combinare in modo sistematico la conoscenza pregressa (distribuzione a priori) con le nuove osservazioni (funzione di verosimiglianza) e ottenere credenze aggiornate e coerenti (distribuzione a posteriori). Esamineremo applicazioni concrete in ambito diagnostico-clinico, nella ricerca psicologica sperimentale e nel ragionamento quotidiano in condizioni di incertezza.
Panoramica del capitolo
- Derivazione del teorema di Bayes dalla probabilità condizionata.
- Interpretazione epistemica dei componenti (prior, likelihood, posterior).
- Forma in odds e likelihood ratio per applicazioni cliniche.
- Probabilità inversa: il problema fondamentale dell’inferenza.
- Applicazioni a test diagnostici e decisioni cliniche.
- Fallacia del tasso base e fallacia del procuratore.
- Visualizzazioni con distribuzioni Beta.
- Collegamenti al flusso di lavoro bayesiano completo.
5.1 Derivazione del teorema di Bayes
Il teorema di Bayes non costituisce un principio nuovo o indipendente, ma emerge come una conseguenza algebrica diretta della definizione di probabilità condizionata.
5.1.1 La simmetria fondamentale della probabilità congiunta
Come abbiamo visto nel Capitolo 4, la probabilità congiunta di due eventi ammette due rappresentazioni equivalenti:
\[ P(A \cap B) = P(A \mid B) \cdot P(B) = P(B \mid A) \cdot P(A). \tag{5.1}\]
Questa simmetria fondamentale discende immediatamente dall’applicazione della definizione di probabilità condizionata in entrambe le direzioni. Uguagliando le due espressioni e risolvendo per \(P(A \mid B)\) si ottiene la formulazione canonica del teorema:
Teorema 5.1 (Teorema di Bayes (forma fondamentale)) Per eventi \(A\) e \(B\) con \(P(B) > 0\):
\[ P(A \mid B) = \frac{P(B \mid A) \cdot P(A)}{P(B)}. \tag{5.2}\]
Componenti epistemiche:
- distribuzione a priori: \(P(A)\) — rappresenta la credenza iniziale in \(A\) prima dell’osservazione di \(B\);
- funzione di verosimiglianza: \(P(B \mid A)\) — quantifica quanto l’evidenza \(B\) è attesa nell’ipotesi che \(A\) sia vero;
- evidenza marginale: \(P(B)\) — costituisce la probabilità complessiva di osservare \(B\) e funge da costante di normalizzazione;
- distribuzione a posteriori: \(P(A \mid B)\) — esprime la credenza rivista in \(A\) dopo aver osservato \(B\).
Forma proporzionale (spesso più intuitiva nelle applicazioni): \[ P(A \mid B) \propto P(B \mid A) \cdot P(A). \]
La distribuzione a posteriori risulta proporzionale al prodotto della verosimiglianza per la distribuzione a priori; la costante di normalizzazione \(P(B)\) garantisce che le probabilità risultanti rispettino l’assioma di normalizzazione.
5.1.2 Collegamento alle tabelle di probabilità congiunta
Il teorema di Bayes risulta geometricamente evidente quando esaminato attraverso la lente delle tabelle di probabilità congiunta introdotte nel Capitolo 2:
| \(B\) | \(B^c\) | Marginali | |
|---|---|---|---|
| \(A\) | \(P(A \cap B)\) | \(P(A \cap B^c)\) | \(P(A)\) |
| \(A^c\) | \(P(A^c \cap B)\) | \(P(A^c \cap B^c)\) | \(P(A^c)\) |
| Marginali | \(P(B)\) | \(P(B^c)\) | \(1\) |
In questa rappresentazione tabellare, i componenti del teorema di Bayes assumono un’interpretazione geometrica immediata:
- distribuzione a priori: \(P(A)\) corrisponde alla probabilità marginale della riga associata ad \(A\);
- funzione di verosimiglianza: \(P(B \mid A) = P(A \cap B) / P(A)\) rappresenta il rapporto tra la cella congiunta e la marginale di riga;
- distribuzione a posteriori: \(P(A \mid B) = P(A \cap B) / P(B)\) costituisce il rapporto tra la cella congiunta e la marginale di colonna.
Interpretazione geometrica: il teorema di Bayes descrive formalmente come “ruotare” la prospettiva probabilistica da una condizionata all’altra sfruttando la struttura simmetrica della distribuzione congiunta. Questa rotazione epistemica permette di convertire la probabilità dell’evidenza dato lo stato (\(P(B \mid A)\)) nella probabilità dello stato dato l’evidenza (\(P(A \mid B)\)) attraverso la mediazione delle probabilità marginali.
# Esempio numerico con tabella congiunta
# Depressione (D) e Test positivo (T+)
P_D <- 0.15
sens <- 0.85
fp_rate <- 0.10
# Costruire tabella (come in Cap. 2)
P_D_and_Tpos <- sens * P_D
P_D_and_Tneg <- (1 - sens) * P_D
P_Dc_and_Tpos <- fp_rate * (1 - P_D)
P_Dc_and_Tneg <- (1 - fp_rate) * (1 - P_D)
tab <- matrix(
c(P_D_and_Tpos, P_D_and_Tneg, P_Dc_and_Tpos, P_Dc_and_Tneg),
nrow = 2, byrow = TRUE,
dimnames = list(Stato = c("D", "D^c"), Test = c("T+", "T-"))
)
cat("Tabella congiunta:\n")
#> Tabella congiunta:
print(round(tab, 4))
#> Test
#> Stato T+ T-
#> D 0.128 0.0225
#> D^c 0.085 0.7650# Calcolare via Bayes
P_B <- sum(tab[, 1]) # P(T+) = marginale colonna
P_A_given_B <- tab[1, 1] / P_B # P(D | T+)#>
#> === TEOREMA DI BAYES DALLA TABELLA ===
#> Prior: P(D) = 0.15
#> Likelihood: P(T+ | D) = 0.85
#> Evidence: P(T+) = 0.212
#> Posterior: P(D | T+) = 0.6
#> Verifica formula:
#> (sens × P(D)) / P(T+) = 0.6 ✓5.2 Interpretazione epistemica: il meccanismo di aggiornamento
Il teorema di Bayes formalizza il ragionamento induttivo razionale. Vediamo come opera.
5.2.1 I tre ingredienti
Prior \(P(H)\): rappresenta la nostra credenza iniziale nell’ipotesi \(H\) prima dell’osservazione dei dati. Questa valutazione preliminare si basa su diverse fonti di informazione, come le conoscenze pregresse derivanti da studi precedenti, l’esperienza clinica consolidata, le stime di prevalenza o i tassi di base nella popolazione rilevante, o, in condizioni di massima ignoranza, l’applicazione del principio di indifferenza.
Likelihood \(P(E \mid H)\): quantifica quanto l’evidenza osservata \(E\) sia compatibile con l’ipotesi \(H\); È cruciale distinguere questa quantità da \(P(H \mid E)\), confusione frequente nota come “fallacia della probabilità inversa”. La funzione di verosimiglianza rappresenta la capacità predittiva dell’ipotesi e, nei contesti diagnostici, corrisponde ai concetti di sensibilità e specificità dei test.
Posterior \(P(H \mid E)\): esprime la credenza rivista nell’ipotesi \(H\) dopo l’osservazione dell’evidenza \(E\). Questa quantità integra coerentemente la distribuzione a priori con la funzione di verosimiglianza tramite il meccanismo bayesiano. Essa fornisce la risposta formalmente corretta alla domanda inferenziale di interesse pratico e, nei processi sequenziali di apprendimento, funge da nuova distribuzione a priori per gli aggiornamenti successivi basati su nuove evidenze.
5.2.2 Il processo di aggiornamento
#> AGGIORNAMENTO BAYESIANO:
#> ┌─────────────┐
#> │ PRIOR │ P(H) = Conoscenza pregressa
#> │ P(H) │
#> └──────┬──────┘
#> │
#> │ × (moltiplica)
#> │
#> ┌──────▼──────┐
#> │ LIKELIHOOD │ P(E|H) = Compatibilità dati con H
#> │ P(E|H) │
#> └──────┬──────┘
#> │
#> │ ÷ (normalizza)
#> │
#> ┌──────▼──────┐
#> │ EVIDENCE │ P(E) = Prob marginale dei dati
#> │ P(E) │
#> └──────┬──────┘
#> │
#> ▼
#> ┌─────────────┐
#> │ POSTERIOR │ P(H|E) = Credenza aggiornata
#> │ P(H|E) │
#> └─────────────┘5.2.3 Formulazione con partizione dello spazio delle ipotesi
Nelle applicazioni pratiche, la probabilità marginale dell’evidenza \(P(E)\) risulta spesso non direttamente disponibile. Tuttavia, è possibile calcolarla ricorrendo alla legge della probabilità totale (discussa nel Capitolo 4), che consente di scomporre \(P(E)\) rispetto a una partizione dello spazio delle ipotesi:
\[ P(E) = P(E \mid H) P(H) + P(E \mid H^c) P(H^c). \tag{5.3}\]
Sostituendo questa espressione nel teorema di Bayes si ottiene la formulazione estesa:
\[ P(H \mid E) = \frac{P(E \mid H) \cdot P(H)}{P(E \mid H) P(H) + P(E \mid H^c) P(H^c)}. \tag{5.4}\]
Questa rappresentazione è particolarmente utile nei contesti diagnostici e decisionali, in cui le probabilità condizionate \(P(E \mid H)\) e \(P(E \mid H^c)\)—corrispondenti rispettivamente alla sensibilità e al tasso di falsi positivi—sono solitamente note grazie alla validazione degli strumenti di misurazione.
5.3 Forma in odds e likelihood ratio
Per le applicazioni in ambito clinico e diagnostico, la formulazione del teorema di Bayes in termini di odds risulta spesso più intuitiva e operativamente vantaggiosa.
Definizione 5.1 (Teorema di Bayes in forma odds) Gli odds rappresentano il rapporto tra la probabilità di un’ipotesi e la probabilità della sua alternativa: \[ \text{Odds}(H) = \frac{P(H)}{P(H^c)} = \frac{P(H)}{1 - P(H)}. \]
Il teorema di Bayes assume quindi la seguente forma moltiplicativa: \[ \underbrace{\text{Odds}(H \mid E)}_{\text{Posterior odds}} = \underbrace{\text{Odds}(H)}_{\text{Prior odds}} \times \underbrace{\frac{P(E \mid H)}{P(E \mid H^c)}}_{\text{Likelihood Ratio (LR)}}. \tag{5.5}\]
Vantaggi della forma odds.
L’approccio basato sugli odds presenta diversi vantaggi operativi. L’aggiornamento bayesiano si riduce a una semplice operazione di moltiplicazione degli odds a priori per il likelihood ratio associato all’evidenza osservata. Il likelihood ratio possiede un’interpretabilità diretta come quantificazione della forza discriminatoria dell’evidenza a favore o contro l’ipotesi. Evidenze statisticamente indipendenti possono essere combinate in modo moltiplicativo attraverso il prodotto dei rispettivi likelihood ratio, semplificando notevolmente l’integrazione di informazioni provenienti da fonti multiple.
5.3.1 Likelihood ratio nella diagnostica psicologica
Nel contesto dei test diagnostici, il likelihood ratio assume forme specifiche che collegano direttamente le proprietà psicometriche dello strumento alla sua utilità clinica:
-
LR+ (likelihood ratio positivo): \(\frac{\text{Sensibilità}}{1 - \text{Specificità}}\).
- Quantifica quanto un risultato positivo al test è più probabile nei soggetti con la condizione clinica rispetto a quelli senza.
-
LR- (likelihood ratio negativo): \(\frac{1 - \text{Sensibilità}}{\text{Specificità}}\).
- Quantifica quanto un risultato negativo al test è più probabile nei soggetti con la condizione clinica rispetto a quelli senza.
Interpretazione clinica del likelihood ratio:
- valori di \(\text{LR} > 1\) indicano evidenza a favore della presenza della condizione;
- valori di \(\text{LR} < 1\) indicano evidenza a favore dell’assenza della condizione;
- valori di \(\text{LR} = 1\) indicano che il test non fornisce informazione discriminatoria.
Classificazione pratica della forza dell’evidenza (approssimativa):
- \(\text{LR} > 10\) o \(< 0.1\): evidenza forte a favore o contro la condizione;
- \(\text{LR}\) compreso tra 5-10 o 0.1-0.2: evidenza moderata;
- \(\text{LR}\) compreso tra 2-5 o 0.2-0.5: evidenza debole ma suggestiva.
# Esempio: calcolare LR per test diagnostico
sens <- 0.85
spec <- 0.90
LR_pos <- sens / (1 - spec)
LR_neg <- (1 - sens) / spec#> === LIKELIHOOD RATIOS ===
#> Test con sensibilità = 0.85 e specificità = 0.9
#> LR+ = 8.5
#> Interpretazione: Un test positivo è 8.5 volte più probabile nei depressi vs non depressi
#> LR- = 0.17
#> Interpretazione: Un test negativo è 0.17 volte più probabile nei depressi vs non depressi
#> (quindi molto meno probabile, evidenza contro depressione)5.3.2 Nomogramma di Fagan
Il nomogramma di Fagan è uno strumento grafico che permette di applicare visivamente il teorema di Bayes in forma odds, particolarmente utile nei contesti clinici in cui è necessario un ragionamento diagnostico rapido ma rigoroso.
Il principio fondamentale su cui si basa il nomogramma è la proprietà additiva delle trasformazioni logaritmiche: in scala log-odds, l’aggiornamento bayesiano si riduce a una semplice addizione.
# Funzioni di conversione
prob_to_odds <- function(p) p / (1 - p)
odds_to_prob <- function(o) o / (1 + o)
logit <- function(p) log(p / (1 - p))
inv_logit <- function(x) 1 / (1 + exp(-x))
# Esempio: prior 15%, LR+ = 8.5
prior_prob <- 0.15
prior_odds <- prob_to_odds(prior_prob)
# Aggiornamento con test positivo
post_odds_pos <- prior_odds * LR_pos
post_prob_pos <- odds_to_prob(post_odds_pos)
# Aggiornamento con test negativo
post_odds_neg <- prior_odds * LR_neg
post_prob_neg <- odds_to_prob(post_odds_neg)#>
#> === AGGIORNAMENTO IN FORMA ODDS ===
#> Prior:
#> P(D) = 0.15
#> Odds(D) = 0.176
#> Dopo test POSITIVO (LR+ = 8.5 ):
#> Odds(D|T+) = 0.176 × 8.5 = 1.5
#> P(D|T+) = 0.6
#> Dopo test NEGATIVO (LR- = 0.167 ):
#> Odds(D|T-) = 0.176 × 0.167 = 0.029
#> P(D|T-) = 0.0286# Visualizzazione tipo nomogramma
df_nomogram <- data.frame(
Step = factor(c("Prior", "LR+", "Posterior+", "Prior", "LR-", "Posterior-"),
levels = c("Prior", "LR+", "Posterior+", "LR-", "Posterior-")),
LogOdds = c(logit(prior_prob), log(LR_pos), logit(post_prob_pos),
logit(prior_prob), log(LR_neg), logit(post_prob_neg)),
Branch = c("Positivo", "Positivo", "Positivo", "Negativo", "Negativo", "Negativo")
)
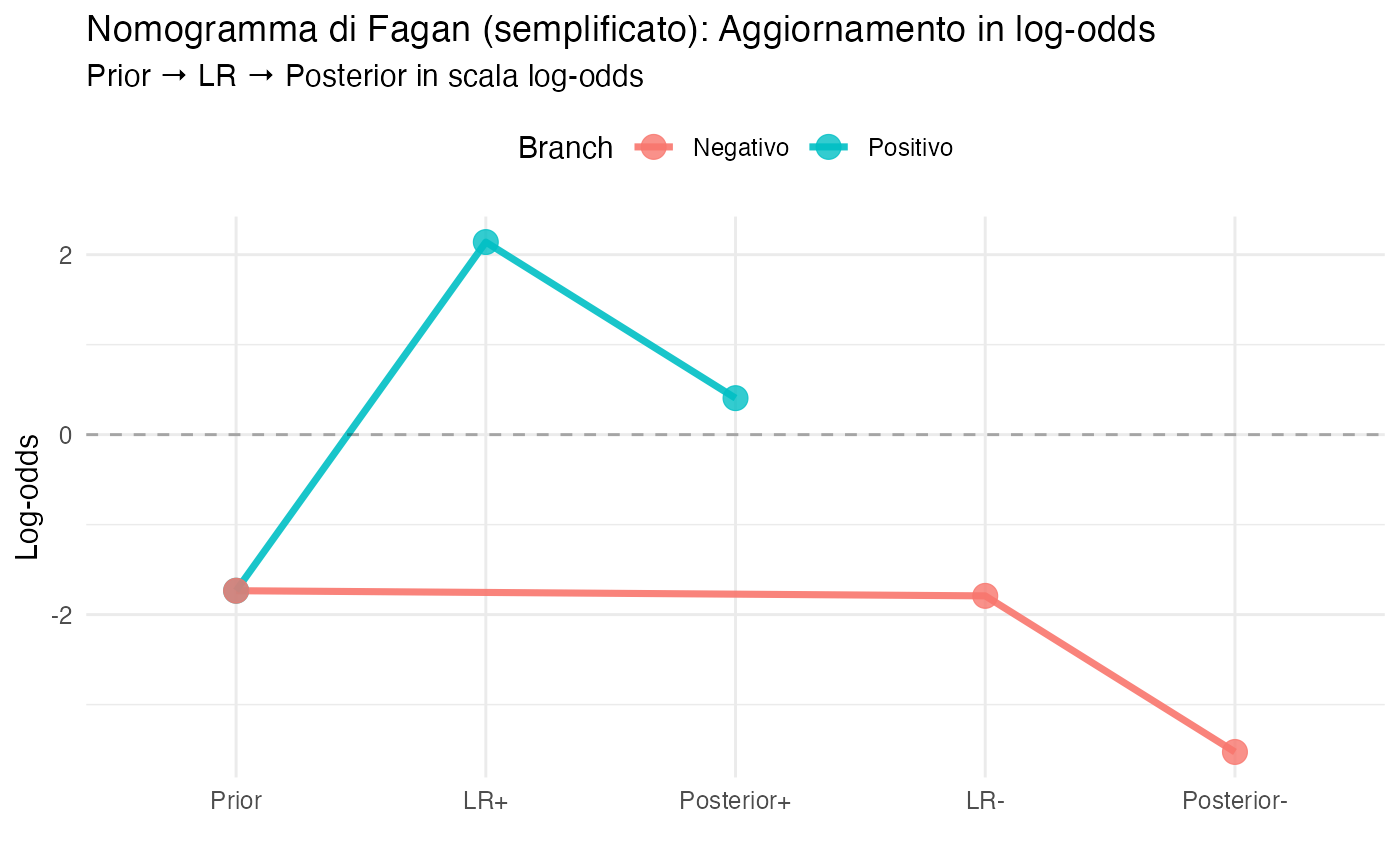
Interpretazione del nomogramma: il grafico visualizza il processo di aggiornamento bayesiano in tre fasi. La linea orizzontale tratteggiata a zero rappresenta l’equiprobabilità (odds = 1, probabilità = 0.5). Il ramo superiore mostra come un test positivo (LR+ > 1) sposti verso l’alto le credenze, aumentando la probabilità della condizione. Il ramo inferiore mostra come un test negativo (LR- < 1) sposti verso il basso le credenze, riducendo la probabilità della condizione. In scala log-odds, queste traslazioni corrispondono esattamente ai logaritmi dei rispettivi rapporti di verosimiglianza.
5.4 Probabilità inversa: il cuore dell’inferenza bayesiana
Il teorema di Bayes fornisce la soluzione al problema fondamentale dell’inferenza scientifica e clinica: l’inversione della direzione del condizionamento probabilistico.
5.4.1 La sfida inferenziale
Nella ricerca scientifica e nella pratica clinica, le informazioni disponibili riguardano tipicamente:
- \(P(\text{Dati} \mid \text{Ipotesi})\) — la probabilità di osservare determinati dati nell’ipotesi che una teoria sia vera.
Tuttavia, la domanda di reale interesse è:
- \(P(\text{Ipotesi} \mid \text{Dati})\) — il grado di credibilità dell’ipotesi alla luce dei dati effettivamente osservati.
La confusione tra queste due quantità probabilistiche costituisce un errore inferenziale grave e purtroppo diffuso.
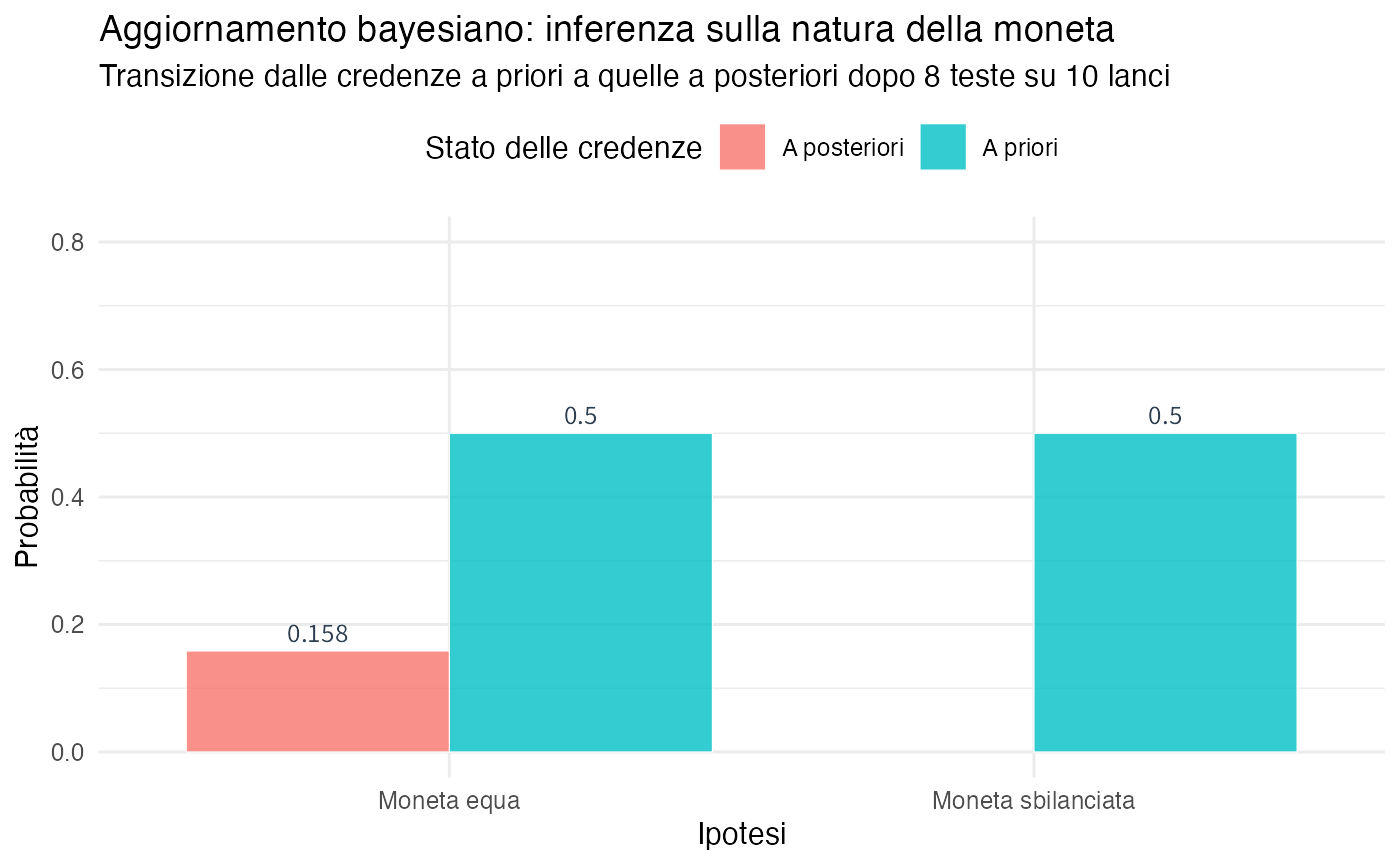
5.4.2 Esempio: inferenza su moneta potenzialmente sbilanciata
NotaInferenza bayesiana su parametro ignoto
Moneta sospetta
Scenario sperimentale: Si eseguono 10 lanci di una moneta ottenendo 8 risultati “testa”. La questione inferenziale riguarda la natura della moneta: è equa (\(\theta = 0.5\)) oppure presenta uno sbilanciamento a favore di testa (\(\theta = 0.7\))?
Approccio frequentista (con limitazioni evidenti): - Calcola \(P(\text{8 teste} \mid \theta = 0.5) = \binom{10}{8} (0.5)^{10} \approx 0.044\) - Conclude: “L’ipotesi di equità è statisticamente significativa al livello 0.05” - Tuttavia, questo approccio non fornisce informazioni su quanto credere nell’ipotesi alternativa di sbilanciamento
Approccio bayesiano (inferenza completa):
# Specificazione dei dati sperimentali
n <- 10
k <- 8
# Definizione delle ipotesi in esame
theta_fair <- 0.5
theta_biased <- 0.7
# Distribuzione a priori (assumiamo equiprobabilità iniziale tra le ipotesi)
prior_fair <- 0.5
prior_biased <- 0.5
# Calcolo delle funzioni di verosimiglianza
lik_fair <- dbinom(k, n, theta_fair)
lik_biased <- dbinom(k, n, theta_biased)
# Aggiornamento bayesiano
evidence <- lik_fair * prior_fair + lik_biased * prior_biased
post_fair <- (lik_fair * prior_fair) / evidence
post_biased <- (lik_biased * prior_biased) / evidence#> ANALISI BAYESIANA: MONETA EQUA VERSUS SBILANCIATA
#> =================================================
#> DATI SPERIMENTALI: 8 risultati 'testa' su 10 lanci
#> DISTRIBUZIONE A PRIORI:
#> P(Moneta equa) = 0.5
#> P(Moneta sbilanciata) = 0.5
#> FUNZIONI DI VEROSIMIGLIANZA:
#> P(8 teste | Moneta equa) = 0.0439
#> P(8 teste | Moneta sbilanciata) = 0.234
#> RAPPORTO DI VEROSIMIGLIANZA:
#> LR = P(dati|Sbilanciata) / P(dati|Equa) = 5.31
#> Interpretazione: I dati osservati sono 5.31 volte più probabili nell'ipotesi di moneta sbilanciata
#> DISTRIBUZIONE A POSTERIORI:
#> P(Moneta equa | 8 teste) = 0.158
#> P(Moneta sbilanciata | 8 teste) = 0.842
#> CONCLUSIONE INFERENZIALE: I dati forniscono un supporto moderato all'ipotesi
#> di sbilanciamento, ma permane un'incertezza sostanziale riguardo alla vera
#> natura della moneta. Ulteriori osservazioni potrebbero ridurre questa incertezza.Visualizzazione dell’aggiornamento delle credenze:
5.5 Visualizzazioni con distribuzioni Beta
Per parametri continui come le probabilità, le distribuzioni di probabilità forniscono lo strumento naturale per rappresentare in modo completo le nostre credenze epistemiche.
5.5.1 Prior, Likelihood e Posterior nel modello Beta-Binomiale
La distribuzione Beta costituisce la scelta naturale per esprimere credenze riguardanti probabilità \(\theta \in [0,1]\). In combinazione con dati di tipo binomiale, il processo di aggiornamento bayesiano assume una forma particolarmente elegante e computazionalmente efficiente.
# Esempio: Test a scelta multipla con 4 opzioni
# Distribuzione a priori centrata sull'ipotesi di risposta casuale (1/4)
alpha0 <- 1
beta0 <- 3 # Valore atteso = 1/(1+3) = 0.25
# Dati osservati: 12 risposte corrette su 30 tentativi
n <- 30
k <- 12
# Distribuzione a posteriori
alpha1 <- alpha0 + k
beta1 <- beta0 + (n - k)
# Griglia per la visualizzazione
theta <- seq(0, 1, length.out = 500)
# Funzioni di densità
prior_dens <- dbeta(theta, alpha0, beta0)
posterior_dens <- dbeta(theta, alpha1, beta1)
# Funzione di verosimiglianza (proporzionale, normalizzata per visualizzazione)
likelihood_dens <- dbeta(theta, k + 1, n - k + 1) # Proporzionale alla Binomiale
likelihood_dens <- likelihood_dens / max(likelihood_dens) * max(posterior_dens)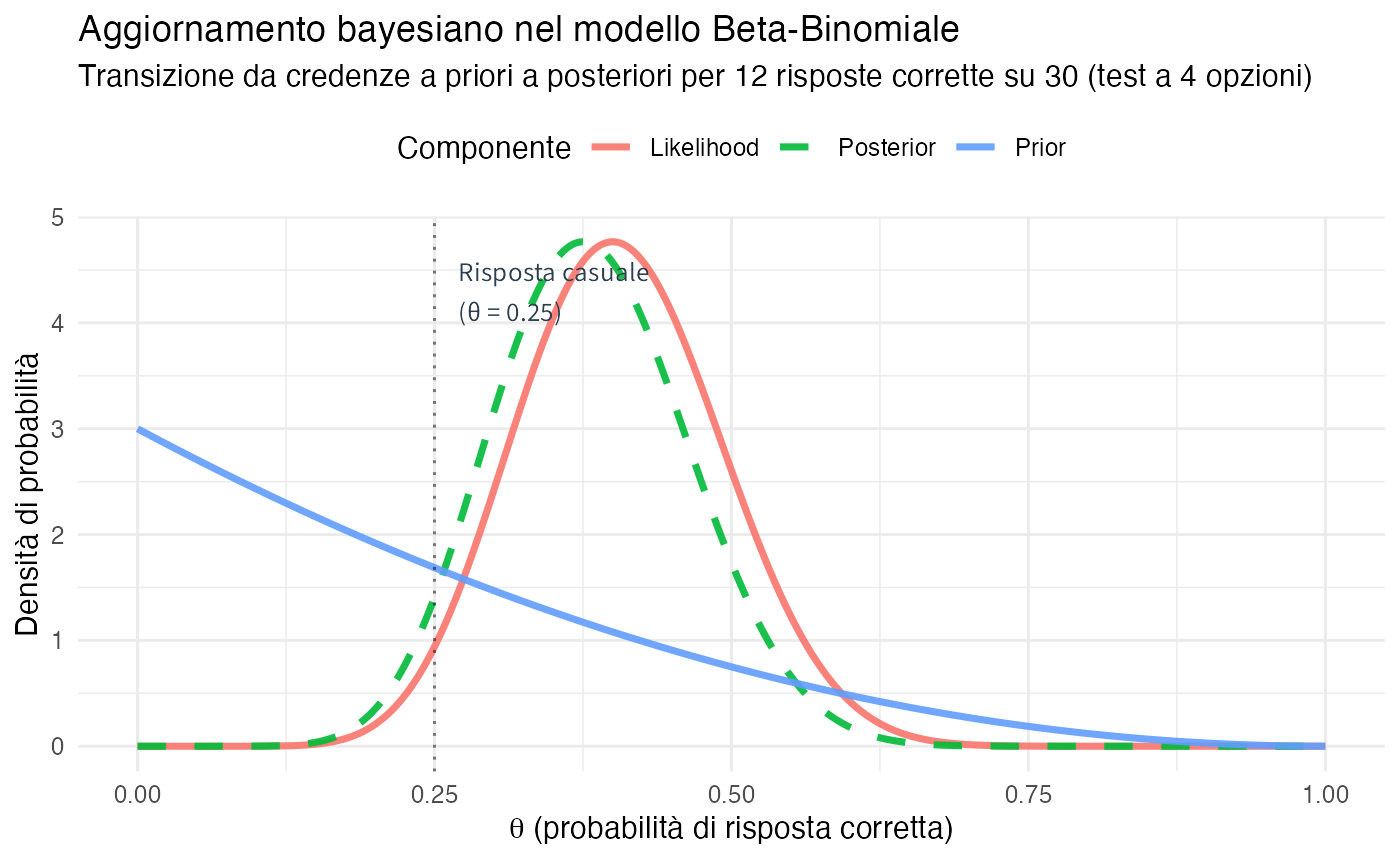
Interpretazione del processo di aggiornamento.
- Distribuzione a priori (rosso): rappresenta le credenze iniziali centrate attorno a 0.25, corrispondente all’ipotesi di risposta puramente casuale.
- Funzione di verosimiglianza (verde tratteggiato): mostra la compatibilità dei dati osservati (12/30 = 0.40) con diversi valori del parametro \(\theta\).
- Distribuzione a posteriori (blu): costituisce la sintesi bayesiana che bilancia credenze iniziali ed evidenza empirica, spostata verso 0.40 ma non completamente.
#> CONFRONTO TRA LE STIME DI θ
#> ============================
#> Stima basata sulla distribuzione a priori: 0.25
#> Stima di massima verosimiglianza (MLE): 0.4
#> Stima basata sulla distribuzione a posteriori: 0.382
#> ANALISI: La distribuzione a posteriori rappresenta un compromesso bayesiano tra
#> le credenze iniziali e l'evidenza empirica. Con l'aumentare della dimensione
#> campionaria, la distribuzione a posteriori convergerebbe progressivamente
#> verso la stima di massima verosimiglianza.5.5.2 Intervalli di credibilità bayesiani
A differenza degli intervalli di confidenza nell’approccio frequentista, gli intervalli di credibilità bayesiani ammettono un’interpretazione probabilistica diretta e intuitiva riguardo al parametro di interesse.
#> INTERVALLO DI CREDIBILITÀ BAYESIANO AL 95%
#> ==========================================
#> Intervallo di credibilità: [ 0.229 , 0.549 ]
#> INTERPRETAZIONE EPISTEMICA DIRETTA:
#> Alla luce della distribuzione a posteriori, assegniamo una probabilità del 95%
#> che il vero valore del parametro θ si trovi all'interno di questo intervallo,
#> dato lo specifico insieme di dati osservati e le nostre credenze iniziali.
#> CONTRASTO CON L'APPROCCIO FREQUENTISTA:
#> Questa interpretazione differisce fondamentalmente da quella degli intervalli
#> di confidenza, che si riferiscono alle proprietà a lungo termine di una
#> procedura di stima piuttosto che alla probabilità riguardante il parametro.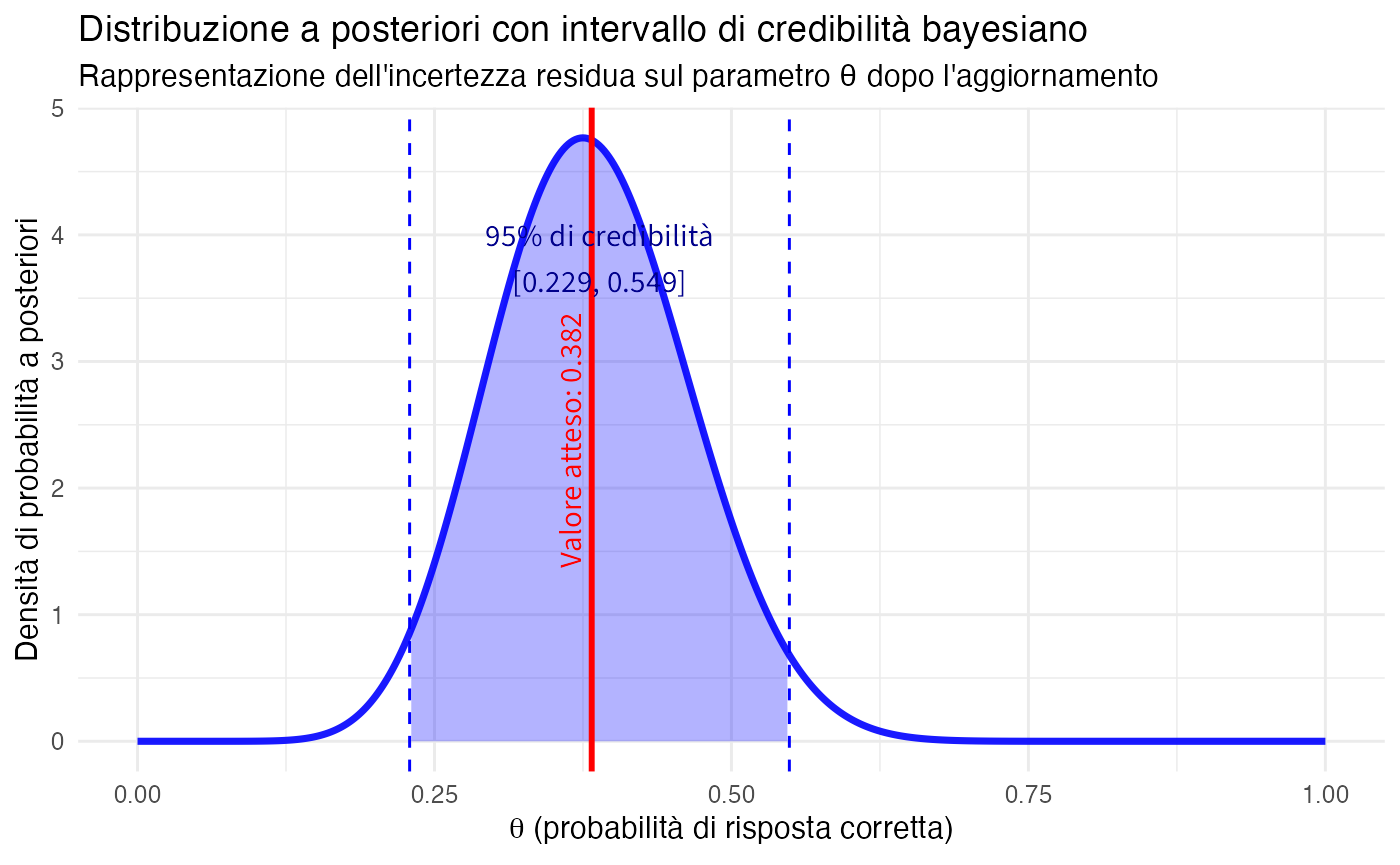
Interpretazione della visualizzazione: l’area ombreggiata in blu rappresenta la regione all’interno della quale assegniamo una probabilità del 95% che si trovi il vero valore del parametro \(\theta\). La linea verticale rossa indica il valore atteso della distribuzione a posteriori, mentre le linee tratteggiate delimitano i confini dell’intervallo di credibilità. Questa rappresentazione fornisce una caratterizzazione completa dell’incertezza residua riguardante il parametro dopo aver considerato sia l’evidenza empirica che le credenze iniziali.
5.6 Applicazioni cliniche e psicologiche del teorema di Bayes
5.6.1 Test diagnostico per il disturbo depressivo maggiore
Riprendiamo l’esempio precedente, ipotizzando una prevalenza della depressione maggiore di circa l’8%, e consideriamo l’utilizzo di un test diagnostico con caratteristiche tecniche validate.
# Prevalenza nella popolazione
P_D <- 0.08 # Prevalenza nella medicina generale
# Caratteristiche del test
sens <- 0.85 # Sensibilità: P(T+|D)
spec <- 0.90 # Specificità: P(T-|sano)
fp_rate <- 1 - spec # Tasso di falsi positivi
# Calcolo delle probabilità posteriori con Bayes
P_Tpos <- sens * P_D + fp_rate * (1 - P_D) # Probabilità totale test positivo
P_D_given_Tpos <- (sens * P_D) / P_Tpos # P(Depresso | Test positivo)
P_Tneg <- (1 - sens) * P_D + spec * (1 - P_D) # Probabilità totale test negativo
P_D_given_Tneg <- ((1 - sens) * P_D) / P_Tneg # P(Depresso | Test negativo)Interpretazione clinica dei risultati:
#> === ANALISI BAYESIANA DEL TEST DIAGNOSTICO ===
#> Contesto: Screening in medicina generale
#> Prevalenza base: 8%
#> CARATTERISTICHE DEL TEST:
#> • Sensibilità (riconosce i veri malati): 85 %
#> • Specificità (riconosce i sani): 90 %
#> • Tasso falsi positivi: 10 %
#> RISULTATI BAYESIANI:
#> • Probabilità pre-test (prior): 8 %
#> • Probabilità post-test positivo (VPP): 42.5 %
#> • Probabilità post-test negativo: 1.43 %
#> INTERPRETAZIONE CLINICA:
#> • Un test POSITIVO aumenta la probabilità da 8% a 42.5 %
#> → Ancora sotto il 50%: molti falsi positivi in popolazioni a bassa prevalenza
#> • Un test NEGATIVO riduce la probabilità a 1.43 %
#> → Test negativo è fortemente rassicurante in questo contesto5.6.2 Fallacia del tasso base
# Analisi sistematica del VPP al variare della prevalenza
prevalences <- seq(0.01, 0.50, by = 0.01)
VPP <- function(prev, sens, spec) {
fp <- 1 - spec
P_Tpos <- sens * prev + fp * (1 - prev)
(sens * prev) / P_Tpos
}
vpps <- VPP(prevalences, sens, spec)
df_baseRate <- data.frame(
Prevalenza = prevalences,
VPP = vpps
)Visualizzazione dell’effetto del tasso base:
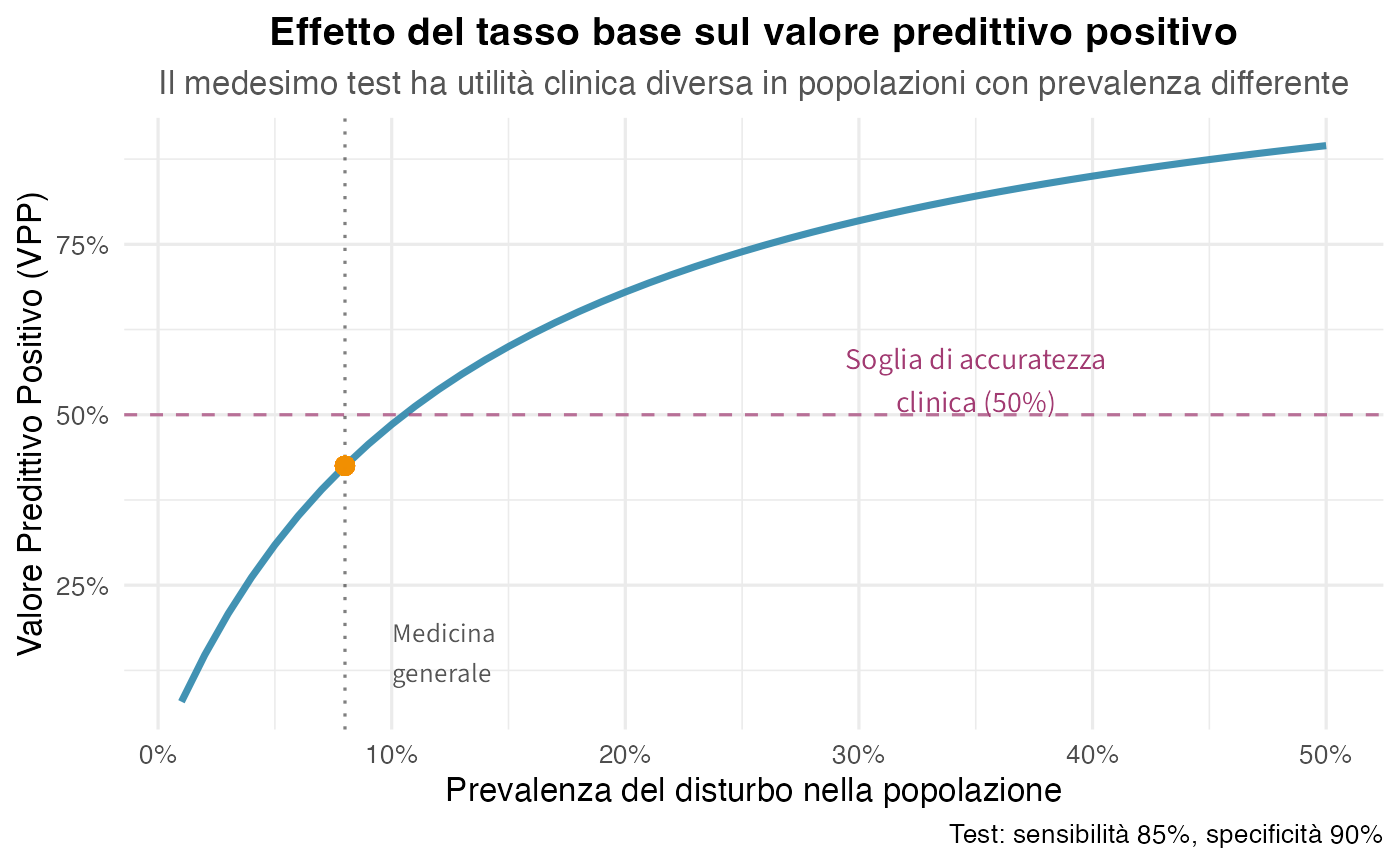
In sintesi: l’utilità di un test dipende criticamente dal contesto. Lo stesso strumento fornisce risultati con affidabilità diversa in popolazioni con prevalenze differenti. Trascurare il tasso di base può alterare l’interpretazione diagnostica, portando a una sovrastima dell’accuratezza dei test positivi in contesti a bassa prevalenza e compromettendo la validità delle conclusioni cliniche.
5.6.3 Test sequenziali: ADHD in età scolare
# Due test indipendenti per ADHD
P_ADHD <- 0.05 # Prevalenza popolazione generale scolare
sens_T1 <- 0.80 # Questionario genitori
spec_T1 <- 0.85
sens_T2 <- 0.75 # Osservazione in classe
spec_T2 <- 0.88
# Calcolare likelihood ratios
LR_pos_T1 <- sens_T1 / (1 - spec_T1)
LR_pos_T2 <- sens_T2 / (1 - spec_T2)
# Aggiornamento sequenziale in odds
prior_odds <- P_ADHD / (1 - P_ADHD)
# Dopo T1+
post_odds_T1 <- prior_odds * LR_pos_T1
post_prob_T1 <- post_odds_T1 / (1 + post_odds_T1)
# Dopo T1+ e T2+ (assumendo indipendenza condizionale)
post_odds_both <- post_odds_T1 * LR_pos_T2
post_prob_both <- post_odds_both / (1 + post_odds_both)#>
#> === DIAGNOSTICA SEQUENZIALE PER ADHD ===
#> Probabilità pre-test: 5% (prevalenza popolazione scolare)
#> DOPO QUESTIONARIO GENITORI (positivo):
#> • Likelihood ratio positivo: 5.33
#> • Probabilità post-test: 0.219
#> • Aumento: da 5% a 21.9 %
#> DOPO OSSERVAZIONE IN CLASSE (positiva):
#> • Likelihood ratio positivo: 6.25
#> • Probabilità finale: 0.637
#> • Aumento cumulativo: da 21.9 % a 63.7 %Visualizzazione della cascata di aggiornamenti:
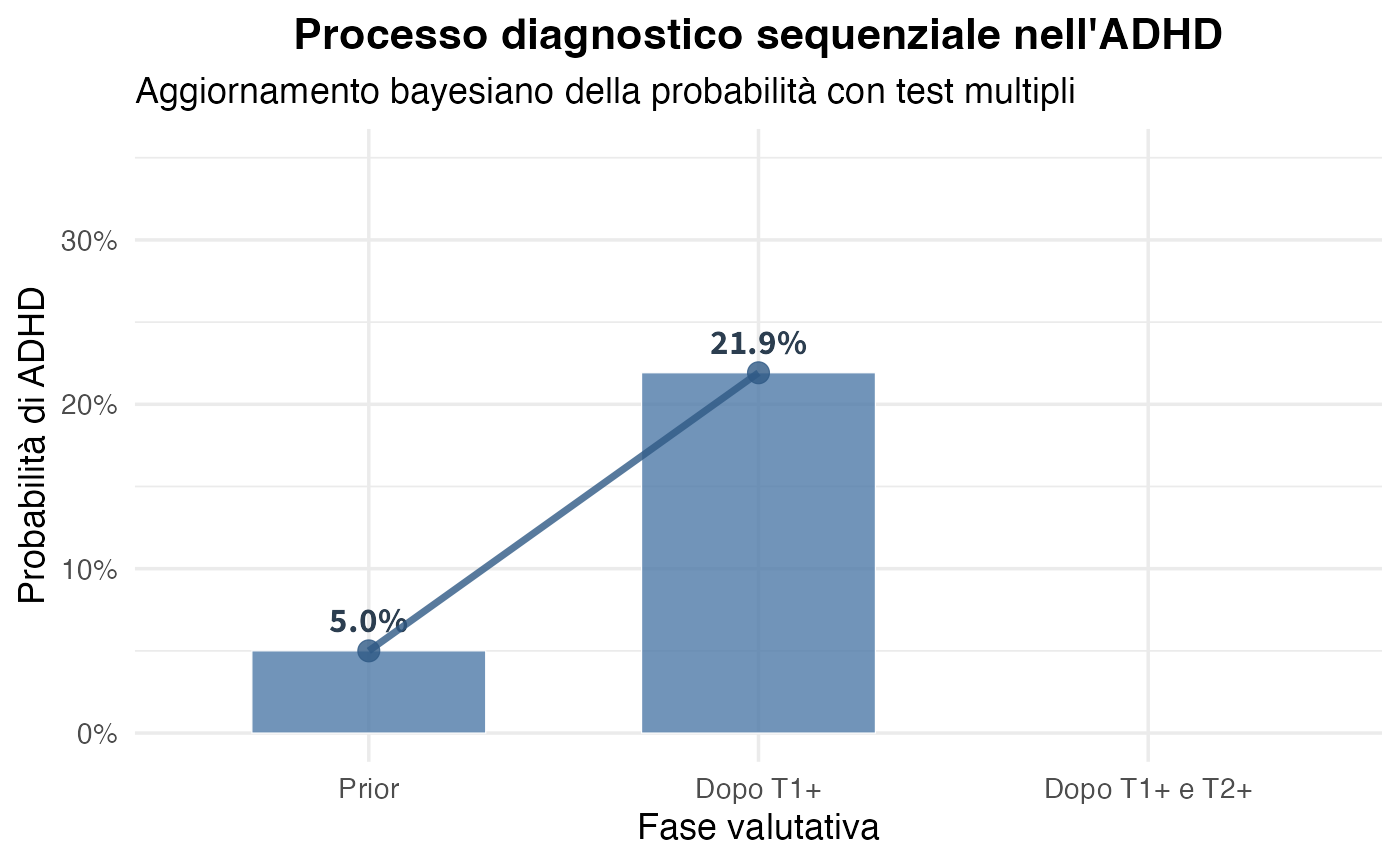
Osservazioni conclusive: questo caso illustra l’applicazione diretta del teorema di Bayes nel processo diagnostico. Ogni test positivo aggiorna iterativamente la probabilità precedente, trasformandola in una nuova probabilità a priori per la valutazione successiva. La probabilità evolve quindi da un iniziale 5% a un 22% dopo il primo test e a un 32% dopo il secondo, dimostrando come l’accumulo di evidenze convergenti incrementi progressivamente la certezza diagnostica. Questo approccio sequenziale formalizza matematicamente il ragionamento clinico e mostra come il teorema di Bayes strutturi il processo decisionale basato sulle prove nella pratica psicologica.
Riflessioni conclusive
Il teorema di Bayes rappresenta il principio fondamentale del ragionamento razionale in condizioni di incertezza e sintetizza e completa il percorso concettuale sviluppato nei capitoli precedenti. Esso deriva naturalmente dalla probabilità condizionata, attraverso la simmetria della distribuzione congiunta, e formalizza il processo di inversione probabilistica che trasforma la probabilità dell’evidenza data un’ipotesi nella probabilità dell’ipotesi data l’evidenza osservata.
Il teorema integra matematicamente in modo ottimale il prior e la likelihood, producendo un posterior che quantifica in modo coerente e trasparente l’aggiornamento delle credenze. Questa struttura si applica naturalmente ai problemi psicologici e clinici, dalla diagnostica alla valutazione della comorbilità fino alle decisioni terapeutiche, dimostrando come il formalismo bayesiano traduca operativamente i processi di ragionamento clinico.
Il percorso attraverso i capitoli ha costruito una progressione concettuale coerente: si è partiti dalla probabilità come grado di credenza razionale, si è passati agli assiomi di coerenza, all’equiprobabilità come caso speciale e al condizionamento come aggiornamento, per poi giungere al teorema di Bayes come sintesi e applicazione di questi principi fondamentali.
Questo capitolo conclude la trattazione dei fondamenti della probabilità bayesiana, aprendo naturalmente a sviluppi più avanzati quali l’inferenza su parametri continui mediante distribuzioni prior e posterior complete, i modelli gerarchici con iperparametri, la selezione di modelli mediante i fattori di Bayes e l’impiego di metodi computazionali sofisticati per problemi complessi. Tuttavia, i principi fondamentali rimangono invariati: la specificazione del prior che incorpora la conoscenza pregressa, la definizione della funzione di verosimiglianza che modella i dati, il calcolo del posterior che aggiorna le credenze e l’inferenza basata sulla distribuzione risultante.
L’approccio bayesiano offre vantaggi distintivi per la ricerca e la pratica in psicologia: fornisce un’interpretabilità diretta attraverso la probabilità delle ipotesi, dati i dati; incorpora esplicitamente la conoscenza esistente dalla letteratura e dall’esperienza clinica; permette inferenze flessibili, non limitate ai test binari; quantifica completamente l’incertezza attraverso distribuzioni, piuttosto che stime puntuali; e supporta naturalmente l’aggiornamento sequenziale, essenziale per la ricerca iterativa e i trial clinici adattivi.
Come osservò Laplace oltre due secoli fa, la probabilità bayesiana rappresenta il buon senso ridotto a calcolo, con il teorema di Bayes che ne costituisce il motore matematico fondamentale, offrendo agli psicologi uno strumento coerente e potente per il ragionamento scientifico e clinico in condizioni di incertezza.
Esercizi
È facile trovare online esercizi sull’applicazione del teorema di Bayes. Consigliamo gli esercizi 1–6 disponibili su questa pagina.
Bibliografia
Chivers, T. (2024). Everything is Predictable: How Bayesian Statistics Explain Our World. Simon; Schuster.