1  Interpretazione bayesiana della probabilità

Introduzione

In questo capitolo esploreremo la probabilità da una prospettiva bayesiana, concependola fin dall’inizio come un grado di credenza razionale piuttosto che come una proprietà fisica degli eventi o una frequenza limite. Questa visione, profondamente radicata nei lavori di Thomas Bayes, Pierre-Simon Laplace e Bruno de Finetti, offre una base concettualmente coerente per affrontare l’incertezza nella ricerca psicologica.

Scopriremo che gli assiomi della probabilità non sono “leggi naturali” della casualità, ma vincoli di coerenza logica tra le nostre credenze. Quando violiamo questi vincoli, le nostre assegnazioni di probabilità diventano contraddittorie e ci espongono a situazioni paradossali (il famoso “Dutch Book”). Le simulazioni al computer, che utilizzeremo ampiamente, non definiranno cosa sia la probabilità, ma illustreranno come credenze coerenti si comportano quando vengono verificate empiricamente.

Panoramica del capitolo

• La probabilità come grado di credenza razionale.
• Incertezza epistemica e ontologica.
• L’argomento della coerenza: Dutch Book e scommesse eque.
• Cenni storici alla tradizione bayesiana.
• Simulazioni come strumento di verifica (non di definizione).

ConsiglioPrerequisiti

• Leggere Why probability probably doesn’t exist (but it is useful to act like it does (Spiegelhalter, 2024).
• Leggere l’Appendice D.

AttenzionePreparazione del Notebook

here::here("code", "_common.R") |> 
  source()

1.1 Casualità e incertezza

La vita è intrinsecamente incerta: non possiamo conoscere con precisione il passato, prevedere il futuro né comprendere appieno la complessità del presente. Come sottolinea David Spiegelhalter, in un recente articolo pubblicato su Nature, questa condizione di ignoranza ci spinge a interpretare la casualità come un modello utile, che pur non offrendo certezze deterministiche, rivela preziose regolarità statistiche (Spiegelhalter, 2024).

Per navigare questa incertezza, è cruciale distinguere tra due concezioni fondamentali della probabilità:

1. Visione ontologica: la probabilità come proprietà intrinseca del mondo fisico (ad esempio, “Questa moneta ha probabilità 0.5 di mostrare testa.”).
2. Visione epistemica: la probabilità come misura della nostra ignoranza e grado di credenza razionale (ad esempio, “In base alle informazioni disponibili, assegno probabilità 0.5 all’uscita di testa.”).

In questo corso adotteremo sistematicamente la prospettiva epistemica, che considera la probabilità non come una caratteristica del mondo, ma come uno strumento per quantificare coerentemente la nostra incertezza alla luce delle informazioni di cui disponiamo.

1.2 Due dimensioni dell’incertezza: epistemica e ontologica

L’incertezza che incontriamo nell’analisi dei fenomeni complessi si manifesta secondo due dimensioni distinte, che riflettono le due visioni della probabilità appena presentate.

1. Incertezza epistemica
   Dipende dai limiti della nostra conoscenza o dai dati a disposizione. Se in un esperimento non si controllano adeguatamente variabili importanti o disponiamo di campioni insufficienti, la nostra valutazione probabilistica risente di queste carenze informative. Questo tipo di incertezza può essere ridotto migliorando il disegno sperimentale, aumentando le osservazioni o acquisendo nuove conoscenze.

2. Incertezza ontologica
   È insita nella natura stessa del fenomeno studiato e persiste indipendentemente dalla precisione delle nostre misurazioni. Il risultato di un lancio di dadi rimane fondamentalmente imprevedibile nel caso singolo, anche disponendo di informazioni dettagliate sulle condizioni iniziali e sulle leggi fisiche coinvolte. Questa casualità è una caratteristica costitutiva del sistema.

Nel framework bayesiano, tuttavia, anche quella che classicamente viene considerata “incertezza ontologica” viene trattata come incertezza epistemica: poiché non abbiamo accesso completo allo stato del sistema, siamo costretti a quantificare la nostra ignoranza attraverso probabilità. Come osservò Laplace, per una mente onnisciente che conoscesse tutte le forze della natura e la posizione di ogni particella, il futuro sarebbe tanto determinato quanto il passato. La probabilità, dunque, non è una proprietà del mondo, ma emerge necessariamente dai limiti della nostra conoscenza.

1.3 Probabilità come grado di credenza

1.3.1 La visione bayesiana soggettivista

Nel paradigma bayesiano, assegnare una probabilità a un evento significa esprimere un grado di fiducia razionale nel verificarsi di quell’evento, basandosi su tutto ciò che si conosce in un dato momento. Questo approccio, sviluppato da Bruno de Finetti, Frank Ramsey e altri pensatori, concepisce la probabilità come fondamentalmente soggettiva, ma non per questo arbitraria.

Probabilità = grado di credenza (plausibilità) assegnato a un’affermazione, in base allo stato dell’informazione.

La definizione si articola attorno a quattro dimensioni fondamentali. La soggettività riconosce che individui diversi, con conoscenze ed esperienze diverse, possono ragionevolmente attribuire probabilità diverse allo stesso evento. Tuttavia, questa soggettività è vincolata dalla razionalità, che impone alle assegnazioni di probabilità di rispettare precisi principi di coerenza logica, come formalizzato negli assiomi della probabilità. Ogni valutazione è inoltre intrinsecamente condizionata dall’insieme di informazioni disponibili al momento della stima. Infine, il quadro è aggiornabile in modo sistematico: quando emergono nuove evidenze, le probabilità possono essere riviste coerentemente tramite il meccanismo dell’aggiornamento bayesiano.

Questa prospettiva trasforma la probabilità da una proprietà oggettiva del mondo a uno strumento logico per quantificare l’incertezza personale alla luce delle conoscenze disponibili.

NotaEsempio: Diagnosi clinica

1.3.2 Probabilità come credenza in psicologia clinica

Consideriamo, ad esempio, l’interpretazione di un test per la depressione. Lo stesso punteggio assume significati clinici profondamente diversi in due contesti diversi:

• se il soggetto è ricoverato in psichiatria, dove la prevalenza del disturbo è elevata;
• se proviene dalla popolazione generale, dove la prevalenza è bassa.

La probabilità che il soggetto sia effettivamente depresso non rappresenta una caratteristica intrinseca del risultato del test, ma piuttosto un grado di credenza razionale che sintetizza diverse fonti di informazione.

Questa valutazione integra sistematicamente:

• le conoscenze pregresse, come la prevalenza del disturbo nel contesto e le informazioni anamnestiche;
• l’evidenza empirica fornita dal test, attraverso i parametri di sensibilità e specificità;
• il ragionamento bayesiano, che combina coerentemente questi elementi.

In questa prospettiva, la probabilità diventa una misura quantitativa della nostra conoscenza incerta sulla condizione del paziente, piuttosto che una proprietà oggettiva e immutabile dell’evento stesso.

1.4 L’argomento della coerenza: Dutch Book

Se la probabilità è soggettiva, come possiamo giustificare gli assiomi matematici che la governano? La risposta viene dall’argomento del Dutch Book, proposto da Bruno de Finetti.

1.4.1 Probabilità come scommessa equa

Bruno de Finetti propose un modo concreto e intuitivo per pensare alla probabilità: immaginala come la tua disposizione personale a scommettere su un evento.

1.4.1.1 Cosa significa nella pratica?

Quando affermi “La probabilità che piova domani è del 70%” \(P(pioggia) = 0.7\), secondo l’interpretazione di De Finetti, stai implicitamente dichiarando che:

considereresti equa la seguente scommessa:

• versi 0.70 euro per acquistare un “biglietto”;
• se domani piove, ricevi 1 euro come vincita;
• se domani non piove, non ricevi nulla.

…saresti quindi indifferente tra accettare o rifiutare questa scommessa. La ritieni perfettamente bilanciata, né a tuo vantaggio né a tuo svantaggio, in linea con la tua valutazione personale delle probabilità.

1.4.1.2 Il linguaggio delle quote e delle scommesse

Nel contesto delle scommesse, la quota rappresenta il prezzo da pagare per acquisire il diritto a una vincita potenziale. Nell’esempio precedente, con una probabilità del 70% di pioggia, una quota di 0.7 indica che si investono 0.70 euro per ogni euro di vincita potenziale.

Se l’evento si verifica (piove), il tuo guadagno netto ammonta a 0.30 euro, ottenuti sottraendo l’investimento iniziale (0.70 €) dalla vincita (1 €). Al contrario, se l’evento non si verifica (non piove), si subisce una perdita totale dell’investimento iniziale di 0.70 euro.

Questa struttura rende evidente come la probabilità soggettiva si traduca, dal punto di vista operativo, in una valutazione economica del rischio.

1.4.1.3 Perché proprio 0.70 è il prezzo equo?

Per comprendere perché 0.70 euro costituisca il prezzo equo in questo contesto, consideriamo cosa accadrebbe se questa stessa scommessa venisse ripetuta numerose volte in condizioni analoghe. Nel 70% dei casi, quando piove effettivamente, si realizza un guadagno netto di 0.30 euro. Nel restante 30% dei casi, caratterizzati dall’assenza di pioggia, si subirebbe una perdita di 0.70 euro. Se estendiamo questo scenario a un numero elevato di replicazioni, guadagni e perdite si compensano a vicenda, confermando l’equità della quota proposta.

Questa intuizione trova una formalizzazione matematica nell’espressione:

Prezzo equo = Probabilità × Vincita + (1 - Probabilità) × Perdita

Applicando la formula al nostro esempio:

Prezzo equo = 0.7 × 1 euro + 0.3 × 0 euro = 0.70 euro

In termini più rigorosi, questa espressione corrisponde al concetto statistico di valore atteso, rappresentabile come:

\[ \text{Prezzo equo} = P(\text{pioggia}) \times 1 + [1 - P(\text{pioggia})] \times 0 = P(\text{pioggia}) \]

Possiamo quindi concludere che la probabilità soggettiva assegnata a un evento coincide con il prezzo massimo che si sarebbe disposti a pagare per ricevere 1 euro in caso di realizzazione dell’evento stesso.

1.4.2 Il Dutch Book: quando le nostre credenze ci portano alla rovina

Immaginate di essere così sicuri delle vostre credenze da essere disposti a scommetterci dei soldi. Cosa succederebbe se queste credenze fossero incoerenti tra loro? Un Dutch Book è proprio questo: una serie di scommesse che, se accettate, garantiscono una perdita matematicamente certa, qualunque cosa accada nella realtà.

Questo concetto ci mostra che gli assiomi della probabilità non sono convenzioni arbitrarie, ma requisiti fondamentali per pensare in modo razionale sull’incertezza.

ImportanteProbabilità coerenti vs incoerenti: un esempio pratico

Scenario 1 – Credenze coerenti: la nostra strategia è a prova di scommessa

Supponiamo di dover prevedere il meteo di domani. Ci sono solo due possibilità mutualmente esclusive:

• A = “Pioverà”;
• B = “Non pioverà”.

Le nostre credenze (espresse come probabilità) sono: \[ P(A) = 0.4, \quad P(B) = 0.6, \quad P(A \cup B) = 1.0. \]

Queste probabilità sono coerenti perché rispettano l’additività: \(0.4 + 0.6 = 1.0\).

Come funzionano le scommesse.

Possiamo pensare alle probabilità come al “prezzo equo” di un biglietto della lotteria. Se \(P(A) = 0.4\), siamo disposti a pagare 0.40 € per un biglietto su \(A\). Se l’evento si verifica, il biglietto paga 1 €; altrimenti, non paga nulla.

• Biglietto su “pioverà”: prezzo 0.40 €, paga 1 € se piove.
• Biglietto su “non pioverà”: prezzo 0.60 €, paga 1 € se non piove.
• Biglietto su “pioverà o non pioverà”: prezzo 1.00 €, paga 1 € (sempre!).

Perché non si può perdere con certezza.

Calcoliamo il valore atteso (quanto ci aspettiamo di guadagnare in media) per ogni biglietto:

\[ \begin{aligned} E[\text{guadagno su A}] &= 0.4 \times 1 - 0.40 = 0 \text{ €}\\ E[\text{guadagno su B}] &= 0.6 \times 1 - 0.60 = 0 \text{ €}\\ E[\text{guadagno su A o B}] &= 1.0 \times 1 - 1.00 = 0 \text{ €} \end{aligned} \]

Risultato: ogni scommessa ha valore atteso zero. Non importa quali biglietti compriamo o vendiamo, o in quale combinazione: in media, nel lungo periodo, non guadagniamo né perdiamo. Nessuno può costruire una strategia che ci garantisca una perdita certa.

Verifica tramite simulazione.

Simuliamo un milione di scenari per verificare empiricamente:

set.seed(123)
n <- 1e6
pA <- 0.4  # Probabilità vera che piova

# Generiamo gli esiti (1 = piove, 2 = non piove)
esito <- ifelse(runif(n) < pA, 1, 2)

# Calcoliamo i profitti per ogni tipo di biglietto
guadagno_A   <- (esito == 1) * 1 - 0.40
guadagno_B   <- (esito == 2) * 1 - 0.60
guadagno_AUB <- 1 - 1.00

# Medie dei guadagni
c(media_A = mean(guadagno_A), 
  media_B = mean(guadagno_B), 
  media_AUB = mean(guadagno_AUB))
#>   media_A   media_B media_AUB 
#>  0.000821 -0.000821  0.000000

Come previsto, tutti i valori oscillano intorno allo zero. Con credenze coerenti siamo al sicuro.

Scenario 2 – Credenze incoerenti: la trappola del Dutch Book

Ora immaginiamo di mantenere le stesse credenze sulla realtà (pioverà davvero con probabilità 0.4), ma di dichiarare credenze personali incoerenti:

\[ P(A) = 0.6, \quad P(B) = 0.5, \quad P(A \cup B) = 0.9. \]

Problema: queste probabilità violano l’additività! Infatti: \(0.6 + 0.5 = 1.1\), ma dichiariamo \(P(A \cup B) = 0.9\). Non può essere che \(A\) e \(B\) insieme abbiano probabilità totale superiore (\(1.1\)) alla loro unione (\(0.9\)).

Come funzionano i biglietti con credenze incoerenti.

Secondo le nostre credenze incoerenti, siamo disposti a:

• Comprare un biglietto su A per 0.60 € (perché pensiamo valga la pena).
• Comprare un biglietto su B per 0.50 € (perché pensiamo valga la pena).
• Vendere un biglietto su A∪B per 0.90 € (perché pensiamo sia un buon prezzo di vendita).

Quando compriamo un biglietto, spendiamo denaro e speriamo che l’evento si verifichi per incassare 1 €. Quando vendiamo un biglietto, incassiamo subito il prezzo, ma ci impegniamo a pagare 1 € se l’evento si verifica.

La strategia vincente dell’avversario contro di noi.

Un avversario astuto nota l’incoerenza e costruisce questo Dutch Book contro di noi:

1. Ci vende il biglietto su “pioverà” a 0.60 € → Noi spendiamo 0.60 €.
2. Ci vende il biglietto su “non pioverà” a 0.50 € → Noi spendiamo 0.50 €.
3. Ci compra il biglietto su “pioverà o non pioverà” a 0.90 € → Noi incassiamo 0.90 €.

Bilancio iniziale per noi: \(-0.60 - 0.50 + 0.90 = -0.20\) €. Abbiamo già perso 0.20 € prima ancora di sapere cosa succederà domani!

Cosa succede in ogni caso possibile.

Vediamo ora cosa accade domani, qualunque sia il meteo:

Caso 1: Piove (evento A)

• Il nostro biglietto su A paga: +1.00 €.
• Il nostro biglietto su B non paga: 0 €.
• Dobbiamo pagare 1 € per il biglietto A∪B che abbiamo venduto: -1.00 €.
• Profitto totale: \(1.00 + 0 - 1.00 - 0.20 = -0.20\) €.

Caso 2: Non piove (evento B)

• Il nostro biglietto su A non paga: 0 €.
• Il nostro biglietto su B paga: +1.00 €.
• Dobbiamo pagare 1 € per il biglietto A∪B che abbiamo venduto: -1.00 €.
• Profitto totale: \(0 + 1.00 - 1.00 - 0.20 = -0.20\) €.

In entrambi i casi perdiamo esattamente 0.20 €. Non c’è scampo: è una perdita matematicamente certa, indipendentemente da cosa succede nella realtà.

Tabella riassuntiva.

Esito	Biglietti che pagano a noi	Biglietti che paghiamo noi	Profitto netto
Piove (A)	1 € (biglietto A)	1 € (biglietto A∪B venduto)	−0.20 €
Non piove (B)	1 € (biglietto B)	1 € (biglietto A∪B venduto)	−0.20 €

Verifica tramite simulazione.

set.seed(123)
n <- 1e6

# Realtà oggettiva
pA_vera <- 0.4  

# I nostri prezzi incoerenti (quanto siamo disposti a pagare/ricevere)
prezzo_A <- 0.60      # Compriamo A
prezzo_B <- 0.50      # Compriamo B
prezzo_AUB <- 0.90    # Vendiamo A∪B

# Flusso di cassa iniziale (abbiamo già perso)
flusso_iniziale <- (-prezzo_A) + (-prezzo_B) + (prezzo_AUB)

# Simulazione degli esiti
esito <- ifelse(runif(n) < pA_vera, 1L, 2L)

# Calcoliamo i payoff finali
payoff_A <- (esito == 1) * 1    # Incassiamo 1€ se piove
payoff_B <- (esito == 2) * 1    # Incassiamo 1€ se non piove
payoff_AUB <- 1                 # Paghiamo sempre 1€ (abbiamo venduto)

# Profitto totale
guadagno_netto <- flusso_iniziale + payoff_A + payoff_B - payoff_AUB

c(guadagno_medio = mean(guadagno_netto),
  guadagno_minimo = min(guadagno_netto), 
  guadagno_massimo = max(guadagno_netto))
#>   guadagno_medio  guadagno_minimo guadagno_massimo 
#>             -0.2             -0.2             -0.2

Risultato: perdiamo esattamente 0.20 € in ogni singola simulazione. Non c’è variabilità, non c’è speranza, non c’è modo di evitarlo.

Lezione fondamentale per la psicologia.

Questo esempio dimostra che:

1. Gli assiomi della probabilità non sono regole astratte, ma requisiti per evitare contraddizioni pratiche nelle nostre decisioni. Se le nostre credenze violano questi assiomi, possiamo essere matematicamente certi di subire perdite.

2. La coerenza delle credenze è misurabile: se le nostre probabilità sono incoerenti, qualcuno può dimostrarlo costruendo un Dutch Book contro di noi—una serie di scommesse che ci fanno perdere con certezza.

3. L’approccio bayesiano ci protegge: assegnare probabilità coerenti (che rispettano gli assiomi) ci garantisce che nessuna strategia possa sfruttare le nostre credenze per assicurarsi un profitto certo a nostre spese.

Quando studiamo come le persone formano giudizi in condizioni di incertezza, il Dutch Book ci ricorda che la razionalità ha requisiti precisi e verificabili. Violare gli assiomi della probabilità non è solo un errore teorico: è una vulnerabilità che, in situazioni reali (mercati finanziari, decisioni mediche, valutazioni forensi), può avere conseguenze concrete e misurabili.

Le persone reali mostrano sistematiche incoerenze nella stima delle probabilità, un fenomeno ampiamente documentato in psicologia. Il concetto di Dutch Book rivela la ricaduta pratica di queste incoerenze: non si tratta di un mero difetto formale, ma di una vulnerabilità decisionale che ci espone a scelte sistematicamente svantaggiose.

1.4.3 Gli assiomi di Kolmogorov come vincoli di coerenza

Gli assiomi di Kolmogorov non sono leggi naturali, ma requisiti minimi per evitare contraddizioni:

1. Non negatività: \(0 \le P(A) \le 1\).
   Un grado di credenza non può essere negativo né superare la certezza assoluta.

2. Normalizzazione: \(P(\Omega) = 1\).
   Siamo certi del fatto che almeno uno degli eventi possibili si verificherà.

3. Additività: Per eventi mutualmente esclusivi \(A \cap B = \varnothing\),
   \[P(A \cup B) = P(A) + P(B).\]

   La fiducia riposta nel verificarsi di \(A\) oppure \(B\) deve corrispondere alla somma delle fiducie assegnate ai due eventi considerati separatamente.

Nel loro insieme, questi principi assicurano che il nostro sistema di credenze sia internamente coerente e ci proteggano dal rischio di strategie di scommessa che garantirebbero perdite certe (Dutch Book).

1.5 Verifica della coerenza con R

Possiamo utilizzare R per verificare sistematicamente la coerenza di un’assegnazione di probabilità.

1.5.1 Esempio 1: verifica di coerenza per eventi mutualmente esclusivi

# Assegnazione di probabilità a eventi mutualmente esclusivi
beliefs <- c(A = 0.6, B = 0.5, C = 0.1)
sum_beliefs <- sum(beliefs)

#> Somma delle probabilità assegnate: 1.2
#> ❌ INCOERENZA: la somma supera 1 per eventi mutualmente esclusivi.
#>    Violazione dell'assioma di additività.
#>    Esposizione al Dutch Book: perdita certa possibile!

1.5.2 Esempio 2: simulazione di scommessa con prezzo equo

Simuliamo una scommessa su un evento \(A\) a cui assegniamo \(P(A) = 0.7\), verificando la coerenza attraverso il valore atteso.

set.seed(123)
p_A <- 0.7
n_bets <- 100000

# Simulazione di esiti coerenti con la probabilità assegnata
A_occurs <- rbinom(n_bets, size = 1, prob = p_A)

# Scommessa con prezzo coerente (pari alla probabilità assegnata)
fair_price <- p_A
payoff_fair <- A_occurs * 1 - fair_price

#> ANALISI PREZZO COERENTE (0.7):
#> Valore atteso del payoff: 0.0009
#> Deviazione standard: 0.458
#> Interpretazione: valore atteso vicino a zero → scommessa equa

Ora testiamo un prezzo incoerente (0.9 per un evento a cui assegniamo probabilità 0.7):

# Scommessa con prezzo incoerente
unfair_price <- 0.9
payoff_unfair <- A_occurs * 1 - unfair_price

#> ANALISI PREZZO INCOERENTE (0.9):
#> Valore atteso del payoff: -0.199
#> Perdita attesa per scommessa: 0.199
#> Interpretazione: valore atteso negativo → sovrapagamento sistematico

Interpretazione dei risultati: se il prezzo della scommessa coincide con la nostra credenza probabilistica (0.7), il valore atteso del payoff è circa zero, il che indica una scommessa equa. Al contrario, un prezzo superiore alla nostra credenza (0.9) genera un valore atteso negativo, indicando che stiamo pagando un prezzo eccessivo per l’evento rispetto alla nostra stessa valutazione della probabilità.

1.6 Cenni storici: la tradizione bayesiana

La teoria della probabilità affonda le sue radici nel XVII secolo con i lavori di Pascal e Fermat sui giochi d’azzardo. Tuttavia, l’interpretazione bayesiana si sviluppò in una tradizione parallela.

1.6.1 Thomas Bayes (1701-1761)

Il reverendo Thomas Bayes sviluppò quello che oggi chiamiamo teorema di Bayes, pubblicato postumo nel 1763. Il suo contributo fondamentale fu quello di riconoscere che è possibile invertire il ragionamento probabilistico: a partire da osservazioni, è possibile aggiornare razionalmente le proprie credenze su cause o parametri non osservati.

1.6.2 Pierre-Simon Laplace (1749-1827)

Laplace sviluppò e generalizzò il lavoro di Bayes applicando l’inferenza probabilistica ai problemi scientifici. La sua concezione della probabilità come “buon senso ridotto a calcolo” anticipò la moderna interpretazione epistemologica.

“La probabilità è relativa in parte all’ignoranza, in parte alla conoscenza.”
– Pierre-Simon Laplace

1.6.3 Bruno de Finetti (1906-1985)

De Finetti gettò le basi della moderna filosofia della probabilità bayesiana soggettivista. La sua famosa affermazione “la probabilità non esiste” significa che la probabilità non è una proprietà del mondo, ma uno strumento per quantificare l’incertezza.

Sviluppò l’argomento del Dutch Book e il concetto di scambiabilità, dimostrando che molti risultati classici (come la legge dei grandi numeri) possono essere derivati senza assumere probabilità “oggettive”.

1.6.4 Harold Jeffreys (1891-1989)

Nel suo influente Theory of Probability (1939), Jeffreys propose un approccio “oggettivo” bayesiano, basato su prior non informativi e principi di invarianza. Dimostrò l’utilità dell’inferenza bayesiana in geofisica e in altre scienze.

1.6.5 La rinascita moderna

Dopo un periodo di eclissi dovuto al dominio della statistica frequentista (Fisher, Neyman-Pearson), l’approccio bayesiano ha conosciuto una rinascita negli anni ’90 grazie:

• alla potenza computazionale (MCMC, Stan, JAGS);
• a nuovi testi divulgativi (Gelman, McElreath, Kruschke);
• all’applicazione in machine learning e AI.

1.7 Il ruolo delle simulazioni: illustrazione, non definizione

Una differenza cruciale rispetto all’approccio classico è il ruolo delle simulazioni e della Legge dei Grandi Numeri (LLN).

1.7.1 L’approccio frequentista classico (e i suoi limiti)

Nella prospettiva frequentista classica, la probabilità di un evento è definita dal suo comportamento asintotico in un numero molto elevato di prove ripetute:

\[ P(A) = \lim_{n \to \infty} \frac{\text{frequenza di occorrenza di A}}{n}. \]

La Legge dei Grandi Numeri garantisce che, in condizioni ideali, le frequenze relative osservate convergano effettivamente verso questo valore limite. Questo approccio implica tre assunzioni fondamentali:

• Oggettività: la probabilità è considerata una proprietà intrinseca del fenomeno, indipendente dall’osservatore;
• Misurabilità: le simulazioni e gli esperimenti servono a “scoprire” o stimare questa probabilità preesistente;
• Definizione operativa: la probabilità è definita attraverso il suo metodo di misurazione (la frequenza limite).

Tuttavia, questa prospettiva presenta diverse criticità quando viene applicata ai contesti decisionali reali:

• risulta problematica per gli eventi non ripetibili (es. “probabilità che domani piova”);
• presuppone l’esistenza di un limite che, nella pratica, non è mai osservabile;
• non fornisce un framework per quantificare l’incertezza in situazioni singole o uniche.

1.7.2 L’approccio bayesiano

Nella prospettiva bayesiana, la probabilità rappresenta un grado di credenza razionale riguardo al verificarsi di un evento, basato sulle informazioni disponibili. Questo approccio si basa su tre principi fondamentali:

• la probabilità come credenza: le assegnazioni probabilistiche esprimono il nostro stato di informazione e incertezza prima di osservare i dati;
• verifica della coerenza: le simulazioni servono a confermare che credenze iniziali coerenti si traducono in comportamenti attesi delle frequenze empiriche;
• convergenza esplicativa: la Legge dei Grandi Numeri spiega perché le frequenze osservate tendono a coincidere con le nostre credenze, ma non definisce cosa sia la probabilità.

In questo framework, la probabilità non è una proprietà da “scoprire” nel mondo, ma uno strumento logico per quantificare sistematicamente l’incertezza e aggiornare coerentemente le nostre convinzioni alla luce di nuove evidenze.

ImportanteDifferenza filosofica fondamentale

Prospettiva frequentista:
“La probabilità è 0.5 perché, lanciando la moneta infinite volte, la frequenza relativa delle teste convergerà al 50%.”

Prospettiva bayesiana:
“Assegno probabilità 0.5 in base al principio di indifferenza, poiché non ho informazioni che mi portino a privilegiare un esito rispetto all’altro. La legge dei grandi numeri mi garantisce poi che le frequenze empiriche tenderanno a confermare la mia assegnazione iniziale.”

La differenza è profonda: nel primo caso, la probabilità viene definita attraverso il comportamento osservabile; nel secondo, invece, la probabilità esprime uno stato di conoscenza che permette di fare previsioni su ciò che verosimilmente osserveremo.

1.7.3 Simulazione come verifica di coerenza

Le simulazioni servono principalmente a convalidare che un sistema di credenze coerente genera comportamenti empirici attesi. Il loro ruolo è quello di illustrare concetti fondamentali come la convergenza statistica e la variabilità campionaria, nonché di confrontare le previsioni dei modelli probabilistici con i dati osservati.

È importante sottolineare che le simulazioni non definiscono la natura della probabilità, ma piuttosto verificano le implicazioni delle nostre assegnazioni probabilistiche, dimostrando come credenze razionali si traducano in regolarità osservabili.

1.7.4 Esempio: Lancio di moneta rivisitato

set.seed(42)

# Assegno credenza P(Testa) = 0.5 per simmetria epistemica
p_testa_credenza <- 0.5

# Simulazione: verifico che questa credenza è coerente
n_lanci <- 10000
risultati <- rbinom(n_lanci, 1, p_testa_credenza)

# Frequenza cumulativa
freq_cumulativa <- cumsum(risultati) / seq_along(risultati)

# Grafico
df <- data.frame(
  lancio = seq_along(risultati),
  freq = freq_cumulativa
)

ggplot(df, aes(x = lancio, y = freq)) +
  geom_line(alpha = 0.7) +
  geom_hline(yintercept = p_testa_credenza, 
             linetype = "dashed", color = "red", size = 1) +
  labs(
    title = "Frequenza cumulativa converge alla credenza",
    subtitle = "La credenza P(Testa)=0.5 predice la convergenza osservata",
    x = "Numero di lanci",
    y = "Frequenza cumulativa di Teste"
  ) +
  ylim(0.3, 0.7)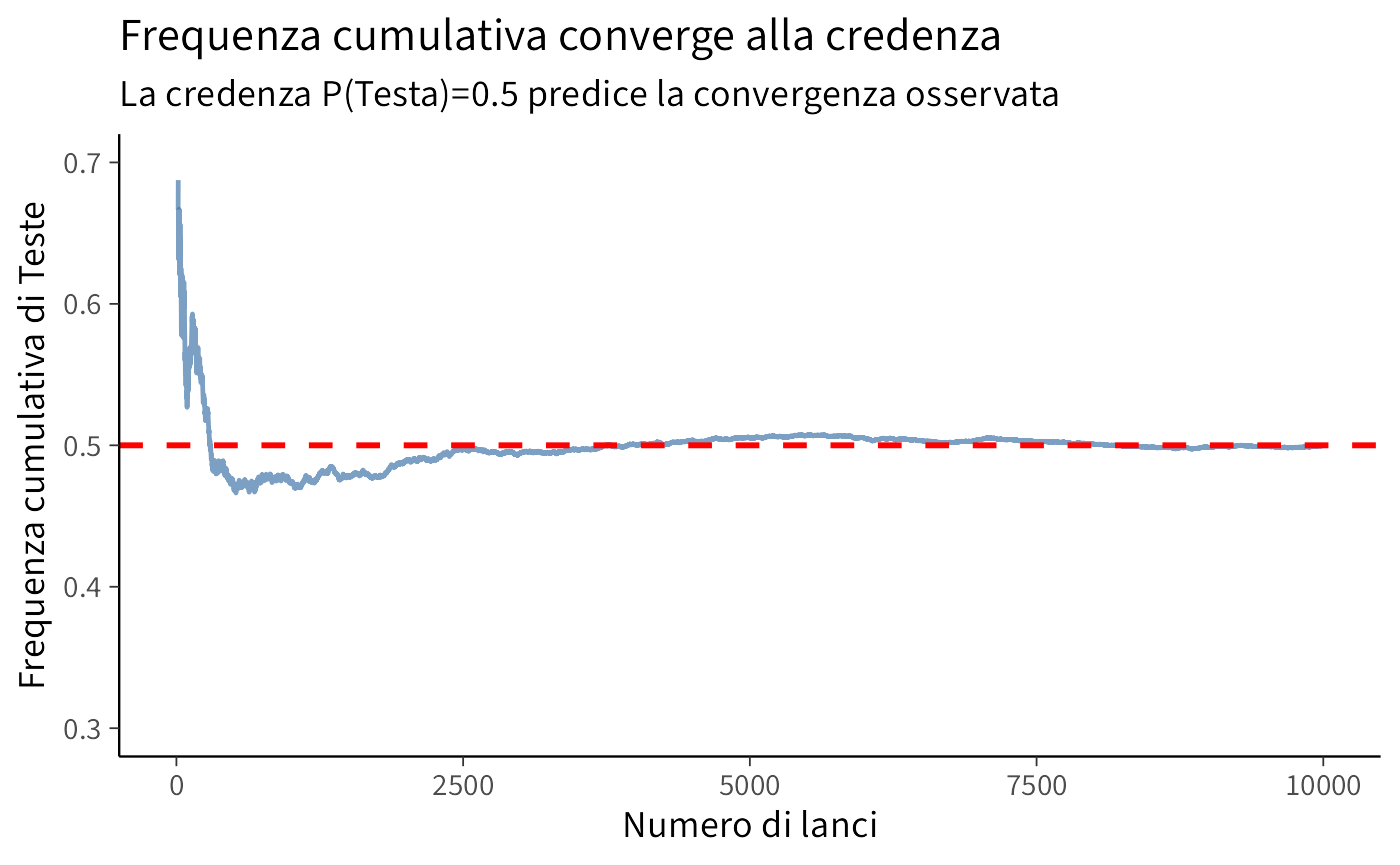

Interpretazione bayesiana: Abbiamo assegnato \(P(\text{Testa}) = 0.5\) per simmetria epistemica (nessuna ragione per favorire testa o croce). La simulazione verifica che questa credenza è coerente con la LLN: le frequenze convergono al valore atteso. Ma la probabilità 0.5 non è definita dalla convergenza—è stata assegnata prima, e la convergenza la conferma.

1.8 Prima introduzione all’aggiornamento bayesiano

1.8.1 Teorema di Bayes: dal concetto al test diagnostico

Il teorema di Bayes descrive come aggiornare una credenza iniziale \(P(H)\) sull’ipotesi \(H\) alla luce di una nuova evidenza \(E\):

\[ P(H \mid E) = \frac{P(E \mid H) , P(H)}{P(E)}. \]

Significato dei termini:

Simbolo	Nome	Interpretazione generale
\(P(H)\)	prior	Credenza iniziale nell’ipotesi
\(P(E \mid H)\)	verosimiglianza	Quanto è probabile osservare \(E\) se \(H\) è vera
\(P(E)\)	evidenza	Probabilità complessiva di osservare \(E\)
\(P(H \mid E)\)	posterior	Credenza aggiornata in \(H\) dopo aver visto \(E\)

1.8.1.1 Applicazione: il test diagnostico

Nel caso di un test medico, la struttura è identica, ma i simboli assumono un significato concreto:

Formula generale	Corrispondenza nel test diagnostico
\(H\)	“Il paziente ha la malattia” (\(D\))
\(\neg H\)	“Il paziente non ha la malattia” (\(\neg D\))
\(E\)	“Il test è positivo” (\(+\))
\(P(H)\)	\(P(D)\): prevalenza (probabilità a priori di essere malato)
\(P(E \mid H)\)	\(P(+ \mid D)\): sensibilità
\(P(E \mid \neg H)\)	\(P(+ \mid \neg D)\): tasso di falsi positivi
\(P(H \mid E)\)	\(P(D \mid +)\): probabilità di essere malato dopo un test positivo

Usando la notazione precedente, la formula di Bayes diventa:

\[ P(D \mid +) = \frac{P(+ \mid D) \, P(D)} {P(+ \mid D) \, P(D) + P(+ \mid \neg D) \, P(\neg D)}. \]

1.8.2 Esempio numerico

Supponiamo che:

• la prevalenza della condizione sia \(P(D\) = 0.10);
• la sensibilità del test sia \(P(+ \mid D\) = 0.80);
• la specificità sia \(P(- \mid \neg D) = 0.90\), quindi \(P(+ \mid \neg D) = 0.10\).

Vogliamo sapere: dopo un test positivo, qual è la probabilità di avere la malattia?

# Parametri del test
p_D   <- 0.10       # Prevalenza = prior P(D)
sens  <- 0.80       # Sensibilità = P(+ | D)
spec  <- 0.90       # Specificità = P(- | ~D)
p_pos_given_notD <- 1 - spec  # Falsi positivi P(+ | ~D)

# Probabilità complessiva di test positivo
p_pos <- sens * p_D + p_pos_given_notD * (1 - p_D)

# Teorema di Bayes: posterior
p_D_given_pos <- (sens * p_D) / p_pos

cat("P(D) =", p_D, "\n")
#> P(D) = 0.1
cat("P(D | +) =", round(p_D_given_pos, 3), "\n")
#> P(D | +) = 0.471

1.8.3 Interpretazione passo per passo

• Prima del test: credenza iniziale = prevalenza = 10%.
• Dopo un test positivo: la credenza aggiornata sale a 47%.
• Nonostante la buona sensibilità e specificità, resta una forte incertezza: su 100 test positivi, circa 53 sono falsi positivi.

1.8.4 Riepilogo concettuale

\[ \underbrace{P(D)}_{\text{prior}} \quad \xrightarrow[\text{aggiornamento con } P(+|D), P(+|\neg D)]{\text{osservazione del test positivo}} \quad \underbrace{P(D \mid +)}_{\text{posterior}} \]

Il teorema di Bayes mostra che la probabilità finale non dipende solo dalla qualità del test, ma anche da quanto la malattia era plausibile a priori. In termini psicologici, è il modello formale del ragionamento inferenziale: integrare l’informazione nuova con le conoscenze precedenti in modo coerente.

1.8.4.1 Visualizzazione con una tabella di contingenza

Per rendere concreto il ragionamento, immaginiamo una popolazione di 1000 persone.

• Il 10% (cioè 100 persone) ha la malattia.
• L’80% di queste (80 persone) risulterà positivo: veri positivi.
• Il 90% delle persone sane (900 persone) risulterà negativo, quindi il 10% (90 persone) darà un falso positivo.

Stato reale / Esito del test	Positivo	Negativo	Totale
Malato \(D\)	80	20	100
Sano \(¬D\)	90	810	900
Totale	170	830	1000

Tra i 170 test positivi, solo 80 appartengono a persone realmente malate.

\[ P(D \mid +) = \frac{80}{170} \approx 0.47. \]

Lo stesso valore ottenuto con la formula di Bayes.

1.8.5 Codice R per la simulazione e la tabella

# Parametri del test
p_D   <- 0.10       # Prevalenza = prior P(D)
sens  <- 0.80       # Sensibilità = P(+ | D)
spec  <- 0.90       # Specificità = P(- | ~D)
p_pos_given_notD <- 1 - spec  # Falsi positivi P(+ | ~D)

# Calcolo per 1000 persone
N <- 1000
malati <- N * p_D
sani   <- N * (1 - p_D)

veri_positivi  <- malati * sens
falsi_negativi <- malati * (1 - sens)
falsi_positivi <- sani * p_pos_given_notD
veri_negativi  <- sani * spec

tabella <- data.frame(
  `Stato reale` = c("Malato (D)", "Sano (¬D)", "Totale"),
  `Positivo` = c(veri_positivi, falsi_positivi, veri_positivi + falsi_positivi),
  `Negativo` = c(falsi_negativi, veri_negativi, falsi_negativi + veri_negativi),
  `Totale`   = c(malati, sani, N)
)
tabella
#>   Stato.reale Positivo Negativo Totale
#> 1  Malato (D)       80       20    100
#> 2   Sano (¬D)       90      810    900
#> 3      Totale      170      830   1000

1.8.6 Interpretazione visiva

La tabella mostra da dove viene il 47%:

• su 170 test positivi, 80 sono veri positivi e 90 falsi positivi;
• quindi, anche con un test buono, la maggioranza dei positivi può risultare non malata se la prevalenza è bassa.

1.8.7 Sintesi concettuale

Quantità	Formula	Valore	Significato
\(P(D)\)		0.10	Prevalenza (prior)
\(P(+ \mid D)\)		0.80	Sensibilità
\(P(+ \mid \neg D)\)		0.10	Falsi positivi
\(P(D \mid +)\)		0.47	Probabilità aggiornata (posterior)

Conclusione: Il teorema di Bayes ci permette di passare dal livello astratto delle probabilità condizionate alla rappresentazione concreta delle frequenze. Questa doppia lettura – formale e intuitiva – è ciò che rende Bayes uno strumento potente per comprendere come la mente (o un sistema razionale) aggiorna le credenze alla luce di nuove evidenze.

Questa è l’essenza del ragionamento bayesiano: aggiornamento sistematico e razionale delle credenze alla luce di nuove evidenze.

1.9 Il ruolo della probabilità nello studio dei fenomeni psicologici

La teoria della probabilità bayesiana fornisce un framework particolarmente adatto alla psicologia, offrendo strumenti concettuali e metodologici che rispondono alle esigenze specifiche della ricerca e della pratica clinica in questo campo.

1.9.1 Quantificare l’incertezza diagnostica

Nella pratica clinica, infatti, è raro disporre di certezze assolute. Un clinico che valuta un paziente deve integrare informazioni provenienti da fonti diverse, come l’anamnesi, l’osservazione comportamentale e i test psicometrici, ciascuna delle quali porta con sé un certo grado di incertezza. La probabilità bayesiana permette di quantificare esplicitamente l’incertezza delle diagnosi, fornendo un linguaggio matematico per esprimere il livello di fiducia in un’ipotesi diagnostica. Attraverso il teorema di Bayes, è possibile integrare in modo sistematico le informazioni provenienti da test multipli, ciascuno dei quali modifica le nostre credenze in modo coerente e trasparente. Particolarmente rilevante è la possibilità di considerare esplicitamente la prevalenza dei disturbi nella popolazione di riferimento, ovvero il cosiddetto “prior”, evitando errori diagnostici derivanti dall’ignorare i tassi base. Questo approccio consente inoltre di comunicare l’incertezza in modo chiaro e onesto sia ai colleghi sia ai pazienti, riconoscendo i limiti della conoscenza diagnostica senza rinunciare a quantificarla in modo rigoroso.

1.9.2 Modellare processi cognitivi

Un’area di ricerca sempre più influente suggerisce che la mente umana funzioni secondo principi fondamentalmente bayesiani. Nella percezione, ad esempio, il cervello sembra integrare costantemente le aspettative pregresse, basate su esperienze passate e regolarità ambientali, con l’input sensoriale del momento, proprio come farebbe un osservatore bayesiano ideale che combina prior e verosimiglianza. Questo framework spiega fenomeni come le illusioni percettive, in cui aspettative forti possono prevalere su segnali sensoriali deboli o ambigui. Anche l’apprendimento può essere concepito come un processo di aggiornamento bayesiano delle credenze attraverso l’esperienza: ogni nuova osservazione modifica la nostra comprensione del mondo in proporzione alla sua capacità di fornire informazioni. Nei processi decisionali, infine, il framework bayesiano offre un modello normativo su come dovremmo bilanciare evidenze incerte e obiettivi multipli. È interessante notare che molti bias cognitivi documentati nella letteratura psicologica, come l’effetto di ancoraggio o la conservatività nell’aggiornamento delle credenze, possono essere interpretati come deviazioni sistematiche dall’ottimalità bayesiana, fornendo ipotesi testabili sui meccanismi alla base del ragionamento umano.

1.9.3 Analizzare dati sperimentali

Dal punto di vista metodologico, l’inferenza bayesiana offre notevoli vantaggi per l’analisi dei dati psicologici. A differenza dell’approccio frequentista tradizionale, il framework bayesiano permette di incorporare formalmente le conoscenze pregresse derivanti da studi pilota, dalla letteratura esistente o da teorie consolidate, traducendole in distribuzioni a priori che guidano l’interpretazione dei nuovi dati. Questo è particolarmente prezioso in psicologia, dove raramente si parte da zero nella formulazione delle ipotesi. Un altro vantaggio cruciale riguarda la possibilità di quantificare l’evidenza a favore dell’ipotesi nulla, superando una limitazione fondamentale del valore-\(p\) che può solo rigettare, ma non confermare, l’assenza di un effetto. Inoltre, l’approccio bayesiano gestisce naturalmente i piccoli campioni, comuni nella ricerca clinica e in alcuni ambiti sperimentali, senza richiedere le approssimazioni asintotiche su cui si basano molti test frequentisti. Infine, nei modelli statistici complessi che caratterizzano sempre più la ricerca psicologica contemporanea, il framework bayesiano consente di propagare l’incertezza in modo coerente e sistematico attraverso tutti i livelli del modello, fornendo stime dell’incertezza più realistiche e informative.

1.9.4 Decisioni cliniche

In ambito terapeutico, l’approccio bayesiano fornisce strumenti utili per la pratica quotidiana. Quando valutiamo l’efficacia di trattamenti personalizzati, possiamo partire da evidenze generali sulla popolazione e aggiornarle progressivamente con le risposte specifiche del singolo paziente, ottenendo così una stima sempre più precisa dell’efficacia terapeutica per quella persona in particolare. Questo processo iterativo di aggiornamento consente anche di modificare i protocolli terapeutici man mano che emergono nuove evidenze, sia dalla letteratura che dall’esperienza clinica diretta, senza dover attendere la conclusione di revisioni sistematiche complete. Nelle decisioni che implicano rischi e benefici, come la scelta tra diverse opzioni farmacologiche o l’intensità di un intervento, il framework bayesiano fornisce strumenti formali per bilanciare probabilità e utilità in condizioni di incertezza, rendendo espliciti i trade-off impliciti in ogni decisione clinica. Quando si tratta di pianificare sequenze di interventi, in cui le decisioni successive dipendono dai risultati precedenti, l’aggiornamento bayesiano fornisce una guida naturale per ottimizzare il percorso terapeutico in modo adattivo e basato sull’evidenza.

1.10 Confronto con l’approccio frequentista

Per apprezzare appieno la prospettiva bayesiana, è utile chiarire le differenze fondamentali rispetto all’approccio frequentista, che ancora oggi domina gran parte della formazione statistica in psicologia. Le due scuole di pensiero divergono già dalla definizione stessa di probabilità. Secondo l’approccio frequentista, la probabilità è concepita come la frequenza limite di un evento in infinite repliche ipotetiche di un esperimento, mentre secondo l’approccio bayesiano rappresenta il grado di credenza razionale in base al nostro stato di informazione. Questa differenza filosofica ha profonde implicazioni pratiche.

Nel paradigma frequentista, i parametri di interesse, come la media di una popolazione o l’effetto di un trattamento, sono considerati quantità fisse, ma ignote, su cui non è possibile fare affermazioni probabilistiche dirette. Possiamo solo parlare delle proprietà delle procedure che utilizziamo per stimarle. Al contrario, nell’approccio bayesiano, i parametri sono trattati come variabili casuali caratterizzate da distribuzioni di probabilità che esprimono direttamente il nostro livello di incertezza riguardo a essi. Ciò consente di formulare affermazioni come “la probabilità che l’effetto del trattamento sia positivo è 0.85”, cosa impossibile da fare rigorosamente nel quadro frequentista.

L’inferenza stessa è concepita in modo diverso nei due paradigmi. L’approccio frequentista valuta le proprietà di procedure ripetute: un intervallo di confidenza al 95%, per esempio, è costruito in modo tale che, se si replicasse infinite volte lo stesso esperimento, il 95% degli intervalli così costruiti conterrebbe il valore effettivo del parametro. Tuttavia, questo non ci dice nulla sulla probabilità che un intervallo specifico, costruito sulla base dei dati osservati, contenga il parametro. L’approccio bayesiano, invece, produce intervalli di credibilità che hanno un’interpretazione probabilistica diretta: un intervallo al 95% contiene il parametro con probabilità 0.95, dati i risultati osservati.

Una distinzione cruciale riguarda il ruolo delle conoscenze pregresse. Nel framework frequentista non esiste un meccanismo formale che permetta di incorporare informazioni pregresse all’analisi dei dati correnti. L’approccio bayesiano, invece, considera le conoscenze pregresse, codificate nelle distribuzioni a priori, come un elemento essenziale e trasparente del processo inferenziale. Questo aspetto può essere considerato un vantaggio, in quanto rende esplicito ciò che, nella pratica, influenza comunque le nostre conclusioni, oppure una fonte di soggettività, a seconda della prospettiva.

Anche gli strumenti inferenziali differiscono sostanzialmente. Il p-value, pilastro dell’inferenza frequentista, quantifica la probabilità di osservare dati estremi quanto o più dei nostri, a condizione che l’ipotesi nulla sia vera. Si tratta di una probabilità condizionale che risponde alla domanda: “Quanto sarebbero sorprendenti questi dati se l’ipotesi nulla fosse vera?”. Tuttavia, questa non è la domanda che ci poniamo di solito: ci interessa piuttosto sapere quanto sia plausibile l’ipotesi nulla alla luce di questi dati. Una domanda a cui solo l’approccio bayesiano può rispondere direttamente. L’interpretazione bayesiana permette infatti di calcolare le probabilità a posteriori delle ipotesi, fornendo risposte più intuitive e direttamente rilevanti per le decisioni di natura scientifica e clinica.

NotaComplementarità degli approcci

Sebbene questo corso adotti la prospettiva bayesiana, sarebbe scorretto presentare i due paradigmi come mutuamente esclusivi o in conflitto insanabile. In molti contesti pratici, le due prospettive convergono verso conclusioni sostanzialmente simili, soprattutto quando i dati sono abbondanti e le distribuzioni a priori bayesiane sono sufficientemente vaghe da lasciare che siano i dati a parlare. Inoltre, i due approcci possono essere utilizzati in modo complementare all’interno dello stesso progetto di ricerca: l’approccio frequentista può garantire la stabilità delle procedure nel lungo periodo, mentre l’approccio bayesiano può fornire interpretazioni più dirette e contestualizzate dei risultati specifici ottenuti.

La scelta tra i due approcci dipende, in ultima analisi, dagli obiettivi della ricerca, dalla natura del problema e dalle risorse disponibili. Tuttavia, per sviluppare una comprensione coerente e approfondita della probabilità e dell’inferenza statistica, è pedagogicamente vantaggioso, se non necessario, adottare un approccio chiaro fin dall’inizio e mantenerlo con coerenza nel percorso formativo. In questo testo, abbiamo scelto la prospettiva bayesiana non perché sia l’unica legittima, ma perché offre un framework concettualmente unificato particolarmente adatto alle domande che ci poniamo tipicamente in psicologia, dove l’incertezza è onnipresente, i campioni spesso limitati e l’integrazione di diverse fonti di conoscenza è essenziale per prendere decisioni informate.

Riflessioni conclusive

In questo capitolo, abbandoniamo la concezione della probabilità come semplice “frequenza relativa” per abbracciarne una più potente e generale: la probabilità come “grado di credenza razionale”. Questa prospettiva, radicata nella tradizione di Bayes, Laplace e De Finetti, non è solo un tecnicismo matematico, ma una lente attraverso cui interpretare il ragionamento umano in situazioni di incertezza. Perché è così rilevante per la psicologia?

Questa impostazione epistemica offre cinque vantaggi fondamentali:

1. Fondazione logica, non empirica: gli assiomi della probabilità diventano vincoli di coerenza logica per le nostre convinzioni. Non si tratta di leggi naturali da verificare sperimentalmente, ma di principi di razionalità che, se violati, portano a contraddizioni.

2. Massima generalità: possiamo quantificare l’incertezza relativa a eventi unici e non ripetibili; Domande come “Questo specifico paziente guarirà?” o “Questa teoria è vera?” trovano una risposta formale senza bisogno di un ipotetico esperimento ripetuto all’infinito.

3. Completa trasparenza: tutte le nostre assunzioni iniziali (le probabilità a priori) sono esplicite e messe in discussione. Questo favorisce un dialogo scientifico più rigoroso, in cui non ci si nasconde dietro un’illusoria “oggettività”.

4. Apprendimento dinamico: il teorema di Bayes formalizza matematicamente il processo di apprendimento dall’esperienza. Esso mostra come le nostre credenze si evolvono e si affinano man mano che raccogliamo nuovi dati.

5. Aderenza al ragionamento umano: questo approccio rispecchia in modo più fedele il modo in cui la nostra mente valuta i rischi e prende decisioni in condizioni di informazione incompleta.

Nei prossimi capitoli costruiremo gli strumenti formali di questo quadro teorico, dagli assiomi al concetto fondamentale di probabilità condizionata, restando sempre fedeli a questa prospettiva. Scopriremo, ad esempio, che nozioni come l’equiprobabilità non sono proprietà intrinseche del mondo, ma riflettono una simmetria nelle nostre informazioni.

La probabilità bayesiana non elimina l’incertezza, ma la quantifica e la gestisce razionalmente. È questo il suo grande valore per la ricerca psicologica, dove l’incertezza è la norma, non l’eccezione.

ConsiglioLetture consigliate

Per chi desidera approfondire:

• De Finetti, B. (1974). Theory of Probability. Wiley. [Classico sulla probabilità soggettivista]
• Jaynes, E. T. (2003). Probability Theory: The Logic of Science. Cambridge University Press. [Approccio assiomatico alla probabilità epistemica]
• Clayton, A. (2021). Bernoulli’s Fallacy. Columbia University Press. [Storia accessibile della controversia frequentismo-bayesiano]
• Spiegelhalter, D. (2024). The Art of Uncertainty. Penguin. [Applicazioni moderne della probabilità all’incertezza quotidiana]

Esercizi

ImportanteProblemi

1.10.1 Esercizi concettuali

1. Spiega la differenza tra probabilità come frequenza relativa e probabilità come grado di credenza. In quale contesto psicologico questa differenza è particolarmente rilevante?

2. Cos’è un Dutch Book? Perché l’argomento del Dutch Book giustifica gli assiomi della probabilità?

3. Due psicologi assegnano probabilità diverse allo stesso evento (es. efficacia di un nuovo trattamento). Entrambi usano l’approccio bayesiano. Questo è un problema per la teoria bayesiana? Perché?

4. La Legge dei Grandi Numeri gioca un ruolo diverso nell’approccio bayesiano rispetto al frequentista. Spiega questa differenza.

5. Considera l’affermazione: “La probabilità che piova domani è 0.7”. Interpreta questa frase dal punto di vista bayesiano e poi da quello frequentista. Quale interpretazione è più naturale?

1.10.2 Esercizi sulla coerenza

6. Verifica se le seguenti assegnazioni sono coerenti per eventi mutuamente esclusivi ed esaustivi:

   • \(P(A) = 0.4\), \(P(B) = 0.3\), \(P(C) = 0.3\)
   • \(P(A) = 0.5\), \(P(B) = 0.5\), \(P(C) = 0.2\)

7. Un clinico assegna le seguenti probabilità per tre diagnosi mutuamente esclusive:

   • Depressione: 0.6
   • Ansia: 0.4
   • Nessuna condizione: 0.3

   Identifica l’incoerenza e proponi una correzione.

8. Scrivi un breve script R per verificare se un insieme di probabilità su eventi disgiunti rispetta l’assioma di additività.

1.10.3 Esercizi su simulazioni

9. Simula 1000 lanci di una moneta con \(P(\text{Testa}) = 0.6\) (moneta sbilanciata). Visualizza la convergenza della frequenza cumulativa. La convergenza “definisce” la probabilità 0.6 o la verifica?

10. Un test di ansia ha sensibilità 0.85 e specificità 0.80. La prevalenza è 0.15. Calcola \(P(\text{Ansia} \mid \text{Test positivo})\) usando il teorema di Bayes, poi verifica il risultato con una simulazione Monte Carlo.

1.10.4 Esercizi di pensiero critico

11. Un frequentista afferma: “Non possiamo assegnare probabilità all’evento ‘L’Italia vincerà i prossimi Mondiali’ perché non è ripetibile”. Come risponderebbe un bayesiano?

12. Perché nell’approccio bayesiano è essenziale distinguere tra incertezza epistemica e ontologica, anche se entrambe vengono modellate con probabilità?

13. In un esperimento psicologico, due ricercatori partono con prior diversi sullo stesso parametro. Dopo aver osservato molti dati, i loro posterior convergono. Cosa ci dice questo sulla relazione tra soggettività e oggettività nell’inferenza bayesiana?

14. La frase “La probabilità non esiste” di de Finetti sembra paradossale per una teoria della probabilità. Cosa intendeva de Finetti?

15. Considera un paziente che ha avuto un test positivo per una condizione rara. Il medico dice: “Il test ha sensibilità 99%, quindi c’è il 99% di probabilità che tu abbia la condizione”. Identifica l’errore dal punto di vista bayesiano.

ConsiglioSoluzioni

1.10.5 Soluzioni agli esercizi concettuali

1. Frequenza vs credenza: La frequenza relativa definisce la probabilità come limite di frequenze in infinite repliche identiche dell’esperimento. La credenza bayesiana quantifica incertezza dato lo stato d’informazione attuale. In psicologia clinica, quando valutiamo “la probabilità che questo specifico paziente risponda al trattamento”, l’interpretazione frequentista è problematica (un paziente non è “replicabile”), mentre quella bayesiana è naturale.

2. Dutch Book: È una combinazione di scommesse che garantisce perdita certa. Se le probabilità violano gli assiomi, si possono costruire Dutch Books contro chi le ha assegnate. Questo argomento mostra che gli assiomi non sono arbitrari, ma necessari per evitare contraddizioni pragmatiche nelle decisioni sotto incertezza.

3. Soggettività non è problema: Nel bayesianesimo, credenze diverse sono legittime se riflettono informazioni diverse. Con gli stessi dati, due bayesiani con prior diversi convergeranno verso posterior simili. La soggettività è nelle assunzioni iniziali (esplicite), non nell’aggiornamento (che segue regole oggettive).

4. LLN: Per il frequentista, la LLN definisce la probabilità come limite delle frequenze. Per il bayesiano, la LLN spiega perché frequenze empiriche convergono alla credenza iniziale—verifica coerenza, non definisce il concetto.

5. Pioggia domani:

   • Bayesiano: “Dato ciò che so (previsioni, stagione, clima locale), assegno credenza 0.7 all’evento pioggia domani”
   • Frequentista: “In infiniti ‘domani’ identici a questo, pioverebbe nel 70% dei casi” (problematico: domani non è replicabile!)

   L’interpretazione bayesiana è più naturale per eventi singoli.

1.10.6 Soluzioni agli esercizi sulla coerenza

6. Prima assegnazione: \(0.4 + 0.3 + 0.3 = 1.0\) ✓ Coerente
   Seconda assegnazione: \(0.5 + 0.5 + 0.2 = 1.2 > 1\) ✗ Incoerente

7. Somma: \(0.6 + 0.4 + 0.3 = 1.3 > 1\). Incoerente! Possibile correzione (normalizzando):

   • Depressione: \(0.6/1.3 \approx 0.46\)
   • Ansia: \(0.4/1.3 \approx 0.31\)
   • Nessuna condizione: \(0.3/1.3 \approx 0.23\)

8. Script R:

check_coherence <- function(probs, tolerance = 1e-9) {
  s <- sum(probs)
  if (abs(s - 1) < tolerance) {
    cat("✓ Coerente: somma =", s, "\n")
    return(TRUE)
  } else {
    cat("✗ Incoerente: somma =", s, "\n")
    return(FALSE)
  }
}

# Test
check_coherence(c(0.4, 0.3, 0.3))
check_coherence(c(0.5, 0.5, 0.2))

1.10.7 Soluzioni esercizi su simulazioni

9. La convergenza verifica la credenza 0.6, non la definisce. Abbiamo assegnato 0.6 prima di simulare, e la simulazione conferma che questa assegnazione è coerente con il comportamento atteso.

10. Calcolo analitico: \[P(\text{Ansia} \mid +) = \frac{0.85 \times 0.15}{0.85 \times 0.15 + 0.20 \times 0.85} = \frac{0.1275}{0.2975} \approx 0.43\]

Verifica Monte Carlo:

set.seed(42)
n <- 1e6
ansia <- rbinom(n, 1, 0.15)
test <- ifelse(ansia == 1, 
               rbinom(n, 1, 0.85),
               rbinom(n, 1, 0.20))
mean(ansia[test == 1])  # ≈ 0.43

1.10.8 Soluzioni esercizi di pensiero critico

11. Risposta bayesiana: “Posso assegnare credenza basandomi su tutto ciò che so: performance passate, rosa giocatori, probabilisti, contesto. Non serve replicabilità fisica—serve razionalità epistemica.”

12. Distinguere le due serve per capire che anche l’incertezza “ontologica” è modellata epistemicamente. La casualità intrinseca di un processo è indistinguibile, per noi osservatori limitati, dall’ignoranza sul suo stato. Il bayesianesimo adotta una posizione epistemica unificata.

13. La convergenza dei posterior mostra che, con sufficiente evidenza, l’influenza dei prior soggettivi si diluisce. L’oggettività emerge non dall’assenza di soggettività, ma dal peso crescente dei dati condivisi.

14. De Finetti intendeva che la probabilità non è una proprietà del mondo fisico, ma uno strumento epistemico. “Non esiste” nel senso ontologico, ma “esiste” come struttura logica per quantificare incertezza.

15. Il medico confonde \(P(\text{Test+} \mid \text{Malattia}) = 0.99\) (sensibilità) con \(P(\text{Malattia} \mid \text{Test+})\) (valore predittivo positivo). Con condizione rara, anche test eccellente produce molti falsi positivi. Serve usare Bayes incorporando la prevalenza!

Bibliografia

Spiegelhalter, D. (2024). Why probability probably doesn’t exist (but it is useful to act like it does). Nature, 636(8043), 560–563.