here::here("code", "_common.R") |>
source()
# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(ggplot2, dplyr, tidyr, patchwork, ggforce, DiagrammeR)4 Probabilità condizionata come aggiornamento
“Probability is always conditional.”
– Dennis V. Lindley, The Philosophy of Statistics (2000).
Introduzione
La probabilità condizionata è il meccanismo fondamentale attraverso cui le credenze si aggiornano alla luce di nuove informazioni. Quando apprendiamo che si è verificato un evento \(B\), la nostra credenza su un altro evento \(A\) deve cambiare in modo coerente: questo cambiamento è quantificato dalla probabilità condizionata \(P(A|B)\).
Da una prospettiva bayesiana, ogni probabilità è implicitamente condizionata allo stato di informazione corrente. Quando diciamo \(P(A)\), stiamo in realtà dicendo \(P(A \mid \mathcal{I})\), dove \(\mathcal{I}\) rappresenta tutto ciò che sappiamo. La probabilità condizionata formalizza il processo di riduzione dello spazio epistemico: apprendere l’evento \(B\) significa restringere le possibilità a quelle compatibili con esso e ricalibrare le credenze di conseguenza.
In questo capitolo esploreremo la probabilità condizionata non come un’operazione tecnica su insiemi, ma come una regola di coerenza per l’aggiornamento delle credenze. Vedremo come questo concetto sia fondamentale per comprendere l’indipendenza, il teorema del prodotto, la legge della probabilità totale e, nel prossimo capitolo, il teorema di Bayes.
Panoramica del capitolo
- Probabilità condizionata come riduzione dello spazio epistemico.
- Interpretazione epistemica dell’aggiornamento.
- Indipendenza come assenza di informazione reciproca.
- Teorema del prodotto e probabilità congiunta.
- Legge della probabilità totale.
- Paradosso di Simpson.
- Applicazioni a diagnostica clinica e test psicologici.
4.1 Definizione e interpretazione epistemica
Definizione 4.1 (Probabilità condizionata) Se \(P(B) > 0\), la probabilità condizionata di \(A\) dato \(B\) è definita come:
\[ P(A \mid B) = \frac{P(A \cap B)}{P(B)} \tag{4.1}\]
Interpretazione epistemica: \(P(A \mid B)\) quantifica il nostro grado di credenza in \(A\) dopo aver appreso che \(B\) è vero, tenendo conto del fatto che ora lo spazio delle possibilità si è ristretto a quelle compatibili con \(B\).
4.1.1 Perché questa formula?
La definizione di probabilità condizionata non è una convenzione arbitraria, ma emerge come conseguenza necessaria del principio di coerenza probabilistica. Consideriamo una distribuzione di probabilità congiunta rappresentata da una tabella 2 \(\times\) 2:
| \(B\) | \(B^c\) | Marginali | |
|---|---|---|---|
| \(A\) | \(p_{11}\) | \(p_{12}\) | \(P(A)\) |
| \(A^c\) | \(p_{21}\) | \(p_{22}\) | \(P(A^c)\) |
| Marginali | \(P(B)\) | \(P(B^c)\) | \(1\) |
Quando si acquisisce l’informazione che l’evento \(B\) si è verificato, lo spazio probabilistico si riduce alla sola colonna corrispondente a \(B\). Per preservare la coerenza interna del nostro sistema di credenze, dobbiamo implementare due operazioni fondamentali. In primo luogo, è necessario eliminare tutti gli esiti incompatibili con \(B\), ovvero quelli situati nella colonna \(B^c\). In secondo luogo, dobbiamo rinormalizzare le credenze residue, assicurando che la probabilità totale dello spazio ridotto sia pari a 1. Questa rinormalizzazione si ottiene dividendo ciascuna probabilità residua per \(P(B)\).
Il risultato di questo processo è la formula della probabilità condizionata: \[ P(A \mid B) = \frac{p_{11}}{p_{11} + p_{21}} = \frac{p_{11}}{P(B)} = \frac{P(A \cap B)}{P(B)}. \]
4.1.2 Visualizzazione geometrica
# Esempio con diagramma di Venn simulato
# Parametri
P_A <- 0.6
P_B <- 0.5
P_AB <- 0.35
# Creare dataframe per visualizzazione
df_venn <- data.frame(
x = c(0.3, 0.7),
y = c(0.5, 0.5),
r = c(sqrt(P_A / pi), sqrt(P_B / pi)),
label = c("A", "B")
)
# Calcolare condizionata
P_A_given_B <- P_AB / P_B
ggplot() +
geom_circle(data = df_venn, aes(x0 = x, y0 = y, r = r, fill = label),
alpha = 0.3, size = 1, show.legend = FALSE) +
annotate("text", x = 0.3, y = 0.85, label = "A", size = 8) +
annotate("text", x = 0.7, y = 0.85, label = "B", size = 8) +
annotate("text", x = 0.5, y = 0.5, label = "A ∩ B", size = 6) +
annotate("text", x = 0.5, y = -0.1,
label = sprintf("P(A|B) = P(A∩B)/P(B) = %.2f/%.2f = %.2f",
P_AB, P_B, P_A_given_B),
size = 5) +
coord_fixed() +
theme_void() +
labs(title = "Probabilità condizionata come riduzione dello spazio",
subtitle = "Apprendere B significa focalizzarsi sulla regione B e rinormalizzare")
4.2 Proprietà della probabilità condizionata
Le probabilità condizionate mantengono le proprietà degli assiomi, trattando \(B\) come nuovo “universo”.
Teorema 4.1 (Proprietà della condizionata) Fissato un evento \(B\) con \(P(B) > 0\), la funzione \(P(\cdot \mid B)\) soddisfa tutti gli assiomi della probabilità.
Non-negatività: \(P(A \mid B) \geq 0\) per ogni evento \(A\).
Normalizzazione: \(P(B \mid B) = 1\) (certezza di \(B\) dato \(B\)).
Additività: se \(A_1, A_2\) sono eventi disgiunti, allora \[P(A_1 \cup A_2 \mid B) = P(A_1 \mid B) + P(A_2 \mid B).\]
Complemento: \(P(A^c \mid B) = 1 - P(A \mid B).\)
Regola della catena (o del prodotto): \[P(A \cap B \mid C) = P(A \mid B \cap C) \cdot P(B \mid C).\]
Dimostrazione della proprietà 3 (additività): \[ P(A_1 \cup A_2 \mid B) = \frac{P((A_1 \cup A_2) \cap B)}{P(B)} = \frac{P((A_1 \cap B) \cup (A_2 \cap B))}{P(B)} \]
Poiché \(A_1, A_2\) disgiunti, anche \(A_1 \cap B\) e \(A_2 \cap B\) lo sono: \[ = \frac{P(A_1 \cap B) + P(A_2 \cap B)}{P(B)} = \frac{P(A_1 \cap B)}{P(B)} + \frac{P(A_2 \cap B)}{P(B)} = P(A_1 \mid B) + P(A_2 \mid B). \]
NotaEsempio clinico completo
Test di screening per il disturbo depressivo maggiore
Contesto clinico: uno psicologo utilizza un test di screening per il disturbo depressivo maggiore in un contesto di comunità, caratterizzato da una popolazione non selezionata.
Informazioni epidemiologiche disponibili:
- prevalenza nella popolazione (distribuzione a priori): \(P(D) = 0.08\) (l’8% degli individui in contesto di comunità presenta il disturbo);
- sensibilità del test: \(P(T^+ \mid D) = 0.85\) (l’85% dei soggetti depressi risulta positivo al test);
- specificità del test: \(P(T^- \mid D^c) = 0.90\) (il 90% dei soggetti non depressi risulta negativo al test).
Costruzione della distribuzione di probabilità congiunta:
# Parametri epidemiologici
P_D <- 0.08
sens <- 0.85
spec <- 0.90
# Tassi di classificazione errata
fp_rate <- 1 - spec # P(T+ | D^c) = 0.10
# Probabilità congiunte
P_D_and_Tpos <- sens * P_D
P_D_and_Tneg <- (1 - sens) * P_D
P_Dc_and_Tpos <- fp_rate * (1 - P_D)
P_Dc_and_Tneg <- spec * (1 - P_D)
# Rappresentazione tabellare
tab_diagnostic <- matrix(
c(P_D_and_Tpos, P_D_and_Tneg,
P_Dc_and_Tpos, P_Dc_and_Tneg),
nrow = 2, byrow = TRUE,
dimnames = list(
Stato = c("D", "D^c"),
Test = c("T+", "T-")
)
)
cat("DISTRIBUZIONE DI PROBABILITÀ CONGIUNTA (Test × Stato):\n")
#> DISTRIBUZIONE DI PROBABILITÀ CONGIUNTA (Test × Stato):
print(round(tab_diagnostic, 4))
#> Test
#> Stato T+ T-
#> D 0.068 0.012
#> D^c 0.092 0.828
# Probabilità marginali
cat("\nPROBABILITÀ MARGINALI:\n")
#>
#> PROBABILITÀ MARGINALI:
cat("P(D) =", round(rowSums(tab_diagnostic)[1], 4), "\n")
#> P(D) = 0.08
cat("P(T+) =", round(colSums(tab_diagnostic)[1], 4), "\n")
#> P(T+) = 0.16
cat("P(T-) =", round(colSums(tab_diagnostic)[2], 4), "\n")
#> P(T-) = 0.84Questioni cliniche risolte mediante probabilità condizionate:
# 1. Valore predittivo positivo: P(D | T+)
P_Tpos <- colSums(tab_diagnostic)[1]
P_D_given_Tpos <- tab_diagnostic[1, 1] / P_Tpos
# 2. Valore predittivo negativo: P(D^c | T-)
P_Tneg <- colSums(tab_diagnostic)[2]
P_Dc_given_Tneg <- tab_diagnostic[2, 2] / P_Tneg
# 3. Probabilità residua di depressione dopo test negativo
P_D_given_Tneg <- tab_diagnostic[1, 2] / P_Tneg#> ANALISI DELL'AGGIORNAMENTO DELLE CREDENZE
#> =========================================
#> STATO DELLE CREDENZE PRIMA DEL TEST (distribuzione a priori):
#> P(D) = 0.08
#> STATO DELLE CREDENZE DOPO TEST POSITIVO:
#> P(D | T+) = 0.425 (Valore Predittivo Positivo)
#> Aggiornamento: la credenza aumenta da 0.08 a 0.425
#> STATO DELLE CREDENZE DOPO TEST NEGATIVO:
#> P(D | T-) = 0.0143
#> P(D^c | T-) = 0.986 (Valore Predittivo Negativo)
#> Aggiornamento: la credenza diminuisce da 0.08 a 0.0143Interpretazione epistemica del processo inferenziale.
La distribuzione a priori (prima della somministrazione del test) assegna una probabilità di \(P(D) = 0.08\) basandosi esclusivamente sui dati di prevalenza nella popolazione.
In seguito a un test positivo, l’informazione osservata determina un aggiornamento delle credenze portando a \(P(D \mid T^+) \approx 0.43\). È fondamentale notare che questo valore non corrisponde alla sensibilità del test (0.85), poiché la sensibilità quantifica \(P(T^+ \mid D)\) mentre il valore predittivo positivo rappresenta \(P(D \mid T^+)\). Il valore predittivo positivo dipende criticamente dal tasso base della condizione nella popolazione di riferimento.
In seguito a un test negativo, l’informazione osservata produce una drastica riduzione della credenza nella presenza del disturbo, portando a \(P(D \mid T^-) \approx 0.013\). L’elevata specificità del test rende un risultato negativo particolarmente informativo per escludere la condizione.
Visualizzazione dell’aggiornamento.
Verifica con simulazione Monte Carlo.
set.seed(123)
N <- 100000
# Simulare stato reale e risultato test
stato <- rbinom(N, 1, P_D) # 1 = Depresso, 0 = Non depresso
test_result <- ifelse(stato == 1,
rbinom(N, 1, sens), # Se depresso, test+ con prob sens
rbinom(N, 1, fp_rate)) # Se non depresso, test+ con prob fp_rate
# Calcolare condizionate empiriche
P_D_given_Tpos_sim <- mean(stato[test_result == 1] == 1)
P_D_given_Tneg_sim <- mean(stato[test_result == 0] == 1)#> === VERIFICA CON SIMULAZIONE ===
#> Teorico vs Simulato (N = 100000 ):
#> P(D | T+):
#> Teorico: 0.425
#> Simulato: 0.418
#> P(D | T-):
#> Teorico: 0.0143
#> Simulato: 0.01394.3 Indipendenza stocastica
Il concetto di indipendenza rappresenta una proprietà fondamentale che caratterizza l’assenza di relazione informativa tra eventi nell’ambito del ragionamento probabilistico.
Definizione 4.2 (Indipendenza (definizione epistemica)) Due eventi \(A\) e \(B\) sono indipendenti (notazione: \(A \perp B\)) quando l’acquisizione di informazione riguardante uno dei due eventi non modifica le nostre credenze relative all’altro:
\[ P(A \mid B) = P(A) \quad \text{e equivalentemente} \quad P(B \mid A) = P(B). \tag{4.2}\]
Conseguenza matematica: Se \(A \perp B\), allora la loro probabilità congiunta ammette una fattorizzazione moltiplicativa: \[ P(A \cap B) = P(A) \cdot P(B) \tag{4.3}\]
Interpretazione epistemica: l’informazione che “\(B\) si è verificato” non modifica la nostra credenza riguardo al verificarsi di \(A\). Gli eventi sono epistemicamente disgiunti: la conoscenza di uno non fornisce alcuna informazione utile né per prevedere il verificarsi dell’altro né per determinarne la probabilità.
4.3.1 Test di indipendenza nella tabella congiunta
Data una distribuzione di probabilità congiunta rappresentata in forma tabellare, è possibile verificare l’eventuale indipendenza tra due eventi confrontando due quantità specifiche:
- la probabilità congiunta osservata: \(P(A \cap B)\);
- il prodotto delle probabilità marginali: \(P(A) \cdot P(B)\).
Se queste due quantità coincidono, a meno di trascurabili errori di approssimazione numerica, possiamo concludere che gli eventi \(A\) e \(B\) sono statisticamente indipendenti.
#> Test di indipendenza:
#> P(D ∩ T+) osservata = 0.068
#> P(D) × P(T+) = 0.0128
#> Differenza: 0.0552
#> → Eventi DIPENDENTI (correlati)
#> Questo è atteso: il test è progettato per essere informativo sulla depressione!Osservazione: se il test e lo stato fossero indipendenti, il test sarebbe inutile (non fornirebbe alcuna informazione). La dipendenza è auspicabile per un test diagnostico efficace!
4.3.2 Indipendenza vs disgiunzione
# Esempio numerico
# A = "Lancio dado, esce numero pari"
# B = "Lancio dado, esce numero dispari"
# Disgiunti ma NON indipendenti
P_pari <- 3/6
P_dispari <- 3/6
P_pari_e_dispari <- 0 # Disgiunti!#> Eventi disgiunti (pari vs dispari):
#> P(Pari) = 0.5
#> P(Dispari) = 0.5
#> P(Pari ∩ Dispari) = 0
#> P(Pari) × P(Dispari) = 0.25
#>
#> P(Pari | Dispari) = 0 (se dispari è vero, pari è impossibile)
#> → Informazione totale: MASSIMA dipendenza!4.4 Teorema del prodotto (regola della catena)
Il teorema del prodotto fornisce un metodo alternativo, spesso più intuitivo, per esprimere le probabilità congiunte attraverso una scomposizione sequenziale.
Teorema 4.2 (Teorema del prodotto) Per due eventi \(A\) e \(B\) con \(P(B) > 0\) vale la relazione:
\[ P(A \cap B) = P(A \mid B) \cdot P(B) \tag{4.4}\]
Generalizzazione a \(n\) eventi: \[ P(A_1 \cap A_2 \cap \cdots \cap A_n) = P(A_1) \cdot P(A_2 \mid A_1) \cdot P(A_3 \mid A_1 \cap A_2) \cdots P(A_n \mid A_1 \cap \cdots \cap A_{n-1}). \]
Interpretazione epistemica: la costruzione della probabilità congiunta avviene attraverso un processo sequenziale di aggiornamento delle credenze. Si inizia con \(P(A_1)\) (credenza iniziale sul primo evento), poi si procede con l’aggiornamento sequenziale di ogni evento successivo alla luce degli eventi già condizionanti.
4.5 Legge della probabilità totale
La legge della probabilità totale costituisce un’applicazione fondamentale del teorema del prodotto in contesti in cui lo spazio campionario risulta suddiviso in scenari mutualmente esclusivi.
Teorema 4.3 (Legge della probabilità totale) Sia \(\{B_1, B_2, \ldots, B_n\}\) una partizione di \(\Omega\)—ovvero una collezione di eventi mutualmente esclusivi ed esaustivi che ricoprono l’intero spazio campionario. Allora, per ogni evento \(A\):
\[ P(A) = \sum_{i=1}^{n} P(A \mid B_i) \cdot P(B_i). \tag{4.5}\]
Interpretazione epistemica: la credenza complessiva nell’evento \(A\) corrisponde a una media ponderata delle credenze condizionate a ciascuno scenario \(B_i\), dove i pesi sono rappresentati dalle nostre credenze iniziali nei diversi scenari.
Dimostrazione: \[ \begin{aligned} P(A) &= P(A \cap \Omega) \\ &= P\left(A \cap \bigcup_{i=1}^{n} B_i\right) \quad \text{(per esaustività della partizione)} \\ &= \sum_{i=1}^{n} P(A \cap B_i) \quad \text{(per additività sugli eventi disgiunti)} \\ &= \sum_{i=1}^{n} P(A \mid B_i) \cdot P(B_i) \quad \text{(per il teorema del prodotto)} \end{aligned} \]
4.5.1 Visualizzazione con albero probabilistico
# Esempio: Probabilità di test positivo considerando due popolazioni
# Scenario: Clinica vs Popolazione generale
P_clinica <- 0.30 # 30% pazienti da clinica specialistica
P_pop_gen <- 0.70 # 70% da popolazione generale
# Prevalenze diverse
P_D_given_clinica <- 0.40
P_D_given_popgen <- 0.05
# Caratteristiche del test
sens <- 0.85 # Sensibilità
spec <- 0.90 # Specificità
fp_rate <- 1 - spec # Tasso falsi positivi = 0.10
# P(T+ | Clinica)
P_Tpos_given_clinica <- sens * P_D_given_clinica + fp_rate * (1 - P_D_given_clinica)
# P(T+ | Pop.Gen.)
P_Tpos_given_popgen <- sens * P_D_given_popgen + fp_rate * (1 - P_D_given_popgen)
# Probabilità totale di test positivo
P_Tpos_total <- P_Tpos_given_clinica * P_clinica + P_Tpos_given_popgen * P_pop_gen#> === LEGGE DELLA PROBABILITÀ TOTALE ===
#> Partizione dello spazio:
#> P(Clinica) = 0.3
#> P(Pop.Gen.) = 0.7
#> Probabilità condizionate:
#> P(T+ | Clinica) = 0.4
#> P(T+ | Pop.Gen.) = 0.137
#> Probabilità totale:
#> P(T+) = 0.216
#> = 0.4 × 0.3 + 0.137 × 0.7#>
#> Struttura ad albero:
#> [Popolazione Totale]
#> / \
#> / \
#> Clinica (0.3) Pop.Gen. (0.7)
#> | |
#> T+ (0.36) T+ (0.13)
#> |
#> P(T+) totale = 0.36×0.3 + 0.13×0.7 = 0.204.6 Paradosso di Simpson
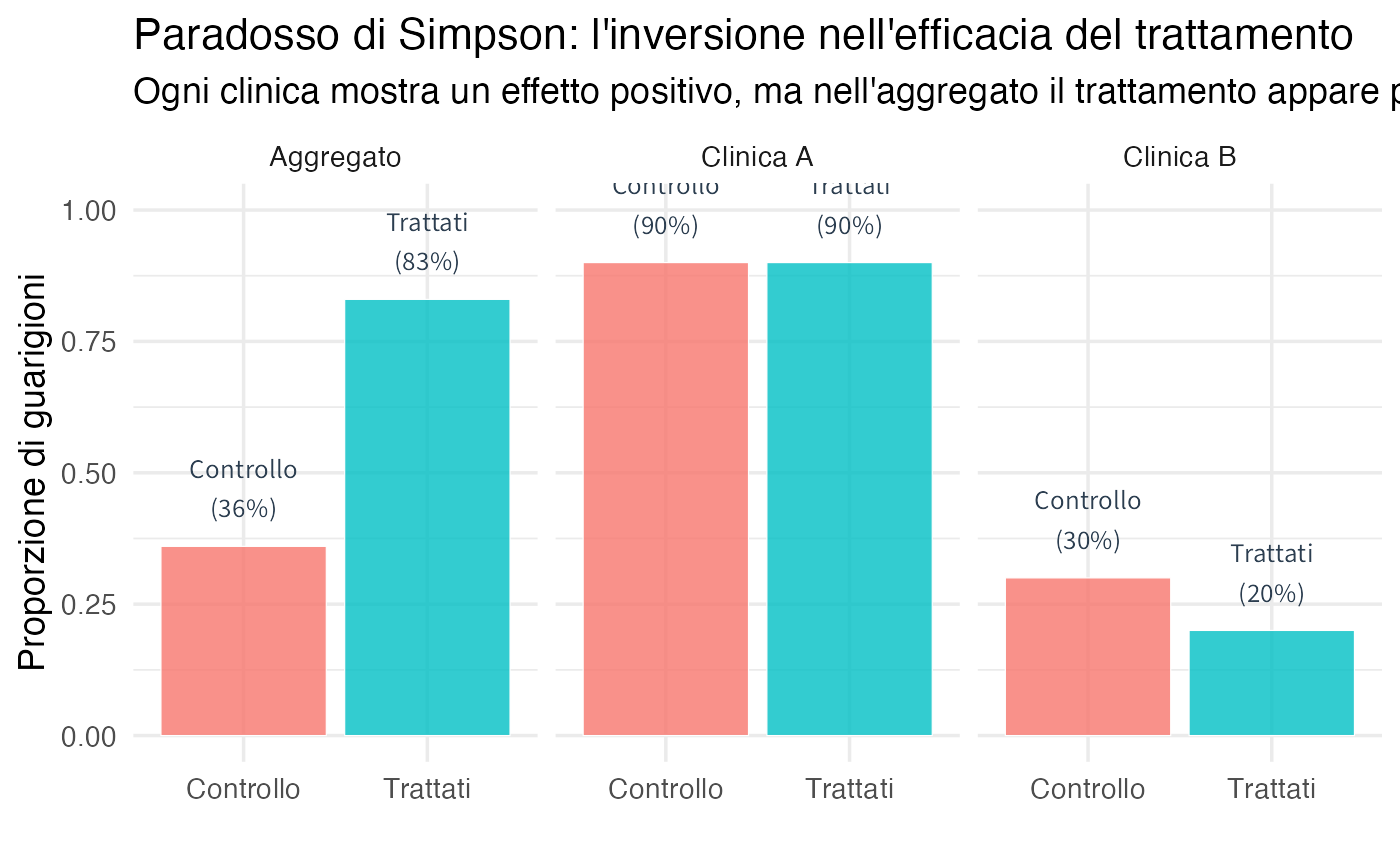
Il paradosso di Simpson mostra che una relazione osservata tra due variabili può invertire direzione quando si analizzano separatamente i sottogruppi della popolazione. Ciò avviene quando una variabile confondente (ad esempio la gravità del caso o il sesso dei partecipanti) influenza sia l’esposizione sia l’esito.
NotaEsempio
Efficacia del trattamento per la depressione in due cliniche
Due cliniche (A e B) valutano un nuovo trattamento per la depressione. La clinica A tratta soprattutto casi lievi, la clinica B casi gravi.
Dati:
# Clinica A (casi lievi)
n_A_trattati <- 90
n_A_guariti_trattati <- 81 # 90% successo
n_A_controllo <- 10
n_A_guariti_controllo <- 9 # 90% successo
# Clinica B (casi gravi)
n_B_trattati <- 10
n_B_guariti_trattati <- 2 # 20% successo
n_B_controllo <- 90
n_B_guariti_controllo <- 27 # 30% successo
# Proporzioni per clinica
prop_A_trattati <- n_A_guariti_trattati / n_A_trattati
prop_A_controllo <- n_A_guariti_controllo / n_A_controllo
prop_B_trattati <- n_B_guariti_trattati / n_B_trattati
prop_B_controllo <- n_B_guariti_controllo / n_B_controllo
# Aggregato (senza distinguere clinica)
n_tot_trattati <- n_A_trattati + n_B_trattati
n_tot_guariti_trattati <- n_A_guariti_trattati + n_B_guariti_trattati
n_tot_controllo <- n_A_controllo + n_B_controllo
n_tot_guariti_controllo <- n_A_guariti_controllo + n_B_guariti_controllo
prop_tot_trattati <- n_tot_guariti_trattati / n_tot_trattati
prop_tot_controllo <- n_tot_guariti_controllo / n_tot_controllo#> === PARADOSSO DI SIMPSON ===
#> Clinica A (casi lievi):
#> Trattati: 0.9 → 81 / 90
#> Controllo: 0.9 → 9 / 10
#> → Efficacia uguale o leggermente migliore nel gruppo trattamento
#> Clinica B (casi gravi):
#> Trattati: 0.2 → 2 / 10
#> Controllo: 0.3 → 27 / 90
#> → Trattamento migliore anche qui
#> AGGREGATO (A + B):
#> Trattati: 0.83 → 83 / 100
#> Controllo: 0.36 → 36 / 100
#> → NELL'AGGREGATO: sembra che il trattamento funzioni PEGGIO!
#> Spiegazione: la clinica B (casi gravi) contribuisce molto al gruppo trattato,
#> mentre la clinica A (casi lievi) contribuisce molto al gruppo di controllo.
#> Il mix diseguale dei casi (variabile confondente) inverte la relazione osservata.Visualizzazione
Interpretazione epistemica. Il paradosso di Simpson rivela che la probabilità condizionata corretta non è quella aggregata ma quella stratificata per clinica: \[ P(\text{guarigione} \mid \text{trattamento}, \text{clinica}) \] e non \[ P(\text{guarigione} \mid \text{trattamento}). \]
Quando la distribuzione dei casi (lievi/gravi) è squilibrata tra i gruppi, l’analisi aggregata può portare a una conclusione errata: pur essendo benefico in entrambi i sottogruppi, il trattamento appare inefficace nel complesso.
4.7 Applicazioni psicologiche
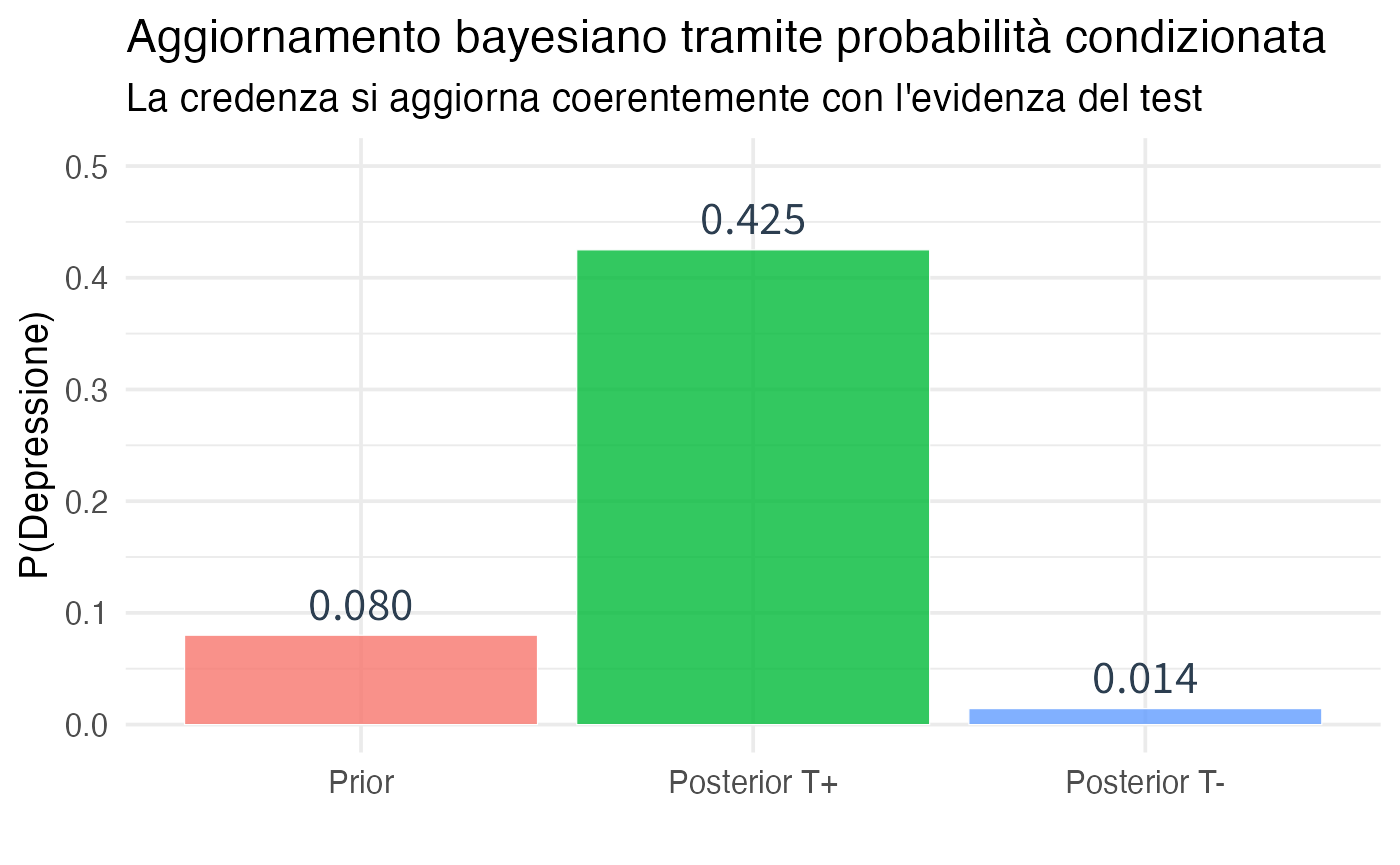
4.7.1 Comorbidità e aggiornamento delle credenze diagnostiche
# Esempio: Depressione e ansia in contesto clinico
P_D <- 0.40
P_A <- 0.35
P_A_given_D <- 0.60 # Alta comorbidità
# Costruire tabella congiunta
P_D_and_A <- P_A_given_D * P_D
P_D_and_notA <- P_D - P_D_and_A
P_notD_and_A <- P_A - P_D_and_A
P_notD_and_notA <- 1 - (P_D_and_A + P_D_and_notA + P_notD_and_A)
tab_comorbid <- matrix(
c(P_D_and_A, P_D_and_notA, P_notD_and_A, P_notD_and_notA),
nrow = 2, byrow = TRUE,
dimnames = list(Depressione = c("D", "D^c"), Ansia = c("A", "A^c"))
)
# Probabilità condizionate
P_D_given_A <- P_D_and_A / P_A
P_D_given_notA <- P_D_and_notA / (1 - P_A)#> ANALISI DELLA COMORBIDITÀ E AGGIORNAMENTO DIAGNOSTICO
#> =====================================================
#> DISTRIBUZIONE A PRIORI (basata su prevalenze):
#> P(Depressione) = 0.4
#> P(Ansia) = 0.35
#> P(Ansia | Depressione) = 0.6 (comorbidità elevata)
#> AGGIORNAMENTO DOPO OSSERVAZIONE CLINICA:
#> Dopo aver rilevato sintomi d'ansia:
#> P(Depressione | Ansia) = 0.686
#> → Aumento della credenza: da 0.4 a 0.686 (+ 29 %)
#> Dopo aver escluso sintomi d'ansia:
#> P(Depressione | Ansia^c) = 0.246
#> → Diminuzione della credenza: da 0.4 a 0.246 (- 15 %)Interpretazione clinica: l’alta comorbidità tra depressione e ansia implica che l’osservazione di sintomi ansiosi costituisce un’evidenza rilevante a favore della presenza di depressione, mentre l’assenza di ansia riduce considerevolmente la probabilità di depressione.
4.7.2 Valore diagnostico incrementale di test multipli
# Scenario: Due test per ADHD in valutazione psicodiagnostica
# T1: Questionario per genitori (Conners)
# T2: Osservazione strutturata in classe
P_ADHD <- 0.10
sens_T1 <- 0.80
spec_T1 <- 0.85
sens_T2 <- 0.75
spec_T2 <- 0.90
# Assumiamo indipendenza condizionale dato lo stato ADHD
# Calcolo probabilità dopo primo test
fp1 <- 1 - spec_T1
P_T1pos <- sens_T1 * P_ADHD + fp1 * (1 - P_ADHD)
P_ADHD_given_T1pos <- (sens_T1 * P_ADHD) / P_T1pos
# Calcolo probabilità dopo entrambi i test positivi
P_ADHD_and_T1pos_and_T2pos <- sens_T1 * sens_T2 * P_ADHD
fp2 <- 1 - spec_T2
P_T1pos_and_T2pos <- sens_T1 * sens_T2 * P_ADHD + fp1 * fp2 * (1 - P_ADHD)
P_ADHD_given_both <- P_ADHD_and_T1pos_and_T2pos / P_T1pos_and_T2pos#> VALORE DIAGNOSTICO INCREMENTALE DI TEST MULTIPLI
#> ================================================
#> CONTESTO: Valutazione psicodiagnostica per ADHD
#> Prevalenza stimata: P(ADHD) = 0.1
#> PROGRESSIONE DELL'AGGIORNAMENTO DIAGNOSTICO:
#> Stato iniziale: P(ADHD) = 0.1
#> Dopo questionario genitori positivo:
#> P(ADHD | T1+) = 0.372
#> Dopo anche osservazione in classe positiva:
#> P(ADHD | T1+, T2+) = 0.816
#> ANALISI DELL'INCREMENTO INFORMATIVO:
#> Incremento dopo primo test: + 27.2 %
#> Incremento dopo secondo test: + 44.4 %
#> Incremento totale: + 71.6 %
#> CONCLUSIONE CLINICA: L'integrazione sequenziale di test multipli con caratteristiche
#> psicometriche complementari produce un accumulo di evidenza diagnostica.Implicazioni per la pratica clinica: l’approccio bayesiano sequenziale giustifica l’uso di batterie di test multiple, dimostrando come ogni strumento contribuisca in modo incrementale alla precisione diagnostica, aspetto particolarmente rilevante in condizioni complesse come, ad esempio, l’ADHD.
Riflessioni conclusive
La probabilità condizionata rappresenta il meccanismo fondamentale attraverso il quale le credenze bayesiane si aggiornano in modo coerente alla luce di nuove informazioni. In questo capitolo abbiamo esplorato le dimensioni essenziali di questo concetto.
La definizione epistemica di \(P(A \mid B)\) quantifica la nostra credenza in \(A\) dopo aver appreso l’informazione \(B\), realizzandosi attraverso un processo di riduzione e rinormalizzazione dello spazio epistemico. Il concetto di indipendenza caratterizza l’assenza di informazione reciproca tra eventi: quando due eventi sono indipendenti, la conoscenza di uno non modifica le nostre credenze riguardo all’altro.
Il teorema del prodotto fornisce il metodo naturale per costruire probabilità congiunte a partire da probabilità condizionate sequenziali, mentre la legge della probabilità totale costituisce uno strumento essenziale per calcolare le probabilità marginali mediante medie ponderate delle probabilità condizionate. Il paradosso di Simpson illustra drammaticamente l’importanza di condizionare sulle variabili appropriate, mostrando come l’aggregazione ingenua dei dati possa invertire artificialmente relazioni genuine.
Nelle applicazioni cliniche, che vanno dai test diagnostici all’analisi della comorbilità, dalla valutazione del valore incrementale di test multipli all’interpretazione dei pattern sintomatologici, il ragionamento condizionato si rivela indispensabile per una pratica evidence-based.
La probabilità condizionata non è solo una formula tecnica, ma rappresenta il nucleo concettuale del ragionamento bayesiano. Nel prossimo capitolo, il teorema di Bayes emergerà come un caso speciale della probabilità condizionata che formalizza l’inversione probabilistica, ovvero il passaggio da \(P(\text{Evidenza} \mid \text{Ipotesi})\) a \(P(\text{Ipotesi} \mid \text{Evidenza})\).
Ogni volta che utilizziamo espressioni come “dato che…”, “sapendo che…”, “alla luce di…”, stiamo implicitamente applicando il principio della probabilità condizionata per aggiornare le nostre credenze in modo logicamente coerente e matematicamente rigoroso.