2  Modelli probabilistici

Introduzione

Dopo aver esaminato il significato filosofico della probabilità nel Capitolo 1, questo capitolo ne sviluppa una trattazione più formale, creando un collegamento tra la riflessione teorica e gli strumenti operativi. Partendo dalla definizione di esperimento casuale – come il lancio di una moneta o la somministrazione di un test psicologico – costruiremo un framework matematico per analizzare e quantificare le proprietà di tali esperimenti. In particolare, approfondiremo i concetti di spazio campionario, eventi e proprietà della probabilità, fornendo le basi per un’interpretazione rigorosa dei fenomeni complessi in psicologia e nelle scienze sociali.

Panoramica del capitolo

  • Nozioni di spazio campionario, eventi e operazioni su eventi.
  • Definizione di probabilità.
  • Spazi discreti o continui.
  • Teorema della somma.
here::here("code", "_common.R") |>
  source()

# Load packages
if (!requireNamespace("pacman")) install.packages("pacman")
pacman::p_load(readr, VennDiagram)

Prima di esaminare in maniera più formale le basi della teoria della probabilità, consideriamo un classico problema della teoria della probabilità:

“Quante persone servono in una stanza perché ci sia almeno il 50% di probabilità che due condividano lo stesso compleanno?”

Questo problema, noto come problema dei compleanni, fu introdotto dal matematico Richard von Mises nel 1932. La sua soluzione sfida l’intuizione e rivela quanto le probabilità combinatorie possano essere ingannevoli.

Rispondi alle seguenti domande.

  1. Con quante persone pensi si superi il 50% di probabilità? (23? 100? 180?)
  2. Con 30 persone, quale probabilità stimi? (10%? 50%? 70%?)

Scrivi le tue risposte su un foglietto senza condividere con i compagni.

Per svolgere un esercizio in classe, compila il seguente modulo su Google Forms.

2.1 Esperimenti casuali

Il concetto fondamentale della probabilità è l’esperimento casuale, ovvero un procedimento il cui esito non può essere previsto con certezza, ma che può essere analizzato quantitativamente. Alcuni esempi di esperimenti casuali includono: lanciare un dado e osservare il numero ottenuto sulla faccia superiore; estrarre una carta a caso da un mazzo e registrarne il seme e il valore; misurare il livello di stress percepito da un gruppo di individui in un determinato contesto, come durante un esame o un evento stressante; contare il numero di risposte corrette fornite dai partecipanti a un test di memoria entro un tempo prestabilito; eccetera.

L’analisi probabilistica ha lo scopo di comprendere il comportamento di esperimenti casuali mediante la costruzione di modelli matematici. Una volta formalizzato matematicamente un esperimento casuale, è possibile calcolare grandezze di interesse, quali probabilità e valori attesi. Tali modelli possono essere implementati su calcolatore per simulare l’esperimento e analizzarne i risultati. Inoltre, la modellizzazione matematica degli esperimenti casuali costituisce il fondamento della statistica, disciplina che consente di confrontare vari modelli e di individuare quello più adeguato ai dati osservati.

2.1.1 Il lancio di una moneta

Uno degli esperimenti casuali più semplici e fondamentali è il lancio ripetuto di una moneta. Questo esperimento elementare permette di illustrare molti concetti chiave della teoria della probabilità. Per studiarne il comportamento, possiamo simularlo al computer utilizzando il linguaggio R.

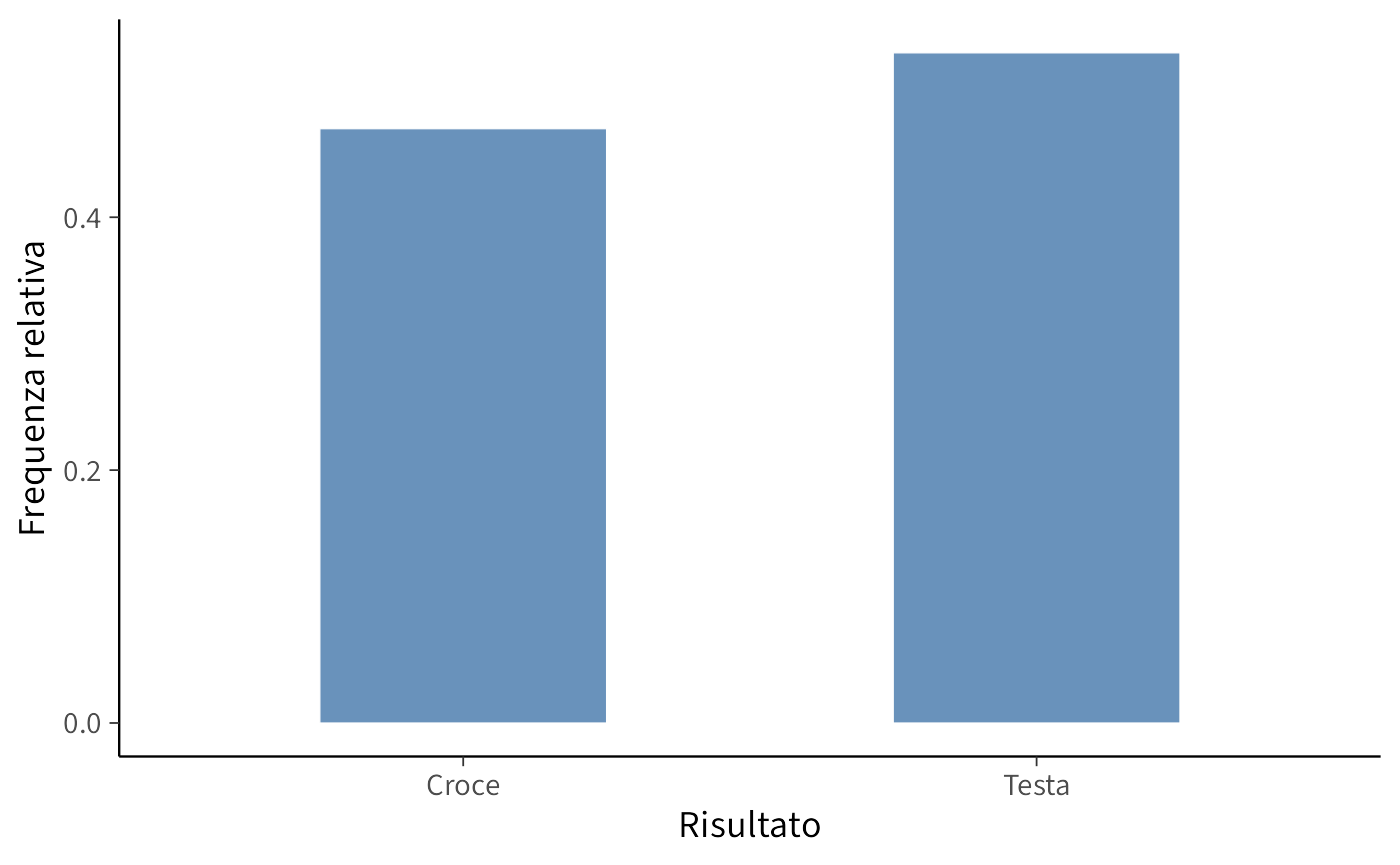
Di seguito, uno script in R simula 100 lanci di una moneta equa (con probabilità uguali di ottenere “testa” o “croce”) e rappresenta graficamente la distribuzione dei risultati mediante un diagramma a barre.

set.seed(123) # Imposta il seed per garantire la riproducibilità
x <- runif(100) < 0.5 # Genera 100 numeri casuali e verifica se sono minori di 0.5
x
#>   [1]  TRUE FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE FALSE  TRUE FALSE  TRUE
#>  [13] FALSE FALSE  TRUE FALSE  TRUE  TRUE  TRUE FALSE FALSE FALSE FALSE FALSE
#>  [25] FALSE FALSE FALSE FALSE  TRUE  TRUE FALSE FALSE FALSE FALSE  TRUE  TRUE
#>  [37] FALSE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE  TRUE
#>  [49]  TRUE FALSE  TRUE  TRUE FALSE  TRUE FALSE  TRUE  TRUE FALSE FALSE  TRUE
#>  [61] FALSE  TRUE  TRUE  TRUE FALSE  TRUE FALSE FALSE FALSE  TRUE FALSE FALSE
#>  [73] FALSE  TRUE  TRUE  TRUE  TRUE FALSE  TRUE  TRUE  TRUE FALSE  TRUE FALSE
#>  [85]  TRUE  TRUE FALSE FALSE FALSE  TRUE  TRUE FALSE  TRUE FALSE  TRUE  TRUE
#>  [97] FALSE  TRUE  TRUE FALSE

Nel codice, la funzione runif genera 100 numeri casuali distribuiti uniformemente nell’intervallo [0, 1]. Confrontando ciascun numero con 0.5, si ottiene un vettore logico che rappresenta il risultato di ogni lancio: Testa (TRUE) o Croce (FALSE).

t <- 1:100 # Sequenza degli indici dei lanci

# Creazione del dataframe per ggplot2
dat <- tibble(
  Lancio = t,
  Risultato = ifelse(x, "Testa", "Croce")
)
head(dat)
#> # A tibble: 6 × 2
#>   Lancio Risultato
#>    <int> <chr>    
#> 1      1 Testa    
#> 2      2 Croce    
#> 3      3 Testa    
#> 4      4 Croce    
#> 5      5 Croce    
#> 6      6 Testa

Il grafico a barre mostra la distribuzione osservata degli esiti.

# Creazione del grafico a barre della distribuzione dei risultati
dat |>
  ggplot(aes(x = Risultato)) +
  geom_bar(aes(y = after_stat(prop), group = 1), width = 0.5) +
  labs(
    x = "Risultato",
    y = "Frequenza relativa"
  )

Un aspetto rilevante di questo esperimento è l’andamento della proporzione osservata di esiti “Testa” in funzione del numero di lanci. Il grafico seguente illustra l’andamento della media cumulativa degli esiti “Testa”, che, in accordo con la legge dei grandi numeri, dovrebbe convergere al valore teorico di 0.5.

y <- cumsum(x) / t # Calcola la media cumulativa delle Teste

# Creazione del dataframe per il grafico della media mobile
data_mean <- tibble(
  Lancio = t, 
  Media_Testa = y
)

# Creazione del grafico della media cumulativa
data_mean |>
  ggplot(
    aes(x = Lancio, y = Media_Testa)
  ) +
  geom_line(linewidth = 1.5) +
  geom_hline(yintercept = 0.5, linetype = "dashed", color = "red") +
  labs(
    x = "Numero di lanci",
    y = "Frequenza cumulativa di Teste"
  )

La media cumulata (o cumulativa) è una media che viene aggiornata incrementalmente ogni volta che un nuovo dato si aggiunge alla serie. Mostra l’evoluzione del valor medio man mano che aumentano le osservazioni.

Calcolo:

Ad ogni passo \(n\), la media cumulata \(M_n\) è data da:

\[ M_n = \frac{\sum_{i=1}^{n} x_i}{n} \]

dove \(x_i\) è il dato all’\(i\)-esimo passo.

Esempio:

Voti di uno studente: 7, 6, 8

  • Dopo 1 verifica: \(M_1 = 7\)
  • Dopo 2 verifiche: \(M_2 = \frac{7 + 6}{2} = 6{,}5\)
  • Dopo 3 verifiche: \(M_3 = \frac{7 + 6 + 8}{3} = 7\)

Utilizzi:

  • analisi di andamenti nel tempo (es.: convergenza di frequenze empiriche);
  • livellamento di fluttuazioni casuali;
  • valutazione di prestazioni cumulative (es.: miglioramento progressivo).

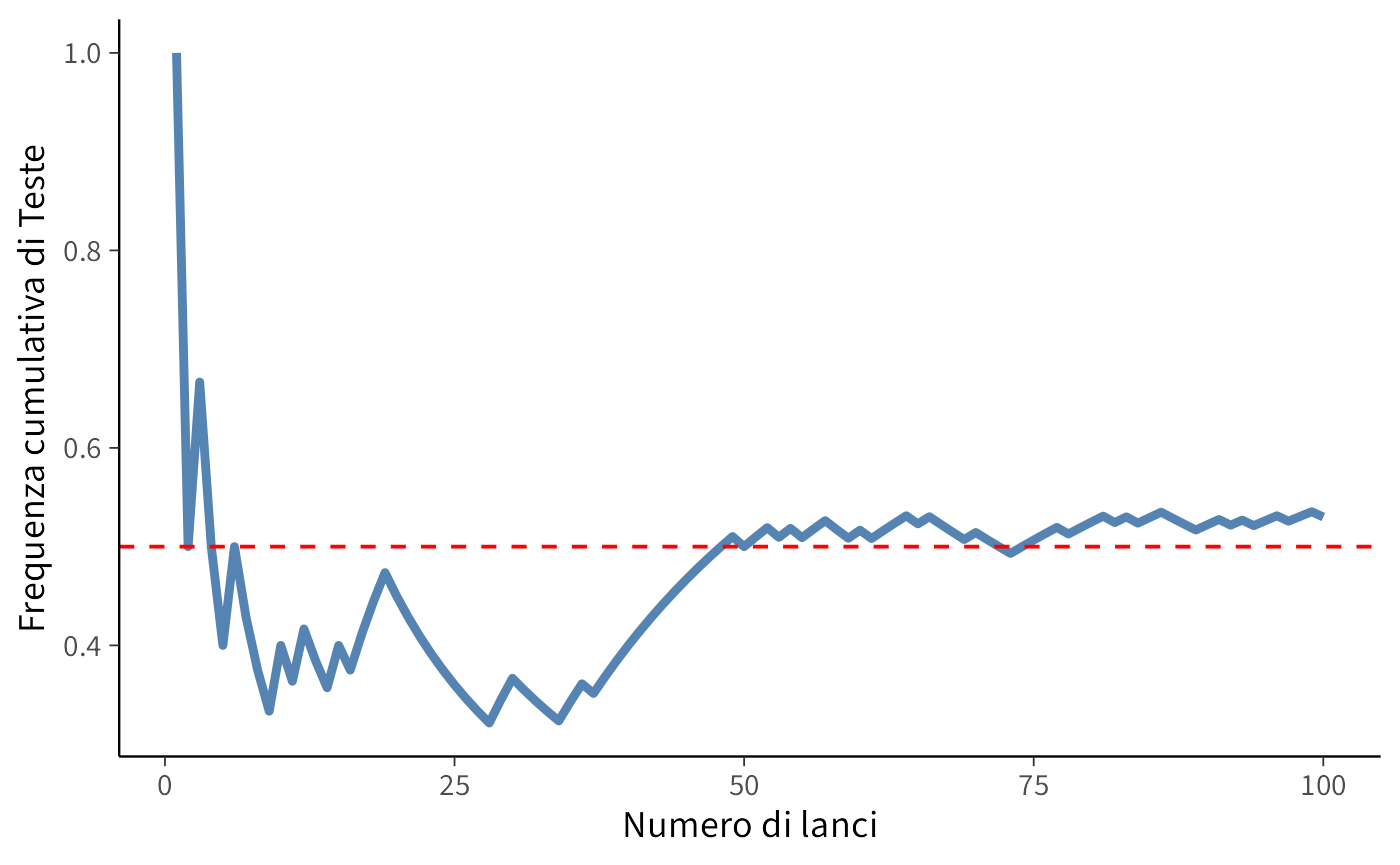
Il grafico mostra come la media delle Teste oscilla inizialmente a causa della variabilità intrinseca dell’esperimento, ma tende progressivamente a stabilizzarsi intorno a 0.5. Questo fenomeno è un esempio della legge dei grandi numeri, secondo cui, ripetendo un esperimento casuale un numero sempre maggiore di volte, la frequenza relativa di un evento si avvicina alla sua probabilità teorica.

2.1.2 Domande di interesse

L’esperimento casuale del lancio di una moneta porta a numerose domande, tra cui:

  • Qual è la probabilità di ottenere un certo numero \(x\) di teste in 100 lanci?
  • Qual è il numero atteso di teste in un esperimento di 100 lanci?

Dal punto di vista statistico, quando osserviamo i risultati di un esperimento reale (ad esempio, 100 lanci di una moneta), possiamo anche porci domande come:

  • La moneta è davvero equa o è sbilanciata?
  • Qual è il miglior metodo per stimare la probabilità \(p\) di ottenere “testa” dalla sequenza osservata di lanci?
  • Quanto è precisa la stima ottenuta e con quale livello di incertezza?

Questi interrogativi costituiscono la base della statistica inferenziale, che permette di testare ipotesi sulla probabilità di un evento e stimare parametri sconosciuti sulla base di dati osservati.

2.1.3 Modellizzazione

La descrizione matematica di un esperimento casuale si basa su tre elementi fondamentali:

  1. Lo spazio campionario: rappresenta l’insieme di tutti i possibili esiti dell’esperimento. Nel caso di esperimenti semplici, lo spazio campionario è immediato da individuare, mentre in situazioni più complesse è necessario applicare i principi del calcolo combinatorio.

  2. Gli eventi: sono sottoinsiemi dello spazio campionario e rappresentano gli esiti di interesse. Per analizzare e manipolare gli eventi, utilizziamo gli strumenti della teoria degli insiemi.

  3. La probabilità: assegna un valore numerico a ciascun evento, indicando la sua probabilità di verificarsi. L’assegnazione delle probabilità avviene secondo gli assiomi di Kolmogorov.

Nei paragrafi seguenti, analizzeremo ciascuna di queste componenti in dettaglio.

2.2 Spazio campionario

Anche se non è possibile prevedere con esattezza l’esito di un singolo esperimento casuale, è comunque possibile definire tutti i risultati che potrebbero verificarsi. L’insieme completo di questi esiti possibili si chiama “spazio campionario”.

Definizione 2.1 Lo spazio campionario \(\Omega\) di un esperimento casuale è l’insieme di tutti i possibili esiti dell’esperimento.

2.2.1 Esempi di spazi campionari

Consideriamo lo spazio campionario di alcuni esperimenti casuali.

  1. Lancio di due dadi consecutivi: \[ \Omega = \{(1,1), (1,2), \dots, (6,6)\}. \]

  2. Tempo di reazione a uno stimolo visivo: \[\Omega = \mathbb{R}^+,\] ovvero l’insieme dei numeri reali positivi.

  3. Numero di errori in un test di memoria a breve termine: \[\Omega = \{0, 1, 2, \dots\}.\]

  4. Misurazione delle altezze di dieci persone: \[\Omega = \{(x_1, \dots, x_{10}) : x_i \ge 0, \; i=1,\dots,10\} \subset \mathbb{R}^{10}.\]

2.3 Eventi

Solitamente, però, non siamo interessati a un singolo esito, ma a un insieme di essi. Un evento è un sottoinsieme dello spazio campionario a cui possiamo assegnare una probabilità.

Definizione 2.2 Un evento è un sottoinsieme \(A \subseteq \Omega\) al quale viene assegnata una probabilità. Gli eventi sono indicati con lettere maiuscole: \(A, B, C, \dots\). Diciamo che l’evento \(A\) si verifica se l’esito dell’esperimento appartiene a \(A\).

2.3.1 Esempi di eventi

Consideriamo alcuni possibili eventi definiti sugli spazi campionari descritti sopra.

  1. Lancio di due dadi consecutivi.
    Evento: “La somma dei due dadi è uguale a 7”
    \[ A = \{(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)\}. \]

  2. Tempo di reazione a uno stimolo visivo.
    Evento: “Il tempo di reazione è inferiore a 2 secondi”
    \[ A = [0, 2). \]

  3. Numero di errori in un test di memoria a breve termine.
    Evento: “Il numero di errori è al massimo 3”
    \[ A = \{0, 1, 2, 3\}. \]

  4. Misurazione delle altezze di dieci persone.
    Evento: “Almeno due persone hanno un’altezza superiore a 180 cm”
    \[ A = \{(x_1, \dots, x_{10}) : \text{almeno due } x_i > 180\}. \]

Questi esempi mostrano come gli eventi possano essere definiti in modo diverso a seconda della natura dello spazio campionario e del contesto di interesse.

Supponiamo di lanciare una moneta tre volte e di annotare se esce Testa (\(H\)) o Croce (\(T\)) in ogni lancio. Lo spazio campionario è:

\[ \Omega = \{HHH, HHT, HTH, HTT, THH, THT, TTH, TTT\}, \]

dove, ad esempio, \(HTH\) indica che il primo lancio dà Testa, il secondo Croce e il terzo Testa.

Un’alternativa è rappresentare lo spazio campionario come l’insieme dei vettori binari di lunghezza 3, \(\{0,1\}^3\), dove Testa (\(H\)) corrisponde a 1 e Croce (\(T\)) a 0.

L’evento \(A\) “il terzo lancio è Testa” si esprime come:

\[ A = \{HHH, HTH, THH, TTH\}. \]

2.4 Operazioni sugli eventi

Poiché gli eventi sono definiti come insiemi, possiamo applicare loro le classiche operazioni insiemistiche.

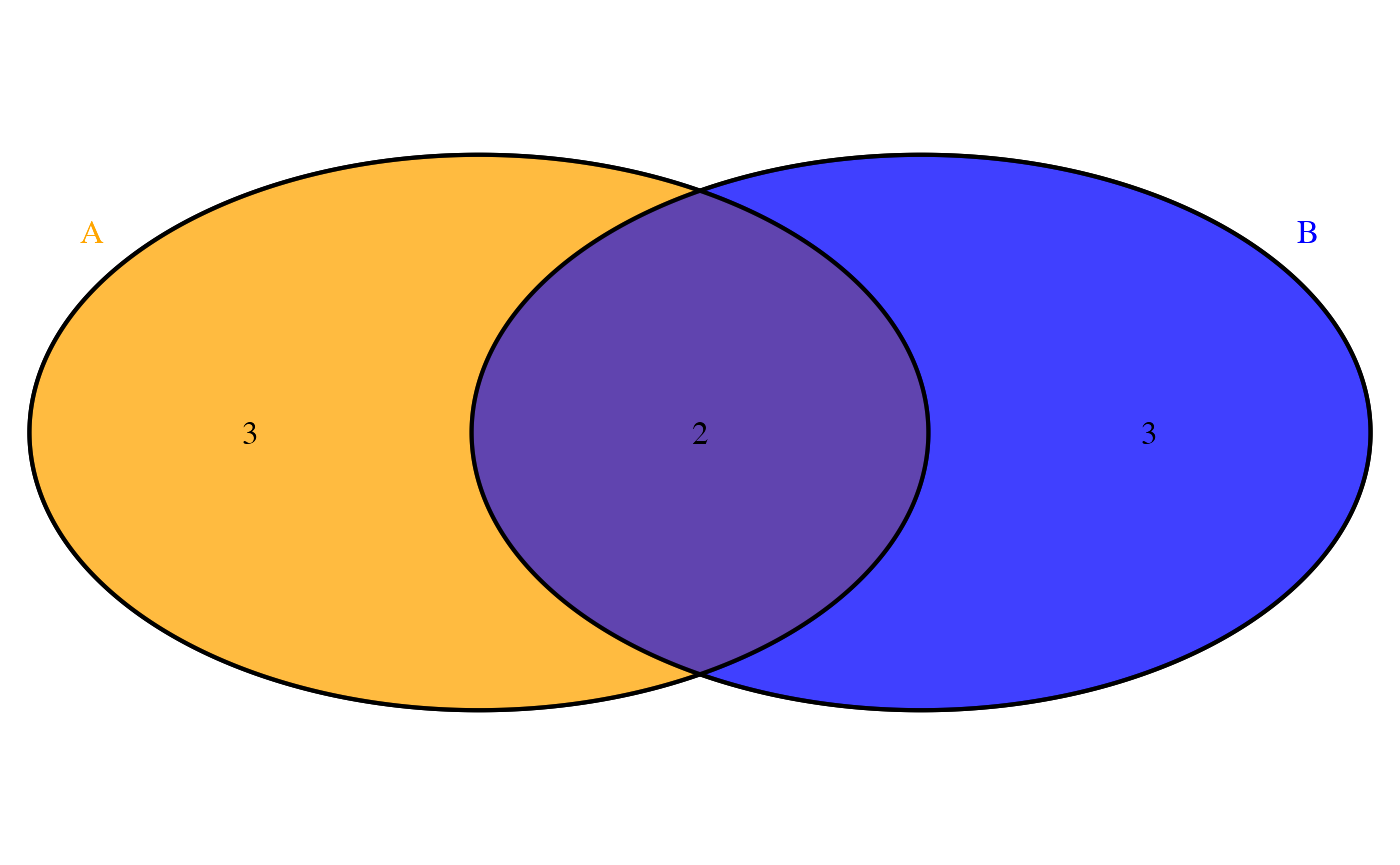
Unione (\(\cup\)). L’unione di due eventi \(A\) e \(B\) è l’insieme di tutti gli esiti che appartengono almeno a uno dei due eventi: \[ A \cup B = \{\omega \in \Omega : \omega \in A \text{ oppure } \omega \in B\}. \]

Intersezione (\(\cap\)). L’intersezione di due eventi è l’insieme degli esiti comuni: \[ A \cap B = \{\omega \in \Omega : \omega \in A \text{ e } \omega \in B\}. \]

Complemento (\(A^c\)). Il complemento di un evento \(A\) è l’insieme di tutti gli esiti che non appartengono ad \(A\): \[ A^c = \{\omega \in \Omega : \omega \notin A\}. \]

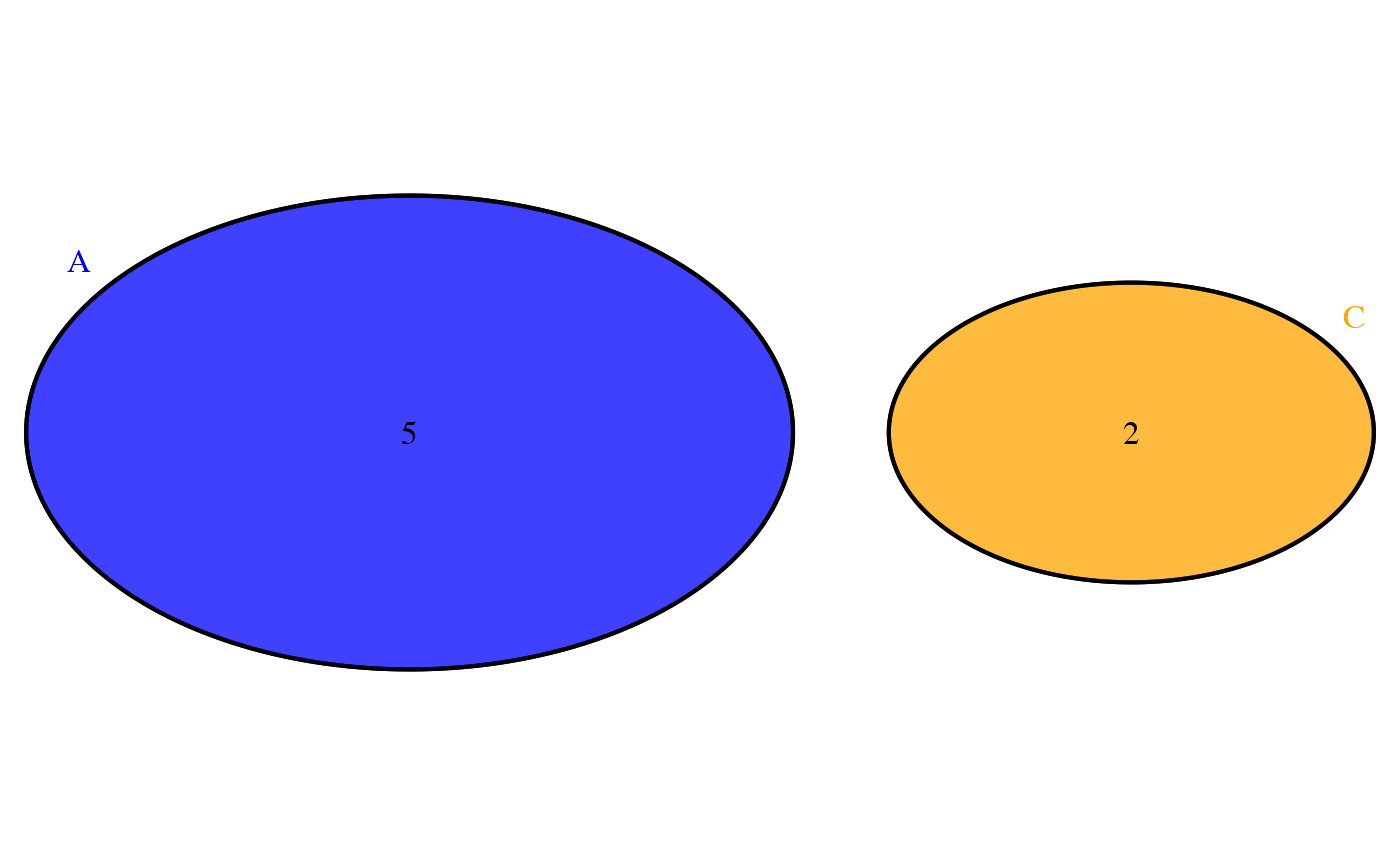
Eventi mutuamente esclusivi. Due eventi sono mutuamente esclusivi se non hanno esiti in comune, ovvero: \[ A \cap B = \emptyset. \]

# Universo
U <- 1:10  

# Definizione degli insiemi A e B
A <- c(1, 2, 3, 4, 5)
B <- c(4, 5, 6, 7, 8)

# Calcolare l'unione, l'intersezione e il complemento relativo a un universo U
union_AB <- union(A, B)
intersect_AB <- intersect(A, B)
complement_A <- setdiff(U, A)
complement_B <- setdiff(U, B)

# Visualizzazione testuale
cat("Unione A ∪ B:", union_AB, "\n")
#> Unione A ∪ B: 1 2 3 4 5 6 7 8
cat("Intersezione A ∩ B:", intersect_AB, "\n")
#> Intersezione A ∩ B: 4 5
cat("Complemento di A:", complement_A, "\n")
#> Complemento di A: 6 7 8 9 10
cat("Complemento di B:", complement_B, "\n")
#> Complemento di B: 1 2 3 9 10
# Visualizzazione con diagrammi di Venn
venn.plot <- draw.pairwise.venn(
  area1 = length(A),
  area2 = length(B),
  cross.area = length(intersect(A, B)),  # Corretto: usa intersect() invece di intersect_AB
  category = c("A", "B"),
  fill = c("orange", "blue"),
  alpha = 0.5,
  cat.col = c("orange", "blue")  # Corretto: allineato con i colori di fill
)

# Visualizza il diagramma
grid.draw(venn.plot)

# Esempio di eventi mutualmente esclusivi
C <- c(9, 10)  # Insieme disgiunto da A e B
intersect_AC <- intersect(A, C)  # Deve essere vuoto

cat("Intersezione A ∩ C (eventi mutualmente esclusivi):", intersect_AC, "\n")
#> Intersezione A ∩ C (eventi mutualmente esclusivi):
# Visualizzazione di eventi mutualmente esclusivi
venn.plot2 <- draw.pairwise.venn(
  area1 = length(A),
  area2 = length(C),
  cross.area = 0,  # Nessuna intersezione
  category = c("A", "C"),
  fill = c("blue", "orange"),
  alpha = 0.5,
  cat.col = c("blue", "orange")
)
grid.draw(venn.plot2)

2.4.1 Proprietà fondamentali delle operazioni su eventi

  • Idempotenza: \[ A \cup A = A, \quad A \cap A = A. \]

  • Leggi di De Morgan: \[ (A \cup B)^c = A^c \cap B^c, \quad (A \cap B)^c = A^c \cup B^c. \]

  • Unione e Intersezione con l’insieme vuoto: \[ A \cup \emptyset = A, \quad A \cap \emptyset = \emptyset. \]

  • Unione e Intersezione con lo spazio campionario: \[ A \cup \Omega = \Omega, \quad A \cap \Omega = A. \]

Queste operazioni forniscono le basi per costruire e manipolare eventi in contesti probabilistici, consentendo di calcolare le probabilità e di prendere decisioni basate sull’analisi degli esiti possibili.

Per gli insiemi definiti nell’esempio precedente, possiamo verificare la prima legge di De Morgan in R confrontando il complemento dell’unione con l’intersezione dei complementi:

  • complemento dell’unione: \((A \cup B)^c\),
  • intersezione dei complementi: \(A^c \cap B^c\).

Eseguiamo i calcoli in R:

# Complemento dell'unione: (A ∪ B)^c
setdiff(U, union(A, B))
#> [1]  9 10
# Intersezione dei complementi: A^c ∩ B^c
intersect(setdiff(U, A), setdiff(U, B))
#> [1]  9 10

Secondo la legge di De Morgan, i due risultati devono coincidere.

Consideriamo l’esperimento del lancio di due dadi. Lo spazio campionario \(\Omega\) è definito dall’insieme di tutte le possibili coppie di risultati:

\[ \Omega = \{(i,j) \mid i,j \in \{1,2,3,4,5,6\}\}, \]

per un totale di \(6^2 = 36\) esiti equiprobabili.

Sia \(A\) l’evento “la somma dei due dadi è almeno 10”. Gli esiti favorevoli sono quelli con somma pari a 10, 11 o 12:

\[ A = \{(4,6), (5,5), (5,6), (6,4), (6,5), (6,6)\}. \]

In R, è possibile generare \(\Omega\) in modo algoritmico e identificare \(A\) come segue:

# Generazione dello spazio campionario
dado <- 1:6
Omega <- expand.grid(Dado1 = dado, Dado2 = dado)

# Aggiunta della colonna Somma
Omega$Somma <- Omega$Dado1 + Omega$Dado2

# Estrazione dell'evento A: somma >= 10
A <- subset(Omega, Somma >= 10)

Il risultato è un dataframe contenente le sei combinazioni favorevoli:

A
#>    Dado1 Dado2 Somma
#> 24     6     4    10
#> 29     5     5    10
#> 30     6     5    11
#> 34     4     6    10
#> 35     5     6    11
#> 36     6     6    12

Questo approccio consente di rappresentare formalmente e operativamente sia lo spazio campionario che l’evento di interesse.

Consideriamo l’esperimento del lancio ripetuto di una moneta per tre volte, in cui ogni esito è rappresentato da una sequenza di “testa” (H) o “croce” (T). Lo spazio campionario \(\Omega\) comprende tutte le \(2^3 = 8\) possibili combinazioni:

\[ \Omega = \{ \text{HHH}, \text{HHT}, \text{HTH}, \text{HTT}, \text{THH}, \text{THT}, \text{TTH}, \text{TTT} \}. \]

Sia \(A\) l’evento “il terzo lancio risulta testa (H)”. Gli elementi di \(A\) sono tutte e sole le sequenze il cui terzo carattere è “H”.

In R, è possibile rappresentare \(\Omega\) e definire \(A\) nel modo seguente:

# Definizione dello spazio campionario
omega <- c("HHH", "HHT", "HTH", "HTT", "THH", "THT", "TTH", "TTT")

# Identificazione delle sequenze con terzo carattere "H"
A <- omega[substr(omega, 3, 3) == "H"]

Il vettore risultante \(A\) conterrà gli elementi:

A
#> [1] "HHH" "HTH" "THH" "TTH"

Questo approccio sfrutta l’indicizzazione logica e la funzione substr() per estrarre efficientemente gli esiti che soddisfano la condizione desiderata, dimostrando come rappresentare e manipolare eventi in contesti probabilistici mediante operazioni vettoriali in R.

Consideriamo l’esperimento del lancio di due dadi. Lo spazio campionario \(\Omega\) è dato dall’insieme di tutte le possibili coppie ordinate di risultati:

\[ \Omega = \{(i,j) \mid i,j \in \{1,2,3,4,5,6\}\}, \] per un totale di \(36\) esiti equiprobabili.

Definiamo due eventi:

  1. Evento A: “Il primo dado mostra un 6”

    \[ A = \{(6,j) \mid j \in \{1,2,3,4,5,6\}\} \]

  2. Evento B: “Il secondo dado mostra un 6”

    \[ B = \{(i,6) \mid i \in \{1,2,3,4,5,6\}\} \]

L’intersezione dei due eventi corrisponde al caso in cui entrambi i dadi mostrano un 6:

\[ A \cap B = \{(6,6)\}. \]

2.4.2 Implementazione in R

# Generazione dello spazio campionario
dado <- 1:6
Omega <- expand.grid(Dado1 = dado, Dado2 = dado)

# Definizione degli eventi
A <- subset(Omega, Dado1 == 6)  # Primo dado = 6
B <- subset(Omega, Dado2 == 6)  # Secondo dado = 6

# Intersezione corretta (due modi equivalenti)
A_intersezione_B <- merge(A, B)                     # con merge
# A_intersezione_B <- subset(Omega, Dado1 == 6 & Dado2 == 6)  # con subset logico

# Dimensioni degli insiemi
n_tot <- nrow(Omega)      # Numero totale di esiti
n_A   <- nrow(A)          # Numero di esiti in A
n_B   <- nrow(B)          # Numero di esiti in B
n_AB  <- nrow(A_intersezione_B)  # Numero di esiti in A ∩ B

# Probabilità
p_A  <- n_A  / n_tot
p_B  <- n_B  / n_tot
p_AB <- n_AB / n_tot

list(
  Prob_A = p_A,
  Prob_B = p_B,
  Prob_A_intersezione_B = p_AB
)
#> $Prob_A
#> [1] 0.167
#> 
#> $Prob_B
#> [1] 0.167
#> 
#> $Prob_A_intersezione_B
#> [1] 0.0278

2.4.3 Interpretazione

  • \(P(A) = 1/6 \approx 0.167\): la probabilità che il primo dado mostri un 6.
  • \(P(B) = 1/6 \approx 0.167\): la probabilità che il secondo dado mostri un 6.
  • \(P(A \cap B) = 1/36 \approx 0.028\): la probabilità che entrambi i dadi mostrino un 6.

2.5 Probabilità

Il terzo elemento fondamentale del modello probabilistico è la funzione di probabilità, che quantifica numericamente la possibilità di occorrenza degli eventi.

Definizione 2.3 Una probabilità \(P\) è una funzione \(P: \mathcal{F} \to [0,1]\) definita su una \(\sigma\)-algebra \(\mathcal{F}\) di sottoinsiemi di \(\Omega\)1, che soddisfa i seguenti assiomi di Kolmogorov:

  1. Non-negatività: per ogni evento \(A \in \mathcal{F}\),
    \[ P(A) \geq 0. \]

  2. Normalizzazione: la probabilità dell’evento certo è
    \[ P(\Omega) = 1. \]

  3. Additività numerabile: per ogni successione di eventi \(A_1, A_2, \dots \in \mathcal{F}\) a due a due disgiunti (cioè \(A_i \cap A_j = \emptyset\) per \(i \neq j\)),
    \[ P\left( \bigcup_{i=1}^{\infty} A_i \right) = \sum_{i=1}^{\infty} P(A_i). \]

In altri termini, una misura di probabilità assegna a ogni evento un valore nell’intervallo \([0,1]\), garantendo che l’evento certo abbia probabilità 1 e che la probabilità dell’unione di eventi incompatibili sia uguale alla somma delle loro probabilità. Questi assiomi forniscono le fondamenta formali per una teoria della probabilità coerente e intuitivamente plausibile.

2.5.1 Interpretazione degli assiomi di Kolmogorov

  1. Assioma 1 (Non-negatività e limiti 0–1)
    La probabilità di qualsiasi evento è un numero reale non negativo e non superiore a 1. Un evento con probabilità 0 è considerato praticamente impossibile, mentre un evento con probabilità 1 è certo.
    Esempio: nel lancio di un dado equilibrato a sei facce, l’evento “esce il numero 7” ha probabilità 0, mentre l’evento “esce un numero compreso tra 1 e 6” ha probabilità 1.

  2. Assioma 2 (Evento certo)
    La probabilità dell’intero spazio campionario \(\Omega\) è pari a 1, il che riflette il fatto che in ogni realizzazione dell’esperimento si verifica necessariamente uno degli esiti possibili.
    Esempio: nel lancio di un dado, lo spazio campionario \(\Omega\) è \(\{1,2,3,4,5,6\}\). L’evento “esce un numero appartenente a \(\Omega\)” è certo, quindi \(P(\Omega) = 1\).

  3. Assioma 3 (Additività per eventi incompatibili)
    Se una sequenza di eventi \(A_1, A_2, \dots\) è disgiunta due a due (cioè se \(A_i \cap A_j = \emptyset\) per ogni coppia di indici \(i, j\) con \(i \neq j\)), allora la probabilità della loro unione è uguale alla somma delle probabilità dei singoli eventi. Esempio: nel lancio di un dado, gli eventi “esce 2” e “esce 5” sono incompatibili. Pertanto,
    \[ P(\text{“pari”} \cup \text{“dispari”}) \;=\; P(\text{“pari”}) + P(\text{“dispari”})\,. \]

Questi assiomi garantiscono che la funzione di probabilità sia matematicamente coerente e rispecchi l’intuizione empirica: i valori negativi sono esclusi, la certezza è normalizzata a 1 e il comportamento della probabilità rispetto all’unione di eventi disgiunti è additivo.

2.5.2 Proprietà fondamentali

Dagli assiomi di Kolmogorov derivano alcune proprietà fondamentali che descrivono il comportamento della probabilità in varie situazioni. Le principali sono elencate di seguito.

Teorema 2.1 (Proprietà fondamentali della misura di probabilità) Siano \(A\) e \(B\) due eventi qualsiasi appartenenti a una \(\sigma\)-algebra \(\mathcal{F}\) definita sullo spazio campionario \(\Omega\). Valgono le seguenti proprietà:

  1. Probabilità dell’evento impossibile
    \[ P(\emptyset) = 0. \] L’insieme vuoto, che rappresenta l’assenza di esiti favorevoli, costituisce un evento con probabilità nulla.

  2. Monotonicità della probabilità
    \[ A \subseteq B \quad \Longrightarrow \quad P(A) \leq P(B). \] Se un evento è interamente contenuto in un altro, la sua probabilità non può essere maggiore di quella dell’evento che lo comprende.

  3. Probabilità dell’evento complementare
    \[ P(A^c) = 1 - P(A). \] Poiché \(A\) e il suo complementare \(A^c\) coprono l’intero spazio \(\Omega\), la probabilità di \(A^c\) è la parte “rimanente” fino a 1.

  4. Principio di inclusione-esclusione per due eventi
    \[ P(A \cup B) = P(A) + P(B) - P(A \cap B). \] Per calcolare la probabilità dell’unione di due eventi qualsiasi, si sommano le probabilità di ciascun evento e si sottrae la probabilità della loro intersezione, altrimenti verrebbe conteggiata due volte.

2.6 Spazi discreti e continui

La natura dello spazio campionario determina come definiamo e calcoliamo le probabilità. Distinguiamo i due casi fondamentali: lo spazio campionario discreto

\[ \Omega = \{a_1, a_2, \dots, a_n\} \quad \text{oppure} \quad \Omega = \{a_1, a_2, \dots\} \] e lo spazio campionario continuo

\[ \Omega = \mathbb{R} . \]

2.6.1 Spazi campionari discreti

Definizione:
Uno spazio campionario si dice discreto quando l’insieme dei possibili esiti è finito o numerabile (ovvero, i suoi elementi possono essere posti in corrispondenza biunivoca con i numeri naturali).

Caratteristiche:

  • gli esiti sono isolabili e distinti;
  • la probabilità è completamente determinata dall’assegnazione di pesi non negativi a ciascun esito elementare.

Esempi:

  • lancio di un dado: \(\Omega = \{1, 2, 3, 4, 5, 6\}\) (finito);
  • numero di decadimenti radioattivi in un intervallo temporale: \(\Omega = {0, 1, 2, \dots}\) (numerabile).

Assegnazione della probabilità:

  • A ogni esito \(\omega_i\) viene associato un valore \(p_i \geq 0\), detto probabilità elementare, tale che:
    \[ \sum_{i} p_i = 1. \]
    Questa condizione garantisce la normalizzazione della misura di probabilità.

  • La probabilità di un qualsiasi evento \(A \subseteq \Omega\) è data da:
    \[ P(A) = \sum_{\omega_i \in A} p_i. \]
    In altri termini, \(P(A)\) corrisponde alla somma delle probabilità di tutti gli esiti elementari contenuti in \(A\).

Questa costruzione assicura che la funzione \(P\) soddisfi gli assiomi di Kolmogorov e definisca pertanto una misura di probabilità sullo spazio discreto.

Immaginiamo di lanciare un dado equilibrato a sei facce. Poiché il dado è bilanciato, ogni faccia ha esattamente la stessa probabilità di uscire. Assegniamo quindi a ciascun esito elementare — l’uscita di uno specifico numero da 1 a 6 — una probabilità pari a \(\frac{1}{6}\).

Supponiamo ora di voler determinare la probabilità dell’evento \(A\): “esce un numero pari”. I risultati favorevoli a questo evento sono uscire 2, 4 o 6.

Per calcolare \(P(A)\), sommiamo le probabilità elementari di tutti gli esiti che realizzano l’evento: \[ P(A) = P(\{2\}) + P(\{4\}) + P(\{6\}) = \frac{1}{6} + \frac{1}{6} + \frac{1}{6} = \frac{3}{6} = \frac{1}{2}. \] Dunque, la probabilità che esca un numero pari è \(\frac{1}{2}\), un risultato che conferma la nostra intuizione: metà dei possibili esiti sono numeri pari.

2.6.2 Spazi campionari continui

Definizione:
Uno spazio campionario si dice continuo quando l’insieme dei possibili esiti è non numerabile e forma tipicamente un intervallo o un’unione di intervalli sulla retta reale. In tali spazi, la probabilità associata a singoli punti è infinitesimale e la probabilità viene definita tramite densità.

Caratteristiche:

  • gli esiti non sono isolabili, ma costituiscono un insieme continuo (ad esempio, un intervallo);
  • la probabilità di un singolo punto è zero; ha significato probabilistico solo parlare di probabilità su insiemi di misura non nulla (come intervalli).

Esempi:

  • tempo di attesa per l’arrivo di un autobus: \(\Omega = [0, \infty)\);
  • altezza di un individuo adulto: \(\Omega = [50, 250]\) (in cm, ottenuta con uno strumento infinitamente preciso).

Assegnazione della probabilità:

  • La probabilità è descritta da una funzione di densità di probabilità (PDF) \(f(x) \geq 0\), che deve soddisfare la condizione di normalizzazione:
    \[ \int_{-\infty}^{\infty} f(x)\, dx = 1. \]
    Questa condizione garantisce che la probabilità totale su tutto lo spazio campionario sia unitaria.

  • La probabilità di un evento \(A \subseteq \Omega\) (ad esempio, un intervallo) si calcola integrando la densità su \(A\):
    \[ P(A) = \int_{A} f(x)\, dx. \]
    In particolare, se \(A = [a, b]\), allora:
    \[ P(a \leq X \leq b) = \int_{a}^{b} f(x)\, dx. \]

Questa costruzione garantisce che la funzione \(P\) sia coerente con gli assiomi di Kolmogorov, fornendo una base rigorosa per la modellizzazione probabilistica di fenomeni continui.

2.6.3 Modellizzazione dell’altezza degli uomini adulti

L’altezza degli uomini adulti può essere modellata attraverso una variabile casuale continua \(X\) (espressa in cm), che segue una distribuzione normale con media \(\mu = 170\) cm e deviazione standard \(\sigma = 7\) cm, denotata come:

\[ X \sim \mathcal{N}(170, 7^2). \] La corrispondente funzione di densità di probabilità (PDF) è:

\[ f(x) = \frac{1}{7\sqrt{2\pi}} \exp\left(-\frac{(x - 170)^2}{2 \cdot 49}\right). \]

Evento di interesse:
Si consideri l’evento \(A\): “l’altezza è compresa tra 160 cm e 180 cm”.

Calcolo probabilistico:
La probabilità di \(A\) corrisponde all’area sottesa dalla curva di densità nell’intervallo \([160, 180]\), calcolata come:

\[ P(A) = \int_{160}^{180} \frac{1}{7\sqrt{2\pi}} \exp\left(-\frac{(x - 170)^2}{98}\right) dx. \] Tale integrale, se valutato analiticamente, restituisce un valore pari circa a 0.847, ovvero 84.7%.

Calcolo computazionale in R:
In ambiente R, è possibile ottenere lo stesso risultato sfruttando la funzione di ripartizione (CDF) della distribuzione normale, implementata dalla funzione pnorm():

pnorm(180, mean = 170, sd = 7) - pnorm(160, mean = 170, sd = 7)
#> [1] 0.847

Il risultato conferma che circa l’85% della popolazione maschile adulta rientra in questo intervallo di altezze.

2.6.4 Confronto chiave

Caratteristica Spazio Discreto Spazio Continuo
Esiti Numerabili (es: 1, 2, 3) Non numerabili (es: intervalli)
Probabilità di un singolo punto \(P(\{\omega_i\}) = p_i\) (\(\geq\) 0) \(P(\{x\}) = 0\) (sempre zero)
Strumento matematico Somma \(\sum\) Integrale \(\int\)
Esempi comuni Dadi, monete, conteggi Misure fisiche, tempi, temperature
AvvisoProprietà della PDF
  • Negli spazi continui, la PDF non è una probabilità (può essere > 1), ma la sua area sottesa su un intervallo fornisce la probabilità.
  • Per eventi continui, ha senso solo calcolare probabilità su intervalli (es: \(P(160 \leq X \leq 180)\)).

2.6.5 Dai concetti base alle proprietà fondamentali della probabilità

Abbiamo visto come un esperimento casuale possa essere formalizzato matematicamente attraverso tre elementi chiave:

  • Spazio campionario (\(\Omega\)): l’insieme di tutti i possibili esiti dell’esperimento.
  • Eventi: sottoinsiemi di \(\Omega\) che rappresentano combinazioni di esiti di interesse.
  • Probabilità: una funzione \(P\) che assegna a ogni evento un valore numerico compreso tra 0 e 1, misurandone il grado di verosimiglianza.

A partire da queste definizioni, è possibile derivare proprietà essenziali per il calcolo e l’analisi probabilistica. Queste proprietà permettono di calcolare la probabilità di eventi complessi a partire da eventi elementari e di stabilire relazioni logiche tra di essi.

In questo corso, approfondiremo quattro teoremi fondamentali:

  1. teorema della somma;
  2. teorema del prodotto;
  3. teorema della probabilità totale;
  4. teorema di Bayes.

L’introduzione di operazioni sugli eventi (unione, intersezione, complemento) e delle proprietà della probabilità (teorema della somma, probabilità condizionata, teorema della probabilità totale, …) ci permette di costruire modelli probabilistici più complessi e applicabili a problemi reali.

Qui di seguito, approfondiamo il teorema della somma.

2.7 Teorema della somma

Il teorema della somma (o regola additiva) permette di determinare la probabilità che si verifichi almeno uno tra due eventi \(A\) e \(B\). La sua formulazione dipende dalla relazione tra i due eventi:

Caso 1: eventi mutuamente esclusivi. Se \(A\) e \(B\) non possono verificarsi insieme (ossia \(A \cap B = \emptyset\)), la probabilità dell’unione è data dalla somma delle singole probabilità:

\[ P(A \cup B) = P(A) + P(B). \tag{2.1}\]

Caso 2: eventi non esclusivi. Se \(A\) e \(B\) possono coesistere, è necessario evitare di contare due volte la loro intersezione:

\[ P(A \cup B) = P(A) + P(B) - P(A \cap B). \tag{2.2}\]

Perché questa differenza?
La probabilità è una funzione d’insieme coerente con le operazioni insiemistiche. L’addizione diretta \(P(A) + P(B)\) conteggia due volte gli esiti comuni a \(A\) e \(B\) (rappresentati da \(A \cap B\)). La sottrazione di \(P(A \cap B)\) garantisce che ogni esito sia considerato una sola volta.

Il teorema della somma mette in luce come le operazioni logiche tra eventi (unione e intersezione) si traducano in relazioni algebriche tra le loro probabilità, offrendo uno strumento operativo per la modellazione di scenari reali.

In uno studio sulla salute mentale, supponiamo di avere i seguenti dati relativi a un campione di partecipanti:

  • la probabilità che un individuo soffra di ansia è \(P(A) = 0.30\);
  • la probabilità che un individuo soffra di depressione è \(P(B) = 0.25\);
  • la probabilità che un individuo soffra contemporaneamente di ansia e depressione è \(P(A \cap B) = 0.15\).

Vogliamo calcolare la probabilità che un individuo soffra di almeno uno dei due disturbi (ansia o depressione), ovvero \(P(A \cup B)\).

Utilizziamo la regola della somma per eventi non mutuamente esclusivi:

\[ P(A \cup B) = P(A) + P(B) - P(A \cap B) \]

Svolgiamo questo calcolo in R:

# Definiamo le probabilità
P_A <- 0.30 # Probabilità di soffrire di ansia
P_B <- 0.25 # Probabilità di soffrire di depressione
P_A_intersect_B <- 0.15 # Probabilità di soffrire di entrambi i disturbi

# Applichiamo la formula della regola della somma
P_A_union_B <- P_A + P_B - P_A_intersect_B
P_A_union_B
#> [1] 0.4

Interpretazione: il 40% dei partecipanti soffre di almeno uno tra ansia e depressione. L’intersezione \(P(A \cap B) = 0.15\) è fondamentale, poiché senza sottrarla avremmo contato due volte i soggetti che soffrono contemporaneamente di entrambi i disturbi.

2.8 Probabilità, calcolo combinatorio e simulazioni

In numerosi contesti probabilistici, specialmente in ambito introduttivo, si adotta l’ipotesi di equiprobabilità degli eventi elementari. In tal caso, la probabilità di un evento \(A\) si riduce al rapporto tra il numero di casi favorevoli e il numero di casi possibili:

\[ P(A) = \frac{\#A}{\#\Omega}. \]

In questo contesto, il calcolo combinatorio fornisce gli strumenti formali per elencare in modo efficiente le configurazioni rilevanti. Il procedimento generale prevede:

  1. Identificazione dei casi favorevoli: determinare tutte le configurazioni che realizzano l’evento di interesse.
  2. Conteggio sistematico: calcolare il numero di casi favorevoli e il numero totale di esiti possibili, applicando le tecniche combinatorie appropriate (disposizioni, permutazioni, combinazioni, ecc.).

Estrazione di una pallina da un’urna

Supponiamo di avere un’urna con 10 palline numerate da 1 a 10, da cui estraiamo una sola pallina in modo casuale. Assumendo che ogni pallina abbia la stessa probabilità di essere estratta, calcoliamo la probabilità di estrarre un numero pari.

  • Casi favorevoli: palline con numero pari: \(\{\;2, 4, 6, 8, 10\}\) (5 elementi).
  • Casi possibili: tutte le palline: \(\{\;1, 2, 3, 4, 5, 6, 7, 8, 9, 10\}\) (10 elementi).

La probabilità dell’evento è data dal rapporto tra casi favorevoli e casi possibili:

\[ P(\text{numero pari}) \;=\; \frac{\text{numero di casi favorevoli}}{\text{numero di casi possibili}} \;=\; \frac{5}{10} \;=\; 0.5. \]

Nelle applicazioni più complesse, come il calcolo della probabilità di ottenere una specifica configurazione di carte o la formazione di gruppi con caratteristiche definite a partire da un insieme più ampio, è necessario ricorrere a strumenti combinatoriali avanzati. In particolare, l’uso di permutazioni e combinazioni (si veda la Sezione Appendice E) permette di enumerare in modo efficiente e sistematico sia il numero totale di esiti possibili, sia il numero di quelli favorevoli all’evento di interesse.

2.8.1 Simulazioni Monte Carlo

Uno degli aspetti più impegnativi della probabilità risiede nella complessità di molti problemi che, spesso, non ammettono soluzioni immediate o intuitive. Per affrontarli, è possibile adottare due approcci fondamentali: il primo, di natura analitica, applica i teoremi della teoria della probabilità in modo rigoroso, ma a volte poco intuitivo; il secondo, di tipo computazionale, utilizza la simulazione Monte Carlo che fornisce una soluzione approssimata, ma molto vicina al valore reale, attraverso una procedura accessibile e intuitiva.

Le simulazioni Monte Carlo rientrano nella classe dei metodi stocastici, in contrapposizione a quelli deterministici, e permettono di risolvere in modo approssimato problemi analitici attraverso la generazione casuale di campioni. Tra le tecniche più utilizzate vi sono il campionamento con reinserimento — che consente la selezione ripetuta della stessa unità — e il campionamento senza reinserimento — in cui ogni unità può essere estratta una sola volta. Queste metodologie rappresentano uno strumento potente e flessibile per l’analisi di scenari complessi.

Un esempio classico di applicazione del metodo Monte Carlo è il calcolo delle probabilità nel problema dei compleanni, che esplora la probabilità che, in un gruppo di \(n\) persone, almeno due condividano la stessa data di nascita. Assumendo una distribuzione uniforme dei compleanni su 365 giorni (trascurando gli anni bisestili), il risultato è spesso controintuitivo: con soli 23 individui, la probabilità che si verifichi una coincidenza supera il 50%.

2.8.1.1 Soluzione analitica

Il problema può essere risolto utilizzando il principio delle probabilità complementari. I due eventi

  • tutti i compleanni sono distinti
  • almeno due persone condividono il compleanno

sono mutuamente esclusivi ed esaustivi. Pertanto:

\[ P(\text{almeno un compleanno in comune}) = 1 - P(\text{nessun compleanno in comune}). \]

La probabilità che tutti i compleanni siano diversi è:

\[ \begin{aligned} P(\text{nessun compleanno in comune}) &= \frac{365}{365} \cdot \frac{364}{365} \cdot \frac{363}{365} \cdot \ldots \cdot \frac{365 - n + 1}{365} \\ &= \frac{365!}{(365 - n)! \cdot 365^n}. \end{aligned} \]

Per \(n = 23\):

\[ P(\text{nessun compleanno in comune}) \approx 0.4927, \] \[ P(\text{almeno un compleanno in comune}) \approx 1 - 0.4927 = 0.5073. \]

Il risultato è sorprendente: con 23 persone, la probabilità di una coincidenza supera il 50%.

2.8.1.2 Soluzione con simulazione in R

Per approssimare la probabilità tramite simulazione, generiamo ripetutamente gruppi di \(n\) persone con compleanni casuali e verifichiamo la presenza di duplicati.

# Numero di simulazioni
num_simulazioni <- 10000

# Funzione per simulare il problema del compleanno
simula_compleanno <- function(n) {
  successi <- 0
  for (i in 1:num_simulazioni) {
    compleanni <- sample(1:365, n, replace = TRUE)
    if (any(duplicated(compleanni))) {
      successi <- successi + 1
    }
  }
  return(successi / num_simulazioni)
}

# Calcolo per n da 1 a 50
set.seed(123)
risultati <- sapply(1:50, simula_compleanno)

# Visualizzazione
df <- data.frame(n = 1:50, prob = risultati)
ggplot(df, aes(x = n, y = prob)) +
  geom_line(color = "steelblue") +
  geom_point(color = "steelblue") +
  geom_hline(yintercept = 0.5, color = "darkorange", linetype = "dashed") +
  labs(
    x = "Numero di persone (n)",
    y = "Probabilità stimata"
  )

Risultati attesi:

  • la probabilità stimata supera il 50% per \(n \approx 23\);
  • la curva mostra una crescita rapida per \(n\) piccoli e tende asintoticamente a 1 per \(n\) grandi.

Questo approccio simulativo consente di validare i risultati teorici e di apprezzare visivamente il comportamento probabilistico del sistema.

2.8.1.3 Assunzioni

Il problema dei compleanni discusso in precedenza non solo illustra l’efficacia dell’approccio simulativo nel semplificare la soluzione rispetto all’analisi formale, ma evidenzia anche l’importanza delle assunzioni condivise da entrambi i metodi. In questo caso, l’assunzione fondamentale è che la probabilità di nascita sia uniformemente distribuita tra i 365 giorni dell’anno — un’ipotesi semplificativa che non riflette la reale distribuzione delle nascite, influenzata da fattori stagionali, culturali e sociali.

Questo esempio evidenzia un principio fondamentale della modellazione probabilistica (e scientifica in generale): ogni modello poggia su un insieme di assunzioni che ne definiscono la validità e il campo di applicazione. Una valutazione critica della plausibilità di tali assunzioni è quindi essenziale per determinare se il modello fornisce una rappresentazione significativa del fenomeno in esame.

Riflessioni conclusive

La teoria della probabilità fornisce un quadro rigoroso per descrivere e analizzare fenomeni caratterizzati dall’incertezza. In questo capitolo abbiamo introdotto i concetti fondamentali del calcolo delle probabilità, mostrando come la modellazione matematica degli esperimenti casuali permetta di quantificare e prevedere gli eventi incerti. Abbiamo esplorato strumenti essenziali come la definizione di spazio campionario, la nozione di evento e le regole della probabilità, illustrandone l’utilizzo sia attraverso esempi teorici sia mediante simulazioni computazionali.

Un aspetto cruciale della modellazione probabilistica è il ruolo delle assunzioni su cui si basano i modelli. Ogni modello probabilistico si basa su ipotesi specifiche riguardo alla natura del fenomeno studiato e al modo in cui gli esiti vengono generati. Queste ipotesi non solo determinano la validità del modello, ma anche il tipo di risposte che esso può fornire. Ad esempio, nel problema del compleanno, abbiamo ipotizzato che i compleanni siano distribuiti in modo uniforme nei 365 giorni dell’anno. Sebbene questa assunzione semplifichi notevolmente i calcoli, sappiamo che nella realtà esistono fluttuazioni stagionali delle nascite che possono influenzare le probabilità effettive.

Ciò ci porta a una considerazione più ampia: la probabilità non è solo un insieme di formule, ma uno strumento per rappresentare l’incertezza e prendere decisioni informate. Tuttavia, l’accuratezza di qualsiasi modello probabilistico dipende strettamente dalla plausibilità delle ipotesi adottate. Modelli diversi, basati su ipotesi differenti, possono condurre a risultati diversi e l’interpretazione dei risultati deve sempre tenere conto di queste ipotesi.

In definitiva, lo studio della probabilità non si limita alla manipolazione di formule, ma richiede un’attenta riflessione sulla relazione tra i modelli teorici e i fenomeni reali. Una comprensione critica delle assunzioni su cui si basa un modello è essenziale per applicare correttamente i concetti probabilistici in contesti pratici, sia in ambito scientifico che nelle decisioni di tutti i giorni.

Il 92% delle persone sovrastima il numero necessario per la prima domanda e sottostima la seconda probabilità. Questo problema mostra come l’intuizione umana fallisca con eventi apparentemente “rari”.

  1. La risposta è 23 persone.
  2. La probabilità è \(\sim 0.7\)

Esercizi

Qui di seguito sono presentati una serie di esercizi sbasati sulla Satisfaction with Life Scale (SWLS).

Esercizi sullo Spazio Campionario e Eventi

  1. Definizione dello Spazio Campionario
    Supponiamo che i punteggi della Satisfaction with Life Scale (SWLS) siano numeri interi compresi tra 5 e 35.

    • Qual è lo spazio campionario \(\Omega\) per questo esperimento?
    • Se hai raccolto i dati di 15 studenti, come potresti rappresentare lo spazio campionario con i loro punteggi osservati?

  2. Definizione di un Evento
    Consideriamo l’evento A: “Uno studente ha un punteggio SWLS superiore a 25”.

    • Esprimi l’evento A come un sottoinsieme dello spazio campionario.
    • Se tra i 15 studenti osservati, 4 hanno punteggi superiori a 25, qual è la proporzione sperimentale per l’evento A?

  3. Eventi Complementari
    Definiamo l’evento B: “Uno studente ha un punteggio SWLS inferiore o uguale a 25”.

    • Scrivi l’evento B in relazione all’evento A.
    • Qual è la probabilità empirica di B, sapendo che 4 studenti hanno punteggi superiori a 25?

Esercizi sulle Operazioni tra Eventi

  1. Unione di Eventi
    Definiamo due eventi:

    • A: “Il punteggio SWLS è superiore a 25”.
    • C: “Il punteggio SWLS è inferiore a 15”.
    • Scrivi l’evento A ∪ C (“Lo studente ha un punteggio maggiore di 25 o minore di 15”).
    • Se nel campione di 15 studenti, 4 studenti hanno punteggi superiori a 25 e 3 hanno punteggi inferiori a 15, qual è la proporzione empirica di A ∪ C?

  2. Intersezione di Eventi e Eventi Disgiunti
    Supponiamo che l’evento D sia: “Uno studente ha un punteggio pari a 20”.

    • L’evento D e l’evento A sono disgiunti?
    • Se nessuno degli studenti ha ottenuto esattamente 20, qual è la probabilità empirica di A ∩ D?

Esercizi sulle Regole della Probabilità 6. Probabilità dell’Unione di Eventi
Supponiamo di avere:

  • P(A) = 0.3 (probabilità che un punteggio sia superiore a 25).
  • P(C) = 0.2 (probabilità che un punteggio sia inferiore a 15).
  • P(A ∩ C) = 0 (perché un punteggio non può essere contemporaneamente superiore a 25 e inferiore a 15).
  • Usa la regola dell’unione per calcolare P(A ∪ C).

  1. Probabilità Condizionata
    Consideriamo:

    • P(A) = 0.3 (probabilità che un punteggio sia superiore a 25).
    • P(E) = 0.5 (probabilità che uno studente abbia più di 20 anni).
    • P(A | E) = 0.4 (probabilità che un soggetto con più di 20 anni abbia un punteggio superiore a 25).
    • Usa la formula della probabilità condizionata per calcolare P(A ∩ E).

Esercizi su Permutazioni e Combinazioni

  1. Selezione Casuale di Studenti
    Dal campione di 15 studenti, supponiamo di voler selezionare casualmente 3 studenti per partecipare a un’intervista sulla loro soddisfazione di vita.

    • Quanti modi ci sono per selezionare 3 studenti su 15?

  2. Ordinare gli Studenti per Discussione
    Supponiamo di voler formare un piccolo gruppo di discussione con 3 studenti, scegliendoli in ordine di intervento.

    • Quante diverse sequenze di 3 studenti possiamo ottenere?

  3. Formare Coppie di Studenti
    Se vogliamo formare coppie di studenti per un esercizio collaborativo, senza considerare l’ordine, quanti modi ci sono per farlo?

1. Definizione dello Spazio Campionario

  • Lo spazio campionario \(\Omega\) per questo esperimento è l’insieme di tutti i possibili punteggi della Satisfaction with Life Scale (SWLS), quindi:

    \[ \Omega = \{5, 6, 7, ..., 35\} \]

  • Se abbiamo raccolto i dati di 15 studenti con punteggi osservati \(\{27, 21, 15, 30, 18, 23, 26, 35, 20, 22, 19, 25, 32, 29, 28\}\), possiamo considerare \(\Omega\) come questo insieme specifico.

2. Definizione di un Evento

  • L’evento \(A\) “Uno studente ha un punteggio SWLS superiore a 25” è il sottoinsieme:

    \[ A = \{27, 30, 26, 35, 32, 29, 28\}\]

  • Se 7 studenti su 15 hanno punteggi superiori a 25, la probabilità empirica è:

    \[ P(A) = \frac{7}{15} = 0.467 \]

3. Eventi Complementari

  • L’evento complementare \(B\) “Uno studente ha un punteggio SWLS inferiore o uguale a 25” è:

    \[ B = \{21, 15, 18, 23, 20, 22, 19, 25\}\]

  • Se 8 studenti su 15 rientrano in \(B\), la probabilità empirica è:

    \[ P(B) = 1 - P(A) = \frac{8}{15} = 0.533 \]

Soluzioni agli Esercizi sulle Operazioni tra Eventi

4. Unione di Eventi

  • L’evento \(A \cup C\) (“Lo studente ha un punteggio maggiore di 25 o minore di 15”) è:

    \[ A \cup C = \{27, 30, 26, 35, 32, 29, 28, 15\}\]

  • Se 8 studenti su 15 appartengono a \(A \cup C\), la probabilità empirica è:

    \[ P(A \cup C) = \frac{8}{15} = 0.533 \]

5. Intersezione di Eventi e Eventi Disgiunti

  • L’evento \(D\) “Uno studente ha un punteggio pari a 20” è \(D = \{20\}\).

  • L’evento \(A \cap D\) è l’insieme degli elementi comuni a \(A\) e \(D\), ma \(D\) non ha elementi in \(A\), quindi:

    \[ A \cap D = \emptyset \]

  • Essendo \(A \cap D = \emptyset\), gli eventi sono disgiunti e \(P(A \cap D) = 0\).

Soluzioni agli Esercizi sulle Regole della Probabilità

6. Probabilità dell’Unione di Eventi

Usiamo la formula:

\[ P(A \cup C) = P(A) + P(C) - P(A \cap C) \]

Dato che \(P(A \cap C) = 0\), abbiamo:

\[ P(A \cup C) = 0.3 + 0.2 - 0 = 0.5 \]

7. Probabilità Condizionata

La probabilità congiunta \(P(A \cap E)\) si calcola con:

\[ P(A \cap E) = P(A | E) \cdot P(E) \]

Sostituendo i valori:

\[ P(A \cap E) = 0.4 \times 0.5 = 0.2 \]

Soluzioni agli Esercizi su Permutazioni e Combinazioni

8. Selezione Casuale di Studenti

Il numero di modi per scegliere 3 studenti su 15 (combinazioni) è:

\[ C_{15,3} = \frac{15!}{3!(15-3)!} = \frac{15!}{3!12!} = \frac{15 \times 14 \times 13}{3 \times 2 \times 1} = 455 \]

9. Ordinare gli Studenti per Discussione

Il numero di modi per scegliere e ordinare 3 studenti su 15 (disposizioni) è:

\[ D_{15,3} = \frac{15!}{(15-3)!} = \frac{15!}{12!} = 15 \times 14 \times 13 = 2730 \]

10. Formare Coppie di Studenti

Il numero di modi per formare coppie (combinazioni di 2 studenti su 15) è:

\[ C_{15,2} = \frac{15!}{2!(15-2)!} = \frac{15 \times 14}{2 \times 1} = 105 \]

Bibliografia

Chan, J. C. C., & Kroese, D. P. (2025). Statistical Modeling and Computation (2ª ed.). Springer.

  1. In termini semplici, una \(\sigma\)-algebra è l’insieme di tutti gli eventi che possiamo definire a partire dallo spazio campionario \(\Omega\), costruito in modo tale che le usuali operazioni insiemistiche (complemento, unione, intersezione, ecc.) possano sempre essere applicate senza creare contraddizioni logiche.↩︎