42. Introduzione#
In psicologia, i ricercatori vogliono trovare connessioni tra variabili e confrontare le condizioni sperimentali. La correlazione di Pearson aiuta a descrivere le relazioni tra variabili, ma non è sufficiente perché il ricercatore vuole descrivere la relazione tra le variabili nella popolazione e non solo nel campione. Il modello di regressione lineare viene utilizzato per questo scopo e utilizza la funzione matematica più semplice, la funzione lineare, per descrivere la relazione tra le variabili. Il modello di regressione lineare permette al ricercatore di fare inferenze sulla relazione tra le variabili e di comprendere le proprietà geometriche della funzione lineare. In questo e nei successivi capitoli vedremo come costruire un modello statistico basato sull’approccio bayesiano utilizzando il modello di regressione lineare.
42.1. La funzione lineare#
Iniziamo ripassando la funzione lineare. La funzione lineare è definita come:
dove \(a\) e \(b\) sono costanti. Il grafico di questa funzione è una retta, dove il parametro \(b\) rappresenta il coefficiente angolare e il parametro \(a\) rappresenta l’intercetta con l’asse delle \(y\). In altre parole, la retta interseca l’asse \(y\) nel punto \((0,a)\) se \(b \neq 0\).
Possiamo dare un’interpretazione geometrica alle costanti \(a\) e \(b\) considerando la funzione:
Questa funzione rappresenta un caso speciale, la proporzionalità diretta tra \(x\) e \(y\). Nel caso generale della funzione lineare:
aggiungiamo una costante \(a\) a ciascun valore \(y = b x\). Nella funzione lineare, se il coefficiente \(b\) è positivo, il valore di \(y\) aumenta al crescere di \(x\); se \(b\) è negativo, il valore di \(y\) diminuisce al crescere di \(x\); se \(b=0\), la retta è orizzontale e il valore di \(y\) non varia al variare di \(x\).
Consideriamo ora il coefficiente \(b\) in modo più dettagliato. Prendiamo un punto \(x_0\) e un incremento arbitrario \(\varepsilon\), come mostrato nella figura. Le differenze \(\Delta x = (x_0 + \varepsilon) - x_0\) e \(\Delta y = f(x_0 + \varepsilon) - f(x_0)\) sono chiamate “incrementi” di \(x\) e \(y\). Il coefficiente angolare \(b\) è definito come il rapporto
indipendentemente dalla grandezza degli incrementi \(\Delta x\) e \(\Delta y\). Per dare un’interpretazione geometrica al coefficiente angolare (o pendenza) della retta, possiamo semplificare assumendo \(\Delta x = 1\). In questo caso, \(b\) è uguale a \(\Delta y\).
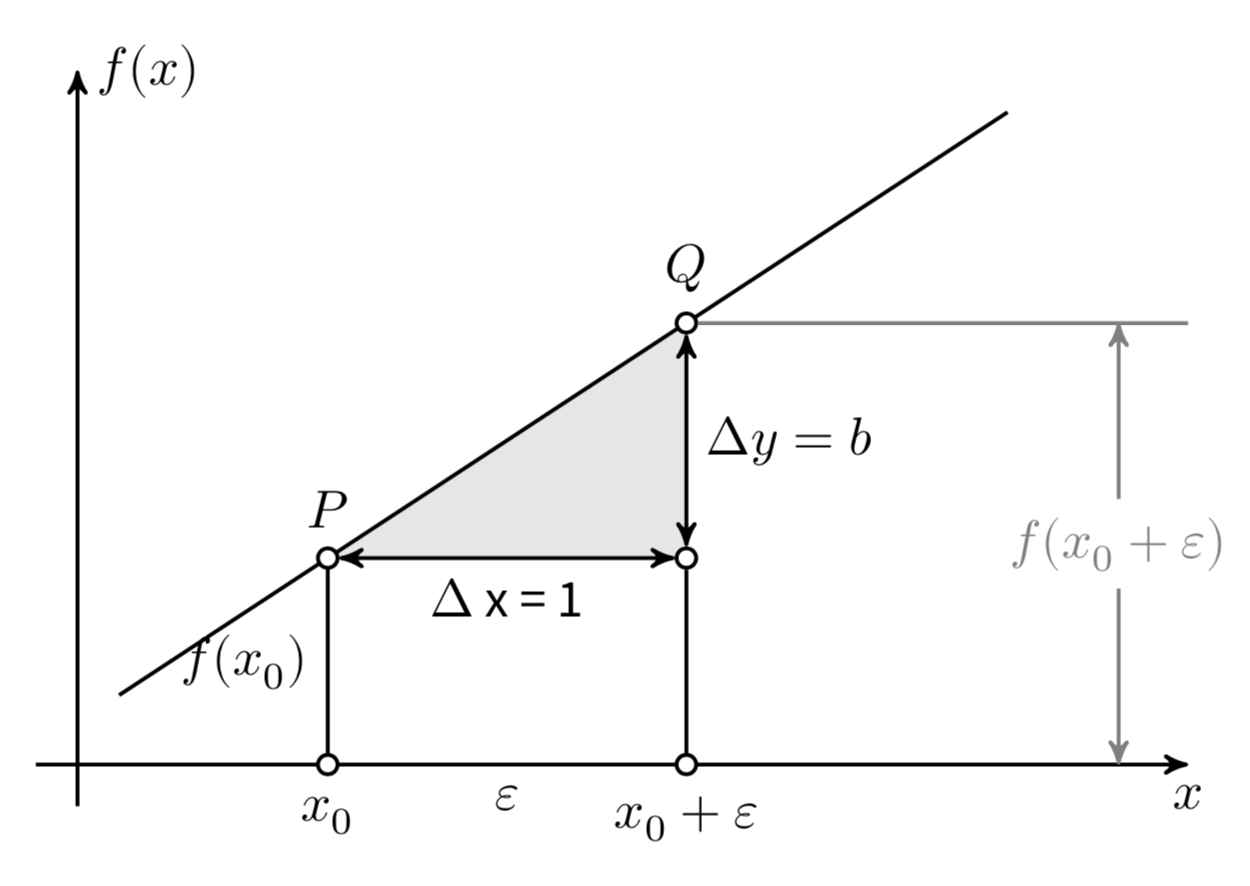
Fig. 42.1 La funzione lineare \(y = a + bx\).#
Possiamo dunque dire che la pendenza \(b\) di un retta è uguale all’incremento \(\Delta y\) associato ad un incremento unitario nella \(x\).
42.2. Una media per ciascuna osservazione#
In precedenza abbiamo visto come stimare i parametri di un modello bayesiano nel quale le osservazioni sono indipendenti e identicamente distribuite secondo una densità gaussiana,
Il modello dell’eq. (42.1) assume che ogni \(Y_i\) sia la realizzazione di una v.c. distribuita come \(\mathcal{N}(\mu, \sigma^2)\). Da un punto di vista bayesiano, questo modello può essere implementato imponendo delle distribuzioni a priori ai parametri \(\mu\) e \(\sigma\) e generando la verosimiglianza in base ai dati osservati. Per esempio, possiamo usare le seguenti distribuzioni a priori.
Con queste informazioni, possono poi essere trovate le distribuzioni a posteriori dei parametri [GHV20]. Esploreremo ora un’estensione del modello bayesiano che ci consentirà di descrivere la relazione lineare tra due variabili.
42.3. Relazione lineare tra la media \(y \mid x\) e il predittore#
Il ricercatore spesso si trova ad osservare altre variabili che sono associate ad ogni risposta \(y_i\). Una di queste variabili è chiamata \(x\) e, nel contesto del modello di regressione, viene definita come predittore o variabile indipendente. L’obiettivo del ricercatore è quello di predire il valore di una variabile \(y_i\) basandosi sul valore di \(x_i\). Ora, come possiamo estendere il modello dell’equazione (42.1) per studiare la relazione tra \(y_i\) e \(x_i\)?
Nella sua forma più basilare, un modello lineare può essere scritto come segue.
L’equazione (42.1) rappresenta un modello statistico che assume che tutte le osservazioni \(Y_i\) abbiano una media comune \(\mu\). Tuttavia, se vogliamo considerare anche una nuova variabile \(x_i\) che assume valori diversi per ogni \(Y_i\), dobbiamo modificare quel modello. In particolare, invece della media comune \(\mu\), introduciamo una media \(\mu_i\) specifica per ciascuna osservazione \(Y_i\). Questa nuova equazione, chiamata modello di regressione lineare, ci permette di studiare la relazione tra \(Y_i\) e \(x_i\) considerando \(\mu_i\) come una funzione lineare di \(x_i\).
L’eq. (42.2) afferma che ciascuna osservazione \(Y_i\) è estratta casualmente dalla distribuzione \(\mathcal{N}(\mu_i, \sigma)\), dove \(\mu_i\) è la media associata alla \(i\)-esima osservazione e \(\sigma\) è la deviazione standard comune a tutte le osservazioni. Per modellare la relazione tra il predittore \(x_i\) e la risposta \(Y_i\), il modello di regressione assume che la media della distribuzione da cui abbiamo estratto \(Y_i\), ovvero \(\mu_i\), sia una funzione lineare del predittore \(x_i\), ovvero
dove \(\beta_0\) e \(\beta_1\) sono i parametri incogniti rappresentanti l’intercetta e la pendenza della retta di regressione, rispettivamente. In altre parole, il modello di regressione suppone che esista una relazione lineare tra \(x_i\) e \(Y_i\) e che ogni valore di \(Y_i\) sia una realizzazione di una variabile casuale con media \(\mu_i\) e deviazione standard \(\sigma\).
Nell’eq. (42.3), \(x_i\) è considerata una costante nota e \(\beta_0\) e \(\beta_1\) sono variabili casuali, che vengono stimate tramite l’inferenza bayesiana. Questo procedimento consiste nell’assegnare una distribuzione a priori a \(\beta_0\) e a \(\beta_1\), trovare la verosimiglianza dei dati e calcolare la distribuzione a posteriori dei parametri \(\beta_0\) e \(\beta_1\).
Il modello dell’eq. (42.3) postula che il valore atteso di ciascuna osservazione \(Y_i\) sia una funzione lineare del corrispondente predittore \(x_i\). La costante \(\beta_0\) rappresenta il valore atteso di \(Y_i\) quando \(x_i=0\), mentre la costante \(\beta_1\) rappresenta l’incremento atteso di \(Y_i\) quando \(x_i\) aumenta di un’unità.
Va sottolineato che il modello fornisce una stima del valore atteso \(\mu_i\) e non del valore effettivo di ciascuna osservazione \(Y_i\). In altre parole, la relazione lineare tra \(\mu_i\) e \(x_i\) non può essere utilizzata per prevedere il valore esatto di \(Y_i\) per un dato valore di \(x_i\), ma solo per fornire una stima del valore atteso di \(Y_i\) per quel dato valore di \(x_i\).
42.4. Il modello lineare#
Sostituendo la relazione lineare dell’eq. (42.3) nell’eq. (42.2), otteniamo il modello di regressione lineare:
In questo modello, ogni osservazione \(Y_i\) è estratta a caso da una distribuzione Normale con media \(\beta_0 + \beta_1 x_i,\) dove \(\beta_0\) è l’intercetta e \(\beta_1\) è la pendenza della retta di regressione. La deviazione standard \(\sigma\) rappresenta la varianza comune a tutte le osservazioni. Questo modello è chiamato “lineare” perché la relazione tra \(\mathbb{E}(Y_i) = \mu_i\) e \(x_i\) è lineare e “bivariato” perché coinvolge solo due variabili, \(Y\) e \(x\).
42.4.1. Assunzioni#
Il modello di regressione lineare bivariato assume che la variabile \(x\) sia fissa e costante tra i diversi campioni. Per ogni valore di \(x\), il modello ipotizza che la variabile \(y\) segua una distribuzione Normale di media \(\mu_i = \alpha + \beta x_i\) e deviazione standard \(\sigma\), dove \(\alpha\) e \(\beta\) sono i parametri del modello. Questa è l’assunzione di normalità e linearità del modello. Il modello assume anche che le distribuzioni condizionate \(p(y \mid x_i)\) siano omoschedastiche, cioè che abbiano la stessa deviazione standard \(\sigma\) per tutti i valori di \(x_i\). Infine, il modello assume che i dati campionati siano indipendenti e che gli errori \(\varepsilon_i\) siano distribuiti in maniera Normale con media zero e deviazione standard \(\sigma\). In altre parole, il modello ipotizza che ogni osservazione \(y_i\) sia una realizzazione della variabile casuale \(Y = y_i \mid X = x_i\).
42.5. Commenti e considerazioni finali#
Il modello di regressione lineare bivariato viene utilizzato per studiare l’associazione lineare tra due variabili \(x\) e \(Y\), e per determinare la direzione e l’entità di tale legame. Inoltre, questo modello statistico consente di fare previsioni sul valore della variabile dipendente \(Y\) sulla base del valore assunto dalla variabile indipendente \(x\).
