4. Introduzione a Numpy

Anche se la Standard Library di Python offre molte funzioni utili per l’analisi dei dati, è conveniente utilizzare varie funzioni specifiche contenute in altri moduli. I moduli più utili per l’analisi dei dati sono:

• NumPy per i calcoli numerici,

• Pandas per caricare e manipolare i dati,

• Matplotlib e Seaborn per visualizzare i dati.

In questo capitolo introdurremo NumPy. NumPy è l’abbreviazione di Numerical Python: un’estensione del linguaggio pensata per il calcolo algebrico e matriciale. Numpy consente di lavorare con vettori e matrici in maniera più efficiente e veloce di quanto non si possa fare con le liste e le liste di liste (matrici) di Python. Inoltre, Numpy aggiunge una serie di funzioni matematiche di base e la possibilità di generare numeri casuali.

4.1. Gli array nel modulo NumPy

In Python puro abbiamo a disposizione oggetti numerici (interi e a virgola mobile) e contenitori (liste, dizionari e insiemi). Numpy fornisce un nuovo tipo di dato: un array N-dimensionale (ndarray). Il costrutto ndarray è un oggetto di tipo array multidimensionale caratterizzato da alcune proprietà, come:

• dimensioni: gli ndarray possono avere da una a un numero arbitrario di dimensioni, che vengono definite come “assi”. Ad esempio, un array può essere unidimensionale (un vettore), bidimensionale (una matrice), tridimensionale (un cubo), e così via;

• tipo di dato: tutti gli elementi di un ndarray devono avere lo stesso tipo di dato, che può essere ad esempio float, int, bool o string (questo li differenzia dalle liste in puro Python, che non sono omogenee);

• forma: la forma di un ndarray indica le dimensioni dell’array, cioè il numero di elementi per ogni asse. Ad esempio, un array con forma (3, 4) ha 3 righe e 4 colonne;

• indicizzazione: gli ndarray possono essere indicizzati come gli array Python standard, ma consentono anche indicizzazioni più avanzate.

Gli ndarray offrono una vasta gamma di funzioni e metodi per manipolare e analizzare i dati in essi contenuti, tra cui operazioni matematiche, statistiche, trasformazioni e manipolazioni di dati.

Terminologia

• Con size di un array intendiamo il numero di elementi presenti in un array;

• Con rank di un array si intende il numero di assi/dimensioni di un array;

• Con shape di un array intendiamo le dimensioni dell’array, cioè una tupla di interi contenente il numero di elementi per ogni dimensione.

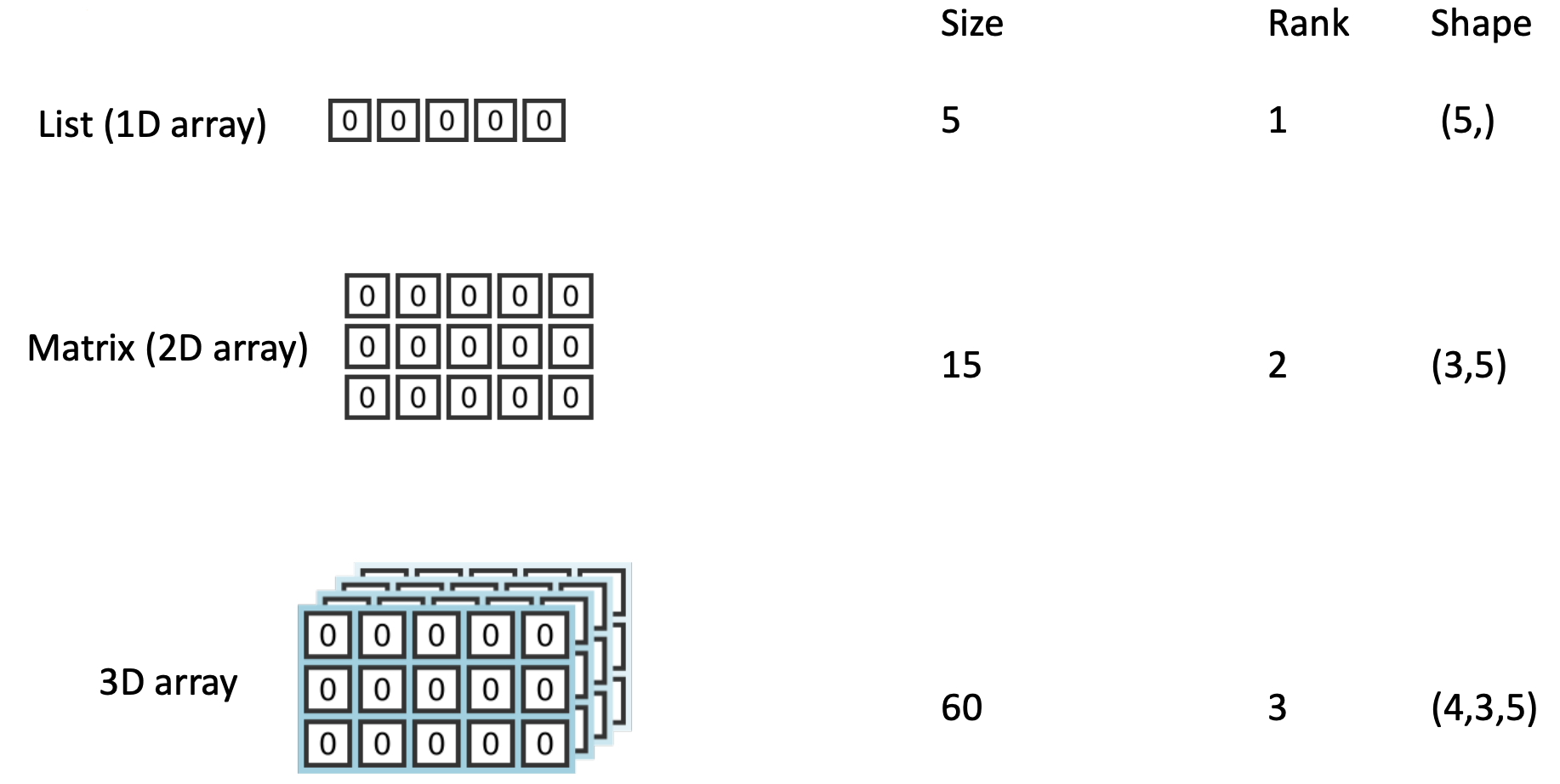
Creare ndarray

Il modo più semplice per creare un ndarray è quello di convertire una lista Python. Per esempio, possiamo creare un array 1-D nel modo seguente:

import numpy as np

a = np.array([1, 2, 3, 4, 5, 6])

L’istruzione precedente ha creato un vettore, chiamato a, con 6 elementi che sono i numeri interi indicati in parentesi quadra:

a

array([1, 2, 3, 4, 5, 6])

Indicizzazione

Se voglio estrarre un singolo elemento del vettore lo indicizzo con la sua posizione (si ricordi che l’indice inizia da 0):

a[0]

1

a[2]

3

Un array 2-D si crea nel modo seguente:

a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
a

array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

Estraggo un singolo elemento dall’array:

print(a[0, 2]) 

3

Estraggo una riga dall’array:

print(a[1]) 

[5 6 7 8]

Estraggo una colonna dall’array:

print(a[:, 1]) 

[ 2  6 10]

Estraggo una sotto-matrice dall’array:

print(a[:2, 1:3]) 

[[2 3]
 [6 7]]

4.1.1. Funzioni per ndarray

Numpy offre varie funzioni per creare ndarray. Per esempio, è possibile creare un array 1-D con la funzione .arange(start, stop, incr, dtype=..) che fornisce l’intervallo di numeri compreso fra start, stop, al passo incr:

b = np.arange(2, 9, 2)
b

array([2, 4, 6, 8])

Si usa spesso .arange per creare sequenze a incrementi unitari:

x = np.arange(11)
x

array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10])

Un’altra funzione molto utile è .linspace:

x = np.linspace(0, 10, num=20)
x

array([ 0.        ,  0.52631579,  1.05263158,  1.57894737,  2.10526316,
        2.63157895,  3.15789474,  3.68421053,  4.21052632,  4.73684211,
        5.26315789,  5.78947368,  6.31578947,  6.84210526,  7.36842105,
        7.89473684,  8.42105263,  8.94736842,  9.47368421, 10.        ])

Fissati gli estremi (qui 0, 10) e il numero di elementi desiderati, .linspace determina in maniera automatica l’incremento.

Una proprietà molto utile dei ndarray è la possibilità di filtrare gli elementi di un array che rispondono come True ad un criterio. Per esempio:

x[x > 7]

array([ 7.36842105,  7.89473684,  8.42105263,  8.94736842,  9.47368421,
       10.        ])

perché solo gli ultimi sei elementi di x rispondono True al criterio \(x > 7\).

Le dimensioni (“assi”) di un ndarray vengono ritornate dal metodo .dim. Per esempio:

a

array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

a.ndim

2

Il numero di elementi per ciascun asse viene ritornato dal metodo .shape:

a.shape

(3, 4)

4.2. Operazioni sugli array

Numpy è uno strumento molto utile per eseguire operazioni algebriche sugli elementi degli array. Spesso, ci limiteremo ad utilizzare array che rappresentano vettori (ovvero array di rank 1), in cui gli elementi del vettore possono rappresentare, ad esempio, le misure ottenute su una qualche variabile. Utilizzando Numpy, siamo in grado di automatizzare le comuni operazioni aritmetiche che normalmente svolgiamo su coppie di numeri, ma applicandole a tutti gli elementi dell’array. Questo permette di lavorare in modo molto efficiente con grandi quantità di dati e di effettuare analisi su di essi con facilità.

Supponiamo, ad esempio, di volere calcolare l’indice BMI:

\[ BMI = \frac{kg}{m^2}. \]

Supponiamo inoltre di avere raccolto i dati di 4 individui:

m = np.array([1.62, 1.75, 1.55, 1.74])
kg = np.array([55.4, 73.6, 57.1, 59.5])
m, kg

(array([1.62, 1.75, 1.55, 1.74]), array([55.4, 73.6, 57.1, 59.5]))

dove m è l’array che contiene i dati relativi all’altezza in metri dei quattro individui e kg è l’array che contiene i dati relativi al peso in kg. I dati sono organizzati in modo tale che il primo elemento di entrambi i vettori si riferisce alle misure del primo individuo, il secondo elemento dei due vettori si riferisce alle misure del secondo individuo, ecc. Per il primo individuo del campione, l’indice di massa corporea è

55.4 / 1.62**2

21.109586953208346

Si noti che non abbiamo bisogno di scrivere 55.4 / (1.62**2) in quanto, in Python, l’elevazione a potenza viene eseguita prima della somma e della divisione (come in tutti i linguaggi). Usando i dati immagazzinati nei due vettori, lo stesso risultato si ottiene nel modo seguente:

kg[0] / m[0]**2

21.109586953208346

Se ora non specifichiamo l’indice (per esempio, [0]), le operazioni aritmetiche indicate verranno eseguite per ciascuna coppia di elementi corrispondenti nei due vettori:

bmi = kg / m**2

Otteniamo così, con una sola istruzione, l’indice BMI dei quattro individui:

bmi.round(1)

array([21.1, 24. , 23.8, 19.7])

Questo esempio mostra come le normali operazioni aritmetiche vengano applicate sugli array elemento per elemento.

4.3. Broadcasting

Il broadcasting è un meccanismo che consente a Numpy di eseguire operazioni tra array di diverse dimensioni o tra un array e uno scalare, anche quando le dimensioni non sono compatibili tra loro. In questo modo, Numpy può estendere automaticamente la dimensione di uno degli operandi in modo da rendere possibile l’operazione.

Ad esempio, è possibile effettuare un’operazione tra un array e un singolo numero (operazione tra un vettore e uno scalare), oppure tra array di due dimensioni diverse, senza dover esplicitamente allineare le dimensioni degli array. In questi casi, Numpy utilizza il broadcasting per allineare le dimensioni degli array in modo da eseguire l’operazione richiesta. Questo rende il codice più compatto e leggibile, e consente di evitare il lavoro manuale di espansione degli array.

In sintesi, il broadcasting è un meccanismo molto utile in Numpy che consente di eseguire operazioni tra array di diverse dimensioni o tra un array e uno scalare in modo automatico, senza dover esplicitamente allineare le dimensioni degli array.

Ad esempio

a

array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

a * 2

array([[ 2,  4,  6,  8],
       [10, 12, 14, 16],
       [18, 20, 22, 24]])

4.4. Altre operazioni sugli array

C’è un numero enorme di funzioni predefinite in NumPy che calcolano automaticamente diverse quantità sui ndarray. Ad esempio:

• mean(): calcola la media di un vettore o matrice;

• sum(): calcola la somma di un vettore o matrice;

• std(): calcola la deviazione standard;

• min(): trova il minimo nel vettore o matrice;

• max(): trova il massimo;

• ndim: dimensione del vettore o matrice;

• shape: restituisce una tupla con la “forma” del vettore o matrice;

• size: restituisce la dimensione totale del vettore (=ndim) o della matrice;

• dtype: scrive il tipo numpy del dato;

• zeros(num): scrive un vettore di num elementi inizializzati a zero;

• arange(start,stop,step): genera un intervallo di valori (interi o reali, a seconda dei valori di start, ecc.) intervallati di step. Nota che i dati vengono generati nell’intervallo aperto [start,stop)!

• linstep(start,stop,num): genera un intervallo di num valori interi o reali a partire da start fino a stop (incluso!);

• astype(tipo): converte l’ndarray nel tipo specificato

Per esempio:

x = np.array([1, 2, 3])
x

array([1, 2, 3])

[x.min(), x.max(), x.sum(), x.mean(), x.std()]

[1, 3, 6, 2.0, 0.816496580927726]

4.5. Lavorare con formule matematiche

L’implementazione delle formule matematiche sugli array è un processo molto semplice con Numpy. Possiamo prendere ad esempio la formula della deviazione standard che discuteremo nel capitolo Indici di posizione e di scala:

\[ s = \sqrt{\sum_{i=1}^n\frac{(x_i - \bar{x})^2}{n}} \]

L’implementazione su un array NumPy è la seguente:

np.sqrt(np.sum((x - np.mean(x)) ** 2) / np.size(x))

0.816496580927726

Questa implementazione funziona nello stesso modo sia che x contenga 3 elementi (come nel caso presente) sia che x contenga migliaia di elementi. È importante notare l’utilizzo delle parentesi tonde per specificare l’ordine di esecuzione delle operazioni. In particolare, nel codice fornito, si inizia calcolando la media degli elementi del vettore x per mezzo della funzione np.mean(x). Questa operazione produce uno scalare, ovvero un singolo valore numerico che rappresenta la media degli elementi del vettore. L’utilizzo delle parentesi tonde è fondamentale per garantire l’ordine corretto delle operazioni. In questo caso, la funzione np.mean() viene applicata al vettore x prima di qualsiasi altra operazione matematica. Senza le parentesi tonde, le operazioni verrebbero eseguite in un ordine diverso e il risultato potrebbe essere errato.

np.mean(x)

2.0

Successivamente, eseguiamo la sottrazione dei singoli elementi del vettore x per la media del vettore stesso, ovvero \(x_i - \bar{x}\), utilizzando il meccanismo del broadcasting.

x - np.mean(x)

array([-1.,  0.,  1.])

Eleviamo poi al quadrato gli elementi del vettore che abbiamo ottenuto:

(x - np.mean(x)) ** 2

array([1., 0., 1.])

Sommiamo gli elementi del vettore:

np.sum((x - np.mean(x)) ** 2)

2.0

Dividiamo il numero ottenuto per \(n\). Questa è la varianza di \(x\):

res = np.sum((x - np.mean(x)) ** 2) / np.size(x)
res

0.6666666666666666

Infine, per ottenere la deviazione standard, prendiamo la radice quadrata:

np.sqrt(res)

0.816496580927726

Il risultato ottenuto coincide con quello che si trova applicando la funzione np.std():

np.std(x)

0.816496580927726

4.6. Slicing

Per concludere, spendiamo ancora alcune parole sull’indicizzazione degli ndarray.

Slicing in Numpy è un meccanismo che consente di selezionare una porzione di un array multidimensionale, ovvero una sotto-matrice o un sotto-vettore. Per selezionare una porzione di un array, si utilizza la sintassi [start:stop:step], dove start indica l’indice di partenza della porzione, stop indica l’indice di fine e step indica il passo da utilizzare per la selezione. Se uno o più di questi valori vengono omessi, vengono utilizzati dei valori di default.

Ad esempio, se abbiamo un array arr di dimensione (3, 4) e vogliamo selezionare la seconda colonna, possiamo usare la sintassi arr[:, 1]. In questo caso, il simbolo : indica che vogliamo selezionare tutte le righe, mentre il numero 1 indica che vogliamo selezionare la seconda colonna.

Inoltre, possiamo utilizzare il meccanismo di slicing anche per selezionare porzioni di array multidimensionali. Ad esempio, se abbiamo un array arr di dimensione (3, 4, 5) e vogliamo selezionare la prima riga di ciascuna matrice 4x5, possiamo usare la sintassi arr[:, 0, :].

Per esempio, creiamo l’array a di rank 2 con shape (3, 4):

a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
a

array([[ 1,  2,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

Utilizziamo il meccanismo di slicing per estrarre la sottomatrice composta dalle prime 2 righe e dalle colonne 1 e 2. b è l’array risultante di dimensione (2, 2):

b = a[:2, 1:3]
b

array([[2, 3],
       [6, 7]])

È importante sapere che uno slice di un array in Numpy è una vista degli stessi dati, il che significa che modificarlo implica la modifica dell’array originale. In pratica, quando si modifica uno slice di un array, si sta modificando direttamente l’array originale e tutte le altre visualizzazioni dell’array vedranno la stessa modifica. Questo avviene perché Numpy è progettato per gestire enormi quantità di dati, pertanto cerca di evitare il più possibile di effettuare copie dei dati.

Questo comportamento deve essere preso in considerazione durante la modifica degli array in Numpy, al fine di evitare modifiche accidentali o indesiderate. In alcuni casi, è possibile utilizzare il metodo copy() per creare una copia indipendente di un array e lavorare sulla copia senza modificare l’originale. Vediamo un esempio.

print(a[0, 1])   

2

b[0, 0] = 77     

print(a)

[[ 1 77  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]

c = a.copy()
c

array([[ 1, 77,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

c[0, 1] = 33
c 

array([[ 1, 33,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

a

array([[ 1, 77,  3,  4],
       [ 5,  6,  7,  8],
       [ 9, 10, 11, 12]])

4.7. Alcuni esercizi

Esercizio 1. Creare un vettore nullo di dimensione 10 ma con il quinto valore che è 1.

Z = np.zeros(10)
Z[4] = 1
print(Z)

[0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]

Esercizio 2. Creare un vettore con valori compresi tra 10 e 49.

Z = np.arange(10,50)
print(Z)

[10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33
 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49]

Esercizio 3. Invertire un vettore (il primo elemento diventa l’ultimo).

Z = np.arange(50)
Z = Z[::-1]
print(Z)

[49 48 47 46 45 44 43 42 41 40 39 38 37 36 35 34 33 32 31 30 29 28 27 26
 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10  9  8  7  6  5  4  3  2
  1  0]

Esercizio 4. Trovare gli indici degli elementi non zero di [1, 2, 0, 0, 4, s0].

nz = np.nonzero([1, 2, 0, 0, 4, 0])
print(nz)

(array([0, 1, 4]),)

Esercizio 5. Crearere un array 10x10 con valori casuali e trovare i valori minimo e massimo.

Z = np.random.random((10,10))
Z

array([[0.29566218, 0.07209904, 0.35332919, 0.17613161, 0.13391945,
        0.57731849, 0.41298507, 0.4809542 , 0.57433838, 0.72957868],
       [0.18640182, 0.66723416, 0.0407446 , 0.26738269, 0.24718803,
        0.47680873, 0.47072577, 0.63904453, 0.04946509, 0.33676786],
       [0.15125694, 0.8035235 , 0.72766822, 0.03438623, 0.56261862,
        0.03090156, 0.209693  , 0.12027029, 0.86728407, 0.51087234],
       [0.94761609, 0.18013895, 0.1680644 , 0.59995202, 0.09717564,
        0.91963116, 0.17587328, 0.64455788, 0.30834252, 0.82574848],
       [0.6899722 , 0.69509972, 0.10051478, 0.07622821, 0.29633028,
        0.67208699, 0.13937026, 0.83126654, 0.3104716 , 0.76731281],
       [0.64812954, 0.04440751, 0.47189853, 0.55179952, 0.66835545,
        0.63658262, 0.57851444, 0.65999838, 0.70994299, 0.98499404],
       [0.12079029, 0.09187898, 0.11098002, 0.75410306, 0.69841245,
        0.83393347, 0.2519411 , 0.79543767, 0.18990006, 0.22595004],
       [0.2890142 , 0.48426716, 0.45908661, 0.05280785, 0.81542816,
        0.97108334, 0.83090115, 0.73187488, 0.83690497, 0.10128815],
       [0.51259079, 0.47047472, 0.93100573, 0.07936726, 0.83751339,
        0.82553189, 0.41575224, 0.93089083, 0.96169131, 0.27786872],
       [0.15652985, 0.06837039, 0.36166762, 0.89879225, 0.83833477,
        0.05479137, 0.66072095, 0.64738471, 0.2158381 , 0.81295894]])

Zmin, Zmax = Z.min(), Z.max()
print(Zmin, Zmax)

0.03090156322332782 0.9849940363190897

Esercizio 6. Creare un vettore casuale di dimensione 30 e trovare il valore medio.

Z = np.random.random(30)
Z

array([0.15123162, 0.2472526 , 0.11559576, 0.84466421, 0.17906644,
       0.0357539 , 0.28023086, 0.25575024, 0.53928608, 0.30876137,
       0.34168444, 0.0858696 , 0.53987245, 0.74778262, 0.75887193,
       0.53039622, 0.01393338, 0.19079128, 0.20914176, 0.74098076,
       0.47250913, 0.26713233, 0.36957794, 0.05939173, 0.94049557,
       0.05371031, 0.0333191 , 0.33840475, 0.2016945 , 0.29382054])

m = Z.mean()
print(m)

0.3382324482187053

Esercizio 7. Dato un array 1D, negare tutti gli elementi compresi tra 3 e 8, inplace.

Z = np.arange(11)
Z[(3 < Z) & (Z < 8)] *= -1
print(Z)

[ 0  1  2  3 -4 -5 -6 -7  8  9 10]

Qual è l’output di print(sum(range(5),-1))?

print(sum(range(5),-1))

9

Esercizio 8. Creare un vettore casuale di dimensione 10 e sostituire il valore massimo con 0.

Z = np.random.random(10)
Z[Z.argmax()] = 0
print(Z)

[0.         0.02184702 0.69490615 0.77493786 0.18293928 0.57745408
 0.38753123 0.64654879 0.4242353  0.55342575]

Esercizio 9. Trovare il valore più vicino (a uno scalare dato) in un vettore.

Z = np.arange(100)
Z

array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15, 16,
       17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33,
       34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50,
       51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67,
       68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84,
       85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99])

v = np.random.uniform(0, 100)
v

18.959027637392566

index = (np.abs(Z - v)).argmin()
print(Z[index])

19

Esercizio 10. Convertire tutti gli elementi di un array numpy da float a integer.

a = np.array([[2.5, 3.8, 1.5], [4.7, 2.9, 1.56]])

o = a.astype("int")

print(o)

[[2 3 1]
 [4 2 1]]

Esercizio 11. Convertire un array numpy binario (contenente solo 0 e 1) in un array numpy booleano.

a = np.array([[1, 0, 0], [1, 1, 1], [0, 0, 0]])

o = a.astype("bool")

print(o)

[[ True False False]
 [ True  True  True]
 [False False False]]

Esercizio 12. Unire orizzontalmente due array numpy aventi la stessa prima dimensione (cioè lo stesso numero di righe negli array 2D).

a1 = np.array([[1, 2, 3], [4, 5, 6]])

a2 = np.array([[7, 8, 9], [10, 11, 12]])

o = np.hstack((a1, a2))

print(o)

[[ 1  2  3  7  8  9]
 [ 4  5  6 10 11 12]]

Esercizio 13. Dati due array numpy, estrarre gli indici in cui gli elementi nei due array corrispondono.

a = np.array([1, 2, 3, 4, 5])

b = np.array([1, 3, 2, 4, 5])

print(np.where(a == b))

(array([0, 3, 4]),)

Esercizio 14. Generare un array ripetendo un array più piccolo di 2 dimensioni 10 volte.

a = np.array([[1, 2, 3], [4, 5, 6]])

o = np.tile(a, 10)

print(o)

[[1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3]
 [4 5 6 4 5 6 4 5 6 4 5 6 4 5 6 4 5 6 4 5 6 4 5 6 4 5 6 4 5 6]]

Esercizio 15. Generare un array 5x5 di interi casuali compresi tra 0 (incluso) e 10 (escluso).

np.random.seed(123)  # setting the seed

o = np.random.randint(0, 10, size=(5, 5))

print(o)

[[2 2 6 1 3]
 [9 6 1 0 1]
 [9 0 0 9 3]
 [4 0 0 4 1]
 [7 3 2 4 7]]

Esercizio 16. Verificare se uno qualsiasi degli elementi di un array dato è diverso da zero.

x = np.array([1, 0, 0, 0])
print(np.any(x))
x = np.array([0, 0, 0, 0])
print(np.any(x))

True
False

Esercizio 17. Creare un confronto elemento per elemento (uguale, uguale entro una tolleranza) di due array dati.

x = np.array([72, 79, 85, 90, 150, -135, 120, -10, 60, 100])
y = np.array([72, 79, 85, 90, 150, -135, 120, -10, 60, 100.000001])
print(np.equal(x, y))
print(np.allclose(x, y))

[ True  True  True  True  True  True  True  True  True False]
True

Esercizio 18. Trovare i dati mancanti in un array dato.

nums = np.array([[3, 2, np.nan, 1], [10, 12, 10, 9], [5, np.nan, 1, np.nan]])
nums

array([[ 3.,  2., nan,  1.],
       [10., 12., 10.,  9.],
       [ 5., nan,  1., nan]])

print(np.isnan(nums))

[[False False  True False]
 [False False False False]
 [False  True False  True]]

Esercizio 19. Scrivi un programma NumPy per estrarre tutti i numeri da un array dato che sono inferiori e superiori ad un numero specificato.

nums = np.array([[5.54, 3.38, 7.99], [3.54, 4.38, 6.99], [1.54, 2.39, 9.29]])
n = 6
print(nums[nums < n])

[5.54 3.38 3.54 4.38 1.54 2.39]

Esercizio 20. Sostituire tutti i numeri in un array dato che sono uguali, minori e maggiori di un dato numero.

nums = np.array([[5.54, 3.38, 7.99], [3.54, 8.32, 6.99], [1.54, 2.39, 9.29]])
n = 8.32
r = 18.32
print(np.where(nums == n, r, nums))

[[ 5.54  3.38  7.99]
 [ 3.54 18.32  6.99]
 [ 1.54  2.39  9.29]]

print("\nReplace elements with of the said array which are less than", n, "with", r)
print(np.where(nums < n, r, nums))

Replace elements with of the said array which are less than 8.32 with 18.32
[[18.32 18.32 18.32]
 [18.32  8.32 18.32]
 [18.32 18.32  9.29]]

print("\nReplace elements with of the said array which are greater than", n, "with", r)
print(np.where(nums > n, r, nums))

Replace elements with of the said array which are greater than 8.32 with 18.32
[[ 5.54  3.38  7.99]
 [ 3.54  8.32  6.99]
 [ 1.54  2.39 18.32]]

Esercizio 21. Moltiplicare due array dati della stessa dimensione elemento per elemento.

nums1 = np.array([[2, 5, 2], [1, 5, 5]])
nums2 = np.array([[5, 3, 4], [3, 2, 5]])

print(nums1)

[[2 5 2]
 [1 5 5]]

print(nums2)

[[5 3 4]
 [3 2 5]]

print(np.multiply(nums1, nums2))

[[10 15  8]
 [ 3 10 25]]

4.8. Watermark

%load_ext watermark
%watermark -n -u -v -iv -w -p pytensor

Last updated: Sat Jun 17 2023

Python implementation: CPython
Python version       : 3.11.3
IPython version      : 8.12.0

pytensor: 2.12.2

numpy: 1.24.3

Watermark: 2.3.1