32. Approssimazione della distribuzione a posteriori

In sintesi, il problema bayesiano consiste nel determinare la distribuzione a posteriori di un parametro \(\theta\), data una densità di dati osservati \(y\) e una densità a priori \(p(\theta)\). Questa distribuzione può essere calcolata utilizzando il teorema di Bayes

\[ p(\theta \mid y) = \frac{p(y \mid \theta) p(\theta)}{p(y)} \]

ma il calcolo dell’evidenza \(p(y)\)

\[ p(y) = \int_{\theta} p(y \mid \theta) p(\theta) \,\operatorname {d}\! \theta. \]

può essere complesso e non sempre analitico per modelli complessi.

L’utilizzo di distribuzioni a priori coniugate consente di determinare la distribuzione a posteriori in modo analitico, ma limita le scelte del ricercatore. Per modelli più complessi, i metodi di campionamento Monte Carlo basati su Catena di Markov rappresentano una potente alternativa per la costruzione della distribuzione a posteriori, poiché consentono di determinarla sulla base di considerazioni teoriche senza vincoli sulle scelte delle distribuzioni a priori o di verosimiglianza.

In generale, il calcolo della distribuzione a posteriori in un problema bayesiano richiede l’uso di metodi computazionalmente intensivi eseguibili solo attraverso l’uso di software. Tuttavia, grazie alla crescente potenza di calcolo dei computer negli ultimi anni, i metodi bayesiani di analisi dati sono diventati sempre più popolari, poiché tali calcoli sono ora accessibili a tutti.

In questo capitolo esploreremo due metodi alternativi per il calcolo della distribuzione a posteriori nei casi in cui la distribuzione a priori coniugata non è applicabile.

• Il primo metodo, noto come metodo basato su griglia, implica la costruzione di una griglia di valori del parametro \(\theta\) e il calcolo della densità a posteriori in ogni punto della griglia. Anche se non è disponibile alcuna formula chiusa per la densità a posteriori, questo metodo permette di calcolare con precisione arbitraria le proprietà della distribuzione a posteriori.

• Il secondo metodo, noto come metodo Monte Carlo, utilizza funzioni di numeri casuali appropriate per generare un ampio campione di osservazioni della distribuzione a posteriori. Le proprietà di interesse possono poi essere stimate empiricamente sulla base del campione ottenuto. Questo metodo è particolarmente utile quando la distribuzione a posteriori è complessa o quando la griglia di valori del parametro \(\theta\) è troppo grande per essere computazionalmente gestibile.

Entrambi i metodi sono utilizzati comunemente in ambito bayesiano e offrono una soluzione alle situazioni in cui la distribuzione a priori coniugata non è applicabile.

32.1. Metodo basato su griglia

Il metodo numerico esatto basato su griglia consiste nell’approssimare la distribuzione a posteriori utilizzando una griglia di punti uniformemente spaziati quando non è possibile utilizzare una distribuzione a priori coniugata (è la procedura che abbiamo già discusso negli esempi dei capitoli precedenti; l’unica novità che introduciamo ora è la specificazione della distribuzione a priori mediante una distribuzione continua). Nonostante la maggior parte dei parametri siano continui, l’approssimazione della distribuzione a posteriori può essere ottenuta considerando solo una griglia finita di valori dei parametri. Il metodo prevede quattro fasi:

1. fissare una griglia discreta di possibili valori dei parametri;

2. valutare la distribuzione a priori e la funzione di verosimiglianza per ciascun valore della griglia;

3. calcolare la densità a posteriori approssimata, moltiplicando la distribuzione a priori per la funzione di verosimiglianza per ciascun valore della griglia e normalizzando i prodotti in modo che la loro somma sia uguale a 1;

4. selezionare \(n\) valori casuali della griglia per ottenere un campione casuale delle densità a posteriori normalizzate.

Questo metodo può essere migliorato aumentando il numero di punti della griglia, ma il limite principale è che al crescere della dimensionalità dello spazio dei parametri, i punti della griglia necessari per una buona stima aumentano esponenzialmente, rendendo il metodo impraticabile per problemi complessi.

32.1.1. Modello Beta-Binomiale

Per fare un esempio, consideriamo l’applicazione del metodo basato su griglia allo schema beta-binomiale utilizzando i dati di Zetsche et al. [ZBR19]. Supponiamo di essere interessati alla probabilità che l’aspettativa sull’umore futuro sia distorta negativamente (“successo”) – parametro \(\theta\). Vengono osservate 30 persone [gli individui clinicamente depressi di Zetsche et al. [ZBR19]]. Il modello di questo esperimento casuale è dunque Binomiale, con \(n\) = 30 e \(\theta\) incognito.

Prima di analizzare i dati, stabiliamo una distribuzione a priori per la variabile \(\theta\) utilizzando una distribuzione beta con parametri \(2\) e \(10\). Questi parametri sono stati scelti arbitrariamente e sono stati utilizzati solo come esempio. Quindi, il modello diventa:

\[\begin{split} \begin{align} Y \mid \theta & \sim Bin(n = 30, \theta), \notag\\ \theta & \sim Beta(2, 10).\notag \end{align} \end{split}\]

I dati corrispondono alle opinioni dei 30 individui clinicamente depressi del campione. In queste circostanze, l’aggiornamento bayesiano produce una distribuzione a posteriori Beta di parametri 25 (\(y + \alpha\) = 23 + 2) e 17 (\(n - y + \beta\) = 30 - 23 + 10):

\[ \theta \mid (y = 23) \sim Beta(25, 17). \]

Di seguito viene presentato un esempio di codice che implementa il metodo basato su griglia per ottenere un’approssimazione della distribuzione a posteriori per il caso dello schema beta-binomiale, dove la distribuzione a priori su \(\theta\) è impostata su \(Beta(2, 10)\):

import numpy as np
import pandas as pd
import scipy as sp
import seaborn as sns
from scipy.stats import norm
from scipy.stats import binom
from scipy.stats import beta
import scipy.stats as st
import statsmodels.api as sm
from statsmodels.graphics import tsaplots
import matplotlib.pyplot as plt
import arviz as az
import warnings

warnings.filterwarnings("ignore")
pd.options.mode.chained_assignment = None

%matplotlib inline
%config InlineBackend.figure_format = 'retina'
# Initialize random number generator
RANDOM_SEED = 8927
rng = np.random.default_rng(RANDOM_SEED)

plt.style.use("bmh")
plt.rcParams["figure.figsize"] = [10, 6]
plt.rcParams["figure.dpi"] = 100
plt.rcParams["figure.facecolor"] = "white"

sns.set_theme(palette="colorblind")

%load_ext autoreload
%autoreload 2
%config InlineBackend.figure_format = "svg"

def posterior_grid_approx(n_gridpoints, prior_params, data):
    """
    n_gridpoints: numero di punti della griglia
    prior_params: parametri della distribuzione a priori Beta (alpha, beta)
    data: dati osservati (y, n)
    """

    # Fase 1: definizione della griglia
    p_grid = np.linspace(0, 1, n_gridpoints)

    # Fase 2: valutazione della distribuzione a priori
    unstd_prior = st.beta.pdf(p_grid, prior_params[0], prior_params[1])
    prior = unstd_prior / sum(unstd_prior)

    # Fase 3: valutazione della funzione di verosimiglianza
    likelihood = st.binom.pmf(data[0], data[1], p_grid)

    # Fase 4: calcolo della densità a posteriori non normalizzata
    unstd_posterior = likelihood * prior

    # Fase 5: calcolo della densità a posteriori normalizzata
    posterior = unstd_posterior / unstd_posterior.sum()

    return p_grid, posterior

La funzione posterior_grid_approx prende in input il numero di punti della griglia grid_points, i parametri della distribuzione a priori prior_params (vettore con i valori \(\alpha\) e \(\beta\)) e i dati osservati data (vettore con i valori \(y\) e \(n\)).

• La griglia viene definita nella Fase 1 utilizzando la funzione linspace di NumPy per creare un array di punti uniformemente spaziati tra 0 e 1.

• Nella Fase 2, viene valutata la distribuzione a priori e la funzione di verosimiglianza per ogni punto della griglia. La distribuzione a priori è implementata utilizzando la funzione beta di SciPy.

• Nella Fase 3, viene valutata la funzione di verosimiglianza per ogni punto della griglia. La funzione di verosimiglianza è calcolata utilizzando la funzione binom.pmf di SciPy per la distribuzione binomiale.

• Nella Fase 4, viene calcolata la densità a posteriori non normalizzata, ovvero il prodotto della distribuzione a priori e della funzione di verosimiglianza per ogni punto della griglia.

• Nella Fase 5, viene calcolata la densità a posteriori normalizzata, ovvero il prodotto della distribuzione a priori e della funzione di verosimiglianza per ogni punto della griglia, normalizzata in modo che la somma di tutti i prodotti sia uguale a 1.

Fissiamo una griglia di \(n = 1000\) valori equispaziati. Usando la funzione precedente, creaiamo un grafico della stima della distribuzione a posteriori a cui è stata sovrapposta l’esatta distribuzione a posteriori \(Beta(25, 17)\)).

points = 1000
prior_params = np.array([2, 10])
data = np.array([23, 30])
p_grid, posterior = posterior_grid_approx(points, prior_params, data)
plt.plot(p_grid, posterior, "-", label="y = {}\nn = {}".format(data[0], data[1]))

# Parameters of the posterior distribution
alpha_prior = 2
beta_prior = 10
y = 23
n = 30
alpha_post = alpha_prior + y
beta_post = beta_prior + n - y
x = np.linspace(
    st.beta.ppf(0.01, alpha_post, beta_post),
    st.beta.ppf(0.99, alpha_post, beta_post),
    1000,
)
plt.plot(
    x,
    st.beta.pdf(x, alpha_post, beta_post) / 1000,
    "r--",
    lw=3,
    alpha=0.75,
    label="Beta(25, 17)",
)

plt.xlabel("Probabilità di un'aspettativa negativa")
plt.ylabel("Densità")
plt.title("Distribuzione a posteriori")
plt.legend(loc=0)

<matplotlib.legend.Legend at 0x105fe2e10>

In sintesi, l’approccio basato sulla griglia è intuitivo e non richiede competenze di programmazione avanzate per essere implementato. Inoltre, fornisce un risultato che può essere considerato, per tutti gli scopi pratici, come un campione casuale estratto dalla distribuzione di probabilità a posteriori condizionata ai dati. Tuttavia, questo metodo ha un uso limitato a causa della maledizione della dimensionalità1, il che significa che può essere applicato solo a modelli statistici semplici con non più di due parametri. Pertanto, in pratica, viene spesso sostituito da altre tecniche più efficienti, poiché i modelli utilizzati in psicologia spesso richiedono la stima di centinaia o addirittura migliaia di parametri.

32.2. Metodo Monte Carlo

I metodi più comuni per ottenere la distribuzione a posteriori in modelli complessi nell’analisi bayesiana sono i metodi di campionamento MCMC. Questi metodi permettono ai ricercatori di selezionare le distribuzioni a priori e di verosimiglianza in base a considerazioni teoriche, senza doversi preoccupare di altre restrizioni. Tuttavia, dal momento che questi metodi sono basati su calcoli computazionalmente intensivi, la stima numerica della funzione a posteriori MCMC può essere effettuata solo tramite software.

32.2.1. Integrazione di Monte Carlo

Il termine Monte Carlo si riferisce al fatto che la computazione fa ricorso ad un ripetuto campionamento casuale attraverso la generazione di sequenze di numeri casuali. Una delle sue applicazioni più potenti è il calcolo degli integrali mediante simulazione numerica. Un’illustrazione è fornita dal seguente esempio. Supponiamo di essere in grado di estrarre campioni casuali dalla distribuzione continua \(p(\theta \mid y)\) di media \(\mu\). Se possiamo ottenere una sequenza di realizzazioni indipendenti

\[ \theta^{(1)}, \theta^{(2)},\dots, \theta^{(T)} \overset{\text{iid}}{\sim} p(\theta \mid y) \]

allora diventa possibile calcolare

\[ \mathbb{E}(\theta \mid y) = \int \theta p(\theta \mid y) \,\operatorname {d}\!\theta \approx \frac{1}{T} \sum_{i=1}^T \theta^{(t)}. \]

In altre parole, l’aspettazione teorica di \(\theta\) può essere approssimata dalla media campionaria di un insieme di realizzazioni indipendenti ricavate da \(p(\theta \mid y)\). Per la Legge Forte dei Grandi Numeri, l’approssimazione diventa arbitrariamente esatta per \(T \rightarrow \infty\).2

Quello che è stato detto sopra non è altro che un modo sofisticato per dire che, se vogliamo calcolare un’approssimazione del valore atteso di una variabile casuale, non dobbiamo fare altro che la media aritmetica di un grande numero di realizzazioni indipendenti della variabile casuale. Come è facile intuire, l’approssimazione migliora al crescere del numero dei dati che abbiamo a disposizione.

Un’altra importante funzione di \(\theta\) è la funzione indicatore, \(I(l < \theta < u)\), che assume valore 1 se \(\theta\) giace nell’intervallo \((l, u)\) e 0 altrimenti. Il valore di aspettazione di \(I(l < \theta < u)\) rispetto a \(p(\theta)\) dà la probabilità che \(\theta\) rientri nell’intervallo specificato, \(Pr(l < \theta < u)\). Anche questa probabilità può essere approssimato usando l’integrazione Monte Carlo, ovvero prendendo la media campionaria del valore della funzione indicatore per ogni realizzazione \(\theta^{(t)}\). È semplice vedere come

\[ Pr(l < \theta < u) \approx \frac{\text{numero di realizzazioni } \theta^{(t)} \in (l, u)}{T}. \]

Abbiamo fornito qui alcuni accenni relativi all’integrazione di Monte Carlo perché, nell’analisi bayesiana, il metodo Monte Carlo viene usato per ottenere un’approssimazione della distribuzione a posteriori, quando tale distribuzione non può essere calcolata con metodi analitici. In altre parole, il metodo Monte Carlo consente di ottenere un gran numero di valori \(\theta\) che, nelle circostanze ideali, avrà una distribuzione identica alla distribuzione a posteriori \(p(\theta \mid y)\).

32.2.2. Campionamento dalla distribuzione a posteriori

Poniamoci ora il problema di approssimare la distribuzione a posteriori con una simulazione. Consideriamo nuovamente i dati di Zetsche et al. [ZBR19] (ovvero, 23 “successi” in 30 prove Bernoulliane) e, come in precedenza, assumiamo per \(\theta\) una distribuzione a priori \(Beta(2, 10)\). In tali circostanze, la distribuzione a posteriori può essere ottenuta analiticamente tramite lo schema beta-binomiale ed è una \(Beta(25, 17)\). Se vogliamo conoscere il valore della media a posteriori di \(\theta\), il risultato esatto è

\[ \bar{\theta}_{post} = \frac{\alpha}{\alpha + \beta} = \frac{25}{25 + 17} \approx 0.5952. \]

È anche possibile ottenere il valore della media a posteriori con una simulazione numerica. Conoscendo la forma della la distribuzione a posteriori, possiamo estrarre un campione di osservazioni da una \(Beta(25, 17)\) per poi calcolare la media delle osservazioni ottenute. Con poche osservazioni (diciamo 10) otteniamo un risultato molto approssimato.

y = beta(25, 17).rvs(10)
print(*y)

0.5855712504312496 0.509878192882081 0.6456408217722712 0.5897668794847047 0.5965134723322757 0.7476491089341565 0.5812615722016743 0.5012319567983722 0.6134085241985762 0.6577785364376901

y.mean()

0.6028700315473052

L’approssimazione migliora all’aumentare del numero di osservazioni.

beta(25, 17).rvs(100000).mean()

0.5951732534717287

Lo stesso si può dire delle altre statistiche descrittive: moda, varianza, eccetera.

Questa simulazione, detta di Monte Carlo, produce il risultato desiderato perché

• sappiamo che la distribuzione a posteriori è una \(Beta(25, 17)\),

• è possibile usare le funzioni Python per estrarre campioni casuali da una tale distribuzione.

Tuttavia, capita raramente di usare una distribuzione a priori coniugata alla verosimiglianza. Quindi, in generale, le due condizioni descritte sopra non si applicano. Ad esempio, nel caso di una verosimiglianza binomiale e di una distribuzione a priori gaussiana, la distribuzione a posteriori di \(\theta\) è

\[ p(\theta \mid y) = \frac{\mathrm{e}^{-(\theta - 1 / 2)^2} \theta^y (1 - \theta)^{n - y}} {\int_0^1 \mathrm{e}^{-(t - 1 / 2)^2} t^y (1 - t)^{n - y} dt}. \]

Una tale distribuzione non è implementata in Python; dunque non possiamo usare Python per ottenere campioni casuali da una tale distribuzione.

In tali circostanze, però, è possibile ottenere ottenere un campione causale dalla distribuzione a posteriori procedendo in un altro modo. Questo risultato si ottiene utilizzando i metodi Monte Carlo basati su Catena di Markov (MCMC). I metodi MCMC, di cui l’algoritmo Metropolis è un caso particolare e ne rappresenta il primo esempio, sono una classe di algoritmi che consentono di ottenere campioni casuali da una distribuzione a posteriori senza dovere conoscere la rappresentazione analitica di una tale distribuzione.3 Le tecniche MCMC sono il metodo computazionale maggiormente usato per risolvere i problemi dell’inferenza bayesiana.

32.3. L’algoritmo di Metropolis

Gli algoritmi Markov Chain Monte Carlo (MCMC) sono utilizzati per campionare la distribuzione a posteriori mediante una combinazione di tecniche “Monte Carlo” e “salti” intelligenti, che non dipendono dalla posizione iniziale. Questo approccio consente di effettuare ricerche “senza memoria” con salti intelligenti per evitare distorsioni sistematiche.

Uno degli algoritmi MCMC più noti è l’algoritmo Metropolis [MRR+53], che segue il seguente schema:

1. Iniziare l’algoritmo nella posizione corrente dello spazio dei parametri.

2. Proporre un salto in una nuova posizione nello spazio dei parametri.

3. Accettare o rifiutare il salto in modo probabilistico, utilizzando le informazioni precedenti e i dati disponibili.

4. Se il salto viene accettato, spostarsi nella nuova posizione e tornare al passaggio 1.

5. Se il salto viene rifiutato, restare nell’attuale posizione e tornare al passaggio 1.

6. Dopo aver effettuato un numero sufficiente di salti, restituire tutte le posizioni accettate come campioni dalla distribuzione a posteriori.

In questo post (https://elevanth.org/blog/2017/11/28/build-a-better-markov-chain/), è possibile vedere una rappresentazione grafica del processo di “esplorazione” dello spazio dei parametri dell’algoritmo Metropolis. La principale differenza tra i vari algoritmi MCMC sta nel modo in cui vengono effettuati i salti e nel modo in cui viene presa la decisione se saltare o meno.

Esaminiamo più in dettaglio l’algoritmo Metropolis.

• Si inizia con un punto arbitrario \(\theta^{(1)}\); quindi il primo valore \(\theta^{(1)}\) della catena di Markov può corrispondere semplicemente ad un valore a caso tra i valori possibili del parametro.

• Per ogni passo successivo della catena, \(m + 1\), si estrae un valore candidato \(\theta'\) da una distribuzione proposta: \(\theta' \sim \Pi(\theta)\). La distribuzione proposta può essere qualunque distribuzione, anche se, idealmente, è meglio che sia simile alla distribuzione a posteriori. In pratica, però, la distribuzione a posteriori è sconosciuta e quindi il valore \(\theta'\) viene estratto a caso da una qualche distribuzione simmetrica centrata sul valore corrente \(\theta^{(m)}\) del parametro. Nell’esempio presente useremo la gaussiana quale distribuzione proposta. La distribuzione proposta gaussiana sarà centrata sul valore corrente della catena e avrà una deviazione standard appropriata: \(\theta' \sim \mathcal{N}(\theta^{(m)}, \sigma)\). In pratica, questo significa che, se \(\sigma\) è piccola, il valore candidato \(\theta'\) sarà simile al valore corrente \(\theta^{(m)}\).

• Si calcola il rapporto \(r\) tra la densità a posteriori del parametro proposto \(\theta'\) e la densità a posteriori del parametro corrente \(\theta^{(m)}\). Si noti che, utilizzando la regola di Bayes, l’eq. (32.1) cancella la costante di normalizzazione, \(p(Y)\), dal rapporto. Il lato destro di quest’ultima uguaglianza contiene solo le verosimiglianze e le distribuzioni a priori, entrambe facilmente calcolabili.

(32.1)\[ r = \frac{p(\theta' \mid y)}{p(\theta^{(m)} \mid y)} = \frac{\frac{p(y \mid \theta') p(\theta')}{p(Y)}}{\frac{p(y \mid \theta^{(m)}) p(\theta^{(m)})}{p(Y)}} = \frac{p(y \mid \theta') p(\theta')}{p(y \mid \theta^{(m)}) p(\theta^{(m)})}. \]

• Si decide se accettare il candidato \(\theta'\) oppure se rigettarlo e estrarre un nuovo valore dalla distribuzione proposta. Possiamo pensare al rapporto \(r\) come alla risposta alla seguente domanda: alla luce dei dati, quale stima di \(\theta\) è più credibile, il valore candidato o il valore corrente? Se \(r\) è maggiore di 1, ciò significa che il candidato è più credibile del valore corrente; dunque se \(r\) è maggiore di 1 il candidato viene sempre accettato. Altrimenti, si decide di accettare il candidato con una probabilità minore di 1, ovvero non sempre, ma soltanto con una probabilità uguale ad \(r\). Se \(r\) è uguale a 0.10, ad esempio, questo significa che la credibilità a posteriori del valore candidato è 10 volte più piccola della credibilità a posteriori del valore corrente. Dunque, il valore candidato verrà accettato solo nel 10% dei casi. Come conseguenza di questa strategia di scelta, l’algoritmo Metropolis ottiene un campione casuale dalla distribuzione a posteriori, dato che la probabilità di accettare il valore candidato è proporzionale alla densità del candidato nella distribuzione a posteriori. Dal punto di vista algoritmico, tale procedura viene implementata confrontando il rapporto \(r\) con un valore estratto a caso da una distribuzione uniforme \(Unif(0, 1)\). Se \(r > u \sim Unif(0, 1)\), allora il candidato \(\theta'\) viene accettato e la catena si muove in quella nuova posizione, ovvero \(\theta^{(m+1)} = \theta'\). Altrimenti \(\theta^{(m+1)} = \theta^{(m)}\) e si estrae un nuovo candidato dalla distribuzione proposta.

• Il passaggio finale dell’algoritmo calcola l’accettanza in una specifica esecuzione dell’algoritmo, ovvero la proporzione di candidati \(\theta'\) che sono stati accettati quali valori successivi della catena.

L’algoritmo Metropolis prende come input il numero \(T\) di passi da simulare, la deviazione standard \(\sigma\) della distribuzione proposta e la densità a priori, e ritorna come output la sequenza \(\theta^{(1)}, \theta^{(2)}, \dots, \theta^{(T)}\). La chiave del successo dell’algoritmo Metropolis è il numero di passi fino a che la catena approssima la stazionarietà. Tipicamente i primi da 1000 a 5000 elementi sono scartati. Dopo un certo periodo \(k\) (detto di burn-in), la catena di Markov converge ad una variabile casuale che è distribuita secondo la distribuzione a posteriori (stazionarietà). In altre parole, i campioni del vettore \(\left(\theta^{(k+1)}, \theta^{(k+2)}, \dots, \theta^{(T)}\right)\) diventano campioni di \(p(\theta \mid y)\).

32.3.1. Un’applicazione empirica

Implementiamo ora l’algoritmo Metropolis per trovare la distribuzione a posteriori di \(\theta\) per i dati di Zetsche et al. [ZBR19] (23 successi in 30 prove Bernoulliane), imponendo su \(\theta\) una \(Beta(2, 10)\). Nell’implementazione che verrà qui presentata, l’algoritmo Metropolis richiede l’uso delle seguenti funzioni.

Verosimiglianza. Useremo una funzione di verosimiglianza binomiale.

def get_likelihood(p):
    k = 23
    n = 30
    return binom.pmf(k, n, p)

Distribuzione a priori. In questo esempio, la distribuzione a priori è una distribuzione Beta con parametri 2 e 10, che viene scelta solo per motivi didattici e non ha alcuna motivazione ulteriore.

def get_prior(p):
    a = 2
    b = 10
    return beta.pdf(p, a, b)

Distribuzione a posteriori. La distribuzione a posteriori è data dal prodotto della distribuzione a priori e della verosimiglianza. Si noti che, per il motivo spiegato prima, non è necessario normalizzare la distribuzione a posteriori.

def get_posterior(p):
    return get_likelihood(p) * get_prior(p)

Distribuzione proposta. Per implementare l’algoritmo Metropolis utilizzeremo una distribuzione proposta gaussiana con parametro \(\sigma\) = 0.9. Il valore candidato sarà dunque un valore selezionato a caso da una gaussiana di parametri \(\mu\) uguale al valore corrente nella catena e \(\sigma = 0.9\). In questo esempio, la deviazione standard \(\sigma\) è stata scelta empiricamente in modo tale da ottenere una accettanza adeguata. L’accettanza ottimale è pari a circa 0.20/0.30 — se l’accettanza è troppo grande, l’algoritmo esplora uno spazio troppo ristretto della distribuzione a posteriori.4 Nella funzione ho anche inserito un controllo che impone al valore candidato di essere incluso nell’intervallo [0, 1], com’è necessario per il valore di una proporzione.5

def get_proposal(p_current, proposal_width):
    while 1:
        proposal = norm(p_current, proposal_width).rvs()
        if proposal > 0 and proposal < 1:
            break
    return proposal

L’algoritmo Metropolis viene implementato nella funzione seguente.

def sampler(samples=100, p_init=0.5, proposal_width=0.1):
    p_current = p_init
    posterior = [p_current]
    acceptance = 0
    for i in range(samples):
        # Suggest new position
        proposal = get_proposal(p_current, proposal_width)
        # Accept proposal?
        p_accept = get_posterior(proposal) / get_posterior(p_current)
        accept = np.random.rand() < p_accept
        if accept:
            # Update position
            p_current = proposal
            acceptance = acceptance + 1
        posterior.append(p_current)
    return acceptance / samples, np.array(posterior)

Utilizzo ora il campionatore sampler(), per generare una sequenza (catena) di valori \(\theta\).

acceptance, posterior = sampler(samples=20000, p_init=0.5, proposal_width=0.9)

---------------------------------------------------------------------------
KeyboardInterrupt                         Traceback (most recent call last)
Cell In[13], line 1
----> 1 acceptance, posterior = sampler(samples=20000, p_init=0.5, proposal_width=0.9)

Cell In[12], line 7, in sampler(samples, p_init, proposal_width)
      4 acceptance = 0
      5 for i in range(samples):
      6     # Suggest new position
----> 7     proposal = get_proposal(p_current, proposal_width)
      8     # Accept proposal?
      9     p_accept = get_posterior(proposal) / get_posterior(p_current)

Cell In[11], line 3, in get_proposal(p_current, proposal_width)
      1 def get_proposal(p_current, proposal_width):
      2     while 1:
----> 3         proposal = norm(p_current, proposal_width).rvs()
      4         if proposal > 0 and proposal < 1:
      5             break

File ~/mambaforge/envs/pymc_env/lib/python3.11/site-packages/scipy/stats/_distn_infrastructure.py:829, in rv_generic.__call__(self, *args, **kwds)
    828 def __call__(self, *args, **kwds):
--> 829     return self.freeze(*args, **kwds)

File ~/mambaforge/envs/pymc_env/lib/python3.11/site-packages/scipy/stats/_distn_infrastructure.py:824, in rv_generic.freeze(self, *args, **kwds)
    809 """Freeze the distribution for the given arguments.
    810 
    811 Parameters
   (...)
    821 
    822 """
    823 if isinstance(self, rv_continuous):
--> 824     return rv_continuous_frozen(self, *args, **kwds)
    825 else:
    826     return rv_discrete_frozen(self, *args, **kwds)

File ~/mambaforge/envs/pymc_env/lib/python3.11/site-packages/scipy/stats/_distn_infrastructure.py:440, in rv_frozen.__init__(self, dist, *args, **kwds)
    437 self.kwds = kwds
    439 # create a new instance
--> 440 self.dist = dist.__class__(**dist._updated_ctor_param())
    442 shapes, _, _ = self.dist._parse_args(*args, **kwds)
    443 self.a, self.b = self.dist._get_support(*shapes)

File ~/mambaforge/envs/pymc_env/lib/python3.11/site-packages/scipy/stats/_distn_infrastructure.py:1936, in rv_continuous.__init__(self, momtype, a, b, xtol, badvalue, name, longname, shapes, extradoc, seed)
   1931 self.extradoc = extradoc
   1933 self._construct_argparser(meths_to_inspect=[self._pdf, self._cdf],
   1934                           locscale_in='loc=0, scale=1',
   1935                           locscale_out='loc, scale')
-> 1936 self._attach_methods()
   1938 if longname is None:
   1939     if name[0] in ['aeiouAEIOU']:

File ~/mambaforge/envs/pymc_env/lib/python3.11/site-packages/scipy/stats/_distn_infrastructure.py:1971, in rv_continuous._attach_methods(self)
   1967 """
   1968 Attaches dynamically created methods to the rv_continuous instance.
   1969 """
   1970 # _attach_methods is responsible for calling _attach_argparser_methods
-> 1971 self._attach_argparser_methods()
   1973 # nin correction
   1974 self._ppfvec = vectorize(self._ppf_single, otypes='d')

File ~/mambaforge/envs/pymc_env/lib/python3.11/site-packages/scipy/stats/_distn_infrastructure.py:669, in rv_generic._attach_argparser_methods(self)
    661 """
    662 Generates the argument-parsing functions dynamically and attaches
    663 them to the instance.
   (...)
    666 during unpickling (__setstate__)
    667 """
    668 ns = {}
--> 669 exec(self._parse_arg_template, ns)
    670 # NB: attach to the instance, not class
    671 for name in ['_parse_args', '_parse_args_stats', '_parse_args_rvs']:

File <string>:0

KeyboardInterrupt: 

Esamino l’accettanza.

acceptance

0.25335

Il valore trovato conferma la bontà della deviazione standard (\(\sigma\) = 0.9) scelta per la distribuzione proposta.

La lista posterior contiene 20,000 valori di una catena di Markov. Escludo i primi 5000 valori considerati come burn-in e considero i restanti 15,000 valori come un campione casuale estratto dalla distribuzione a posteriori \(p(\theta \mid y)\).

Mediante i valori della catena così ottenuta è facile trovare una stima a posteriori del parametro \(\theta\). Per esempio, posso trovare la stima della media a posteriori.

np.mean(posterior[5001:20000])

0.5945120988409726

Oppure posso calcolare la deviazione standard dell’approssimazione numerica della distribuzione a posteriori.

np.std(posterior[5001:20000])

0.07483958412295862

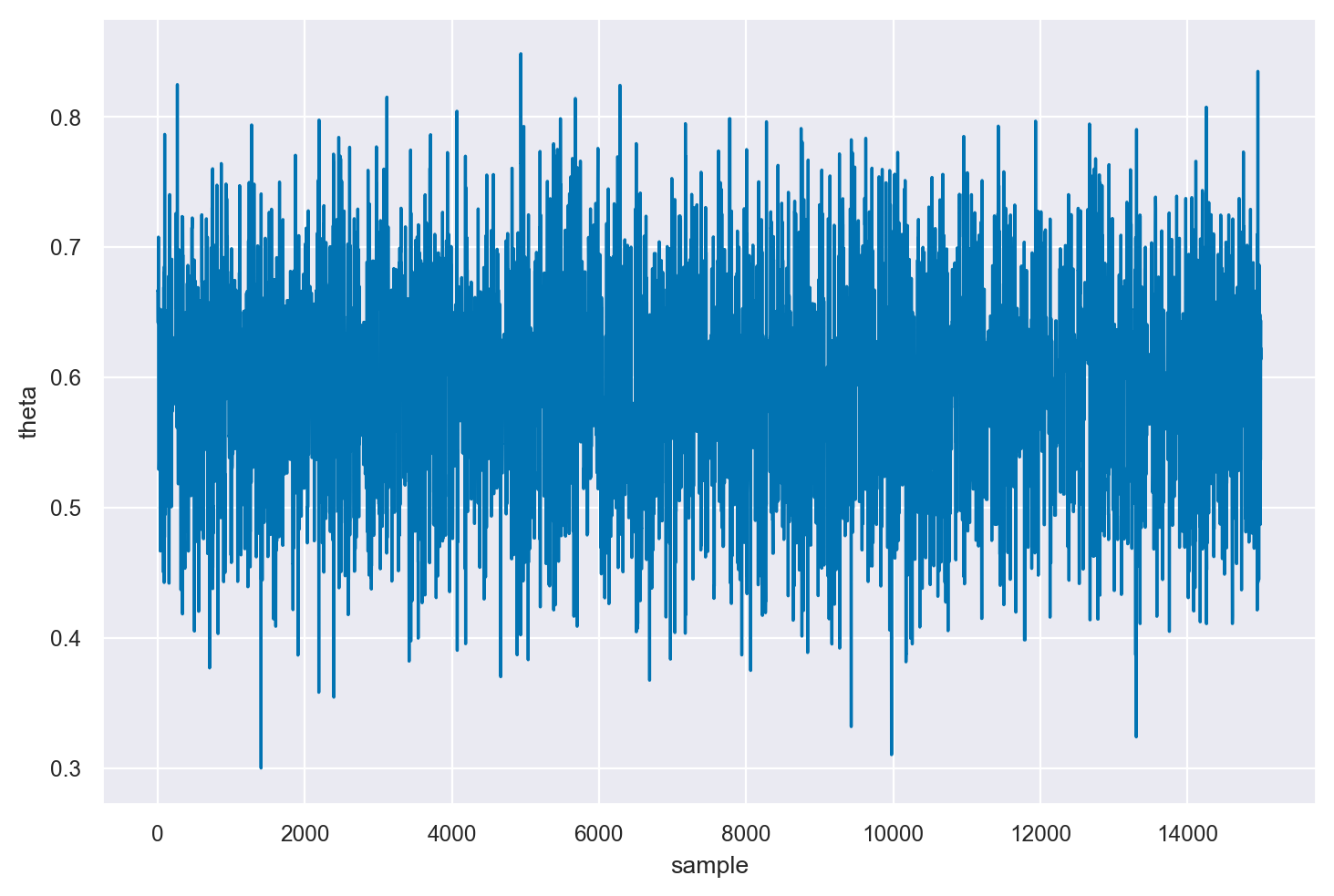
Visualizziamo un trace plot dei valori della catena di Markov.

fig, ax = plt.subplots()
ax.plot(posterior[5001:20000])
_ = ax.set(xlabel="sample", ylabel="theta")

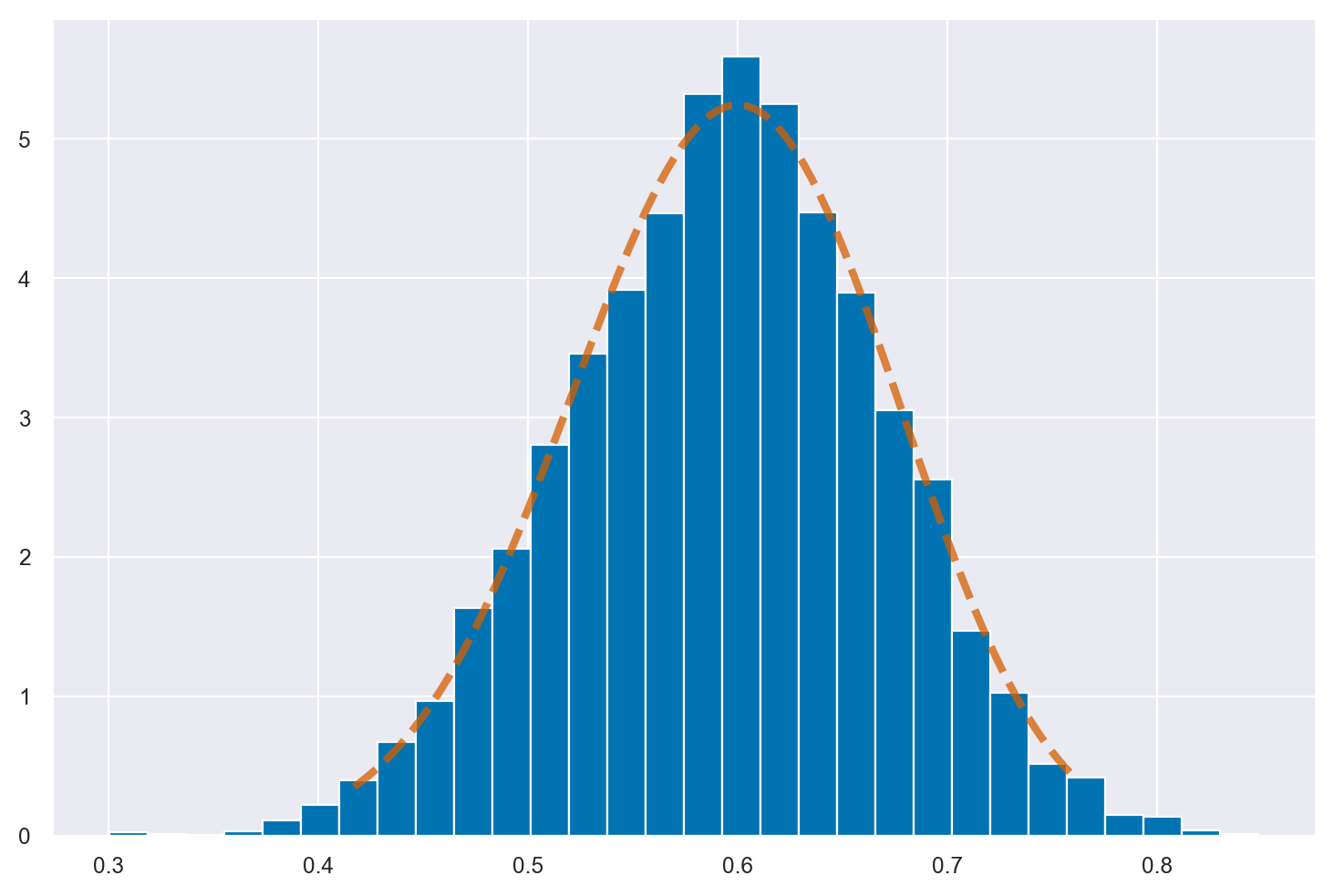
Nella figura, l’istogramma descrive i valori \(\theta\) prodotti dall’algoritmo Metropolis mentre la linea continua descrive la distribuzione a posteriori ottenuta per via analitica, ovvero una \(Beta(25, 17)\). La figura indica che la catena converge alla corretta distribuzione a posteriori.

plt.hist(posterior[5001:20000], bins=30, label="estimated posterior", density=True)

a = 25
b = 17
x = np.linspace(st.beta.ppf(0.01, a, b), st.beta.ppf(0.99, a, b), 100)
_ = plt.plot(x, st.beta.pdf(x, a, b), "r--", lw=3, alpha=0.75, label="Beta(25, 17)")

Uso la funzione summary di arviz per calolare l’intervallo di credibilità, ovvero l’intervallo che contiene la proporzione indicata dei valori estratti a caso dalla distribuzione a posteriori.

az.summary(posterior[5001:20000], kind="stats", hdi_prob=0.95, round_to=2)

	mean	sd	hdi_2.5%	hdi_97.5%
x	0.59	0.07	0.44	0.73

Un KDE plot corrispondente all’istogramma precedente si può generare usando az.plot_posterior(). La curva rappresenta l’intera distribuzione a posteriori e viene calcolata utilizzando la stima della densità del kernel (KDE) che serve a “lisciare” l’istogramma.

_ = az.plot_posterior(posterior[5001:20000])

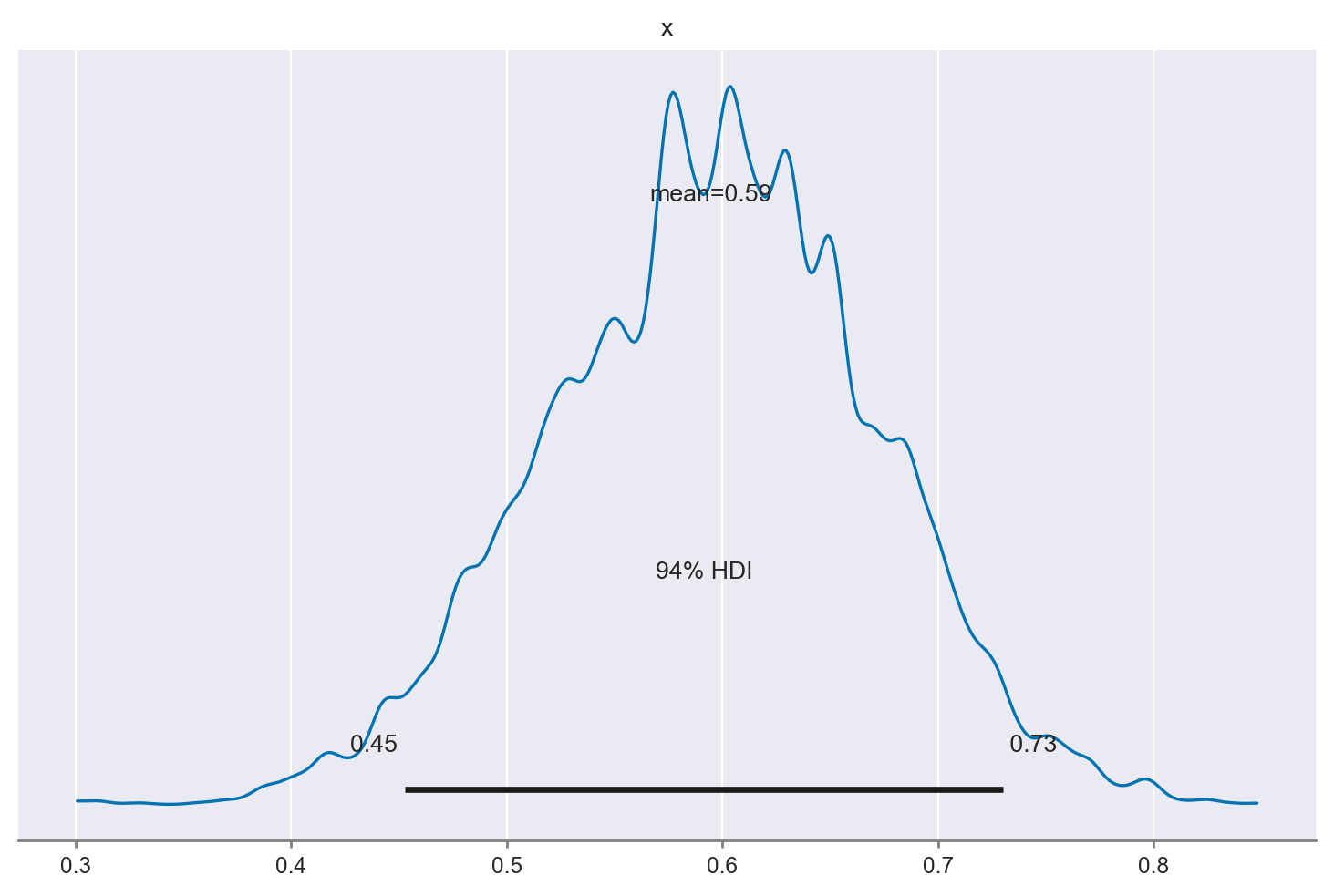
L’HDI è una scelta comune nelle statistiche bayesiane e valori arrotondati come 50% o 95% sono molto popolari. Ma ArviZ utilizza il 94% come valore predefinito, come mostrato nella figura precedente. La ragione di questa scelta è che il 94% è vicino al valore ampiamente utilizzato del 95%, ma è anche diverso da questo, così da servire da “amichevole promemoria” che non c’è niente di speciale nella soglia del 5%. Idealmente sarebbe opportuno scegliere un valore che si adatti alle specifiche esigenze dell’analisi statistica che si sta svolgendo, o almeno riconoscere che si sta usando un valore arbitrario.

L’algoritmo descritto in questo capitolo è di Metropolis et al. [MRR+53]. Un miglioramento di Hastings [Has70] ha portato all’algoritmo Metropolis-Hastings. Il campionatore di Gibbs è dovuto a [GG84]. L’approccio hamiltoniano Monte Carlo è dovuto a Duane et al. [DKPR87] e il No-U-Turn Sampler (NUTS) è dovuto a Hoffman et al. [HG+14]. Un’introduzione matematicamente intuitiva all’algoritmo Metropolis è data da Kruschke [Kru14].

32.4. Diagnostiche della soluzione MCMC

In questo capitolo abbiamo illustrato l’esecuzione di una singola catena di Markov in cui si parte un unico valore iniziale e si raccolgono i valori simulati da molte iterazioni. È possibile però che i valori di una catena siano influenzati dalla scelta del valore iniziale. Quindi una raccomandazione generale è di eseguire l’algoritmo Metropolis più volte utilizzando diversi valori di partenza. In questo caso, si avranno più catene di Markov. Confrontando le proprietà delle diverse catene si esplora la sensibilità dell’inferenza alla scelta del valore di partenza. I software MCMC consentono sempre all’utente di specificare diversi valori di partenza e di generare molteplici catene di Markov.

32.4.1. Stazionarietà

Un punto importante da verificare è se il campionatore ha raggiunto la sua distribuzione stazionaria. La convergenza di una catena di Markov alla distribuzione stazionaria viene detta “mixing”.

32.4.1.1. Autocorrelazione

Informazioni sul “mixing” della catena di Markov sono fornite dall’autocorrelazione. L’autocorrelazione misura la correlazione tra i valori successivi di una catena di Markov. Il valore \(m\)-esimo della serie ordinata viene confrontato con un altro valore ritardato di una quantità \(k\) (dove \(k\) è l’entità del ritardo) per verificare quanto si correli al variare di \(k\). L’autocorrelazione di ordine 1 (lag 1) misura la correlazione tra valori successivi della catena di Markow (cioè, la correlazione tra \(\theta^{(m)}\) e \(\theta^{(m-1)}\)); l’autocorrelazione di ordine 2 (lag 2) misura la correlazione tra valori della catena di Markow separati da due “passi” (cioè, la correlazione tra \(\theta^{(m)}\) e \(\theta^{(m-2)}\)); e così via.

L’autocorrelazione di ordine \(k\) è data da \(\rho_k\) e può essere stimata come:

(32.2)\[\begin{split} \begin{align} \rho_k &= \frac{Cov(\theta_m, \theta_{m+k})}{Var(\theta_m)}\notag\\ &= \frac{\sum_{m=1}^{n-k}(\theta_m - \bar{\theta})(\theta_{m-k} - \bar{\theta})}{\sum_{m=1}^{n-k}(\theta_m - \bar{\theta})^2} \qquad\text{con }\quad \bar{\theta} = \frac{1}{n}\sum_{m=1}^{n}\theta_m. \end{align} \end{split}\]

Per fare un esempio pratico, simuliamo dei dati autocorrelati.

x = pd.array([22, 24, 25, 25, 28, 29, 34, 37, 40, 44, 51, 48, 47, 50, 51])
print(*x)

22 24 25 25 28 29 34 37 40 44 51 48 47 50 51

L’autocorrelazione di ordine 1 è semplicemente la correlazione tra ciascun elemento e quello successivo nella sequenza.

sm.tsa.acf(x)

array([ 1.        ,  0.83174224,  0.65632458,  0.49105012,  0.27863962,
        0.03102625, -0.16527446, -0.30369928, -0.40095465, -0.45823389,
       -0.45047733, -0.36933174])

Nell’esempio, il vettore x è una sequenza temporale di 15 elementi. Il vettore \(x'\) include gli elementi con gli indici da 0 a 13 nella sequenza originaria, mentre il vettore \(x''\) include gli elementi 1:14. Gli elementi delle coppie ordinate dei due vettori avranno dunque gli indici \((0, 1)\), \((1, 2), (2, 3), \dots (13, 14)\) degli elementi della sequenza originaria. La correlazione di Pearson tra i vettori \(x'\) e \(x''\) corrisponde all’autocorrelazione di ordine 1 della serie temporale.

Nell’output precedente

• 0.83174224 è l’autocorrelazione di ordine 1 (lag = 1),

• 0.65632458 è l’autocorrelazione di ordine 2 (lag = 2),

• 0.49105012 è l’autocorrelazione di ordine 3 (lag = 3),

• ecc.

È possibile specificare il numero di ritardi (lag) da utilizzare con l’argomento nlags:

sm.tsa.acf(x, nlags=4)

array([1.        , 0.83174224, 0.65632458, 0.49105012, 0.27863962])

In Python possiamo creare un grafico della funzione di autocorrelazione (correlogramma) per una serie temporale usando la funzione tsaplots.plot_acf() dalla libreria statsmodels.

_ = tsaplots.plot_acf(x, lags=9)

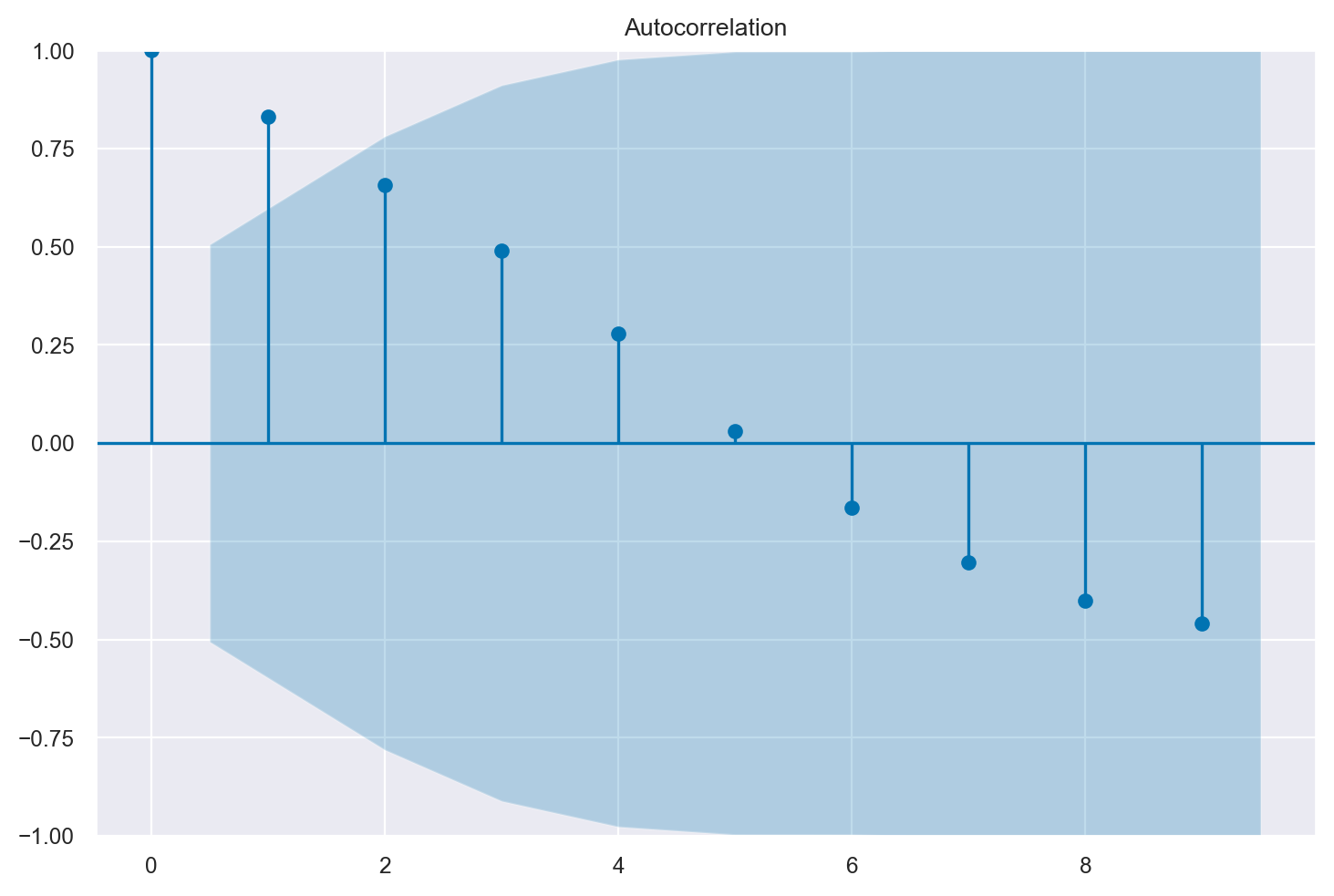
Il correlogramma è uno strumento grafico usato per la valutazione della tendenza di una catena di Markov nel tempo. Il correlogramma si costruisce a partire dall’autocorrelazione \(\rho_k\) di una catena di Markov in funzione del ritardo \(k\) con cui l’autocorrelazione è calcolata: nel grafico ogni barretta verticale riporta il valore dell’autocorrelazione (sull’asse delle ordinate) in funzione del ritardo (sull’asse delle ascisse).

In situazioni ottimali l’autocorrelazione diminuisce rapidamente ed è effettivamente pari a 0 per piccoli lag. Ciò indica che i valori della catena di Markov che si trovano a più di soli pochi passi di distanza gli uni dagli altri non risultano associati tra loro, il che fornisce una conferma del “mixing” della catena di Markov, ossia della convergenza alla distribuzione stazionaria. Nelle analisi bayesiane, una delle strategie che consentono di ridurre l’autocorrelazione è quella di assottigliare l’output immagazzinando solo ogni \(m\)-esimo punto dopo il periodo di burn-in. Una tale strategia va sotto il nome di thinning.

32.4.2. Test di convergenza

Un test di convergenza può essere svolto in maniera grafica mediante le tracce delle serie temporali (trace plot), cioè il grafico dei valori simulati rispetto al numero di iterazioni. Se la catena è in uno stato stazionario le tracce mostrano assenza di periodicità nel tempo e ampiezza costante, senza tendenze visibili o andamenti degni di nota.

Ci sono inoltre alcuni test che permettono di verificare la stazionarietà del campionatore dopo un dato punto. Uno è il test di Geweke che suddivide il campione, dopo aver rimosso un periodo di burn in, in due parti. Se la catena è in uno stato stazionario, le medie dei due campioni dovrebbero essere uguali. Un test modificato, chiamato Geweke z-score, utilizza un test \(z\) per confrontare i due subcampioni ed il risultante test statistico, se ad esempio è più alto di 2, indica che la media della serie sta ancora muovendosi da un punto ad un altro e quindi è necessario un periodo di burn-in più lungo.

32.5. Commenti e considerazioni finali

In generale, la distribuzione a posteriori dei parametri di un modello statistico non può essere determinata per via analitica. Tale problema viene invece affrontato facendo ricorso ad una classe di algoritmi per il campionamento da distribuzioni di probabilità che sono estremamente onerosi dal punto di vista computazionale e che possono essere utilizzati nelle applicazioni pratiche solo grazie alla potenza di calcolo dei moderni computer. Lo sviluppo di software che rendono sempre più semplice l’uso dei metodi MCMC, insieme all’incremento della potenza di calcolo dei computer, ha contribuito a rendere sempre più popolare il metodo dell’inferenza bayesiana che, in questo modo, può essere estesa a problemi di qualunque grado di complessità.

32.6. Watermark

%load_ext watermark
%watermark -n -u -v -iv -w

Last updated: Sat May 06 2023

Python implementation: CPython
Python version       : 3.11.3
IPython version      : 8.13.2

seaborn    : 0.12.2
scipy      : 1.10.1
matplotlib : 3.7.1
arviz      : 0.15.1
statsmodels: 0.14.0
pandas     : 1.5.3
numpy      : 1.23.5

Watermark: 2.3.1

---

1

Per comprendere la maledizione della dimensionalità, possiamo considerare l’esempio di una griglia di 100 punti equispaziati. Nel caso di un solo parametro, sarebbe necessario calcolare solo 100 valori. Tuttavia, se abbiamo due parametri, il numero di valori da calcolare diventa \(100^2\). Se invece abbiamo 10 parametri, il numero di valori da calcolare sarebbe di \(10^{10}\). È evidente che la quantità di calcoli richiesta diventa troppo grande persino per un computer molto potente. Pertanto, per modelli che richiedono la stima di un numero significativo di parametri, è necessario utilizzare un approccio diverso.

2

L’integrazione Monte Carlo può essere utilizzata anche per la valutazione di integrali più complessi.

3

In termini più formali, si può dire che i metodi MCMC consentono di costruire sequenze di punti (detti catene di Markov) nello spazio dei parametri le cui densità sono proporzionali alla distribuzione a posteriori. In altre parole, dopo aver simulato un grande numero di passi della catena si possono usare i valori così generati come se fossero un campione casuale della distribuzione a posteriori. Un’introduzione alle catene di Markov è fornita in Appendice.

4

L’accettanza dipende dalla distribuzione proposta: in generale, tanto più la distribuzione proposta è simile alla distribuzione target, tanto più alta diventa l’accettanza.

5

Si possono trovare implementazioni più eleganti di quella presentata qui. Il presente esercizio ha solo lo scopo di illustrare la logica soggiacente all’algoritmo Metropolis; non ci preoccupiamo di trovare un’implementazione efficente dell’algoritmo.