18. Probabilità condizionata#
In questo capitolo esploreremo i seguenti concetti probabilistici:
La probabilità congiunta, ovvero la probabilità del verificarsi simultaneo di due eventi che appartengono allo stesso evento, anche se si verificano in momenti diversi. Ad esempio, potremmo essere interessati alla probabilità congiunta di estrarre una pallina rossa e una verde.
La probabilità marginale, ovvero la probabilità di un singolo evento indipendentemente da tutti gli altri eventi. Ad esempio, possiamo calcolare la probabilità marginale di estrarre una pallina verde da un’urna.
La probabilità condizionata, ovvero la probabilità di un evento dato il verificarsi di un altro evento. Ad esempio, se estraiamo una pallina verde da un’urna, possiamo chiederci quanto è grande la probabilità di estrarre una seconda pallina verde dalla stessa urna.
Inoltre, esamineremo i principali teoremi associati alla probabilità condizionata.
18.1. Il paradosso di Monty Hall#
Il paradosso di Monty Hall è un esempio molto interessante di come la conoscenza di nuove informazioni possa portare a una rivalutazione dei termini del problema “condizionatamente alle informazioni acquisite”. Questo famoso problema di teoria della probabilità è legato al noto gioco a premi statunitense “Let’s Make a Deal”, e prende il nome dal conduttore dello show, Monte Halprin, conosciuto con lo pseudonimo di Monty Hall.

Il gioco consiste nel mostrare al concorrente tre porte chiuse, dietro una delle quali si trova un’automobile, mentre dietro le altre due porte si nasconde una capra ciascuna. Il concorrente sceglie una porta, senza aprirla, e poi Monty Hall apre una delle altre due porte, rivelando una delle due capre. A questo punto, Monty offre al concorrente la possibilità di cambiare la propria scelta iniziale, passando all’unica porta restante. Il paradosso deriva dal fatto che cambiare la porta migliora le probabilità del concorrente di vincere l’automobile, portandole da 1/3 a 2/3.
Per dimostrare questo paradosso, possiamo scrivere una simulazione in Python in cui immaginiamo due scenari, ripetuti migliaia di volte: uno in cui il concorrente rimane con la sua scelta iniziale e uno in cui il concorrente cambia la propria scelta dopo che Monty Hall ha aperto una porta dietro la quale si nascondeva una capra.
Riporto qui sotto lo script della simulazione eseguita da un gruppo di studenti di Psicometria A.A. 2022-2023.
import numpy as np
import pandas as pd
import random
porte = [
"capra1",
"capra2",
"macchina",
] # definisco il gioco, scelgo una porta a caso per n volte
counter = 0
contatore_cambio = 0
n = 10000
porta_vincente = "macchina"
for i in range(n):
scelta_casuale = random.choice(porte)
porte_rimaste = [x for x in porte if x != scelta_casuale]
porta_rivelata = random.choice([x for x in porte_rimaste if x != porta_vincente])
porta_alternativa = [
x for x in porte if x != scelta_casuale and x != porta_rivelata
]
if "macchina" in porta_alternativa:
contatore_cambio += 1
if scelta_casuale == "macchina":
counter += 1
print(counter / n) # quante volte vinco non cambiando porta
print(contatore_cambio / n) # quante volte vinco cambiando porta
0.3314
0.6686
18.2. Probabilità condizionata su altri eventi#
L’attribuzione di una probabilità ad un evento è sempre condizionata dalle conoscenze che abbiamo a disposizione. Per un determinato stato di conoscenze, attribuiamo ad un dato evento una certa probabilità di verificarsi; ma se il nostro stato di conoscenze cambia, allora cambierà anche la probabilità che attribuiremo all’evento in questione. Infatti, si può pensare che tutte le probabilità siano probabilità condizionate, anche se l’evento condizionante non è sempre esplicitamente menzionato. Arriviamo così alla seguente definizione.
Definizione
Siano \(A\) e \(B\) due eventi definiti sullo spazio campione \(S\). Supponiamo di sapere che l’evento \(B\) si è verificato. Si chiama probabilità condizionata di \(A\) dato \(B\) il numero
dove \(P(A\cap B)\) è la probabilità congiunta dei due eventi, ovvero la probabilità che si verifichino entrambi.
Si noti che \(P(A \mid B)\) non è definita se \(P(B) = 0\).
Possiamo pensare alla probabilità condizionata come a un cambiamento dello spazio campionario da \(S\) a \(B\). Per semplici spazi campione abbiamo dunque
Consideriamo un esempio. Sappiamo che la somma del lancio di due dadi ha prodotto un risultato dispari. Qual è la probabilità che la somma sia minore di 8?
r = range(1, 7)
sample = [(i, j) for i in r for j in r]
sample_odd = [roll for roll in sample if (sum(roll) % 2) != 0]
sample_odd
[(1, 2),
(1, 4),
(1, 6),
(2, 1),
(2, 3),
(2, 5),
(3, 2),
(3, 4),
(3, 6),
(4, 1),
(4, 3),
(4, 5),
(5, 2),
(5, 4),
(5, 6),
(6, 1),
(6, 3),
(6, 5)]
event = [roll for roll in sample_odd if sum(roll) < 8]
print(f"{len(event)} / {len(sample_odd)}")
12 / 18
Se applichiamo l’eq. (18.1), abbiamo: \(P(A \cap B)\) = 12/36, \(P(B)\) = 18/36 e
18.2.1. Mammografia e cancro al seno#
Consideriamo un altro esempio. Supponiamo che lo screening per la diagnosi precoce del tumore mammario si avvalga di un test che è accurato al 90%, nel senso che classifica correttamente il 90% delle donne colpite dal cancro e il 90% delle donne che non hanno il cancro al seno. Supponiamo che l’1% delle donne sottoposte allo screening abbia effettivamente il cancro al seno (e d’altra parte, il 99% non lo ha). Ci chiediamo: (1) qual è la probabilità che una donna scelta a caso ottenga una mammografia positiva, e (2) se la mammografia è positiva, qual è la probabilità che vi sia effettivamente un tumore al seno?
Per risolvere questo problema, supponiamo che il test in questione venga somministrato ad un grande campione di donne, diciamo a 1000 donne. Di queste 1000 donne, 10 (ovvero, l’1%) hanno il cancro al seno. Per queste 10 donne, il test darà un risultato positivo in 9 casi (ovvero, nel 90% dei casi). Per le rimanenti 990 donne che non hanno il cancro al seno, il test darà un risultato positivo in 99 casi (se la probabilità di un vero positivo è del 90%, la probabilità di un falso positivo è del 10%). Questa situazione è rappresentata nella figura seguente.
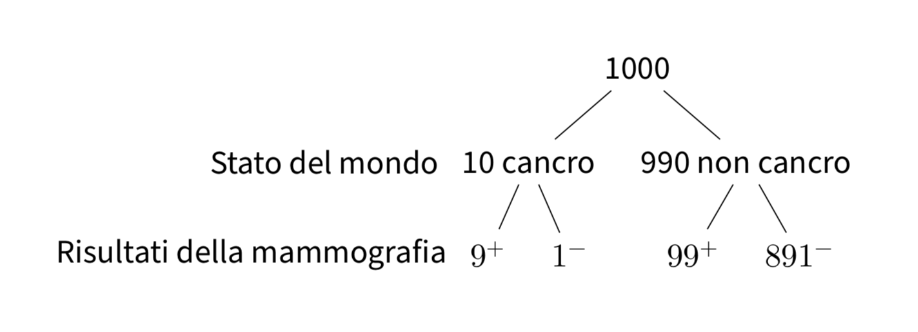
Combinando i due risultati precedenti, vediamo che il test dà un risultato positivo per 9 donne che hanno effettivamente il cancro al seno e per 99 donne che non ce l’hanno, per un totale di 108 risultati positivi. Dunque, la probabilità di ottenere un risultato positivo al test è \(\frac{108}{1000}\) = 11%. Ma delle 108 donne che hanno ottenuto un risultato positivo al test, solo 9 hanno il cancro al seno. Dunque, la probabilità di avere il cancro al seno, dato un risultato positivo al test (che ha le proprietà descritte sopra), è pari a \(\frac{9}{108}\) = 8%.
In questo esercizio, la probabilità dell’evento “ottenere un risultato positivo al test” è una probabilità non condizionata, mentre la probabilità dell’evento “avere il cancro al seno, dato che il test ha prodotto un risultato positivo” è una probabilità condizionata.
18.3. Teorema della probabilità composta#
È possibile scrivere l’eq. (18.1) nella forma:
Questo secondo modo di scrivere l’eq. (18.1) è chiamato teorema della probabilità composta (o regola moltiplicativa, o regola della catena). La legge della probabilità composta ci dice che la probabilità che si verifichino due eventi \(A\) e \(B\) è pari alla probabilità di uno dei due eventi moltiplicato con la probabilità dell’altro evento condizionato al verificarsi del primo.
L’eq. (18.2) si estende al caso di \(n\) eventi \(A_1, \dots, A_n\) nella forma seguente:
Per esempio, nel caso di quattro eventi abbiamo
Per fare un esempio, consideriamo il problema seguente. Da un’urna contenente 6 palline bianche e 4 nere si estrae una pallina per volta, senza reintrodurla nell’urna. Indichiamo con \(B_i\) l’evento: “esce una pallina bianca alla \(i\)-esima estrazione” e con \(N_i\) l’estrazione di una pallina nera. L’evento: “escono due palline bianche nelle prime due estrazioni” è rappresentato dalla intersezione \(\{B_1 \cap B_2\}\) e, per l’eq. (18.2), la sua probabilità vale
\(P(B_1)\) vale 6/10, perché nella prima estrazione \(\Omega\) è costituito da 10 elementi: 6 palline bianche e 4 nere. La probabilità condizionata \(P(B_2 \mid B_1)\) vale 5/9, perché nella seconda estrazione, se è verificato l’evento \(B_1\), lo spazio campionario consiste di 5 palline bianche e 4 nere. Si ricava pertanto:
In modo analogo si ha che
Se l’esperimento consiste nell’estrazione successiva di 3 palline, la probabilità che queste siano tutte bianche, per l’eq. (18.3), vale
La probabilità dell’estrazione di tre palline nere è invece:
18.4. Il teorema della probabilità totale#
Il teorema della probabilità totale (detto anche teorema delle partizioni) afferma che se abbiamo una partizione di uno spazio campionario \(\Omega\) in \(n\) eventi mutualmente esclusivi e tali che la loro unione formi \(\Omega\), allora la probabilità di un qualsiasi evento in \(\Omega\) può essere calcolata sommando la probabilità dell’evento su ciascun sottoinsieme della partizione pesata in base alla probabilità del sottoinsieme.
In altre parole, se \(H_1, H_2, \dots, H_n\) sono eventi mutualmente esclusivi e tali che \(\bigcup_{i=1}^n H_i = \Omega\), allora per ogni evento \(E \subseteq \Omega\), la probabilità di \(E\) è data da:
dove \(P(E \mid H_i)\) è la probabilità condizionata di \(E\) dato che si è verificato \(H_i\) r \(P(H_i)\) è la probabilità dell’evento \(H_i\).
Il caso più semplice è quello di una partizione dello spazio campione in due sottoinsiemi: \(P(E) = P(E \cap H_1) + P(E \cap H_2)\).
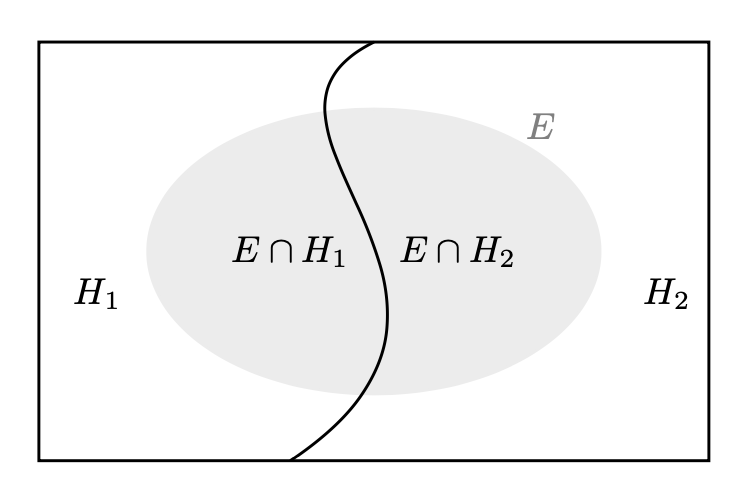
In tali circostanza abbiamo che
L’eq. (18.4) è utile per calcolare \(P(E)\), se \(P(E \mid H_i)\) e \(P(H_i)\) sono facili da trovare. Quale esempio, consideriamo il seguente problema. Abbiamo tre urne, ciascuna delle quali contiene 100 palline:
Urna 1: 75 palline rosse e 25 palline blu,
Urna 2: 60 palline rosse e 40 palline blu,
Urna 3: 45 palline rosse e 55 palline blu.
Una pallina viene estratta a caso da un’urna anch’essa scelta a caso. Qual è la probabilità che la pallina estratta sia di colore rosso?
Sia \(R\) l’evento “la pallina estratta è rossa” e sia \(U_i\) l’evento che corrisponde alla scelta dell’\(i\)-esima urna. Sappiamo che
Gli eventi \(U_1\), \(U_2\) e \(U_3\) costituiscono una partizione dello spazio campione in quanto \(U_1\), \(U_2\) e \(U_3\) sono eventi mutualmente esclusivi ed esaustivi, ovvero \(P(U_1 \cup U_2 \cup U_3) = 1.0\). In base al teorema della probabilità totale, la probabilità di estrarre una pallina rossa è dunque
18.5. L’indipendendenza stocastica#
Un concetto fondamentale per l’applicazione della probabilità in campo statistico è l’indipendenza stocastica. L’equazione (18.1) offre un modo intuitivo per esprimere l’indipendenza tra due eventi \(A\) e \(B\): se \(A\) e \(B\) sono indipendenti, il verificarsi di \(A\) non influisce sulla probabilità del verificarsi di \(B\), e viceversa. In altre parole, il verificarsi di uno dei due eventi non condiziona la probabilità dell’altro evento. Infatti, per l’eq. (18.1), si ha che, se \(A\) e \(B\) sono due eventi indipendenti, risulta:
Possiamo dunque dire che due eventi \(A\) e \(B\) sono indipendenti se
Tre eventi, \(A\), \(B\) e \(C\) sono indipendenti se venongno soddisfatte le seguenti condizioni:
Se solo le prime tre condizioni vengono soddisfatte, allora gli eventi si dicono indipendenti a due a due.
Consideriamo il seguente problema. Nel lancio di due dadi non truccati, si considerino gli eventi: \(A\) = “esce un 1 o un 2 nel primo lancio” e \(B\) = “il punteggio totale è 8”. Gli eventi \(A\) e \(B\) sono indipendenti?
Calcoliamo \(P(A)\):
r = range(1, 7)
sample = [(i, j) for i in r for j in r]
A = [roll for roll in sample if roll[0] == 1 or roll[0] == 2]
print(A)
print(f"{len(A)} / {len(sample)}")
[(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)]
12 / 36
Calcoliamo \(P(B)\):
B = [roll for roll in sample if roll[0] + roll[1] == 8]
print(B)
print(f"{len(B)} / {len(sample)}")
[(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)]
5 / 36
Calcoliamo \(P(A \cap B)\):
I = [
roll
for roll in sample
if (roll[0] == 1 or roll[0] == 2) and (roll[0] + roll[1] == 8)
]
print(I)
print(f"{len(I)} / {len(sample)}")
[(2, 6)]
1 / 36
Gli eventi \(A\) e \(B\) non sono statisticamente indipendenti dato che \(P(A \cap B) \neq P(A)P(B)\):
12/36 * 5/36 == 1/36
False
18.6. Esercizio di ricapitolazione con Python#
Seguendo il metodo descritto nel libro “Think Bayes” di Downey [Dow21], utilizzeremo una definizione di probabilità semplice e intuitiva per facilitare la comprensione dei concetti fino ad ora descritti. In particolare, la nostra definizione di probabilità si adatta a esercizi che coinvolgono insiemi finiti, e considereremo la probabilità come la frazione di elementi che soddisfano un certo criterio rispetto al totale degli elementi dell’insieme. In altre parole, per calcolare la probabilità di un evento, conteremo quanti elementi dell’insieme rientrano in quell’evento e divideremo questo numero per il totale degli elementi dell’insieme. Questo rende più facile comprendere come funzionano i calcoli di probabilità e applicarli a situazioni pratiche.
Considereremo qui il dataset penguins inteso come un insieme finito sul quale definire vari eventi. Iniziamo ad importare i dati ed escludiamo i dati mancanti.
import pandas as pd
df = pd.read_csv('data/penguins.csv')
df.dropna(inplace=True)
df.info()
<class 'pandas.core.frame.DataFrame'>
Int64Index: 333 entries, 0 to 343
Data columns (total 8 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 species 333 non-null object
1 island 333 non-null object
2 bill_length_mm 333 non-null float64
3 bill_depth_mm 333 non-null float64
4 flipper_length_mm 333 non-null float64
5 body_mass_g 333 non-null float64
6 sex 333 non-null object
7 year 333 non-null int64
dtypes: float64(4), int64(1), object(3)
memory usage: 23.4+ KB
Ora, poniamoci la domanda se ciascun pinguino viva o meno sull’isola Dream. Per fare ciò, useremo una funzione che ci restituirà un oggetto Pandas Series contenente valori booleani. In particolare, ogni valore sarà True se il pinguino associato vive sull’isola Dream, altrimenti sarà False. In questo modo, avremo un elenco di valori che ci indicheranno per ciascun pinguino se vive o meno sull’isola Dream, utilizzando la potenza di Pandas per effettuare rapidamente questo tipo di calcoli.
on_dream = df['island'] == "Dream"
on_dream.head()
0 False
1 False
2 False
4 False
5 False
Name: island, dtype: bool
Essendo che il valore True corrisponde a 1 e il valore False corrisponde a 0, possiamo utilizzare la funzione .sum() per contare il numero di pinguini che vivono sull’isola Dream. In altre parole, sommando tutti i valori True nell’oggetto Pandas Series ottenuto prima, otterremo il numero totale di pinguini che vivono sull’isola Dream nel nostro campione di dati. Con questa operazione scopriamo che ci sono 123 pinguini che sono stati osservati sull’isola Dream.
on_dream.sum()
123
Per ottenere la proporzione di pinguini che vivono sull’isola Dream, dobbiamo calcolare la frequenza assoluta dei pinguini sull’isola Dream e dividere questo valore per il numero totale di pinguini del nostro campione di dati. Possiamo calcolare questo valore utilizzando il metodo .mean() applicato all’oggetto Pandas Series contenente i valori booleani True e False, ottenuto in precedenza. Questo metodo calcola la media aritmetica di tutti i valori nella serie, dove il valore True viene considerato come 1 e il valore False come 0. In questo modo, il risultato finale ci darà la proporzione di pinguini che vivono sull’isola Dream rispetto al totale dei pinguini del nostro campione di dati.
on_dream.mean()
0.36936936936936937
Circa il 36.9% di tutti i pinguini del nostro campione di dati vivono sull’isola Dream. Questo significa che, se scegliamo un pinguino a caso da questo insieme, la probabilità che viva sull’isola Dream è del 36.9%, ovvero 0.369.
Per automatizzare il calcolo della probabilità, possiamo inserire il codice precedente in una funzione. Questa funzione prenderà in input un oggetto Pandas Series contenente valori booleani, rappresentanti la presenza o meno di un certo attributo, e calcolerà la probabilità come la media aritmetica di tutti i valori nella serie, dove il valore True viene considerato come 1 e il valore False come 0. In questo modo, la funzione calcolerà la proporzione di True rispetto al totale dei valori nella serie e restituirà il valore corrispondente alla probabilità cercata.
def prob(A):
"""Computes the probability of a proposition, A."""
return A.mean()
Verifichiamo.
prob(on_dream)
0.36936936936936937
Troviamo ora la probabilità che un pinguino sia di genere femminile.
female = df["sex"] == "female"
prob(female)
0.4954954954954955
18.6.1. Intersezione di eventi (congiunzione)#
L’intersezione tra due insiemi corrisponde all’operazione logica della congiunzione. In altre parole, date due proposizioni \(p\) e \(q\), la loro congiunzione è vera solo se entrambe sono vere. Se abbiamo due oggetti Pandas Series contenenti valori booleani, possiamo utilizzare l’operatore & per trovare la loro congiunzione. Questo operatore restituisce un nuovo oggetto Series in cui i valori sono True solo se entrambi i corrispondenti valori nelle due serie sono True.
Definiamo ora un nuovo evento, chiamato “small”, che identifica i pinguini la cui massa corporea è inferiore al quantile di ordine 1/3. In altre parole, consideriamo la distribuzione dei pesi dei pinguini nel nostro campione di dati e identifichiamo i pinguini il cui peso è inferiore al valore corrispondente al quantile di ordine 1/3 della distribuzione. Questo evento è rappresentato da un oggetto Pandas Series booleano, in cui i valori sono True se il peso del pinguino è inferiore al quantile di ordine 1/3 e False altrimenti.
small = df["body_mass_g"] < df["body_mass_g"].quantile(1/3)
prob(small)
0.30930930930930933
Calcoliamo ora la probabilità che un pinguino sia di sesso femminile e, allo stesso tempo, appartenga alla categoria “small”. In altre parole, vogliamo calcolare la probabilità che si verifichino contemporaneamente due eventi: che un pinguino sia di sesso femminile e che appartenga alla categoria “small”.
prob(female & small)
0.2552552552552553
Come ci possiamo aspettare la probabilità dell’intersezione è minore della probabilità di “small” dato che non tutti i pinguini più piccoli sono di genere femminile.
18.6.2. Probabilità condizionata#
Come abbiamo visto in precedenza, la probabilità condizionata è la probabilità calcolata su un sottoinsieme di eventi. Per selezionare un sottoinsieme di dati in un oggetto Pandas, utilizziamo la notazione delle parentesi quadre. Nell’istruzione seguente, selezioniamo solo i pinguini di sesso femminile tra quelli che appartengono alla categoria “small”, ovvero quelli il cui peso corporeo è inferiore al quantile di ordine 1/3.
selected = female[small]
prob(selected)
0.8252427184466019
È importante notare la sintassi utilizzata in questo passaggio: quando inseriamo un oggetto Series booleano (in questo caso chiamato small) tra le parentesi quadre che seguono un oggetto Series (in questo caso chiamato female), stiamo selezionando solo le righe di female per le quali small ha il valore True.
Definiamo ora una funzione che prende in input due oggetti Series booleani, proposition e given, e restituisce la probabilità condizionata di proposition rispetto a given. In altre parole, la funzione calcola la probabilità che proposition si verifichi, sapendo che given si è verificato.
def conditional(proposition, given):
return prob(proposition[given])
Calcoliamo ora la probabilità condizionata che un pinguino sia di sesso femminile, dato che appartiene alla categoria “small”, ovvero il sottoinsieme di pinguini il cui peso corporeo è inferiore al quantile di ordine 1/3.
conditional(female, given=small)
0.8252427184466019
Troviamo ora la probabilità di essere di genere femminile, se consideriamo solo i pinguini sull’isola Dream, \(P(\text{female} \mid \text{Dream})\).
conditional(female, given=on_dream)
0.4959349593495935
Lo stesso risultato si ottiene applicando la definizione di probabilità condizionata.
prob(female & on_dream) / prob(on_dream)
0.49593495934959353
Calcoliamo la probabilità di estrarre a caso un pinguino di sesso femminile che vive sull’isola Dream.
prob(female & on_dream)
0.1831831831831832
Possiamo ottenere lo stesso risultato del calcolo precedente, ovvero la probabilità di estrarre a caso un pinguino di sesso femminile che vive sull’isola Dream, usando la probabilità condizionata per calcolare l’intersezione tra i due eventi.
conditional(female, given=on_dream) * prob(on_dream)
0.18318318318318316
18.7. Commenti e considerazioni finali#
La probabilità condizionata riveste un ruolo fondamentale poiché ci permette di definire in modo preciso il concetto di indipendenza statistica. Uno degli aspetti cruciali dell’analisi statistica riguarda la valutazione dell’associazione tra due variabili. Nel presente capitolo abbiamo esaminato il concetto di indipendenza, inteso come contrario all’associazione, mentre in seguito esploreremo come effettuare inferenze sulla correlazione tra variabili.
