19. Il teorema di Bayes#
Il teorema di Bayes è un importante risultato della teoria delle probabilità che ci consente di calcolare le probabilità a posteriori di eventi ipotetici, date le loro probabilità a priori e una nuova informazione. In altre parole, ci permette di aggiornare le nostre conoscenze in modo razionale alla luce di nuove evidenze.
In questo contesto, supponiamo di avere una partizione dell’evento certo \(\Omega\) in due soli eventi mutuamente esclusivi, che chiamiamo ipotesi \(H_1\) e \(H_2\). Supponiamo inoltre di conoscere le probabilità a priori \(P(H_1)\) e \(P(H_2)\) delle due ipotesi. Consideriamo ora un terzo evento \(E\), con probabilità non nulla, di cui conosciamo le probabilità condizionate \(P(E \mid H_1)\) e \(P(E \mid H_2)\), ovvero la probabilità che si verifichi l’evento \(E\) dati i valori delle due ipotesi. Supponendo che si sia verificato l’evento \(E\), vogliamo conoscere le probabilità a posteriori delle ipotesi, ovvero \(P(H_1 \mid E)\) e \(P(H_2 \mid E)\).
La figura seguente rappresenta una partizione dell’evento certo in due eventi chiamati ‘ipotesi’ \(H_1\) e \(H_2\). L’evidenza \(E\) è un sottoinsieme dello spazio campione.
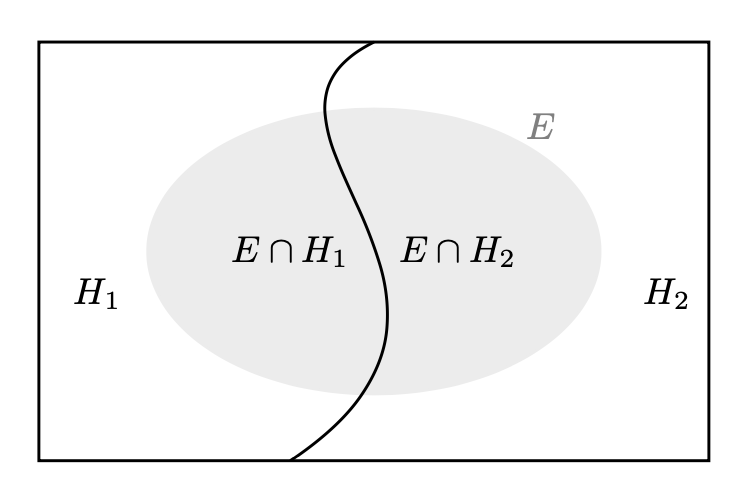
Per trovare la probabilità dell’ipotesi 1 data l’evidenza osservata, scriviamo:
Possiamo sostituire \(P(E \cap H_1)\) con \(P(E \mid H_1)P(H_1)\) data la definizione di probabilità condizionata \(P(E \mid H_1) = \frac{P(E \cap H_1)}{P(H_1)}\). Così facendo l’equazione precedente diventa:
Poiché \(H_1\) e \(H_2\) sono eventi disgiunti, la probabilità dell’evento \(E\) può essere calcolata utilizzando il teorema della probabilità totale:
Sostituendo questi risultati nella formula di Bayes, otteniamo:
L’eq. (19.1) è il caso più semplice della formula di Bayes, dove ci sono solo due eventi disgiunti \(H_1\) e \(H_2\). Il caso generale può essere formulato nel modo seguente.
Teorema
Sia \((H_i)_{i\geq 1}\) una partizione dell’evento certo \(\Omega\) e sia \(E \subseteq \Omega\) un evento tale che \(P(E) > 0\), allora, per \(i = 1, \dots, \infty\):
Il teorema di Bayes è molto utile perché ci permette di aggiornare le nostre credenze sulla base di nuove informazioni. In particolare, ci dice come trasformare le probabilità a priori in probabilità a posteriori, una volta che abbiamo osservato un nuovo evento. Questo teorema è utilizzato in molti campi, tra cui l’intelligenza artificiale, la statistica, la biologia, la psicologia e molti altri.
19.1. Interpretazione#
Possiamo identificare tre concetti fondamentali nell’eq. (19.2). I primi due distinguono la misura di fiducia che si ha precedentemente al verificarsi dell’evidenza \(E\) rispetto a quella che si ha successivamente al verificarsi dell’evidenza \(E\). Pertanto, considerando gli eventi \(H, E \subseteq \Omega\):
La probabilità a priori, \(P(H)\), rappresenta la probabilità assegnata all’ipotesi \(H\) prima di conoscere l’evidenza \(E\).
La probabilità a posteriori, \(P(H \mid E)\), rappresenta l’aggiornamento della probabilità a priori al verificarsi dell’evidenza \(E\).
Il terzo concetto definisce la probabilità dell’evidenza \(E\) quando l’ipotesi \(H\) è vera, ovvero la probabilità dell’evidenza in base all’ipotesi. Pertanto, dati gli eventi \(H\) e \(E\):
La verosimiglianza di \(E\) dato \(H\), \(P(E \mid H)\), rappresenta la probabilità condizionata dell’evidenza \(E\) data l’ipotesi \(H\).
Si osservi che per il calcolo del denominatore dell’eq. (19.2) si fa uso del teorema della probabilità totale.
Il teorema di Bayes è fondamentale nell’interpretazione soggettiva della probabilità perché ci permette di aggiornare la nostra credenza riguardo all’ipotesi \(H\) in base all’emergere dell’evidenza \(E\). In pratica, il teorema di Bayes ci fornisce un metodo per calcolare la probabilità assegnata all’ipotesi \(H\) sulla base delle informazioni fornite dall’evidenza \(E\). Questo processo di aggiornamento della nostra credenza è estremamente importante perché ci consente di adeguare la probabilità assegnata all’ipotesi in base alle nuove informazioni a nostra disposizione. In altre parole, il teorema di Bayes ci permette di considerare l’informazione come un’entità dinamica e di tenere conto di come questa influenza la nostra credenza.
19.2. Teorema di Bayes e problema sulla mammografia e cancro al seno#
Un lettore attento si sarà reso conto che, in precedenza, abbiamo già applicato il teorema di Bayes quando abbiamo risolto il problema sulla mammografia e cancro al seno. In quel caso, le due ipotesi erano “la malattia è presente”, che possiamo denotare con \(M^+\), e “la malattia è assente”, \(M^-\). L’evidenza \(E\) era costituita dal risultato positivo al test (denotiamo questo evento con \(T^+\)). Con questa notazione, possiamo scrivere l’eq. (19.1) nel modo seguente:
Inserendo i dati del problema nella formula precedente otteniamo
19.3. Teorema di Bayes e valore predittivo di un test di laboratorio#
L’esercizio precedente illustra un importante utilizzo del teorema di Bayes. Esso ci permette di calcolare la probabilità di malattia in caso di test positivo o di assenza di malattia in caso di test negativo. Per fare ciò, abbiamo bisogno di conoscere tre informazioni chiave: la prevalenza di una malattia, la sensibilità e la specificità del test utilizzato per la diagnosi.
In particolare, la prevalenza di una malattia è la sua frequenza nella popolazione. La sensibilità del test ci dice quale percentuale di soggetti malati viene identificata come tali dal test. La specificità del test ci dice quale percentuale di soggetti sani viene identificata come tali dal test.
Il teorema di Bayes ci permette di combinare queste informazioni per calcolare la probabilità di avere la malattia (o di non averla) sulla base del risultato del test. In questo modo, possiamo utilizzare il teorema di Bayes per prendere decisioni informate sulla diagnosi e sul trattamento delle malattie.

L’esercizio precedente ha mostrato un importante utilizzo del teorema di Bayes. In particolare, abbiamo visto come il teorema di Bayes ci permette di calcolare la probabilità di avere una malattia quando il test risulta positivo o la probabilità di non avere la malattia quando il test risulta negativo. Per fare ciò, abbiamo bisogno di tre informazioni: la prevalenza della malattia, la sensibilità e la specificità del test diagnostico. Ora esamineremo più in dettaglio l’applicazione del teorema di Bayes in questo contesto.
La sensibilità del test è definita come la probabilità che il test dia un risultato positivo dato che la malattia è presente: \(P(T^+ \mid M^+)\). Una sensibilità del 100% significa che il test è positivo in tutti i casi di malattia, una sensibilità del 90% significa che il test è positivo nel 90% dei casi di malattia, e così via.
La specificità del test è definita come la probabilità che il test dia un risultato negativo dato che la malattia è assente: \(P(T^- \mid M^-)\). Una specificità del 100% significa che il test è negativo in tutti i casi di assenza di malattia, una specificità del 90% significa che il test è negativo nel 90% dei casi di assenza di malattia, e così via.
La prevalenza della malattia è definita come la probabilità che la malattia sia presente: \(P^+\). Possiamo interpretare la prevalenza come la proporzione di individui malati nella popolazione in un dato istante. Ad esempio, una prevalenza del 5 per mille significa che il 5 per mille della popolazione è affetto dalla malattia.
La seguente tabella chiarisce la terminologia utilizzata:
\(T^+\) |
\(T^-\) |
|
|---|---|---|
\(M^+\) |
\(P(T^+ \cap M^+)\) (sensibilità) |
\(P(T^- \cap M^+)\) (1 - sensibilità) |
\(M^-\) |
\(P(T^+ \cap M^-)\) (1 - specificità ) |
\(P(T^- \cap M^-)\) (specificità) |
Nel caso dell’applicazione del teorema di Bayes alla diagnosi medica, abbiamo bisogno di conoscere la prevalenza della malattia (la proporzione di individui malati nella popolazione), la sensibilità del test (la probabilità che il test dia un risultato positivo quando la malattia è presente) e la specificità del test (la probabilità che il test dia un risultato negativo quando la malattia è assente). Usando queste informazioni, possiamo calcolare il valore predittivo del test positivo, cioè la probabilità che una persona sia effettivamente malata dato che il test è risultato positivo.
In modo simile, possiamo calcolare il valore predittivo del test negativo, cioè la probabilità che una persona non sia malata dato che il test è risultato negativo.
Svolgiamo ora un esercizio in Python in cui calcoliamo il valore predittivo del test positivo e il valore predittivo del test negativo con i dati dell’esempio sulla mammografia e cancro al seno.
def positive_predictive_value_of_diagnostic_test(sens, spec, prev):
return (sens * prev) / (sens * prev + (1 - spec) * (1 - prev))
def negative_predictive_value_of_diagnostic_test(sens, spec, prev):
return (spec * (1 - prev)) / (spec * (1 - prev) + (1 - sens) * prev)
sens = 0.9 # sensibilità
spec = 0.9 # specificità
prev = 0.01 # prevalenza
res_pos = positive_predictive_value_of_diagnostic_test(sens, spec, prev)
print(f"P(M+ | T+) = {round(res_pos, 3)}")
P(M+ | T+) = 0.083
res_neg = negative_predictive_value_of_diagnostic_test(sens, spec, prev)
print(f"P(M- | T-) = {round(res_neg, 3)}")
P(M- | T-) = 0.999
Per fare un altro esempio, consideriamo il test antigenico rapido per il virus SARS-COV-2, che viene eseguito tramite tampone nasale, naso-oro-faringeo o saliva. L’Istituto Superiore di Sanità ha pubblicato un documento il 5 novembre 2020, in cui si afferma che, attualmente, i dati disponibili sui vari test per questi parametri sono quelli dichiarati dal produttore: la sensibilità è compresa tra il 70-86%, mentre la specificità è tra il 95-97%.
Nella settimana dal 17 al 23 marzo 2023, in Italia, il numero di individui attualmente positivi è stimato essere 138599 (fonte: Il Sole 24 Ore). Questo corrisponde a una prevalenza di circa il 2 per mille, su una popolazione di circa 59 milioni.
prev = 138599 / 59000000
prev
0.002349135593220339
Il nostro obiettivo è calcolare la probabilità di essere affetti da Covid-19, sapendo che il risultato del test (tampone rapido) è positivo, ovvero \(P(M^+ \mid T^+)\). Per farlo, useremo la formula del valore predittivo del test positivo:
sens = (0.7 + 0.86) / 2 # sensibilità
spec = (0.95 + 0.97) / 2 # specificità
res_pos = positive_predictive_value_of_diagnostic_test(sens, spec, prev)
print(f"P(M+ | T+) = {round(res_pos, 3)}")
P(M+ | T+) = 0.044
Pertanto, se il risultato del tampone è positivo, la probabilità di essere effettivamente affetti da Covid-19 è solo del 4.4%, approssimativamente.
Se la prevalenza fosse 100 volte superiore (cioè, pari al 23.5%), la probabilità di avere il Covid-19, dato un risultato positivo del tampone, aumenterebbe notevolmente e sarebbe pari all’85.7%, approssimativamente.
prev = 138599 / 59000000 * 100
res_pos = positive_predictive_value_of_diagnostic_test(sens, spec, prev)
print(f"P(M+ | T+) = {round(res_pos, 3)}")
P(M+ | T+) = 0.857
Se il risultato del test fosse negativo, considerando la prevalenza stimata del Covid-19 nella settimana dal 17 al 23 marzo 2023, la probabilità di non essere infetto sarebbe del 99.9%, approssimativamente.
sens = (0.7 + 0.86) / 2 # sensibilità
spec = (0.95 + 0.97) / 2 # specificità
prev = 138599 / 59000000 # prevalenza
res_neg = negative_predictive_value_of_diagnostic_test(sens, spec, prev)
print(f"P(M- | T-) = {round(res_neg, 3)}")
P(M- | T-) = 0.999
19.4. Aggiornamento bayesiano#
Il teorema di Bayes ci dice che la probabilità non è un fatto oggettivo, ma una valutazione soggettiva e condizionata. Nell’equazione del teorema di Bayes, ci sono due elementi nel numeratore: \(P(H_i)\) e \(P(E \mid H_i)\). La probabilità a priori \(P(H_i)\) rappresenta la conoscenza dell’agente sull’ipotesi \(H_i\), ovvero quanto l’agente confida in \(H_i\) prima di conoscere l’evidenza \(E\). Per calcolare la nuova probabilità che l’agente assegna all’ipotesi \(H_i\) alla luce dell’evidenza \(E\), chiamata probabilità a posteriori \(P(H_i \mid E)\), l’agente utilizza sia la probabilità a priori che la verosimiglianza \(P(E \mid H_i)\).
È importante notare che la probabilità a posteriori dipende sia dall’evidenza \(E\) che dalla conoscenza a priori dell’agente \(P(H_i)\). Ciò significa che non esiste una probabilità oggettiva. La probabilità a priori è un giudizio personale dell’agente e non ci sono criteri esterni per determinare se questo giudizio sia corretto o meno. Pertanto, ogni probabilità deve essere considerata come una rappresentazione del grado di fiducia soggettiva dell’agente.
Poiché ogni assegnazione probabilistica rappresenta uno stato di conoscenza che è arbitrario, non è necessario che gli agenti abbiano lo stesso accordo. Tuttavia, la teoria delle probabilità fornisce uno strumento che consente di aggiornare in modo razionale il grado di fiducia che attribuiamo a un’ipotesi alla luce di nuove evidenze. Questo processo di aggiornamento del grado di fiducia è noto come aggiornamento bayesiano. In questo modo, l’agente può sempre formulare un’ipotesi a posteriori che può essere aggiornata sulla base delle nuove evidenze disponibili.
19.5. Esercizio di ricapitolazione con Python#
Proseguendo con l’esempio del capitolo precedente, usiamo i dati penguins per applicare il teorema di Bayes.
import pandas as pd
df = pd.read_csv('data/penguins.csv')
df.dropna(inplace=True)
df.info()
<class 'pandas.core.frame.DataFrame'>
Int64Index: 333 entries, 0 to 343
Data columns (total 8 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 species 333 non-null object
1 island 333 non-null object
2 bill_length_mm 333 non-null float64
3 bill_depth_mm 333 non-null float64
4 flipper_length_mm 333 non-null float64
5 body_mass_g 333 non-null float64
6 sex 333 non-null object
7 year 333 non-null int64
dtypes: float64(4), int64(1), object(3)
memory usage: 23.4+ KB
Riprendiamo le funzioni prob e conditional che abbiamo definito in precedenza.
def prob(A):
"""Computes the probability of a proposition, A."""
return A.mean()
def conditional(proposition, given):
return prob(proposition[given])
Per la congiunzione vale la proprietà di commutatività:
female = df["sex"] == "female"
small = df["body_mass_g"] < df["body_mass_g"].quantile(1/3)
prob(female & small) == prob(small & female)
True
Quindi possiamo scrivere:
conditional(female, given=small) * prob(small)
0.2552552552552553
oppure
conditional(small, given=female) * prob(female)
0.2552552552552552
Giungiamo così al teorema di Bayes:
conditional(female, given=small)
0.8252427184466019
conditional(small, given=female) * prob(female) / prob(small)
0.8252427184466018
oppure
conditional(small, given=female)
0.5151515151515151
conditional(female, given=small) * prob(small) / prob(female)
0.5151515151515152
19.6. Il problema delle due urne#
Supponiamo che vi siano due urne.
L’urna 1 (\(U_1\)) contiene 30 palline bianche (B) e 10 palline nere (N).
L’urna 2 (\(U_2\)) contiene 20 palline bianche e 20 palline nere.
Supponiamo di scegliere una delle urne a caso e, senza guardare, di scegliere una pallina a caso. Se la pallina è bianca, qual è la probabilità che provenga dall’urna 1?
Quello che vogliamo è la probabilità condizionata che abbiamo scelto dall’Urna 1 dato che abbiamo ottenuto una pallina bianca, \(P(U_1 \mid B)\).
Il problema ci fornisce le seguenti informazioni:
\(P(B \mid U_1)\) = 3/4,
\(P(B \mid U_2)\) = 1/2.
Il teorema di Bayes ci dice come le informazioni a disposizione si possono mettere in relazione con la domanda del problema:
Per calcolare la probabilità \(P(B)\) usiamo il teorema della probabilità totale:
ovvero
Concludiamo applicando il teorema di Bayes:
Il processo di aggiornamento bayesiano può essere anche svolto nel modo seguente. Riscrivo il teorema di Bayes nel modo seguente:
La probabilità \(P(H)\) è la probabilità delle ipotesi prima di avere osservato i dati. Nel nostro caso, le due ipotesi sono “Urna 1” e “Urna 2”, entrambe con la stessa probabilità, dato che non abbiamo ragioni a priori per dare più peso ad un’ipotesi rispetto all’altra. Costruiamo una tabella con un DataFrame in cui inseriamo la colonna prior:
table = pd.DataFrame(index=['Urn 1', 'Urn 2'])
table['prior'] = 1/2, 1/2
table
| prior | |
|---|---|
| Urn 1 | 0.5 |
| Urn 2 | 0.5 |
La probabilità \(P(D \mid H)\) è la probabilità dei dati, data l’ipotesi. È chiamata verosimiglianza. La probabilità di una pallina bianca dato che viene estratta dall’Urna 1 è 3/4. La probabilità di una pallina bianca dato che viene estratta dall’Urna 1 è 1/2. Aggiungo alla tabella la colonna likelihood.
table['likelihood'] = 3/4, 1/2
table
| prior | likelihood | |
|---|---|---|
| Urn 1 | 0.5 | 0.75 |
| Urn 2 | 0.5 | 0.50 |
La probabilità \(P(H \mid D)\) è la probabilità dell’ipotesi dopo avere osservato i dati. Si ottiene come il prodotto della verosimiglianza per la probabilità a priori, diviso per una costante di normalizzazione. Iniziamo a calcolare il la distribuzione a posteriori non normalizzata.
table['unnorm'] = table['prior'] * table['likelihood']
table
| prior | likelihood | unnorm | |
|---|---|---|---|
| Urn 1 | 0.5 | 0.75 | 0.375 |
| Urn 2 | 0.5 | 0.50 | 0.250 |
La probabilità dei dati, \(P(D)\), ovvero il numeratore bayesiano, è dato dalla somma di tutti i valori della distribuzione a posteriori non normalizzata:
prob_data = table['unnorm'].sum()
Possiamo ora normalizzare la distribuzione a posteriori:
table['posterior'] = table['unnorm'] / prob_data
table
| prior | likelihood | unnorm | posterior | |
|---|---|---|---|---|
| Urn 1 | 0.5 | 0.75 | 0.375 | 0.6 |
| Urn 2 | 0.5 | 0.50 | 0.250 | 0.4 |
19.7. Il problema dei dadi#
Il metodo precedente può anche essere usato quando ci sono più di due ipotesi. Downey [Dow21] discute il seguente problema. Supponiamo che nell’Urna 1 ci sia un dado a 6 facce, nell’Urna 2 un dado a 8 facce e nell’Urna 3 un dado a 12 facce. Un dado viene estratto a caso da un’urna e produce il risultato 1. Qual è la probabilità che ho usato un dado a 6 facce?
Inizio a definire le tre ipotesi.
table2 = pd.DataFrame(index=[6, 8, 12])
table2
| 6 |
|---|
| 8 |
| 12 |
Per evitare arrotondamenti uso la funzione Fraction(). Inizio a definire la distribuzione a priori.
from fractions import Fraction
table2['prior'] = Fraction(1, 3)
table2
| prior | |
|---|---|
| 6 | 1/3 |
| 8 | 1/3 |
| 12 | 1/3 |
Definisco la verosimiglianza. Se il dado è a 6 facce, la probabilità di ottenere 1 è 1/6; se il dado ha 8 facce è 1/8; se il dado ha 12 facce è 1/12.
table2['likelihood'] = Fraction(1, 6), Fraction(1, 8), Fraction(1, 12)
table2
| prior | likelihood | |
|---|---|---|
| 6 | 1/3 | 1/6 |
| 8 | 1/3 | 1/8 |
| 12 | 1/3 | 1/12 |
Trovo la distribuzione a posteriori non normalizzata.
table2['unnorm'] = table2['prior'] * table2['likelihood']
table2
| prior | likelihood | unnorm | |
|---|---|---|---|
| 6 | 1/3 | 1/6 | 1/18 |
| 8 | 1/3 | 1/8 | 1/24 |
| 12 | 1/3 | 1/12 | 1/36 |
Normalizzo.
prob_data = table2['unnorm'].sum()
table2['posterior'] = table2['unnorm'] / prob_data
table2
| prior | likelihood | unnorm | posterior | |
|---|---|---|---|---|
| 6 | 1/3 | 1/6 | 1/18 | 4/9 |
| 8 | 1/3 | 1/8 | 1/24 | 1/3 |
| 12 | 1/3 | 1/12 | 1/36 | 2/9 |
La probabilità posteriore del dado a 6 facce è 4/9, che è più grande delle probabilità degli altri dadi, 3/9 e 2/9. Intuitivamente, il dado a 6 facce è il più probabile perché ha la probabilità più grande di produrre il risultato che abbiamo osservato.
19.8. Commenti e considerazioni finali#
La riflessione epistemologica moderna ha dimostrato che la conoscenza non può essere considerata come certezza o garanzia razionale della verità, ma come decisioni prese in condizioni di incertezza. La logica deduttiva, che si basa sulle forme della dimostrazione matematica, non è sufficiente per il ragionamento scientifico, poiché la ricerca scientifica richiede una “logica dell’incertezza”, fornita dalla teoria delle probabilità e in particolare dal teorema di Bayes. Questo teorema è importante per la rivoluzione metodologica contemporanea che cerca di risolvere la crisi della replicabilità dei risultati della ricerca [Ioa05], che sta affliggendo molti campi, tra cui la psicologia. Il libro “Bernoulli’s Fallacy” di Clayton [Cla21] approfondisce questo tema.
In questo capitolo, abbiamo presentato il teorema di Bayes utilizzando variabili casuali discrete, che sono il caso più controintuitivo. È invece più intuitivo applicare il teorema di Bayes alle variabili casuali continue, che verranno trattate nel capitolo successivo. Puoi trovare maggiori informazioni sul teorema di Bayes applicato alle variabili casuali continue nel notebook Credibilità, modelli e parametri.
19.9. Watermark#
%load_ext watermark
%watermark -n -u -v -iv -w
Last updated: Sat Jun 17 2023
Python implementation: CPython
Python version : 3.11.3
IPython version : 8.12.0
pandas: 1.5.3
Watermark: 2.3.1
