Codice
| 0.50 | 0.50 | 0.00 | 0.00 | 0.00 | 0.00 |
| 0.25 | 0.50 | 0.25 | 0.00 | 0.00 | 0.00 |
| 0.00 | 0.25 | 0.50 | 0.25 | 0.00 | 0.00 |
| 0.00 | 0.00 | 0.25 | 0.50 | 0.25 | 0.00 |
| 0.00 | 0.00 | 0.00 | 0.25 | 0.50 | 0.25 |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.50 | 0.50 |
Per introdurre il concetto di catena di Markov, supponiamo che una persona esegua una passeggiata casuale sulla retta dei numeri naturali considerando solo i valori 1, 2, 3, 4, 5, 6.1 Se la persona è collocata su un valore interno dei valori possibili (ovvero, 2, 3, 4 o 5), nel passo successivo è altrettanto probabile che rimanga su quel numero o si sposti su un numero adiacente. Se si muove, è ugualmente probabile che si muova a sinistra o a destra. Se la persona si trova su uno dei valori estremi (ovvero, 1 o 6), nel passo successivo è altrettanto probabile che rimanga rimanga su quel numero o si sposti nella posizione adiacente.
Questo è un esempio di una catena di Markov discreta. Una catena di Markov descrive il movimento probabilistico tra un numero di stati. Nell’esempio ci sono sei possibili stati, da 1 a 6, i quali corrispondono alle possibili posizioni della passeggiata casuale. Data la sua posizione corrente, la persona si sposterà nelle altre posizioni possibili con delle specifiche probabilità. La probabilità che si sposti in un’altra posizione dipende solo dalla sua posizione attuale e non dalle posizioni visitate in precedenza.
È possibile descrivere il movimento tra gli stati nei termini delle cosiddette probabilità di transizione, ovvero le probabilità di movimento tra tutti i possibili stati in un unico passaggio di una catena di Markov. Le probabilità di transizione sono riassunte in una matrice di transizione \(P\):
| 0.50 | 0.50 | 0.00 | 0.00 | 0.00 | 0.00 |
| 0.25 | 0.50 | 0.25 | 0.00 | 0.00 | 0.00 |
| 0.00 | 0.25 | 0.50 | 0.25 | 0.00 | 0.00 |
| 0.00 | 0.00 | 0.25 | 0.50 | 0.25 | 0.00 |
| 0.00 | 0.00 | 0.00 | 0.25 | 0.50 | 0.25 |
| 0.00 | 0.00 | 0.00 | 0.00 | 0.50 | 0.50 |
La prima riga della matrice di transizione \(P\) fornisce le probabilità di passare a ciascuno degli stati da 1 a 6 in un unico passaggio a partire dalla posizione 1; la seconda riga fornisce le probabilità di transizione in un unico passaggio dalla posizione 2 e così via. Per esempio, il valore \(P[1, 1]\) ci dice che, se la persona è nello stato 1, avrà una probabilità di 0.5 di rimanere in quello stato; \(P[1, 2]\) ci dice che c’è una probabilità di 0.5 di passare dallo stato 1 allo stato 2. Gli altri elementi della prima riga sono 0 perché, in un unico passaggio, non è possibile passare dallo stato 1 agli stati 3, 4, 5 e 6. Il valore \(P[2, 1]\) ci dice che, se la persona è nello stato 1 (seconda riga), avrà una probabilità di 0.25 di passare allo stato 1; avra una probabilità di 0.5 di rimanere in quello stato, \(P[2, 2]\); e avrà una probabilità di 0.25 di passare allo stato 3, \(P[2, 3]\); eccetera.
Si notino alcune importanti proprietà di questa particolare catena di Markov.
Un’importante proprietà di una catena di Markov irriducibile e aperiodica è che il passaggio ad uno stato del sistema dipende unicamente dallo stato immediatamente precedente e non dal come si è giunti a tale stato (dalla storia). Per questo motivo si dice che un processo markoviano è senza memoria. Tale “assenza di memoria” può essere interpretata come la proprietà mediante cui è possibile ottenere un insieme di campioni casuali da una distribuzione di interesse. Nel caso dell’inferenza bayesiana, la distribuzione di interesse è la distribuzione a posteriori, \(p(\theta \mid y)\). Le catene di Markov consentono di stimare i valori di aspettazione di variabili rispetto alla distribuzione a posteriori.
La matrice di transizione che si ottiene dopo un enorme numero di passi di una passeggiata casuale markoviana si chiama distribuzione stazionaria. Se una catena di Markov è irriducibile e aperiodica, allora ha un’unica distribuzione stazionaria \(w\). La distribuzione limite di una tale catena di Markov, quando il numero di passi tende all’infinito, è uguale alla distribuzione stazionaria \(w\).
Un metodo per dimostrare l’esistenza della distribuzione stazionaria di una catena di Markov è quello di eseguire un esperimento di simulazione. Iniziamo una passeggiata casuale partendo da un particolare stato, diciamo la posizione 3, e quindi simuliamo molti passaggi della catena di Markov usando la matrice di transizione \(P\). Al crescere del numero di passi della catena, le frequenze relative che descrivono il passaggio a ciascuno dei sei possibili nodi della catena approssimano sempre meglio la distribuzione stazionaria \(w\).
Senza entrare nei dettagli della simulazione, la Figura E.1 mostra i risultati ottenuti in 10,000 passi di una passeggiata casuale markoviana. Si noti che, all’aumentare del numero di iterazioni, le frequenze relative approssimano sempre meglio le probabilità nella distribuzione stazionaria \(w = (0.1, 0.2, 0.2, 0.2, 0.2, 0.1)\).
set.seed(123)
s <- vector("numeric", 10000)
s[1] <- 3
for (j in 2:10000) {
s[j] <- sample(1:6, size = 1, prob = P[s[j - 1], ])
}
S <- data.frame(
Iterazione = 1:10000,
Location = s
)
S %>%
mutate(
L1 = (Location == 1),
L2 = (Location == 2),
L3 = (Location == 3),
L4 = (Location == 4),
L5 = (Location == 5),
L6 = (Location == 6)
) %>%
mutate(
Proporzione_1 = cumsum(L1) / Iterazione,
Proporzione_2 = cumsum(L2) / Iterazione,
Proporzione_3 = cumsum(L3) / Iterazione,
Proporzione_4 = cumsum(L4) / Iterazione,
Proporzione_5 = cumsum(L5) / Iterazione,
Proporzione_6 = cumsum(L6) / Iterazione
) %>%
dplyr::select(
Iterazione, Proporzione_1, Proporzione_2, Proporzione_3,
Proporzione_4, Proporzione_5, Proporzione_6
) -> S1
gather(S1, Outcome, Probability, -Iterazione) -> S2
ggplot(S2, aes(Iterazione, Probability)) +
geom_line() +
facet_wrap(~Outcome, ncol = 3) +
ylim(0, .4) +
ylab("Frequenza relativa") +
# theme(text=element_text(size=14)) +
scale_x_continuous(breaks = c(0, 3000, 6000, 9000))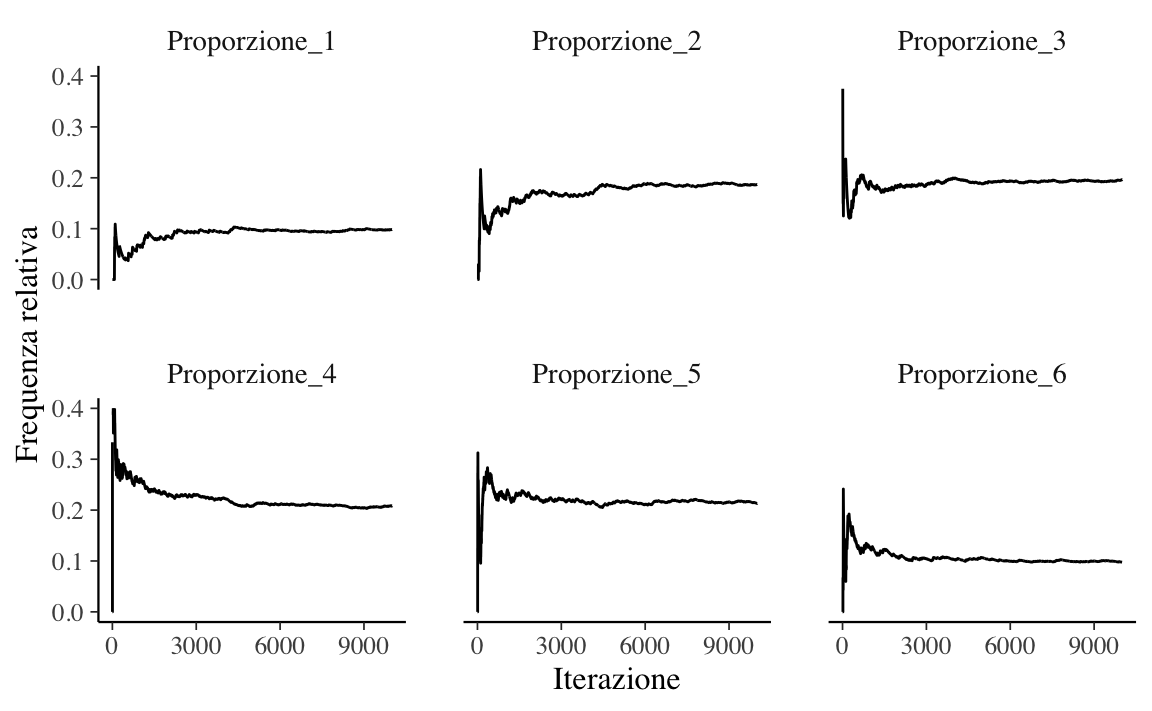
Il metodo di campionamento utilizzato dagli algoritmi MCMC consente di creare una catena di Markov irriducibile e aperiodica, la cui distribuzione stazionaria equivale alla distribuzione a posteriori \(p(\theta \mid y)\).
Seguiamo qui la presentazione fornita da Bob Carpenter.↩︎